基于多种群遗传算法与Plant Simulation的车间调度优化

代礼奇，彭 可，崔 焱，刘 明

（湖南师范大学 工程与设计学院，湖南 长沙 410081）

1 引言

随着硬质合金在现代工业中的广泛应用，对其混合料的质量要求也越来越高。该生产线引进的湿磨-喷雾干燥生产工艺满足该质量要求，但其设备多且复杂，按经验进行生产排产效率低下。因而需要一种科学的排产方法对该类多工序、多设备的生产线进行合理排产。

硬质合金混合料生产线调度问题作为典型的混合流水车间调度问题（HFSP），当其工件种类、工序、设备数较少时，可用分支定界和线性规划等精确方法求出最优解；而当其生产规模扩大时，解空间会呈爆炸式增长，精确求解方法很难在合理的时间内求出最优解。而以遗传算法、模拟退火算法、禁忌搜索算法等为代表的启发式算法，以其能在合理的计算时间内求出高质量的解的特点而被广泛应用于求解HFSP问题。轩华等改变初始种群、交叉概率和变异概率提出一种防止陷入局部最优的自适应混合遗传算法求解带机器阻塞约束的HFSP问题。耿凯峰等改进编码方式、交叉和变异算子提出一种改进Memtic算法用于求解带工序跳跃的绿色混合流水车间。孟磊磊等提出一种改进的回溯搜索算法求解带阻塞约束的不相关并行机HFSP问题。郑旭[设计两种不同编码方式的蚁群优化算法求解考虑阻塞时间和工件差异约束的HFSP问题。袁庆欣等分别采用NSGA-Ⅱ、NSGA-Ⅲ算法求解考虑有限缓冲区约束的HFSP问题。现有文献的研究，对传统启发式算法的全局搜索能力进行了改善，且在传统HFSP问题中加入了与实际车间更贴合的约束条件。最后，基于算例对算法的有效性进行验证。

综上，目前关于生产调度优化的文献对优化后的方案仅在数值上进行了验证。本文基于上述研究思路，提出一种多种群遗传算法对该硬质合金生产线进行优化，并引入Plant Simulation生产线仿真平台对上述优化方案进行更实际地验证。

2 问题描述

HFSP问题可以描述为：n个工件在s（s≥2）道工序上连续加工，工序j含有m（m>0；j=1，2，…，s）台设备，生产线共有m台设备，且至少存在一个工序有多台设备。因而，HFSP问题通过改变工件加工顺序及各工件设备分配来优化。

2.1 车间加工情况描述

硬质合金混合料生产线包含配粉、球磨、干燥三道工序，各工序中分别包含4台、16台、4台设备，工序间通过AGV小车进行物料运输。对该生产线作业调度问题有如下描述：一批料24个工件分别要依次在3个工序上的一台设备上完成加工，各工序加工时间及工序间AGV路线已知。由于设备加工时间较长，同一批料出料时间相对比较集中，且同一工序的各设备加工时长因运输距离及设备型号等因素有明显差距。因此，调整三道工序中设备的使用顺序，可有效提高该生产线的生产效率。该生产线生产流程示意图如图1所示。并对其约束条件做出如下假设。

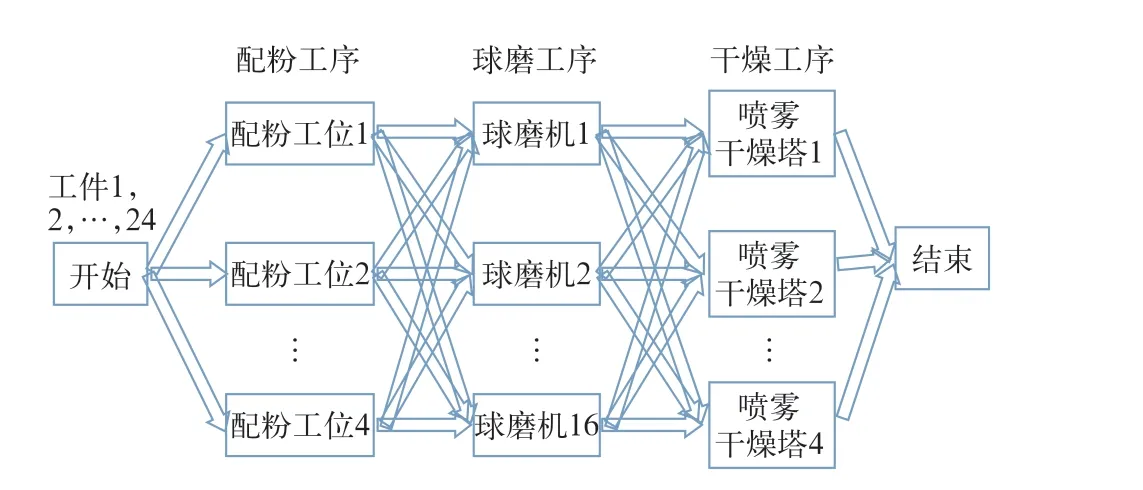
图1 硬质合金混合料生产线生产流程示意图

1）生产线各设备布局已确定，各设备间AGV的移动路线确定且唯一。

2）各工序间物料运输的AGV型号相同，且执行任务期间不能被其他任务打断。

3）每个工件都要固定加工要求依次完成所有工序，完成每个工序时在该工序内任一设备上完成即可。

4）每个工件都有固定的加工顺序，不能任意打乱加工顺序。

5）每台设备同一时刻只能处理一个工件。

6）加工工艺要求不同工件在同一设备上的加工时间相同。

7）为方便计算，各设备加工时长包括该设备加工基本时长、AGV送料运输时长、人工装卸料时长以及清洗搅拌等辅助工序时长。

2.2 调度问题建模

为方便后续描述，对以下参数进行符号定义。

i：各加工工件序号；I：工件集；n：工件总数；j：工序序号；s：工序数；J：工序序号；O：工件i的第j道工序；k：设备序号；m：设备总数；m：工序j的设备数；K：车间设备集；K：工序j的设备集；M：值为无穷大的实数；P：工件i在设备k上的加工时间；B：工件i在设备k上开始加工时间；E：工件i在设备k上加工完成时间。

优化目标函数为最小化最大加工完成时间为f=min（Emax）；约束条件为

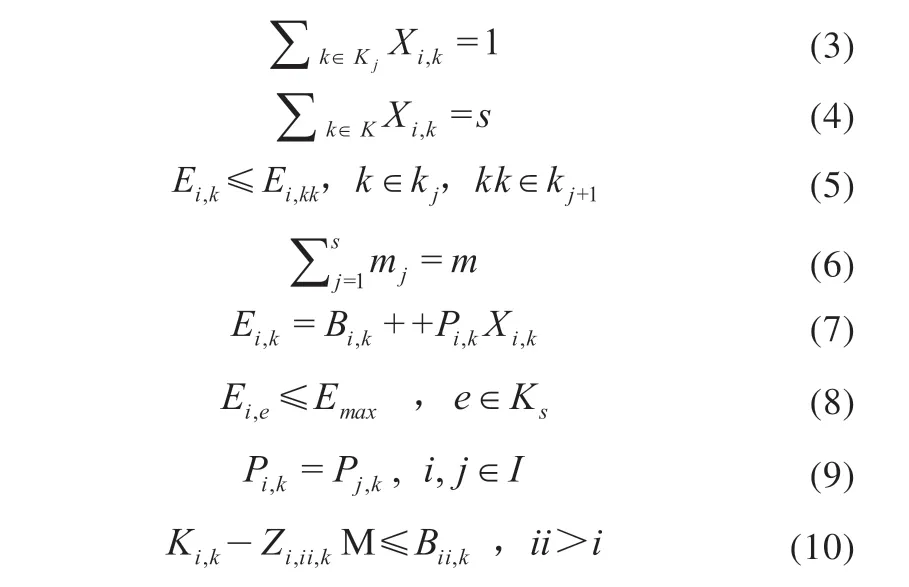
式(3)表示同一工件在同一工序某一台设备上加工即可；式(4)和式(5)表示每个工件都要依次完成s道工序；式(6)表示每个设备只能完成某一种工序；式(7)表示工件i在设备k上加工完成时间为开始加工时间与加工时间之和；式(8)表示最大完工时间应不小于任意工件的完工时间；式(9)表示不同工件在同一设备上的加工时间相同；式(10)表示考虑阻塞时设备k同一时刻只能处理一个工件。

3 算法设计

传统遗传算法的主要实现步骤为染色体编码、种群初始化、设置适应度函数、选择、交叉、变异等算子，重复选择、交叉、变异直至满足终止条件后输出结果。为改善遗传算法的搜索邻域，本文在传统遗传算法基础上提出一种引入精英种群、移民算子和人工选择算子的多种群遗传算法，各种群间采用不同交叉概率和变异概率进行协同进化。

3.1 染色体编码

遗传算法的染色体编码方式可以分为二进制编码、浮点编码、符号编码以及多参数级联编码等。本文以三道工序中的设备使用顺序为决策变量，各设备只能完成某一道工序。因此，本文采用多染色体实数编码，即每个个体有三条染色体，分别代表配粉工序、球磨工序、干燥工序的设备投产顺序。三道工序共24台设备，具体编码见表1。各工序编码顺序是按各设备在同工序设备中加工时间进行递增排列，即加工时长越小，编码号越小。

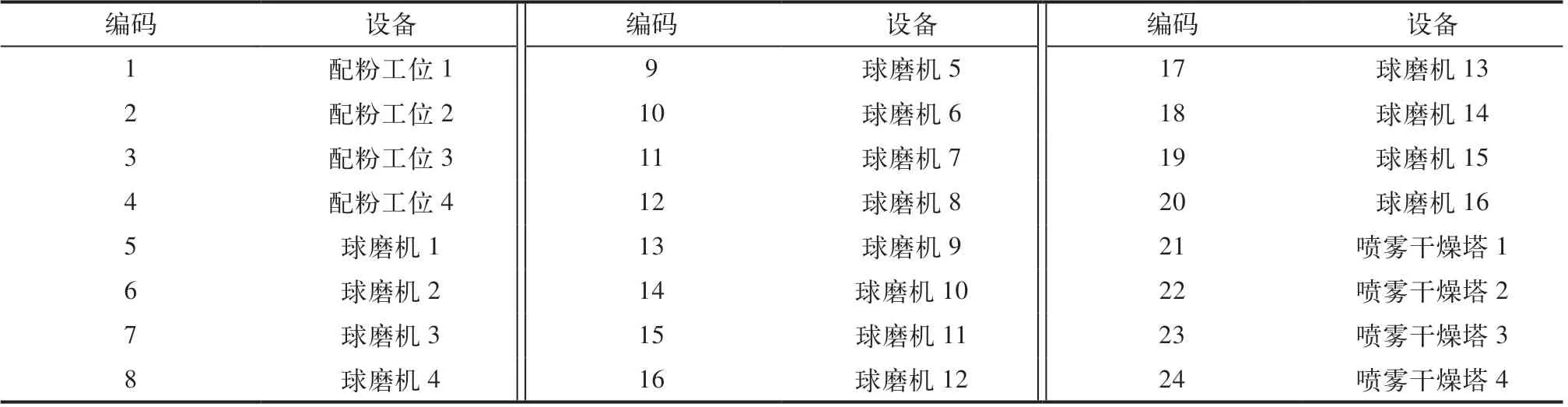
表1 三道工序编码

每个工件都要依次在配粉、球磨、干燥工序上任选一台设备上进行加工。默认经验排产是按加工时长优先排时长小的设备。实际生产按默认经验顺序进行排产，第一个工件加工设备依次为配粉工位1-球磨机1-喷雾干燥塔1，第二个工件加工设备依次为配粉工位2-球磨机2-喷雾干燥塔2，依次类推。以经验排产方案为例，该方案编码后对应的三条染色体分别为[1,2,3,4]，[5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20]，[21,22,23,24]。

3.2 种群初始化

初始化是遗传算法中的关键一步，初始种群的质量对遗传算法在整个搜索空间中的搜索速度与质量有着十分重要的关系。已有研究通常采用随机或其他单一初始化的方法，因而所得到的解的质量偏低。本文提出改进多种群遗传算法在产生初始种群时引入多个初始种群同时进行优化搜索，各初始种群间通过移民算子通信，从而实现多种群的协同进化，得到各种群进化的综合结果。

3.3 适应度函数

遗传算法中适应度函数是用来判别各基因遗传到下一代的概率。如何使适应度函数与求解对象有效匹配是检验遗传算法有效性的关键。本案例求解目的是一批工件总完成时间T的最小值，故以一批工件总完工时间T的倒数作为适应度函数。T的计算公式为

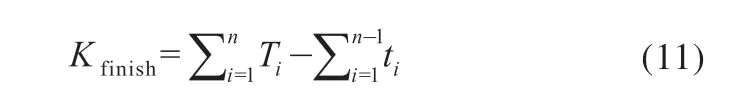
式中，n为一批工件包含的工件数；T表示加工完工件i所需要的时间；t表示在加工工件i时，工件i+1已完成任务所节省的时间。

适应度函数可以表示为

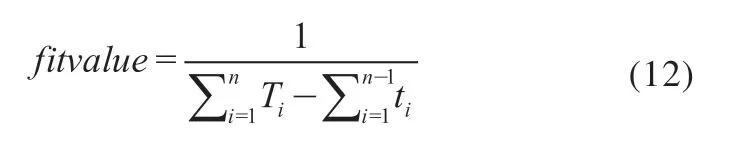
3.4 选择算子

选择算子是实现遗传思想“适者生存”的核心步骤，本文案例中选择算子采用轮盘赌选择。轮盘赌选择又称为比例选择方法，其基本思想是：各个个体被选中的概率与其适应度大小成正比，即适应度值越大的个体越容易被选中，对应到本文案例中一批工件总完工时间T越小的基因组越容易被选中。其具体操作过程为∑f

1）计算整个群体中每个个体的适应度，并将群里中所有个体的适应度累加求和得到适应度总和。

2）计算出群体中各个个体的相对适应度f/∑f，该相对适应度值即为该个体遗传到下一代群体的概率。

3.5 交叉算子

交叉运算为遗传算法中产生新个体的基本操作过程，指以一定的概率将一对父代基因的部分结构互相替换重组生成一对新的子代基因的操作。由于实数编码方式染色体上每个基因的唯一性，若采用简单交叉方式，会出现非法解。如一对父代染色体[1,2,3,4]，[2,3,4,1]，以单点交叉为例，交换后面两个基因，得到子代为[1,2,4,1]，[2,3,3,4]。两个子代中都有两个相同设备，与该染色体实际意义冲突。为避免染色体交叉产生非法解，本案例采用基于位置的交叉（Position-based Crossover，PBX）。其具体操作步骤为

1）随机选择一条父代染色体中的几个基因，选择的基因可不连续；

2）生成一条子代染色体，使该染色体与1）中所述父代染色体选中位置基因相同；

3）先找出1）中选中基因在另一条父代染色体上的位置，再将其余基因按顺序放入上一步生成的子代中得到一条子代染色体；

4）选择另一条父代染色体重复以上步骤得到第二条子代染色体。

以球磨工序的染色体为例，其交叉操作过程如图2所示。

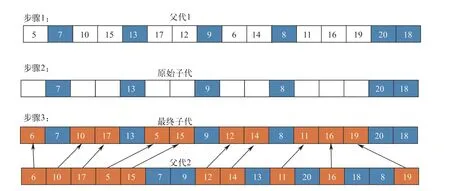
图2 PBX具体操作示意图

3.6 变异算子

在遗传算法中，变异算子的基本内容是指对群体P（t）中的每一个个体，以某一概率改变某一个或某一些基因座上的基因值为其他的等位基因。常用操作方法有均匀变异、边界变异、高斯变异、非均匀变异以及互联变异等。本文中案例采用互联变异方法，即先在父代染色体中随机选择两个基因，再交换其位置得到子代染色体。如父代染色体为[1,2,3,4]，随机选择基因2、4，得到新的子代染色体为[1,4,3,2]。

3.7 移民算子与人工选择算子

针对传统遗传算法容易过早收敛于局部邻域空间的现象。多种群遗传算法引入了移民算子和多个设有不同控制参数的初始种群，并定期通过移民算子将各种群中的最优个体替换掉其余某种群中的最差个体，在迭代遗传中实现种群间信息互换。

同时，多种群遗传算法引入人工选择算子和精华种群，在进化的每一代中通过人工选择算子将其他种群的最优个体添加到精华种群中，精华种群不用进行选择、交叉、变异等遗传操作，保证进化过程中各种群产生的最优个体不被破坏。其操作过程示意图如图3所示。

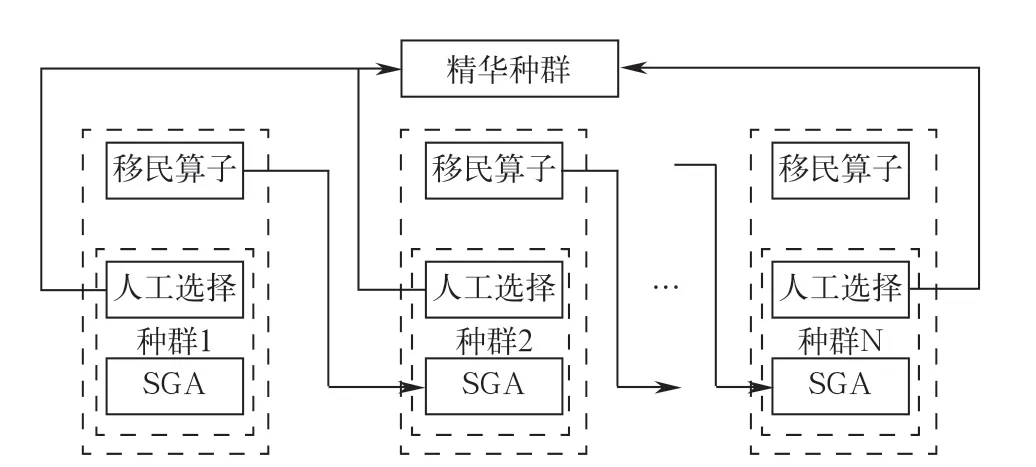
图3 MPGA操作示意图

4 仿真实例分析

4.1 Plant Simulation生产线建模

该硬质合金生产线在仿真平台中所建立模型如图4所示，模型中包括仓库以及配粉、球磨、干燥三道工序。三道工序中分别包含4台、16台、4台设备，工序间各设置有缓存区，工序间由AGV小车进行物料调度。

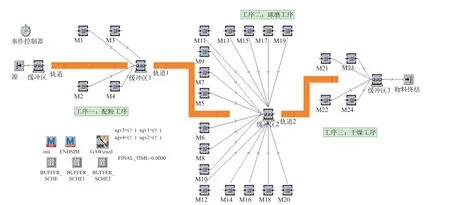
图4 基于Plant Simulation的生产线模型

按实际生产线布局在Plant Simulation平台中选取“Source”对象设置间隔时间模拟出库，模拟物料出入库；在各工序间添加“Buffer”对象用于模拟缓存区；分别选取4台、16台、4台“Singleproc”模拟配粉工序、球磨工序以及干燥工序的设备；分别建立“Track”、“Transporter”对象模拟AGV和AGV轨道。

4.2 调度方案优化

为优化本车间设备投产顺序，本文基于Matlab R2018b工具分别利用传统遗传算法和多种群遗传算法对设备投产顺序进行优化，运行环境为 Intel（R）Core（TM）i5-9300H 2.40 GHz，运行内存16GB。一批料共24个工件分别在设备数为4台、16台、4台的工序上依次加工，且不同工件在同一设备上的加工时间相同。为了方便多种群遗传算法与传统遗传算法对比，两种算法设置相同的最大迭代数和种群规模，设置最大迭代数为30，种群规模为40。其中多种群遗传算法随机产生5个初始子种群，为保证MPGA算法的全局搜索能力和进化种群的多样性，各种群采用不同的交叉概率和变异概率。在0.7～0.9范围内随机选择交叉概率，在0.01～0.05范围内随机选择变异概率。

两种算法优化后的投产方案与经验投产方案见表4。

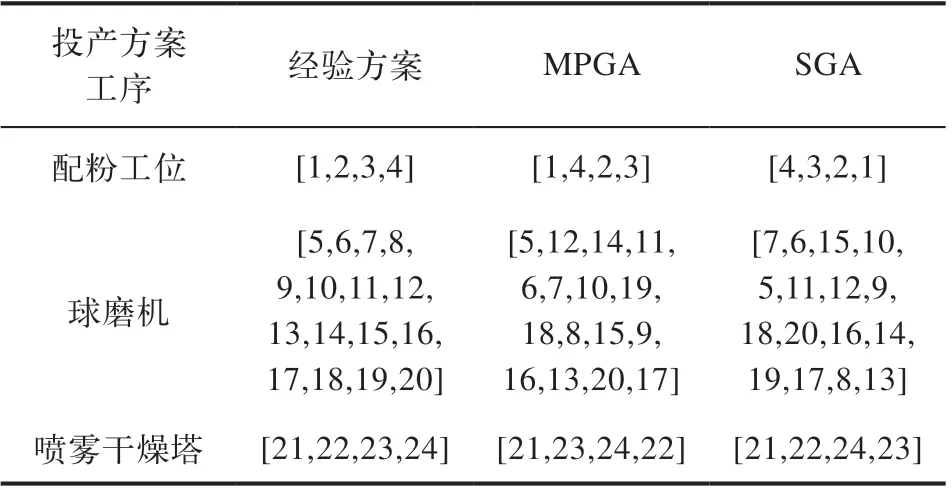
表4 经验方案与算法优化方案染色体对比

MPGA与SGA算法迭代过程图分别如图5、图6所示。

图5中横坐标代表迭代种群代数，纵坐标代表对应加工一批料所需时长。点画线代表每一代个体中最优的设备投产方案，虚线代表该代个体中最差的设备投产方案，“++”线为两者的平均值。

如图5所示，MPGA进化到第22代后，最优个体的目标变量FINAL_TIME才收敛于最小值，对比最大时间和最小时间曲线发现整个进化过程搜索邻域较大；如图6所示，SGA的进化曲线在第16代就已收敛于其“最小值”，且其搜索领域相对局限；上述结果证明MPGA有效地改善了SGA搜索邻域，且较好地克服了其“早熟”现象。

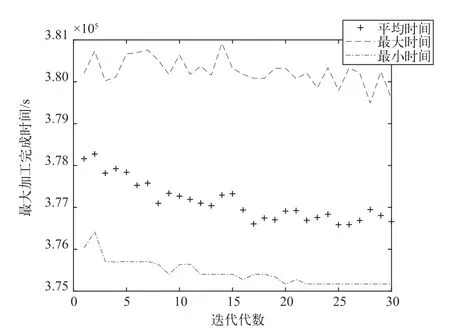
图5 MPGA排优迭代过程

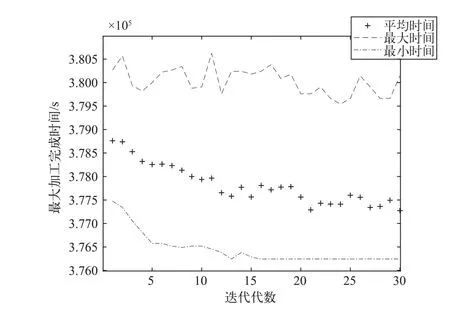
图6 SGA排优迭代过程

4.3 调度方案验证

在前文所建立的生产线模型中建立三个Table对象分别存放所得到的优化投产方案。建立一个全局变量FINAL_TIME，并在ENDSIM方法中将各投产方案得到的加工完成时间赋值给全局变量FINAL_TIME。建立Track、Track1、Track2对象，并各建立两个Onsensor方法对象。Onsensor1控制AGV从缓存区取料，Onsensor2控制AGV将物料按table表分配到各工序的设备上。

最终的仿真结果显示，MPGA相对传统投产方案优化了66 min；而SGA优化时间仅为18 min。

5 结束语

1）为提高硬质合金混合料生产效率，提出了一种改进的多种群遗传算法（MPGA）改善该硬质合金混合料生产线的生产调度方案。