基于ABAQUS仿真的尺寸偏差对密封性能的影响研究*

和建森 郭 飞 吴 凡 黄毅杰 祝世兴

(1.中国民航大学航空工程学院 天津 300300；2.清华大学摩擦学国家重点实验室 北京 100084)

密封结构在现代液压工业之中起着重要作用[1]。而O形密封圈又是密封结构中最为常见的构件之一，其看似结构简单，但在现代科学分析过程中想要对O形密封圈进行理论研究是非常困难的。近年来，为探究其密封性能国内外众多学者[2-15]通过有限元手段做出了诸多努力，通过建立O形橡胶密封圈轴对称模型，忽略密封结构尺寸偏差影响，借助非线性有限元手段，分析与研究O形圈主密封面在不同工作压力、不同压缩率下的接触压力变化规律，进而来评判O形密封圈的密封性能优劣。

在实际加工过程中，部件的尺寸偏差是不可避免的。存有不同尺寸偏差的构件装配在一起组成密封系统进行工作时，橡胶O形圈在使用过程中会产生不同的形变量(即压缩率不同)，使得密封端面处产生不同的接触压力分布，进而影响整体的密封效果。但尺寸偏差对密封结构可靠性的影响研究目前尚未发现。

本文作者为研究结构尺寸偏差对密封性能的影响，采用控制变量法研究了O形圈接触压力分布随尺寸偏差变化的规律；以最大接触压力为控制参量，通过不同尺寸组合的力学仿真分析，获取使最大接触压力呈现出最小状况的最劣尺寸组合，并以泄漏率为评判指标，探究不同配合间隙下(见图1)O形圈的密封性能，通过对比不同间隙下的泄漏率来分析运行过程中振动对挡板与沟槽配合的影响，从而为进一步提升O形圈的密封性能提供了参考。

图1 O形圈密封结构示意Fig.1 Schematic of O-ring sealing structure

1 方法分析

1.1 密封结构分析

图2及图3所示分别为O形圈和沟槽结构尺寸。图中包含的尺寸有橡胶O形圈的截面直径、内径，以及沟槽的截面宽度、槽深及槽边倒圆角5种参数。

文中从O形圈的尺寸偏差及沟槽的尺寸偏差两方面进行研究，其中O形圈的尺寸偏差考虑截面直径和内径偏差2种情况，沟槽的尺寸偏差考虑截面宽度、槽深及槽边倒圆角的偏差3种情况。采用控制变量法来研究上述不同因素的数值变化对密封界面最大接触压力的影响，同时提取相应接触压力分布，最终计算泄漏率。

图2 O形圈结构尺寸Fig.2 Size of O-ring structure

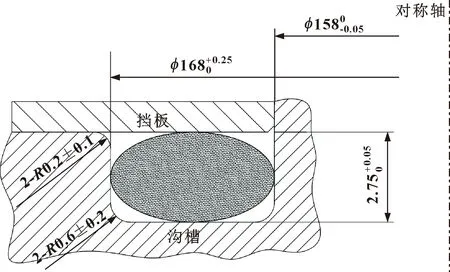
图3 沟槽结构尺寸Fig.3 Size of groove structure

首先，将公称尺寸作为初始分析数据，相关参数如表1所示。

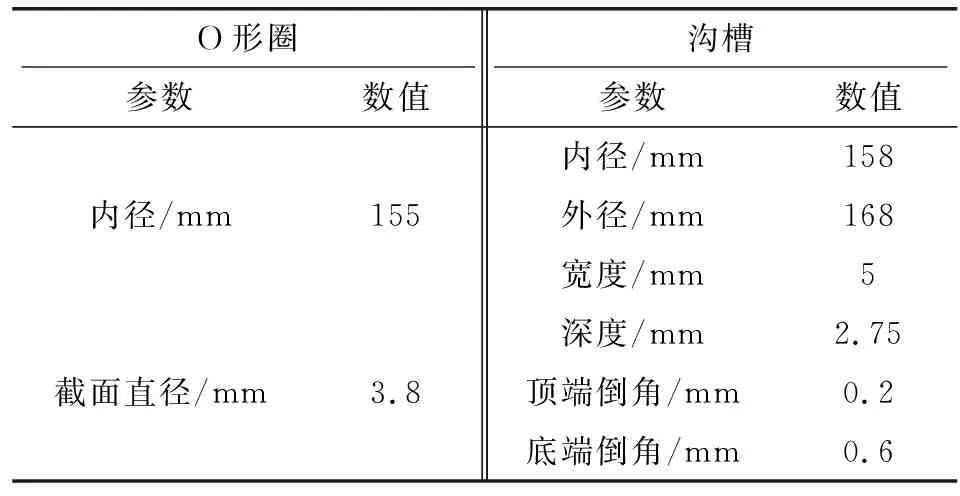
表1 初始装配结构尺寸Table 1 Initial assembly structure dimensions

将尺寸偏差变量作为对比分析，进行分情形讨论。分别从橡胶O形圈的结构尺寸和沟槽的结构尺寸两方面着手，基于图2及图3所示最大尺寸偏差将O形圈和沟槽结构尺寸依次进行变更，所得数据如表2所示。

表2 数据变量Table 2 The variable data of structure dimensions

1.2 有限元仿真

文中采用商用软件ABAQUS进行密封结构的静力学仿真。

为判断橡胶O形圈在存有结构尺寸误差的情况下是否可以可靠使用，对不同尺寸偏差组合的密封结构进行对比分析，选取其中2种情况来展现其变化关系，如表3所示，并基于图4展示其密封结构。

表3 不同尺寸组合的密封结构的压缩率Table 3 Compression ratio of sealing structures with different size combinations

从图4可以看出，随着结构尺寸的变化，橡胶O形圈在实际工作过程中其压缩率与接触宽度均有所不同。为提高计算效率，建模采用控制变量法，同时为使得计算仿真更容易收敛，假设密封件具有结构对称性，取O形圈密封系统进行二维轴对称几何建模。

对该模型施加图5所示的载荷和约束，依据实际使用过程，在第一个分析步中对沟槽施加指向为Ux=2 mm的位移约束，同时在第二个分析步中对挡板施加指向为Uy=2 mm的位移约束，其余约束均设置为固定约束。在第三个分析步中，对橡胶O形圈施加p1=0.4 MPa、p2=0.1 MPa的介质压力并采用压力渗透的方式进行模拟。对于温度场，在第一个分析步中将温度设置为25 ℃，在第三个分析步中将温度升至140 ℃，设置橡胶的热膨胀系数为2.056×10-4℃-1。

图4 不同尺寸组合的密封结构对比Fig.4 Comparison of sealing structureswith different size combinations

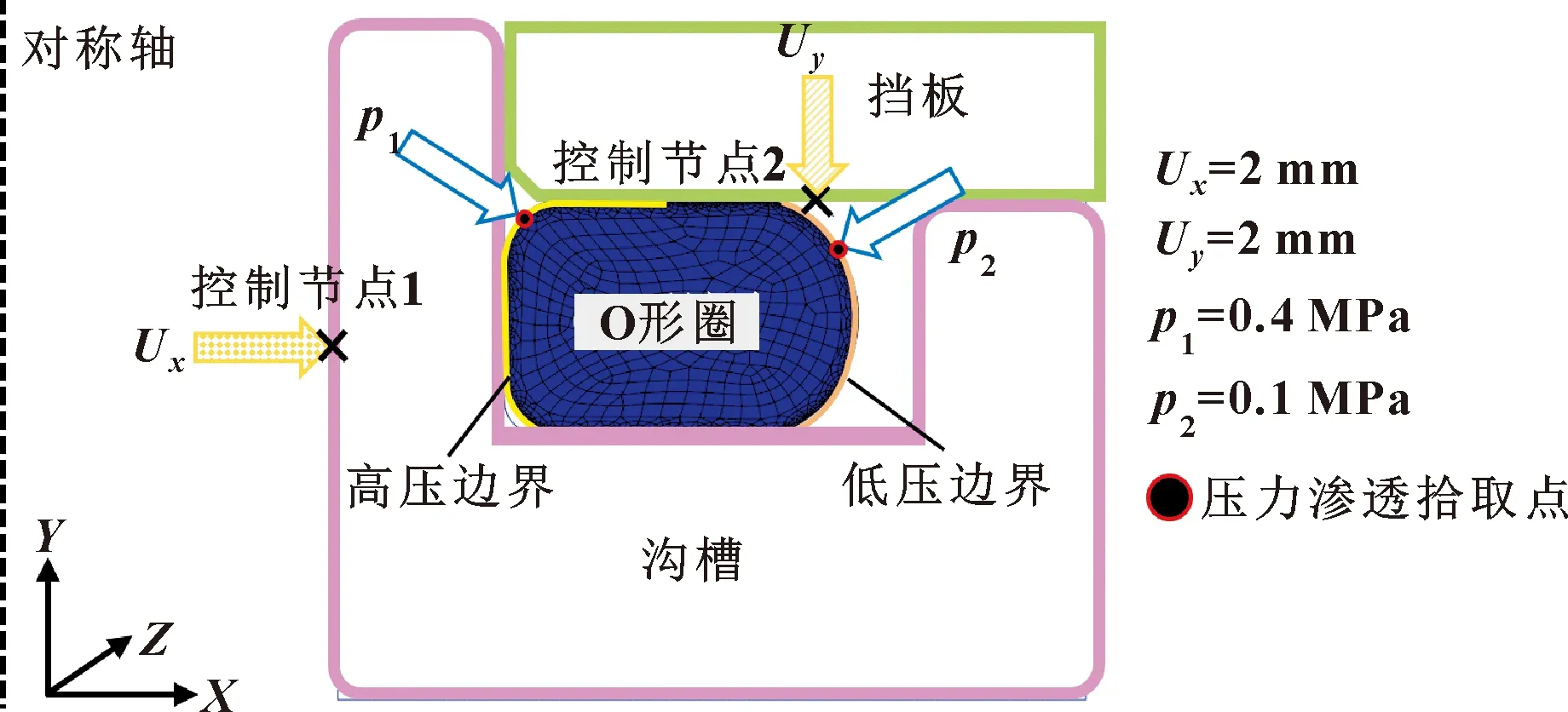
图5 密封系统几何模型及施加载荷与约束Fig.5 Geometric model of sealing systemand applied load and constraint

针对氟橡胶的超弹性不可压缩特性，设置其泊松比为0.49。在仿真计算过程中将氟橡胶单轴拉压测试应力应变数据导入材料属性参数中进行本构模型的拟合，拟合结果如图6所示。

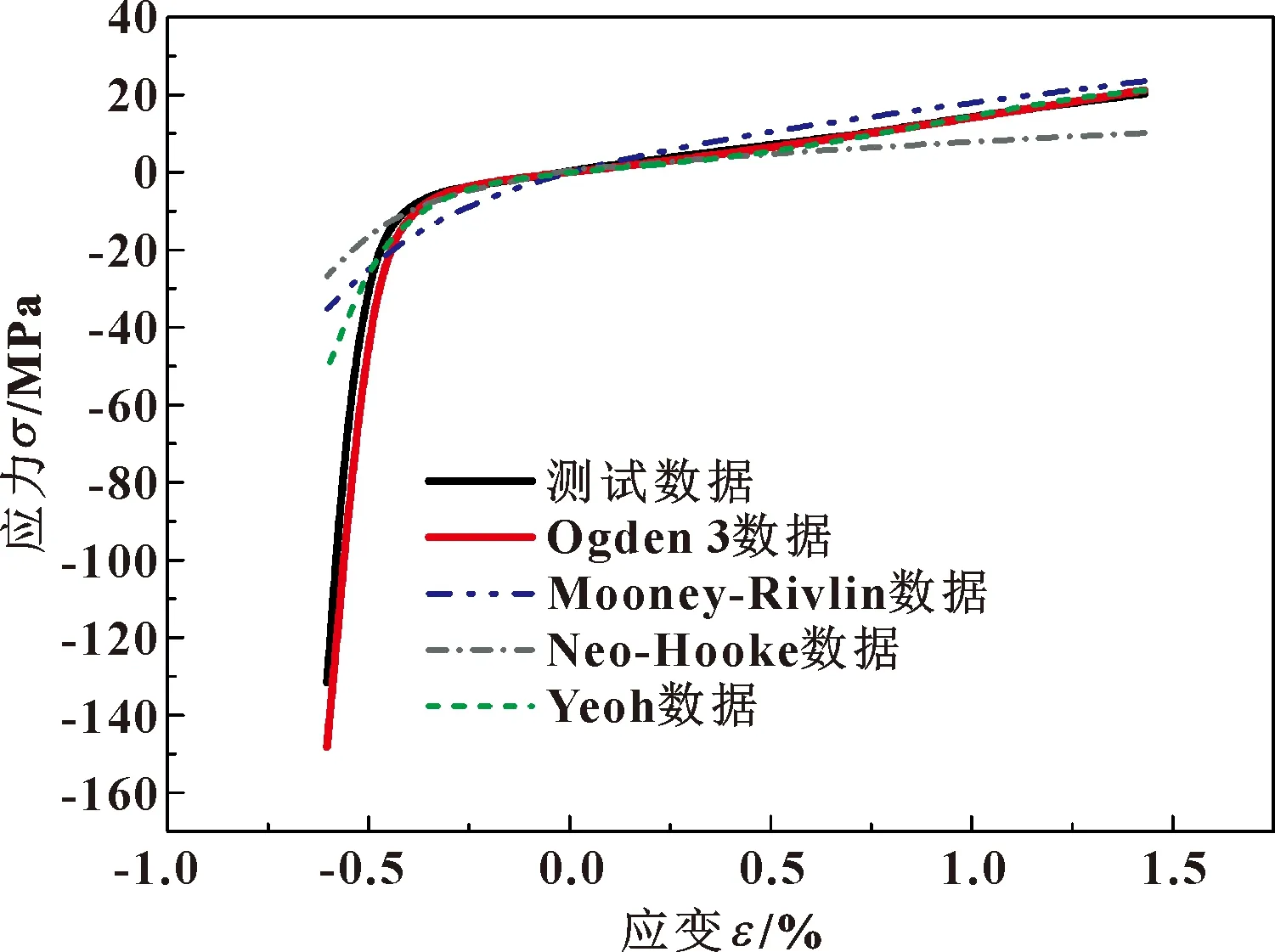
图6 材料参数拟合Fig.6 The fitting of material parameters

从图6可以看出Ogden 3阶模型曲线与测试数据具有较高的重合度，因此，最终选取Ogden 3阶应变能本构模型。Ogden 3阶的本构模型表达式为

(1)

式中：U为应变势能；N为Ogden模型阶数，N=3；J为橡胶材料的比体积；μi为材料参数， MPa；αi为无量纲参数；Di为不可压缩参数，用于表示体积变化；λi(i=1,2,3)为应变张量在3个方向上的主伸长率。

评估数据如表4所示。

表4 橡胶Ogden 3阶性能参数

1.3 密封特性分析

文中基于泄漏率及最大接触应力来判断系统密封性能的优劣。由于泄漏率是评估密封系统性能优劣的一项重要指标。因此，文中从计算泄漏率的角度出发，通过提取接触压力分布进一步计算泄漏率。在结构选取方面通过仿真来判断O形密封圈最大接触压力的变化情况，提取出最大接触压力值均小于其他情况组合下的接触应力分布，计算泄漏率。依此来判断系统在存有尺寸偏差的情况下，其密封性能的优劣。

2 结果与讨论

2.1 网格无关性验证

为使仿真结果更具有普适性，文中选取标准状态下的密封结构进行分析，探究橡胶O形圈在不同网格精度下的最大接触应力随间隙变化之间的关系，结果如图7所示。可以看出，当间隙相同、网格精度的选取在不超过0.08 mm的情况下，改变网格的精度，其最大接触应力值虽稍有波动，但对于计算结果基本无影响。而当网格精度超过0.08 mm时，此时的网格对最大接触应力值会稍有影响。根据网格无关性分析，文中采取不同网格精度下获取的最大接触应力求取均值的方式固定网格精度为0.02 mm，用于后续的有限元分析。

图7 网格精度与最大接触应力关系Fig.7 Relationship between mesh precisionand maximum contact stress

2.2 接触应力分析

2.2.1 O形圈结构尺寸对接触应力的影响

改变O形圈尺寸，分析了最大接触压力随其的变化关系，如图8所示。图8(a)所示为橡胶密封圈内径恒定为155 mm时，截面直径变化对橡胶密封圈接触区域接触压力的影响。可以看出，当内径不变时，截面直径由3.7 mm增大至3.9 mm其最大接触应力从3.004 MPa逐渐增大到3.736 MPa。图8(b)所示为橡胶密封圈截面直径恒定为3.8 mm时，内径变化对橡胶密封圈接触区域接触压力的影响。可以看出，当截面直径保持不变时，内径由153.8 mm增大至156.2 mm其接触压力最大值从3.38 MPa逐渐增大到3.686 MPa。因此，在保证其他因素不变的前提下，单一增大O形圈的截面直径或内径，其密封端面的最大接触压力呈现增大的趋势。

图8 O形圈尺寸变化与接触压力分布关系Fig.8 Relationship between O-ring size change and contactpressure distribution:(a)section diameterchange;(b)inner diameter change

2.2.2 沟槽结构尺寸对接触应力的影响

图9所示为其余结构尺寸保持不变的情况下，接触压力随沟槽深度的变化关系。

图9 沟槽深度变化与接触压力分布关系Fig.9 Relationship between groove depthand contact stress distribution

由图9可以看出，当沟槽深度为2.75 mm时，其对应的最大接触压力为3.658 MPa；而当沟槽深度增加至2.80 mm时，其对应的最大接触压力减小为3.375 MPa。这表明随着沟槽深度的增大，橡胶O形圈压缩量降低，其对应的最大接触压力减小。

图10所示为沟槽倒圆角的改变对接触压力的影响。由图10(b)可以看出，当底部倒圆角不变时，顶部倒圆角的变化对最大接触压力没有影响；当顶部倒圆角不变而底部倒圆角发生改变时，由于沟槽底部倒圆槽壁与密封圈之间发生接触(见图11)，接触压力增加，如图10(a)所示。

图10 沟槽倒圆角变化与接触压力分布关系Fig.10 Relationship between groove fillet change andcontact stress distribution：(a)bottom filletchange;(b)top fillet change

图11 底部倒圆角仿真示意Fig.11 The fillet simulation of bottom

图12所示为沟槽内外径变化对接触压力分布的影响。可以看出，随着沟槽内径的减小，橡胶密封圈的最大接触应力由3.658 MPa减小至3.645 MPa，发生微弱变化；而当外径发生变化时，接触压力分布曲线基本一致。产生这种现象的原因是在工作过程中，橡胶密封圈本身在低介质压力的作用下与沟槽外径内壁不发生接触，而沟槽内径的改变会使得密封圈的径向压缩率发生改变。文献[12]也表明压缩率越大，最大接触压力也越大。

图12 沟槽内外径变化与接触压力分布关系Fig.12 Relationship between inner and outer diameter changeof the groove and contact stress distribution:(a)inner diameter change of the groove;(b)outer diameter change of the groove

2.3 密封性能分析

在实际工况下由于振动的影响，沟槽与挡板之间便会形成间隙(如图13所示)，因此，文中分别取间隙值为0、0.15、0.3、0.45、0.6 mm进行泄漏率的计算。

基于2.2节分析结果，将呈现最大接触压力减小的情况进行组合，如表5所示。

图13 间隙仿真Fig.13 The simulation of clearance

表5 最大接触压力值最小时的密封尺寸组合Table 5 Size combination of sealing with minimum maximum contact pressure

将表5中数据导入有限元中进行仿真分析，将不同间隙下的接触压力分布进行提取，如图14、15所示。

图14和15所示为接触应力随两部件间隙的变化关系。通过对比图14与图15可知，当两者都处于最大压缩状态时，最劣尺寸组合的密封结构的最大接触压力远小于标准状态下。说明在该状态下最劣尺寸组合的密封结构发生泄漏现象的概率要远高于标准状态下。

图14 标准状态下接触压力分布与间隙关系Fig.14 Relationship between contact pressure distributionand clearance under standard condition

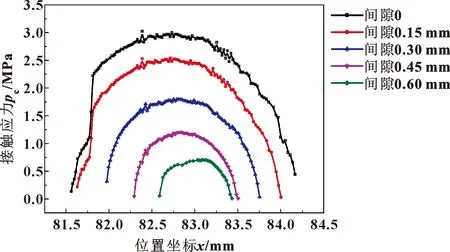
图15 最大接触压力为最小时接触压力分布与间隙关系Fig.15 Relationship between contact pressure distributionand clearance when the maximum contactpressure is the minimum

从图14和15还可看出，随着间隙的不断增大，最大接触压力不断降低，接触宽度也在不断减小，泄漏发生的概率逐渐增强。因此，文中通过取不同间隙下的接触压力来计算泄漏率，从而验证系统的可靠性。文中运用栅格渗漏模型及平行平板公式进行泄漏率求解。史建成[16]在PRESSON和YANG[17]建立的栅格渗漏模型基础上来实现泄漏通道的寻找，文中基于文献[16]的思路，通过将接触压力代入STANLEY模型[18]来计算出给定形貌变形后的接触矩阵及通道高度，将接触矩阵代入栅格渗漏模型来生成泄漏通道，最后基于平行平板公式计算出泄漏通道中的泄漏率。平行平板的泄漏率公式为

(2)

式中：Qv为体积流量；dx为泄漏通道的单位宽度(总长为O形圈周长)；h0表示截面泄漏通道形状为三角形的高度；hi(i=1、2)表示泄漏通道的截面形状为梯形的高度；μ为流体的动力学黏度，此处取值5.434 6×10-3Pa·s；dy为泄漏通道的单位长度(总长为接触宽度)；Δp为密封面两端的压差，取值0.3 MPa。

图16所示为间隙与泄漏率的关系。随着挡板与沟槽之间间隙的不断增大，泄漏率都呈现逐渐增大的趋势。而随着间隙进一步增大，最大接触应力最小时的组合(记为最劣情况组合)的泄漏率明显要高于标准尺寸组合。产生这种现象的原因是在该组合下橡胶密封圈直径相对减小和沟槽深度相对增加，使得密封接触区域及密封接触压力都较标准组合减小，从而引起泄漏量的增大。

图16 不同尺寸组合的密封的间隙与泄漏率关系Fig.16 Relationship between clearance and leakagerate of seals with different size combinations

3 结论

利用ABAQUS软件对存有尺寸偏差的密封结构进行有限元仿真分析,探究结构尺寸偏差对结构组合密封性能的影响。具体结论如下：

(1)通过控制变量法获得不同尺寸偏差下橡胶O形圈的接触压力分布、最大接触应力的变化规律。结果表明：当沟槽不存在尺寸偏差时，增大O形圈的截面直径或内径，其密封端面的最大接触应力呈增大趋势；而当O形圈不存在尺寸偏差时，沟槽内径的增加、底部倒圆角的增大以及沟槽深度的增大都会使得密封端面的最大接触压力呈现出增大的趋势。

(2)通过对比不同尺寸偏差下的接触压力分布及最大接触压力的变化规律，推导出当密封结构的尺寸选取最大接触压力最小的组合时，随着密封结构间隙的不断增大，密封面泄漏率不断增加，其密封性能相较于标准参数组合密封较差。

(3)在沟槽结构存有尺寸偏差的情况下，通过O形圈的合理选装可以进一步提升密封性能。如当沟槽内径偏小时，可选装内径为标准值而截面直径较大的O形圈来增大其接触宽度及接触应力，进而保障部件的正常运行。