阶跃载荷下气体轴承-转子系统瞬态特性流固耦合分析*

丁 一 马文琦 孙培耕 邱习强

(大连海事大学船舶与海洋工程学院 辽宁大连 116026)

机床加工过程中，主轴精度是影响产品质量的关键因素，气体轴承-转子系统是主轴系统中的关键部件。在瞬态变载荷工况下，气体轴承-转子系统中的转子运动与气膜流场间存在强耦合作用，对气体轴承-转子系统进行流固耦合瞬态特性分析，有助于研究系统受瞬变载荷瞬间的系统响应，对指导实际加工，提高加工精度有重要意义。吴斌[1]基于流固耦合法，针对静压止推轴承在承载过程中气膜间隙的变化，给出了主轴高速旋转时的承载力特性曲线。WANG等[2]采用有限体积法给出了流固耦合作用下气膜间隙在不同负载下的非线性振荡特性。YU等[3]采用流固耦合的手段预测了滑动轴承在重载下因系统结构形变而造成的油膜间隙沿半径方向的变形规律。WODTKE等[4]使用流固耦合的方法，研究了水润滑轴承的动静压效应和固体变形对流场压力的影响。赵自强[5]建立了轴承-转子系统流体-固体耦合模型，并在CFD分析软件中运用流固耦合法对该模型进行流固耦合分析计算，进而获得主轴的变形量以及变形引起的静压气体轴承静态特性的变化。针对静压径向轴承在承载过程中出现的轴颈倾斜现象，杨彦涛和王海博[6]采用理论分析结合MATLAB仿真的方法研究了不同倾斜角下转子系统承载特性的变化，得到了一定偏心率下倾斜角度和承载力等特性的变化规律。JENG和HUANG[7]研究了不同材料对轴承动态特性的影响规律并总结了不同转速、润滑条件、工作载荷下轴承动态特性的变化规律。JORGENSEN和SHIN[8]对轴承-转子系统进行动力学建模并研究了不同切削载荷、进给速度及旋转速度下系统动态特性的变化规律。对于阶跃载荷对转子系统的影响，何芝仙等[9]选择使用ADAMS和MATLAB联合仿真的手段，研究了油润滑轴承受到阶跃载荷冲击时的动力学响应和轴承的摩擦学特性。LAI等[10]分析了轴承结构刚度和阻尼特性对转子-箔片-轴承系统稳定运行的影响，通过静载荷和挠度试验，得到了径向滑动轴承和推力轴承的静态结构刚度和阻尼系数。李昊等人[11]从超调量、超量时间和轴心偏心量等角度分析了可倾瓦轴承在阶跃载荷下的动态响应。关岱杉和郭百森[12]通过有限差分法求解动载滑动轴承的雷诺方程，对比分析了阶跃、正弦、孤峰波形冲击作用下滑动轴承油膜压力分布特征。田尚沛[13]以高速电主轴为研究对象分析了转速、预紧力、轴承参数以及热变形之间的关系。ZHANG等[14]研究了预紧力对转子-轴承系统振动的影响，结果表明预紧力对系统振动大小有不可忽视的影响。李纯洁等[15]将实验与仿真相结合，得出不同转速下轴承预紧力对轴承动刚度的影响规律，进而指出可以通过调节预紧力以增强轴承刚度。

目前大多数学者在研究气体轴承-转子系统时往往忽略气体轴承支承气膜流场与转子运动姿态之间的流固耦合作用及实际工况下负载瞬态激励对转子轴心偏移的影响。因此，本文作者以气体轴承-转子系统为研究对象，通过双向流固耦合数值仿真，分析不同阶跃载荷激励下轴承气膜流场不同时刻下的压力分布特性，以及气体轴承-转子系统的转子超调量、超调时间、稳定时间等特性的影响因素和变化规律。

1 流固耦合仿真模型建立

1.1 系统模型

气体轴承-转子系统结构如图1所示，采用环面节流形式的径向气体轴承，止推气体轴承和径向止推联合气体轴承构成了系统中的轴承组。轴承-转子系统在高转速运转及承受负载条件下，气膜流场特性与转子偏移、受力分布相互影响，因此需对其进行双向流固耦合分析。铣削过程中，转子受到铣刀铣削工件带来的力简化为y方向的载荷F。当转子受载后，处于倾斜状态，转子中心线如图1中虚线所示。两端径向轴承承载力分别为W1和W2，结构参数如表1所示。

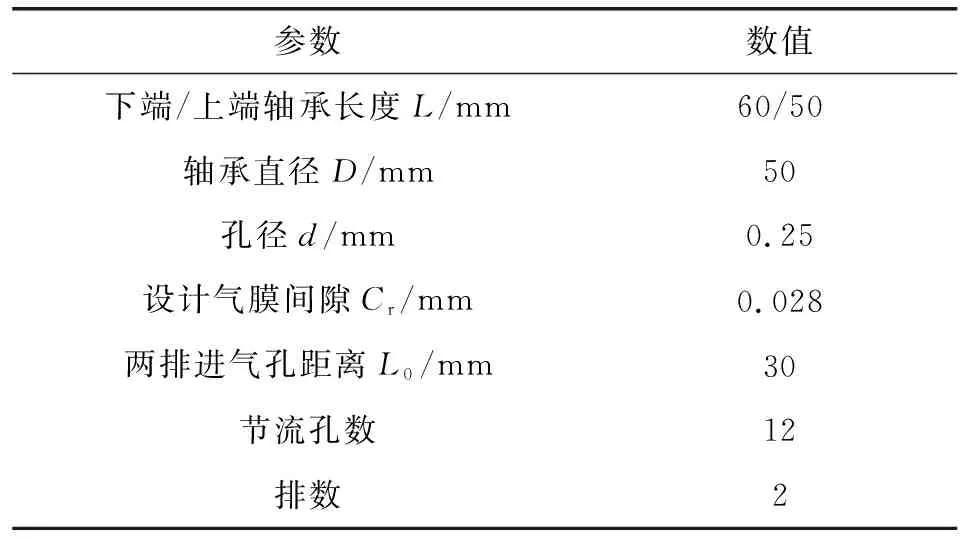
表1 径向轴承结构参数Table 1 Structural parameters of radial bearing

1.2 网格划分及求解设置

图2(a)和图2(b)所示分别为转子和气膜流场模型。流场的三维模型由多个部分组成，分别为径向止推气体轴承、止推气体轴承和径向气体轴承气膜模型。转子建模过程中，单独建立与流场对应的耦合面，以方便进行流场与固体场之间的数据传输。转子固体场网格全部采用结构性网格；采用分区画法将流场网格分为气膜与节流孔两部分，其中气膜网格分成12个区域，采用结构性网格，节流孔区域附近采用非结构性网格，并进行网格加密。

以径向轴承节流孔附近压力分布及承载力为无关性验证对象，对比分析网格数分别为77万、120万与200万的仿真计算结果。结果发现，77万网格数量时的承载力与其他2种网格数量时相差较大，120万网格数与200万网格数的节流孔附近压力分布及承载力的计算结果偏差较小。考虑计算效率和网格数对数值仿真结果的影响，文中采用120万网格数进行数值仿真。

流固耦合模型边界条件及相关参数设置如下：

(1)外部环境压力p0=0.101 MPa，环境温度T0=300 K，流体介质选择理想气体；

(2)转子和流场的接触面设置为流固耦合数据传输面，节流孔入口供气压力ps=0.6 MPa(相对压力)，流场出口压力为环境压力p0；

(3)选择离散、隐式求解器，湍流模型为SSTk-ω模型。

2 阶跃载荷下轴承-转子系统瞬态响应分析

2.1 转子动态响应分析

铣刀与工件接触瞬间所产生的阶跃载荷将导致转子刀头位置突变，使气膜瞬间产生压缩，严重时会出现抱轴现象。为了研究铣削过程中转子的动态特性，对简化后的转子下端刀头位置施加图3所示的稳态和矩形2种类型阶跃载荷。

以上升时间tr、超调时间tp、最大超调量Mp和稳定时间ts等系统瞬态响应参数作为性能指标的系统,在阶跃载荷作用下位移响应特性曲线如图4所示。

图5所示为上、下端径向轴承在200 N阶跃载荷作用下，承载力随时间的变化。结果显示，上、下轴承支承承载力都出现振荡过程，超调分别达到了497.5和142.3 N，振荡后达到平衡。此时，上下端径向轴承的承载力方向相反且下端轴承承载力大于上端径向轴承。文中以下端径向气体轴承为主要研究对象，分析系统在阶跃载荷下的瞬态响应特性。

图6所示为不同阶跃载荷下转子位移响应，3个时刻分别代表系统超调过程中的最大偏移时刻TA、最小偏移时刻TB和稳定时刻TC。对比结果可看出，在不同阶跃载荷作用下，转子位移响应变化规律一致，200 N阶跃载荷作用下，转子偏移幅值明显大于100 N阶跃载荷，且阶跃载荷越大，转子超调量、最大振幅越大，调节稳定后转子偏斜位移值增大，但系统的超调时间tp和最终的稳定时间ts都有所缩短，稳态阶跃载荷下系统的动态特性参数如表2所示。

分析图6中矩形阶跃载荷作用下转子刀头处的位移变化和表3中矩形阶跃载荷的超调时间tp可知：在0～10 ms阶段，100 N稳态阶跃载荷与矩形阶跃载荷下转子动态响应变化规律基本一致，经过6.5 ms后达平衡位置。在t=10 ms时刻，外负载在从100 N阶跃到200 N，转子经过4.1 ms后到达平衡位置，与200 N下稳态阶跃载荷相比，二次阶跃载荷下转子响应更快，滞后性较低。

相比200 N稳态阶跃载荷下的动态特性，10～20 ms阶段，矩形阶跃载荷下系统性能提高比例如表4所示。

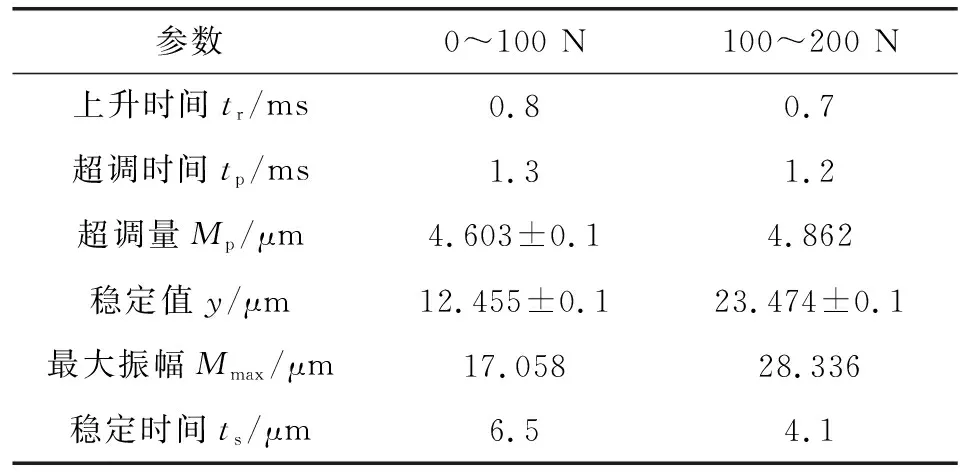
表3 矩形阶跃载荷下系统动态特性参数Table 3 System dynamic characteristic parameters under rectangular step load

表4 矩形阶跃载荷下系统性能提高比例Table 4 System performance improvement ratio under the rectangular step load

由表4结果可知，矩形阶跃载荷下系统稳定性能明显提高。原因是矩形阶跃载荷下，10 ms时系统已在外载荷的作用下达到耦合平衡，气膜已经具有一定的刚性，系统也有一定抗载荷能力，在此基础上外载荷突然增大，气膜刚性抑制了转子大幅度偏移，转子超调量减小。故预载荷有助于提高系统瞬态响应下的稳定性。

2.2 轴承流场特性分析

图7所示为转子中心线在100～200 N矩形阶跃载荷下的位移及形变。3个时刻同样分别代表系统超调过程中的最大偏移时刻TA、最小偏移时刻TB和稳定时刻TC。结果显示，在流固耦合过程中，受到载荷和气体轴承承载力的共同作用转子发生倾斜偏移和轻微弯曲变形现象。

图8所示为不同时刻气膜流场压力云图。从图8(a)可以看出，轴承流场周向压力变化明显，沿转子轴向偏斜导致气膜厚度轴向的非均匀性，压力分布沿轴向也出现非均匀现象，轴承下端倾斜带来的更高的气膜压缩量导致流场压力更高。图8(b)和图8(c)中气膜压力因转子倾斜造成的压力分布沿轴向非均匀性相对较弱。

图9给出了矩形阶跃载荷下承载力随时间的变化。从图7—9可以看出，伴随着转子因阶跃载荷的超调偏移，气膜间隙大小的波动直接影响了流场内的压力分布，进而影响气膜承载力随时间的变化。

矩形阶跃载荷下系统y向受力情况如表5所示。图9中TA时刻下端径向轴承承载力超调量最大，轴承y向承载力大于负载，因此转子y向偏移量减小，向反方向偏移；至转子偏移量最小的TB时刻，轴承y向承载力小于负载，转子y向偏移量增大，在径向轴承承载力与载荷的共同作用下，转子往复振动直至趋于动态平衡状态；在TC时刻，轴承y向承载力与负载相近，系统趋于平衡。

表5 矩形阶跃载荷下系统y向受力变化Table 5 Variation of the y-direction force of the system under rectangular step load

图10给出了200 N稳态阶跃载荷和矩形阶跃载荷在负载瞬变时的流场压力变化。可知，在同样承受200 N载荷的情况下，矩形载荷的超调时刻的压力变化较小，仅在压力等级为7以上的承载区域有略微的变化，压力变化较为平稳; 而在200 N稳态阶跃载荷下，压力等级8以上的高压区域出现明显的压力波动，反映到实际工况下将造成转子轴心轨迹紊乱、加工精度降低等负面影响。从图10(a)和图10(c)可以看出，2种不同载荷形式下超调位置处流场的高压区域出现明显差别，图10(c)所示的200 N稳态阶跃载荷下压力较大且高压区域较广，主要是由于此时气膜压缩量较大造成的。由上述分析可知，过高的压缩量将会导致气膜更剧烈的回弹进而影响转子回转精度，预载荷对于减小流场压力波动从而增加转子系统稳定性具有重要意义。

3 加载实验

气体轴承-转子系统测试试验台如图11所示。试验台主要包括气体轴承-转子系统、加载装置、压力控制采集系统以及位移信号采集系统。试验台中转子位移、加载力信号和压力信号采集与控制通过采集卡连接到计算机的LabView程序中。

图12和图13所示分别为200 N阶跃加载和100～200 N矩形阶跃加载试验测试与数值仿真模拟结果对比曲线，其中T0为测试总时长。可知：试验测试与仿真结果变化趋势一致，但由于系统响应及测试误差等原因，试验偏移量曲线略滞后于仿真曲线。在200 N单一阶跃加载条件下，试验测试转子最大偏移量为32.5 μm，稳定后偏移量约为27 μm，略大于仿真值。在100～200 N矩形阶跃加载条件下，转子最大偏移量为28.8 μm，相比200 N阶跃加载试验下最大偏移量减小3.7 μm，与仿真结论一致，即矩形阶跃加载时气膜已经具有一定的刚性，系统抗干扰能力更强，稳定性更好。

4 结论

(1)系统受载时，气膜流场压力分布沿轴向出现非均匀分布现象，转子下端轴承处气膜偏心更大，压力更高，承载力更大。

(2)系统所受到的稳态阶跃载荷增大时，虽然系统的超调时间和最终的稳定时间都有所缩短，但转子超调量随之增大，气膜压缩量增大，影响转子回转精度从而影响加工质量。

(3)矩形阶跃载荷使得气膜具有一定的刚性，进而使得流场压力波动减小，转子超调量明显减小，且转子的稳定时间也有所缩短，即预载荷能使系统在载荷瞬变情况下的刚性和抵抗能力明显增强，有助于提高实际加工过程中的加工质量。