内配格构式钢骨钢管混凝土构件的抗弯性能

王先铁，庞亚红，高欢，韩军科，朱彬荣，谢川东

(1.西安建筑科技大学 土木工程学院，西安 710055；2.中国电力科学研究院有限公司，北京 100085)

格构式钢骨钢管混凝土构件是指在钢管混凝土柱中埋入钢骨(角钢)，钢骨之间用缀板连接，并在钢管内壁焊接纵向加劲肋的一种新型组合构件。与传统钢管混凝土构件相比，钢骨和纵向加劲肋可增强钢材对核心混凝土的约束，从而提高构件的强度和刚度，减小外钢管的厚度；混凝土可防止钢骨与加劲肋的局部屈曲。与内配工字钢、交叉工字钢等钢管混凝土构件相比，格构式钢骨离截面中和轴较远，可增大受弯构件的截面模量，改善截面的力学性能，在同等约束条件下可减少钢材用量。目前，学者们对内配纵向加劲肋、工字钢、钢骨等钢管混凝土构件的力学性能开展了一系列研究。Kitada[1]对钢管壁焊接纵向加劲肋的钢管混凝土构件进行了试验研究，结果表明，在钢管壁焊接纵向加劲肋能改善钢管的稳定性，延缓钢管的局部屈曲，增强钢材对核心混凝土的约束作用，从而提高构件的承载能力。Zhu等[2]对26个钢骨方钢管高强混凝土柱进行了轴心受压试验，结果表明，钢管混凝土构件内配钢骨能改变构件的破坏模式和屈服后的性能。Chen等[3]对内配角钢的钢管混凝土柱进行了轴拉试验，结果表明，配有钢筋或角钢的钢管混凝土柱弹性刚度提升较为明显，承载力提升有限。Elchalakani等[4]、Kennedy[5]对矩形、方形、圆形钢管混凝土构件进行了纯弯试验，结果表明，钢管与混凝土能协同工作，并且钢管内填充混凝土可提高构件的强度和延性。Chang等[6]采用有限元方法对钢骨钢管混凝土柱的力学性能和破坏机理进行了对比分析，结果表明，钢骨钢管混凝土柱比普通钢管混凝土柱具有更高的承载力和刚度。何益斌等[7]对2个钢管混凝土构件、11个钢骨钢管混凝土构件进行了偏心受压试验，结果表明，内置钢骨可有效提高钢骨钢管混凝土构件的偏压极限承载力。王博等[8]采用统一强度理论对轴心受压钢骨组合L形钢管混凝土短柱的核心混凝土、型钢钢骨在三向受压应力状态下的极限承载力进行了分析。刘晓等[9]对配有工字形钢骨的钢管高强混凝土构件进行了抗弯试验，主要研究参数为配骨指标和钢骨加载方向(强轴和弱轴)，结果表明，极限弯矩随配骨指标的增加呈非线性增长。徐菲等[10]对4组格构式钢骨钢管混凝土柱进行了轴压试验，结果表明，钢骨钢管混凝土柱的受力过程均经历弹性阶段、屈服阶段和破坏阶段，钢骨能与钢管、混凝土共同工作，协同变形。查晓雄等[11]对内配钢筋、圆钢管及工字钢的钢管混凝土构件进行了纯弯试验，并给出承载力计算公式，结果表明，内配加劲件的钢管混凝土构件在纯弯作用下具有较好的延性。

综上所述，学者们对内配纵向加劲肋、工字钢、钢骨等钢管混凝土构件的受压、受弯性能开展了一些研究，但对具有良好力学性能的格构式钢骨钢管混凝土组合构件缺乏充分的试验和理论研究。笔者对外钢管带纵向加劲肋、同时内配格构式钢骨的钢管混凝土构件的受弯性能开展研究，探究该类构件在纯弯荷载作用下的受力性能、破坏模式，明确其受力机理，并采用相关规范对试验试件的抗弯承载力和刚度进行计算，将计算结果与试验结果进行对比。

1 试验概况

1.1 试件设计与制作

试验设计了4组共8个试件，每组2个试件完全相同，试件长度为3 000 mm，试验主要变化参数为试件钢管是否配有纵向加劲肋或试件是否内配格构式钢骨。试件编号分别为CW-1-1～CW-4-2。其中，CW-1为普通钢管混凝土试件，CW-2为钢管设置纵向加劲肋的试件，CW-3为内配格构式钢骨的试件，CW-4为钢管设置纵向加劲肋、同时内配格构式钢骨的试件。为了对比内配格构式钢骨钢管混凝土试件在不同方向的抗弯性能，加载时，每组的1号试件使内配格构式钢骨的实轴通过加载平面，2号试件使内配格构式钢骨的虚轴通过加载平面，即每组的2号试件均相对1号试件旋转45°放置。试件主要参数如表1所示，试件整体构造图和截面形式如图1、图2所示。

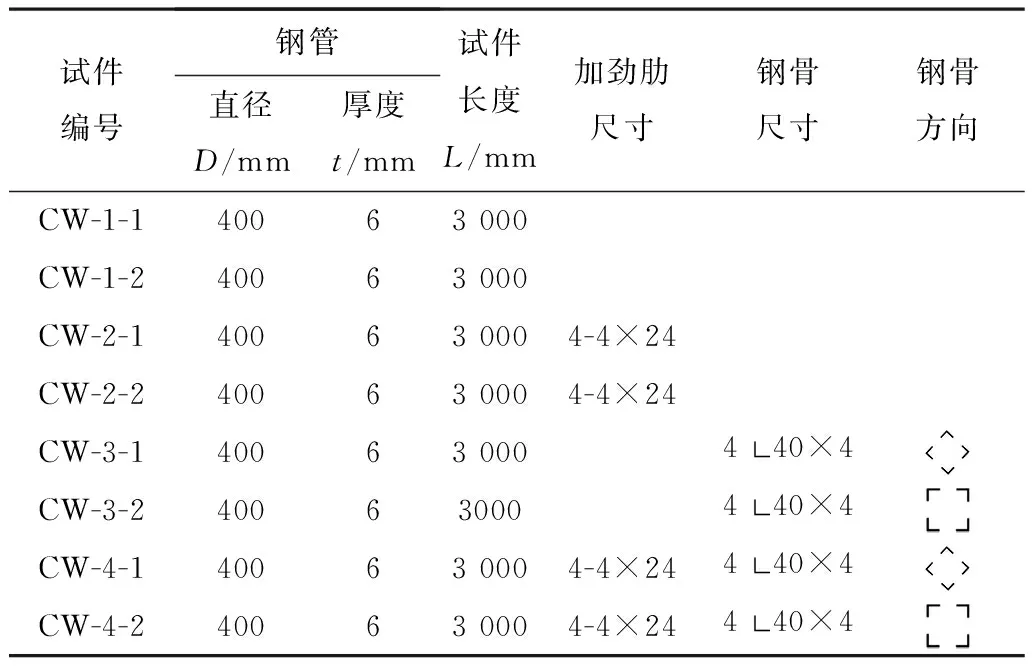
表1 试件参数

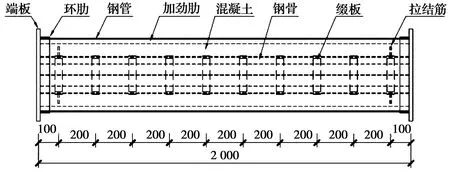
图1 试件整体示意图

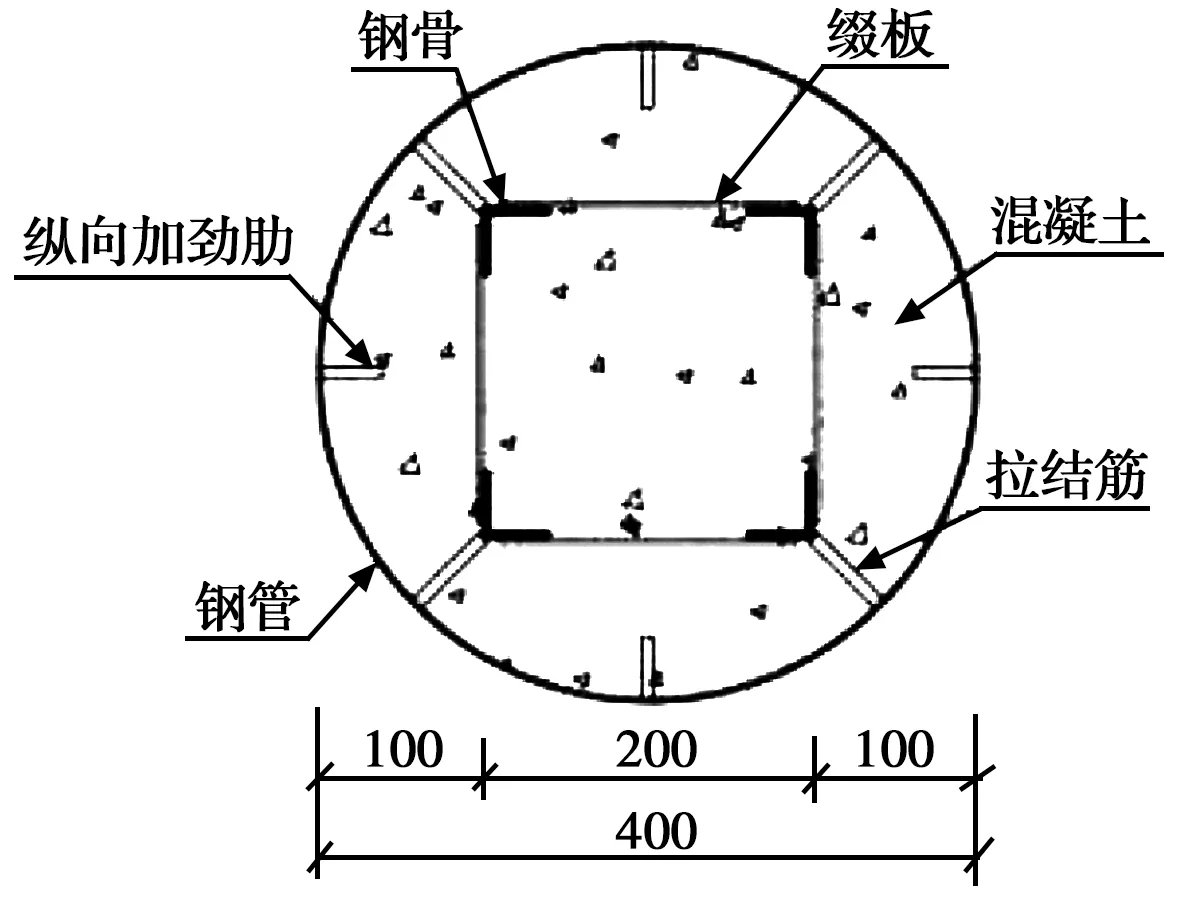
图2 截面示意图

1.2 材料力学性能

钢管和角钢强度等级分别为Q345B和Q235B，按照《钢及钢产品力学性能试验取样位置及试验制备》(GB/T 2975—2018)[12]的要求分别在不同强度的钢板上沿纵向切割标准试样，每组3个，按《金属材料室温拉伸试验方法》(GB/T 228.1—2010)[13]进行钢材拉伸试验，钢材材性试验结果如表2所示。

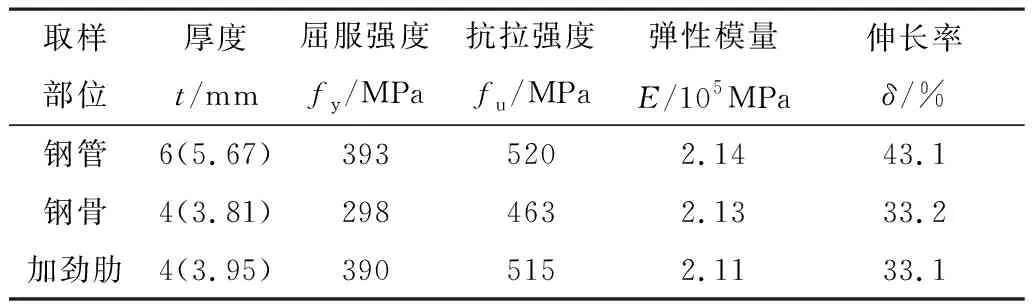
表2 钢材材性试验结果

混凝土强度等级为C50。按照《混凝土物理力学性能试验方法标准》(GB/T 50081—2019)[14]的相关要求进行试样制作和养护，28 d后测得混凝土轴心抗压强度fcu为53.5 MPa，弹性模量Ec为3.53×104MPa。

1.3 加载装置与测量方案

试验在500 t电液伺服压力试验机上进行，试验装置如图3所示，采用三分点加载方式。为模拟简支边界条件，制作了两个带有一定宽度的弧形支座，如图3所示，左侧支座只允许试件发生绕垂直于加载面方向的转动，右侧支座只允许试件发生轴向位移和绕垂直于加载面方向的转动。

图3 试验装置

测点布置如图4所示。在试件跨中截面间隔布置纵向和环向应变片，在纯弯段四分点处间隔布置环向应变片，以测量试件纯弯段各截面的纵向和环向应变。在试件支座、加载点、跨中位置布置位移计，以测量试件的竖向位移。

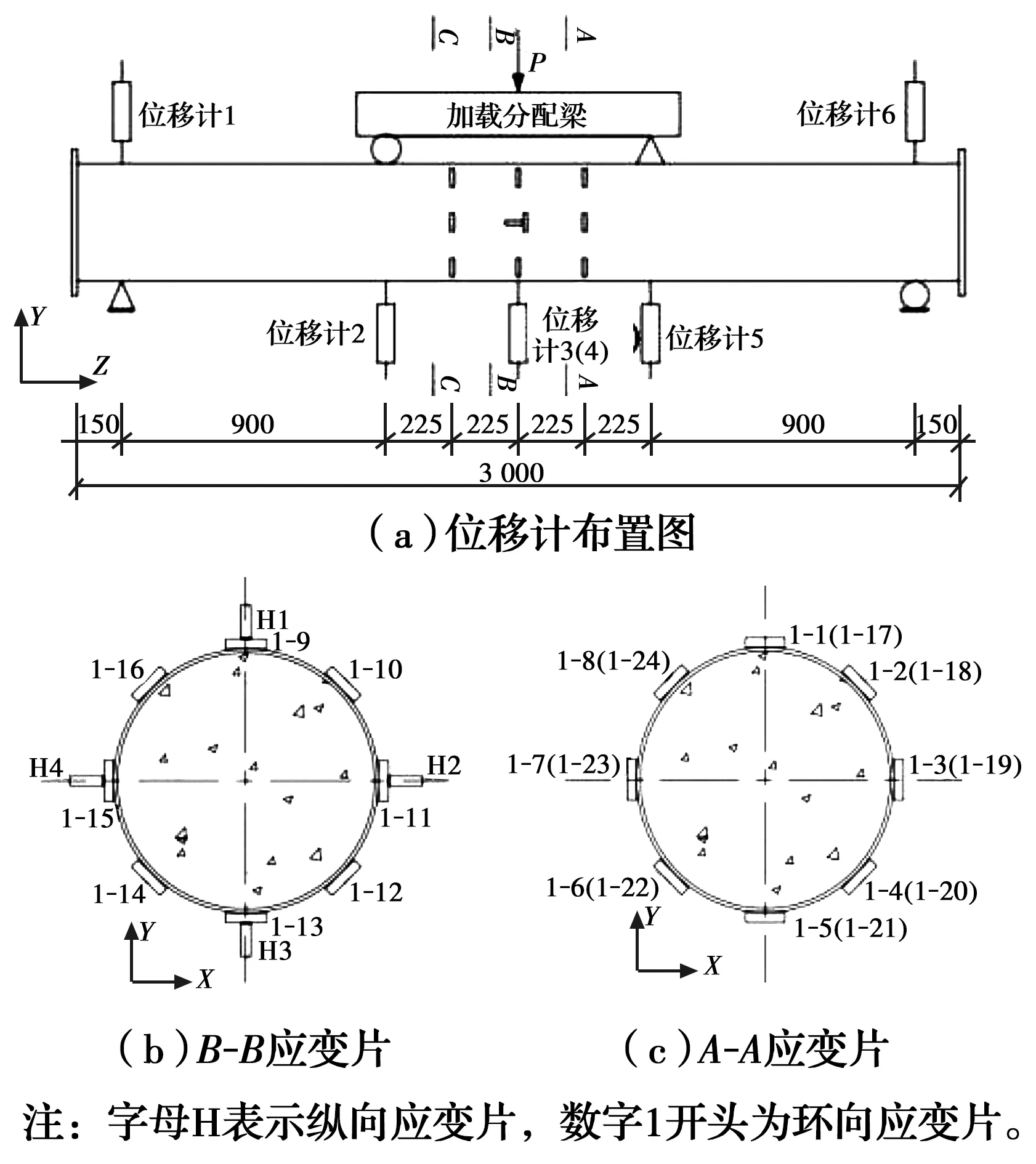
图4 测点布置Fig.4 Arrangement of measurement

为了检查试验装置、测试仪器是否正常工作，先预加载2次，第1次加载至承载力设计值的60%，再卸载到0%，如此再反复一次。第3次加载采用分级加载，弹性范围内荷载级差为5 kN，持荷2 min后，再施加下一级荷载；当荷载达到约60%预估极限荷载后，慢速连续加载；跨中最大挠度δm超过L/50(L为试件长度)后，采用δm控制加载至破坏。

2 试验结果

2.1 试验现象及破坏模式

各组试件试验现象和破坏形态基本一致，如图5所示。加载初期试件均无明显变化，随着荷载的增加，试件轻微弯曲，荷载进一步增加，试件跨中挠度不断增大，两端向上翘起，弯曲逐渐明显；同时，由于在加载点卡槽处应力集中，内部混凝土局部压碎，钢管在加载点处轻微鼓曲。整个加载过程中，试件均表现出优异的延性和变形能力；由于混凝土对钢管壁的支撑作用，各试件纯弯段钢管均未出现局部鼓曲，图6为试件CW-4-2在加载过程中挠度沿试件长度的变化情况。由图6可知，试验过程中，内配格构式钢骨钢管混凝土试件的挠曲线基本呈对称的正弦半波曲线。

图5 试件破坏形态

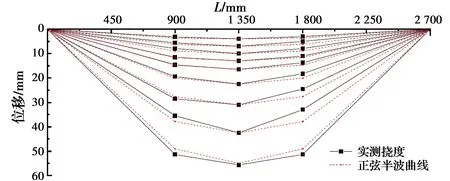
图6 试件CW-4-2挠度曲线Fig.6 Deflection curves of CW-4-2

试验结束后，割开部分试件的外钢管，观察试件受拉区、受压区内部混凝土的破坏情况，如图7所示。由图7(a)可以看出，试件CW-3-1受压区混凝土出现纵向裂缝，表明试件破坏时受压区混凝土在压应力作用下被劈裂，裂缝沿长度方向发展，但宽度方向较小。对比不同组试件受拉区混凝土裂缝的开展情况可知：与配有格构式钢骨的试件CW-3相比，仅设有纵向加劲肋的试件CW-2受拉区裂缝间距更小，分布更为密集；试件CW-3与同时设有纵向加劲肋和格构式钢骨的试件CW-4裂缝开展情况相似。由此可知，试件内设格构式钢骨能有效减少受拉区混凝土裂缝的产生，其原因为格构式钢骨增强了试件的整体性，对混凝土的约束作用更强，在受力过程中可为受拉区混凝土分担更多的拉力，从而延缓受拉区混凝土裂缝的产生和发展。

图7 混凝土开裂情况

2.2 弯矩-跨中挠度曲线

各组试件的弯矩-跨中挠度曲线如图8所示。加载时，CW-1组试件放置方式相同，因此两个试件的弯矩-跨中挠度曲线基本重合；CW-2、CW-3、CW-4组试件第2个试件均相对第1个试件旋转45°放置，当中和轴位于形心轴时，上述两种不同放置方式的试件截面惯性矩相同。加载过程中受弯试件受拉区混凝土抗拉能力较差，实际中和轴位置高于形心轴，导致二者在受力过程中截面惯性矩和抗弯刚度有所不同，故每组两个试件的刚度和极限承载力并不完全一致，但相差不大。

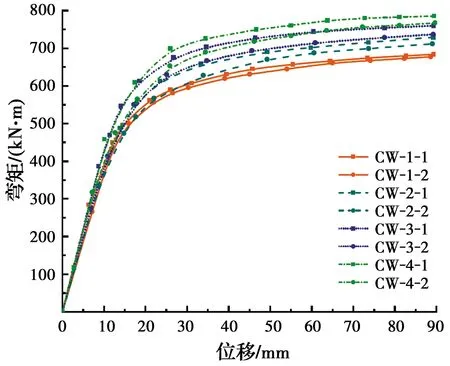
图8 弯矩-跨中挠度曲线Fig.8 Momentmid-span-deflection

由图8可知，该曲线均包括弹性阶段、弹塑性阶段以及塑性强化阶段。加载初期，试件处于弹性阶段，弯矩与跨中挠度呈线性增加；随着荷载的增大，试件进入弹塑性阶段，曲线斜率变小，刚度下降明显，此时，随着跨中挠度的增加，弯矩增长幅度减小；随后试件进入塑性强化阶段，跨中挠度快速发展，弯矩增长速度进一步减缓。

试件在试验过程中荷载下降时，极限抗弯承载力取最大荷载对应的弯矩值；当试件延性较好、在试验过程中荷载未出现下降时，极限抗弯承载力取钢管受拉区最外边缘应变达到10 000×10-6时所对应的弯矩值[15]。各试件的极限抗弯承载力如表3所示。由表3可知，与内部无任何加劲的试件CW-1相比，内配纵向加劲肋试件CW-2截面含钢率提高了0.3%，极限承载力提高了5.4%；内配格构式钢骨试件CW-3截面含钢率提高了0.6%，极限承载力提高了11.3%；内部同时设置纵向加劲肋和格构式钢骨试件CW-4截面含钢率提高了0.9%，极限承载力提高了16.4%。内配纵向加劲肋或格构式钢骨均会提高试件的抗弯承载力，与试件CW-1相比，试件CW-3截面含钢率提升百分比为试件CW-2的2倍，但试件CW-3承载力提升百分比为试件CW-2的2.2倍。因此，格构式钢骨对试件抗弯承载力的提升更明显。

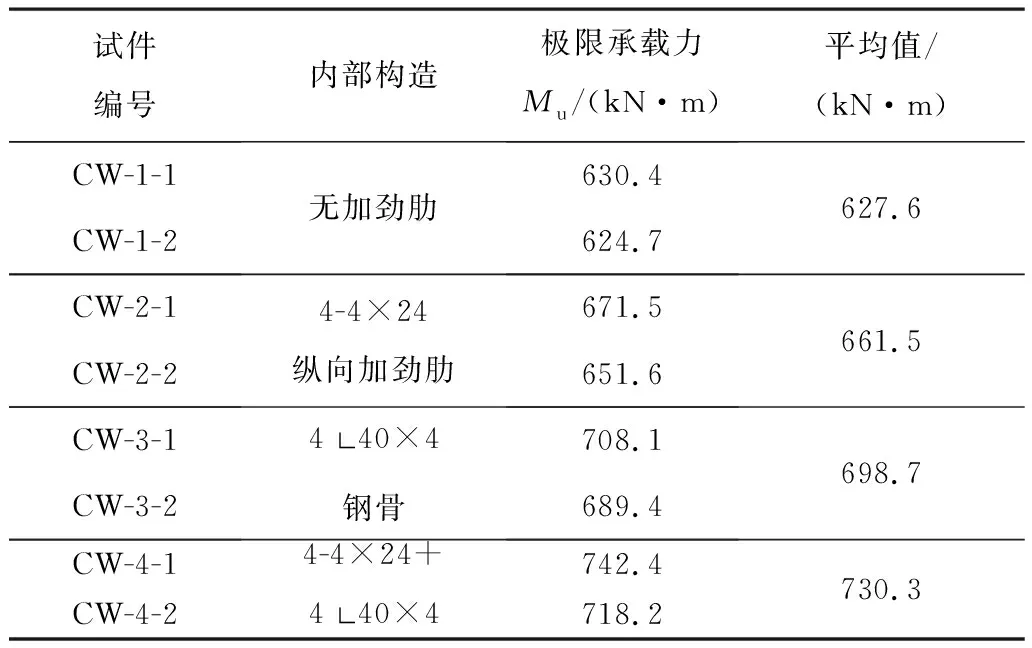
表3 试件极限抗弯承载力

2.3 应变分析

1)平截面验证

图9为各试件弯矩为100～600 kN·m时跨中截面纵向应变分布情况。由图9可知，各试件中和轴高度随荷载的增加沿截面逐渐上升，各级荷载下应变-截面高度曲线基本呈直线，即加载过程中纯弯段跨中截面的应变沿截面高度呈线性变化，应变发展符合平截面假定。

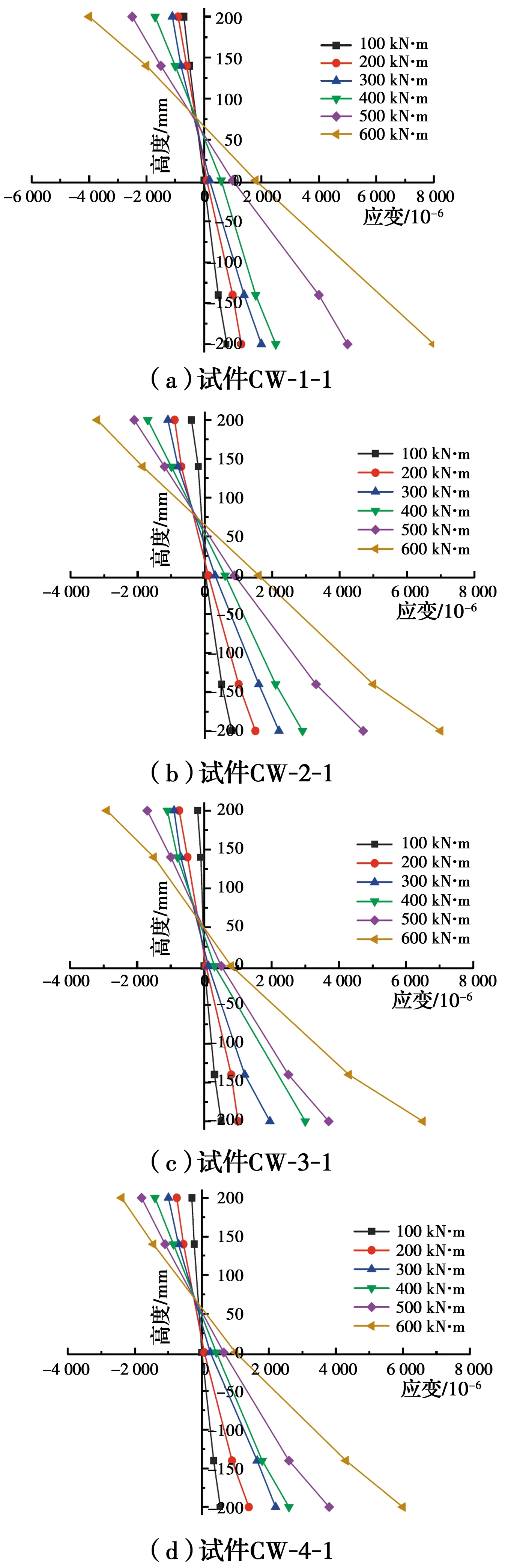
图9 各试件跨中截面纵向应变分布Fig.9 Longitudinal strain distribution of specimen

2)应变发展

试件跨中截面纵向应变发展情况基本一致，如图10所示。加载初期，钢管处于弹性阶段，应变呈线性增长，受拉区应变发展速度大于受压区，受拉区首先进入屈服；随着受拉区钢管的屈服，试件由弹性阶段进入弹塑性阶段，刚度逐渐下降；随后受压区钢管进入屈服，试件进入塑性强化阶段，应变发展加快，试件承载力仍持续增长，但增长速度减慢；加载结束时，所有纵向测点应变均达到屈服应变。

对比各试件应变发展情况可知，所有试件受拉区钢管屈服时所对应的弯矩接近，均为300 kN·m左右，各试件应变发展的主要差别在于受压区钢管屈服时所对应的弯矩。相比于未加劲试件CW-1和带纵向加劲肋试件CW-2，内配格构式钢骨试件CW-3、CW-4的受压区钢管屈服明显延迟。

2.4 抗弯刚度

根据受弯试件跨中截面处曲率与跨中截面最大受拉侧和最大受压侧的应变关系，得到受弯试件跨中截面处曲率φ的计算公式[16]。

(1)

式中：εH3、εH1分别为试件跨中截面下部受拉侧和上部受压侧的纵向应变；D为钢管直径。

由式(1)计算得到试件跨中截面的弯矩-曲率曲线，如图11所示。由图11可知，各试件的弯矩-曲率曲线包括3个阶段：弹性阶段，试件截面中和轴与截面形心轴基本重合，钢材处于弹性阶段；弹塑性阶段，随着荷载增加，中和轴向上部受压区移动，试件下部受拉区扩大，受拉区钢管屈服；塑性强化阶段，随着荷载的进一步增大，受压区钢管屈服，受拉区钢管进入强化阶段，此时试件曲率快速增加，弯矩持续增长，但增长速度减慢。各试件在加载过程中均表现出优异的延性和变形能力。

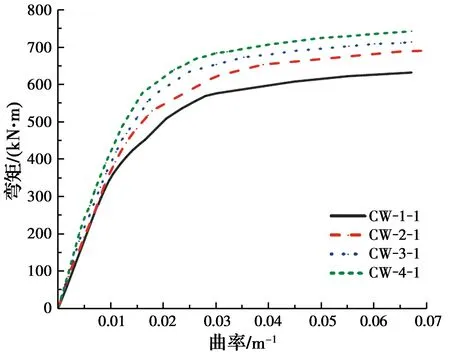
图11 弯矩-曲率曲线Fig.11 Bending moment-curvature

以试件受弯极限承载力试验值的0.2倍所对应的割线刚度作为初始抗弯刚度K0，以受弯极限承载力试验值的0.6倍所对应的割线刚度作为使用阶段的抗弯刚度Ku[15]。各试件不同阶段的抗弯刚度如表4所示，由表4可知：与内部无任何加劲措施的试件CW-1相比，内配纵向加劲肋试件CW-2的初始抗弯刚度提高了5.2%，使用阶段抗弯刚度提高了5.5%；内配格构式钢骨试件CW-3的初始抗弯刚度提高了11%，使用阶段抗弯刚度提高了9.6%；同时设置纵向加劲肋和格构式钢骨的试件CW-4初始抗弯刚度提高了14.9%，使用阶段抗弯刚度提高了14.4%。

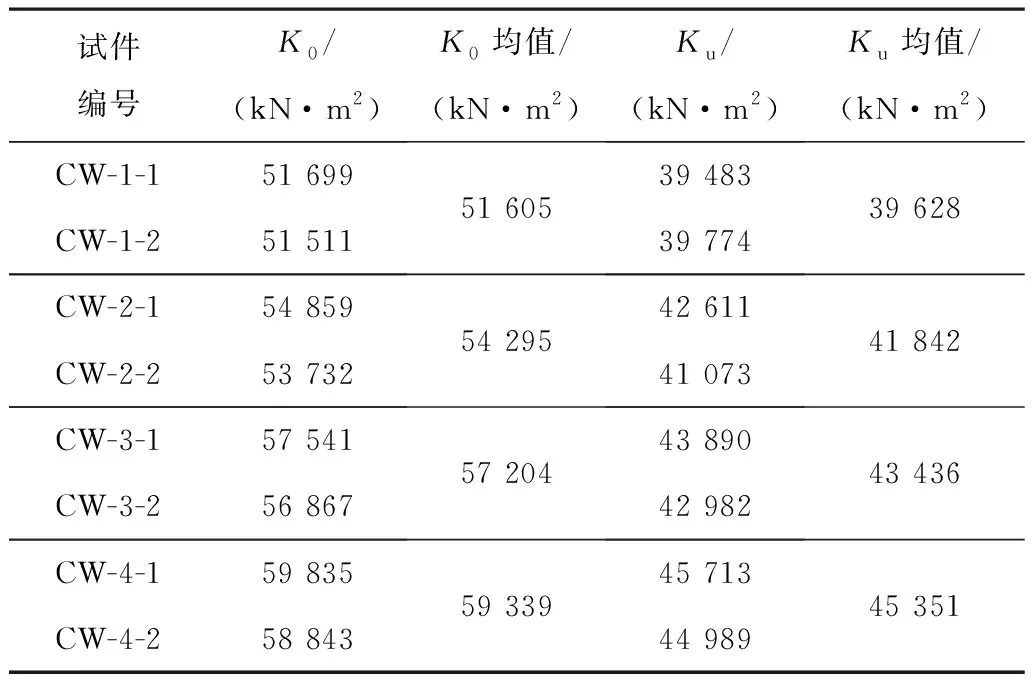
表4 试件抗弯刚度

3 非线性有限元分析

3.1 材料本构模型

采用有限元软件ABAQUS对试件进行数值模拟。钢材采用五折线模型，受压与受拉的应力-应变关系相同[17]。混凝土材料采用损伤塑性模型[18]，泊松比为0.2，膨胀角为30°，双轴受压强度与单轴受压强度之比为1.16，屈服常数为0.666 7。

3.2 有限元模型

纵向加劲肋、钢骨、混凝土及钢管均选用8节点减缩积分实体单元(C3D8R)。钢管和混凝土之间的相互作用采用接触模拟，法向为硬接触，切向为罚摩擦，摩擦系数取0.60[19]。在试件底部距左右两侧150 mm处设置铰接，一侧约束试件沿X、Y、Z方向的平动和绕Y、Z轴的转动，另一侧约束试件沿X、Y方向的平动和绕Y、Z轴的转动，在试件Z轴方向三分点处施加沿Y轴负方向的竖向位移荷载，试件有限元模型如图12所示。

图12 有限元模型

3.3 有限元模拟结果与试验结果对比

有限元与试验破坏形态、荷载-位移曲线对比如图13、图14所示。由图可知，二者破坏形态基本一致，有限元与试验弯矩-位移曲线吻合较好，二者承载力接近，初始刚度略有差异，其原因为有限元分析中加载方式和边界条件均为理想状态，而试验过程中存在接触间隙和加载误差等导致试验初始刚度略低于有限元模拟结果。总体上，有限元分析能较好地反映试件的受力过程。

图13 有限元模拟与试验破坏形态对比Fig.13 Comparison of failure mode between FEM and

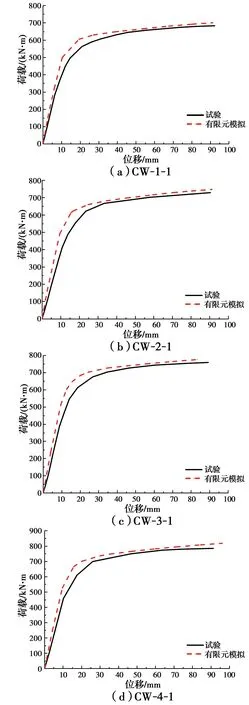
图14 有限元模拟与试验弯矩-位移曲线对比Fig.14 Comparison of bending moment-displacement curves between FEM and

3.4 应力发展过程

Mises准则是用于判断材料是否屈服的应力准则，该准则一般用于判断延性较好的材料，因此，在有限元模拟内配格构式钢骨钢管混凝土构件时，钢管、加劲肋和格构式钢骨的应力状态由Mises应力反映。对于脆性材料，一般采用第一强度理论，认为材料破坏的主要原因是最大拉应力达到允许应力，因此，在有限元模拟内配格构式钢骨钢管构件时，混凝土的应力状态由其沿轴线方向的应力(即S33)反映。

图15为外钢管设置纵向加劲肋、同时内配格构式钢骨试件CW-4的应力发展过程。加载初期，试件处于弹性阶段，钢管与混凝土共同工作，随着荷载的增加，受拉区外侧混凝土开裂并不断向上延伸，试件中和轴上移，下部钢管承受较大的拉力；当受拉区钢管跨中进入屈服时(图15(a))，试件进入弹塑性阶段，钢管塑性区逐渐扩展，受拉区钢骨开始屈服(图15(b))，此时受压区外侧混凝土达到抗压强度(图15(c))；随着荷载的继续增加，受压区最外侧钢管也逐渐屈服(图15(d))，受压区钢骨应力增大(图

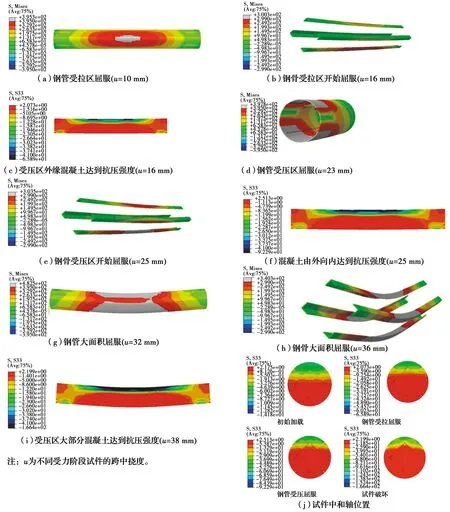
图15 试件应力发展过程Fig.15 Stress development process of

15(e))，混凝土塑性区由外向内扩展(图15(f))，试件进入塑性强化阶段，荷载增长速度明显减缓。随着纯弯段钢管大面积屈服(图15(g))、钢骨受压屈服(图15(h))、大部分混凝土达到抗压强度(图15(i))。加载过程中试件中和轴不断上升，由直线变为曲线(图15(j))。

4 参数分析

为全面了解内配格构式钢骨钢管混凝土受弯构件的力学性能，以试验试件为基本模型，采用有限元方法分析钢管径厚比、钢骨肢件间距、钢骨尺寸、钢骨及混凝土强度对内配格构式钢骨钢管混凝土构件受弯性能的影响。

4.1 钢管径厚比

图16为外钢管径厚比分别为80、67、57的内配格构式钢骨钢管混凝土构件的弯矩-位移曲线。由图可知：各构件均表现出良好的延性；随着外钢管径厚比减小，构件承载力显著增大，其原因为：钢管混凝土构件受弯时，由于混凝土抗拉能力差，受拉区混凝土很快出现裂缝退出工作，试件中和轴不断上升，混凝土受压区面积减小，钢管是承受弯曲荷载的主要受力部件。因此，外钢管径厚比减小，构件含钢率提高，其承载力明显增大。

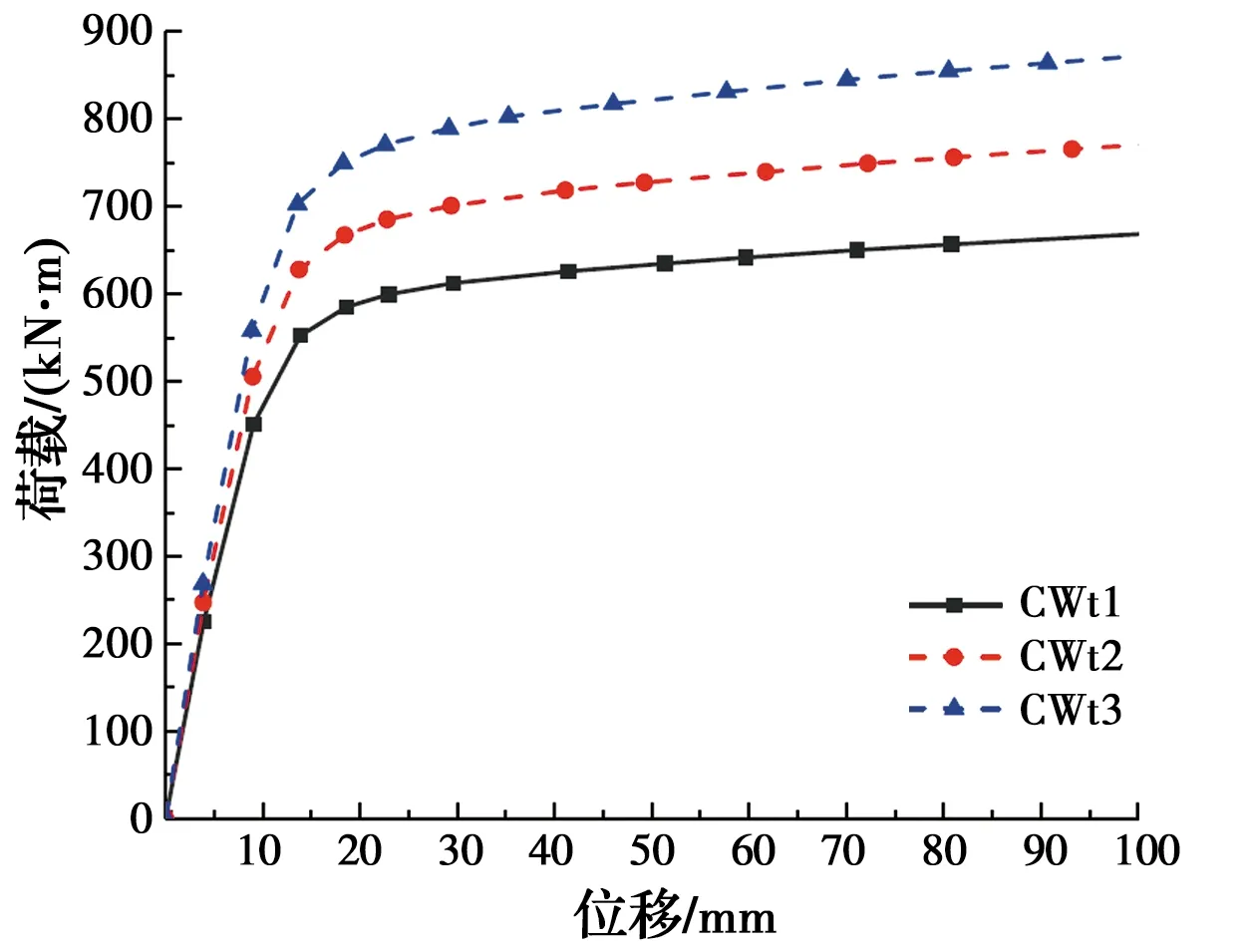
图16 不同钢管径厚比构件的弯矩-位移曲线Fig.16 Bending moment-displacement curves of members with different diameter-thickness ratios of steel

4.2 钢骨尺寸

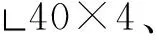
图17 不同钢骨尺寸构件的弯矩-位移曲线Fig.17 Bending moment-displacement curves of members with different steel-reinforced

4.3 钢骨肢件间距

图18为钢骨肢件间距分别为160、180、200、220、240 mm的内配格构式钢骨钢管混凝土构件的弯矩-位移曲线。由图可知，随着钢骨肢件间距增大，内配格构式钢骨钢管混凝土构件的承载力略有提升。其主要原因为随着钢骨间距的增大，自身抗弯抵抗矩越大，则钢骨本身抗弯强度越大，但对于整个截面，钢骨所承担的荷载较小，其主要作用是约束核心混凝土，延缓构件在受力过程中中和轴的上移，因此，在一定范围内改变其肢件间距，对构件的抗弯承载力影响较小。

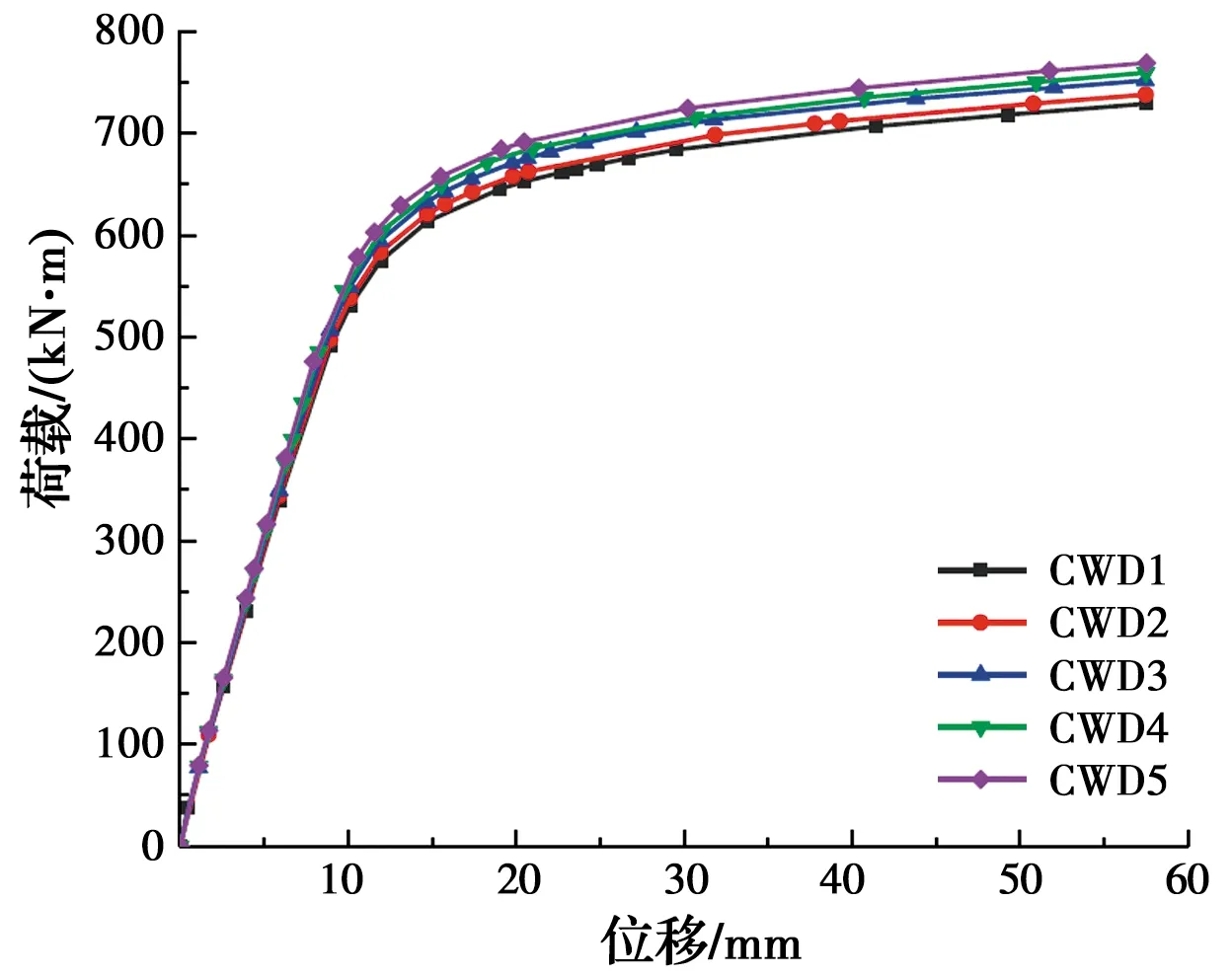
图18 不同钢骨肢件间距构件的弯矩-位移曲线Fig.18 Bending moment-displacement curves of members with different steel limb spacing of

4.4 钢骨强度等级

图19为钢骨强度等级分别为Q235、Q345、Q420的内配格构式钢骨钢管混凝土构件的弯矩-位移曲线。由图可知，随着钢骨强度的提高，构件的抗弯承载力仅有小幅提升。这是由于虽然格构式钢骨强度提高，但钢骨在受弯过程中并未屈服，且对整个构件截面来说，格构式钢骨的总用钢量相对较少，因此，改变钢骨强度对构件受弯性能影响较小。

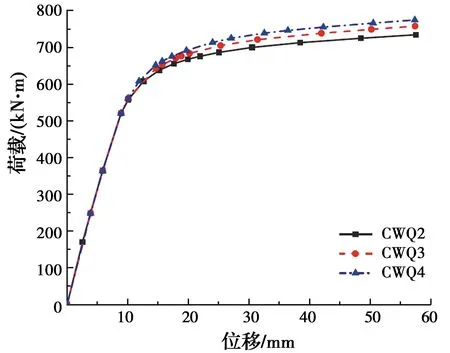
图19 不同钢骨强度构件的弯矩-位移曲线Fig.19 Bending moment-displacement curves of members with different steel-reinforced

4.5 混凝土强度等级

图20为混凝土强度等级分别为C30、C45、C60的内配格构式钢骨钢管混凝土构件的弯矩-位移曲线。由图20可知，随着混凝土强度等级的提高，构件抗弯承载力略有增长。混凝土强度等级对构件抗弯承载力影响较小，这是由于构件受弯时参与受压的混凝土较少，混凝土的主要作用是支撑钢管，防止其受弯屈曲。

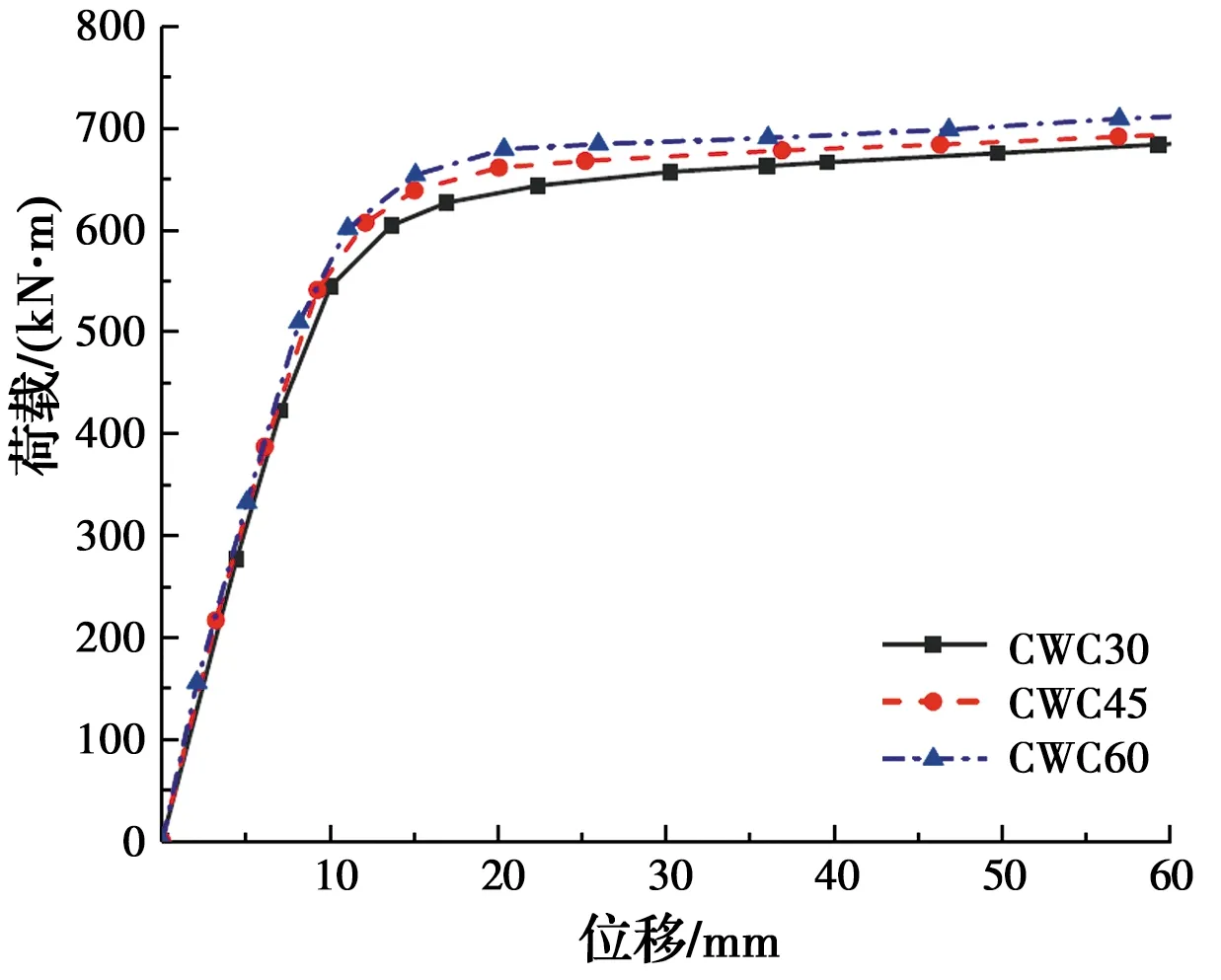
图20 不同混凝土强度构件的弯矩-位移曲线Fig.20 Bending moment-displacement curves of members with different concrete

5 承载力与刚度计算

5.1 承载力计算

对于内配格构式钢骨及纵向加劲肋的钢管混凝土构件，《特殊钢管混凝土构件设计规程》(CECS 408:2015)[20]规定其抗弯承载力Mu1为素钢管混凝土构件与格构式钢骨(及纵向加劲肋)的抗弯承载力之和。

Mu1=M01+Mb

(2)

式中：M01为素混凝土抗弯承载力；Mb为格构式钢骨抗弯承载力。

规范计算值Mu1与试验值Mu对比如表5所示。对于普通钢管混凝土试件，规范计算值与试验值吻合较好；但对于带加劲件的试件，计算结果偏于保守，特别是对CW-4试件，其偏差接近12%。分析其原因，该公式仅为内配件抗弯承载力与钢管混凝土抗弯承载力的简单叠加，未考虑到两者的相互作用能提高试件的整体抗弯承载力。

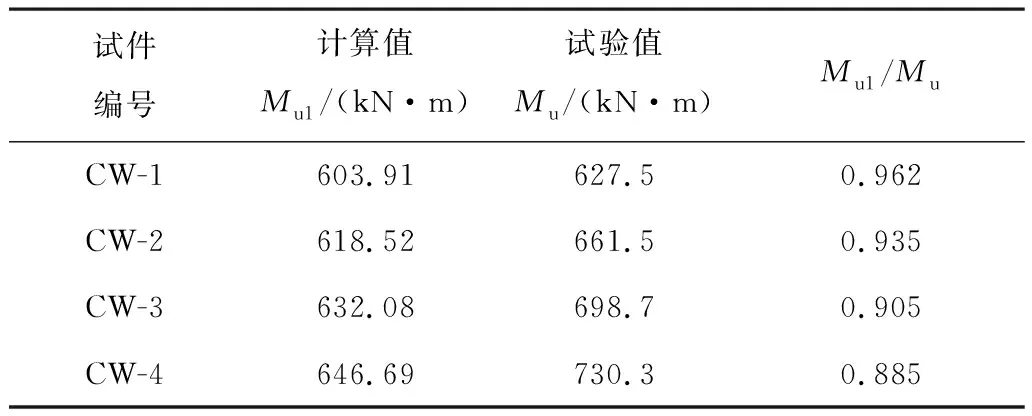
表5 抗弯承载力计算值与试验值对比

5.2 刚度计算

《特殊钢管混凝土构件设计规程》(CECS 408：2015)、美国规范AISC 360-16[21]和欧洲规范EC 4[22]中内配格构式钢骨钢管混凝土构件抗弯刚度的计算公式分别为式(3)～式(5)。

EI=EsoIso+EcIc+EsiIsi

(3)

EI=EsoIso+C3EcIc+EsiIsi

(4)

EI=EsoIso+0.6EcIc+EsiIsi

(5)

将试验所得初始抗弯刚度K0和使用阶段抗弯刚度Ku分别与《特殊钢管混凝土构件设计规程》(CECS 408：2015)、美国规范AISC 360-16和欧洲规范EC 4公式计算值进行对比，如表6所示。

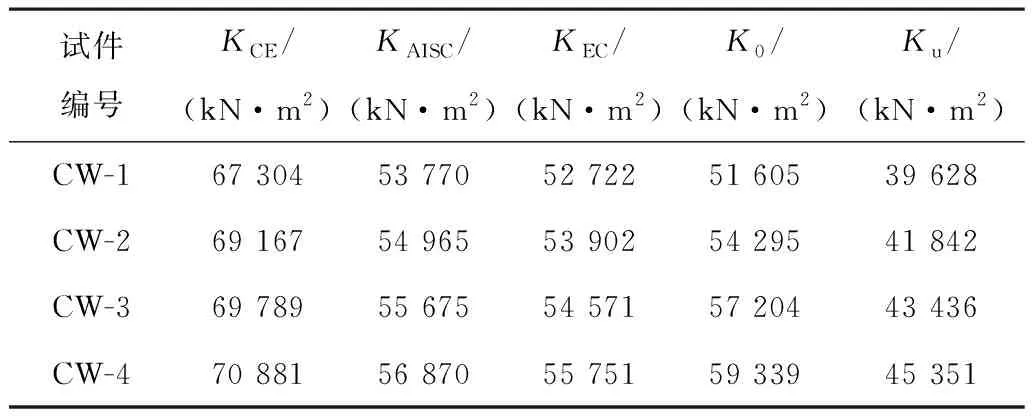
表6 抗弯刚度计算值与试验值对比

由于混凝土抗拉性能较差，构件受拉区混凝土在加载初期即出现开裂，导致截面中和轴上移，参与受压的混凝土面积减小，所以对于构件整体抗弯刚度的贡献较低，在对构件刚度进行计算时，应对混凝土刚度进行相应折减。由式(3)～式(5)可知，各规范对于内配格构式钢骨钢管混凝土构件抗弯刚度的计算均为钢管、核心混凝土、格构式钢骨抗弯刚度的叠加，3种规范的主要区别在于核心混凝土对构件抗弯刚度的贡献大小，《特殊钢管混凝土构件设计规程》(CECS 408：2015)未对核心混凝土刚度进行折减，美国规范AISC 360-16和欧洲规范EC 4规范对核心混凝土抗弯刚度折减的方式类似，只是折减系数不同。从计算结果对比可知，采用美国AISC 360-16规范、欧洲规范EC 4得到的抗弯刚度计算值与试验值最接近，对于普通钢管混凝土构件的刚度计算结果大于试验结果，对于内配加劲件(纵向加劲肋、格构式钢骨)的钢管混凝土构件，刚度计算结果略小于试验结果，偏于安全。采用《特殊钢管混凝土构件设计规程》(CECS 408:2015)的刚度计算值明显大于试验值。

6 结论

对4组不同内部加劲形式的钢管混凝土试件进行受弯试验，通过有限元数值模拟和理论分析，得出以下结论：

1)与内部无任何加劲措施的试件相比，纵向加劲肋使试件截面含钢率增大了0.3%，承载力提升了5.4%；格构式钢骨使试件截面含钢率增大了0.6%，承载力提升了11.3%；同时设置纵向加劲肋和格构式钢骨使试件截面含钢率增大了0.9%，承载力提升了16.4%。

2)受拉区钢管屈服是试件从弹性阶段进入弹塑性阶段的转折点，受压区钢管屈服后，试件逐渐从弹塑性阶段进入塑性强化阶段。

3)钢管径厚比、钢骨尺寸及钢骨强度对构件抗弯性能影响较大，而混凝土强度、钢骨肢件间距对其抗弯性能影响较小。

4)中国规范对于格构式钢骨钢管混凝土构件承载力的计算偏于保守。采用美国和欧洲规范计算的构件刚度值与试验值接近，采用中国规范计算的构件刚度值明显大于试验值。