锈蚀钢筋横截面积分布规律统计分析

刘浩，巴光忠，苗吉军，刘才玮

(1. 青岛理工大学 土木工程学院，山东 青岛 266033；2. 上海海事大学 海洋科学与工程学院，上海 201306)

在混凝土结构使用期间，其内部的钢筋往往因碳化作用或氯离子侵蚀而发生锈蚀，钢筋锈蚀导致结构性能劣化，危及钢筋混凝土结构的安全和使用性能[1]。如何预测混凝土中钢筋的锈蚀程度是混凝土结构耐久性研究领域一直探讨的课题。相较于电化学方法[2]，目视检查在现场检测评估结构性能退化时更加简便易行，因此，许多学者研究了混凝土构件的锈胀裂缝宽度与锈蚀钢筋质量损失之间的相关性[3-4]，而钢筋锈蚀引起的质量损失与截面损失之间的关系也受到了关注[5]。但钢筋的锈蚀是不均匀且随机的[6]，锈蚀过程中经常会发现点蚀的存在，局部蚀坑减少了钢筋的横截面积，导致蚀坑部位出现应力集中[7]，进而使得钢筋强度下降[8]，变形能力减弱[9]。受力过程中，锈蚀钢筋往往在最小截面处失效[10]，因此，关于锈蚀钢筋最小截面积的研究至关重要。然而，锈坑具有随机且不规则的特性，很难获取准确的残余横截面积。传统的量测锈蚀钢筋表面形貌的方法有游标卡尺方法、排水法、X射线与图像处理方法。其中，游标卡尺方法[11]通过测量锈蚀钢筋的直径损失来近似描述钢筋的横截面积损失，但如果锈坑又深又窄，则存在测量困难且难以保证精度的问题；排水法[12]是将锈蚀钢筋注入盛满水的容器中，通过排除水的质量来计算锈蚀钢筋的体积，此方法可以计算钢筋锈蚀后的平均横截面积，但无法得出最小横截面积；X射线与图像处理技术[13]也被用于量化钢筋腐蚀的空间变异性，但当忽略凹坑的形状时，仅能检测到钢筋的剩余半径。最近，三维激光扫描[5]方法被应用于锈蚀钢筋的检测，与以上传统方法相比，在确定腐蚀坑的深度和形状方面被证明更加精确。考虑到上述检测的困难性，笔者采用三维激光扫描的方法获得钢筋锈蚀后的表面形貌。

目前，许多学者[9,14]对锈蚀钢筋的非均匀锈蚀特征参数，如最大截面锈蚀率、最小剩余截面积、点蚀因子RP等，对钢筋力学性能的影响做了大量研究，但在对最大截面锈蚀率、锈蚀不均匀系数等非均匀锈蚀特征参数与质量锈蚀率、平均截面锈蚀率等均匀锈蚀特征参数的相关性研究上，一般只对二者的关系进行简单线性回归[15]，缺少相应的残差检验以及不均匀系数的概率分布分析。此外，最小截面积还可以用锈蚀不均匀系数R来表征，R具有不考虑腐蚀形貌且比RP表征最小截面积时更加直接准确的优点[16]。

虽然较小的样本量很难进行高精度的拟合，但极值统计经常用于分析坑蚀现象。例如，Sheikh等[17]用极值统计方法预测了管道表面的最大坑深分布规律，Stewart[18]用Gumbel分布模拟了钢筋的最大锈蚀深度，Zhang等[16,19]用Gumbel分布描述了锈蚀钢筋横截面积沿长度方向的概率分布。然而，在小样本量的条件下，相较于含有两个分布参数的Gumbel分布，含有3个分布参数的广义极值分布(GEV分布)对锈蚀钢筋横截面积具有更高的拟合精度[20-21]，因为GEV分布统一了包括Gumbel分布在内的3种极值分布函数，可以有效缓解单一极值分布的局限性[22]。

为深入分析锈蚀钢筋横截面积的分布规律，笔者先在实验室通过电化学加速锈蚀的方法获得不同锈蚀程度的钢筋，然后利用三维激光扫描技术对不同锈蚀程度的钢筋进行实体建模，提取锈蚀钢筋的横截面积。采用统计方法建立非均匀锈蚀特征参数与平均截面锈蚀率之间的关系，并分析锈蚀不均匀系数R的概率分布，确定R的分布参数与其平均截面锈蚀率的关系，此外，还讨论了单元长度和钢筋直径对R分布参数的影响，为混凝土结构的耐久性分析提供依据。

1 材料与方法

1.1 试件设计与制备

选用工程中常用的钢筋来研究其在混凝土中发生锈蚀后的横截面积分布规律，钢筋的类型如表1所示。共制作了96个锈蚀钢筋和4个未锈蚀钢筋试样。为了模拟工程中钢筋的实际锈蚀状态，将钢筋埋在混凝土板中进行加速锈蚀。混凝土板的设计尺寸为374 mm×400 mm×100 mm，板中钢筋单排单向布置，每排6根，保护层厚度为30 mm，采用C30混凝土浇筑。为使钢筋加速锈蚀，在混凝土搅拌过程中加入占水泥重量3%的NaCl。试验中仅使埋在混凝土板中的300 mm钢筋发生锈蚀，混凝土板的尺寸与钢筋位置如图1所示。共设计并制作了16块混凝土板，得到96根不同锈蚀程度的钢筋。

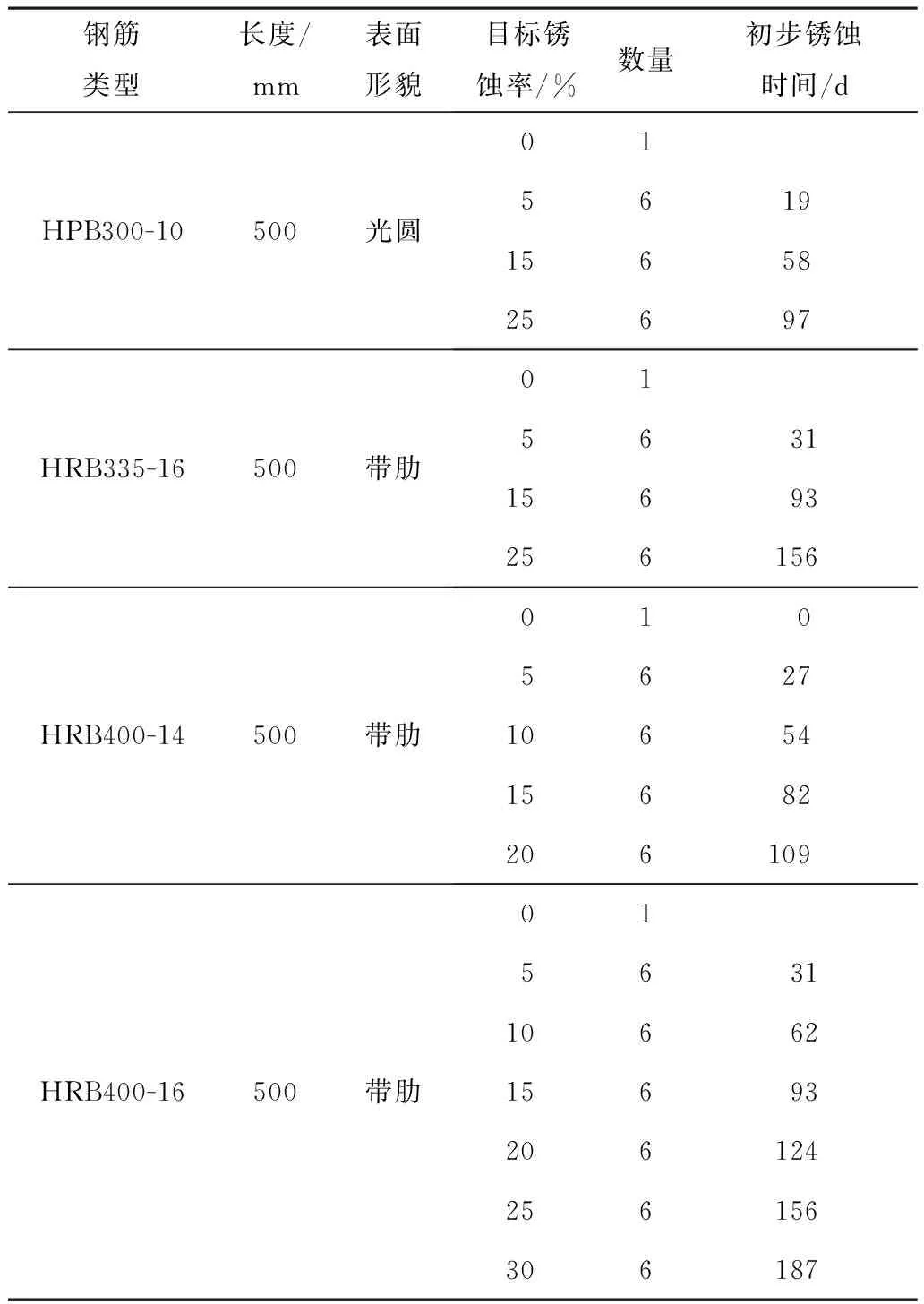
表1 钢筋概况及初步锈蚀时间

试件设计的目标锈蚀率对应实际锈蚀试验中的质量锈蚀率，其计算公式见式(1)。

(1)

式中：ηs为质量锈蚀率，%；m0为锈蚀前钢筋质量，g；m为锈蚀后钢筋质量，g。

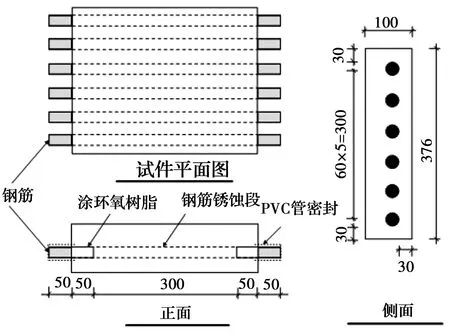
图1 混凝土板的尺寸与钢筋布置Fig.1 Size and reinforcement arrangement of concrete

1.2 加速锈蚀试验

采用电化学加速锈蚀的方法获得不同锈蚀程度的钢筋。将养护完成后的混凝土板放入装有浓度约5%的NaCl溶液的塑料容器中，控制溶液水平面不越过钢筋底面，以保证钢筋与空气充分接触。为使加速锈蚀试验结果尽量接近自然锈蚀状态，电流密度取200 μA/cm2，电化学加速锈蚀试验装置示意图见图2。用电线将直流稳压稳流电源与钢筋上焊接的电线相连，其正极与钢筋相连，负极与铜片相连。根据法拉第定律，可以得到目标锈蚀率和通电时间的关系，如表1所示。当通电时间达到预定值后，关闭电源，拆除钢筋上的电线，将混凝土板从溶液中取出，对板进行破形，取出混凝土中的钢筋。按照《普通混凝土长期性能和耐久性能试验方法标准》(GB/T 50082—2009)[23]清除钢筋表面的锈蚀产物和混凝土，采用12%盐酸溶液对锈蚀钢筋进行酸洗，经清水漂净后，用石灰水中和，再以清水冲洗干净，将钢筋试样放入干燥器中存放4 h后取出，得到的锈蚀钢筋如图3所示。用电子天平(精确至0.001 g)称取锈蚀钢筋的质量，根据钢筋锈蚀后的质量，计算其实际质量锈蚀率。

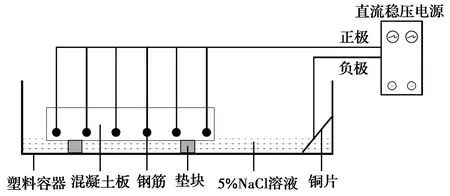
图2 电化学加速锈蚀装置示意图Fig.2 Schematic diagram of electrochemical accelerated

图3 通过加速锈蚀试验得到的锈蚀钢筋Fig.3 Corroded steel bars obtained by accelerated

1.3 锈蚀钢筋的几何特征提取

选用三维激光扫描技术提取锈蚀钢筋的几何特征参数，利用三维扫描仪对锈蚀钢筋逐一进行三维扫描，扫描现场如图4(a)所示。通过扫描试验获取锈蚀钢筋的点云数据，利用点云数据重构锈蚀钢筋的三维几何模型，具体步骤如下：

1)利用三维激光扫描仪扫描锈蚀钢筋，由CMOS摄像机采集被扫描钢筋表面的光刀曲线，然后通过计算机处理，最终得到锈蚀钢筋的三维几何数据，即大量的点云数据。

2)运用Geomagic Studio软件，对点云数据进行优化处理，包括去除锈蚀钢筋模型以外的点云数据、进行滤波处理和噪音去除等，从而提高数据的信噪比，获取更加真实的点云数据。然后对点云数据进行网格化处理和快速曲面构建。最后通过缝合功能把封闭的锈蚀钢筋曲面转化为锈蚀钢筋三维几何模型，如图4(b)所示。从图中可以看出，锈蚀钢筋的三维几何模型与实际钢筋的锈蚀形态吻合良好。

3)将得到的三维几何模型导入参数化软件Pro/Engineer，沿钢筋长度方向以1 mm的间隔垂直切割钢筋，得到锈蚀钢筋的横截面形状及间隔1 mm的横截面积分布。图5为切割得到的锈蚀钢筋横截面形状，图中平均截面锈蚀率为ηave=(As0-Asc)/As0，其中，As0为钢筋锈蚀前横截面积，Asc为钢筋锈蚀后横截面积。

图4 锈蚀钢筋三维激光扫描Fig.4 3D laser scanning of corroded steel

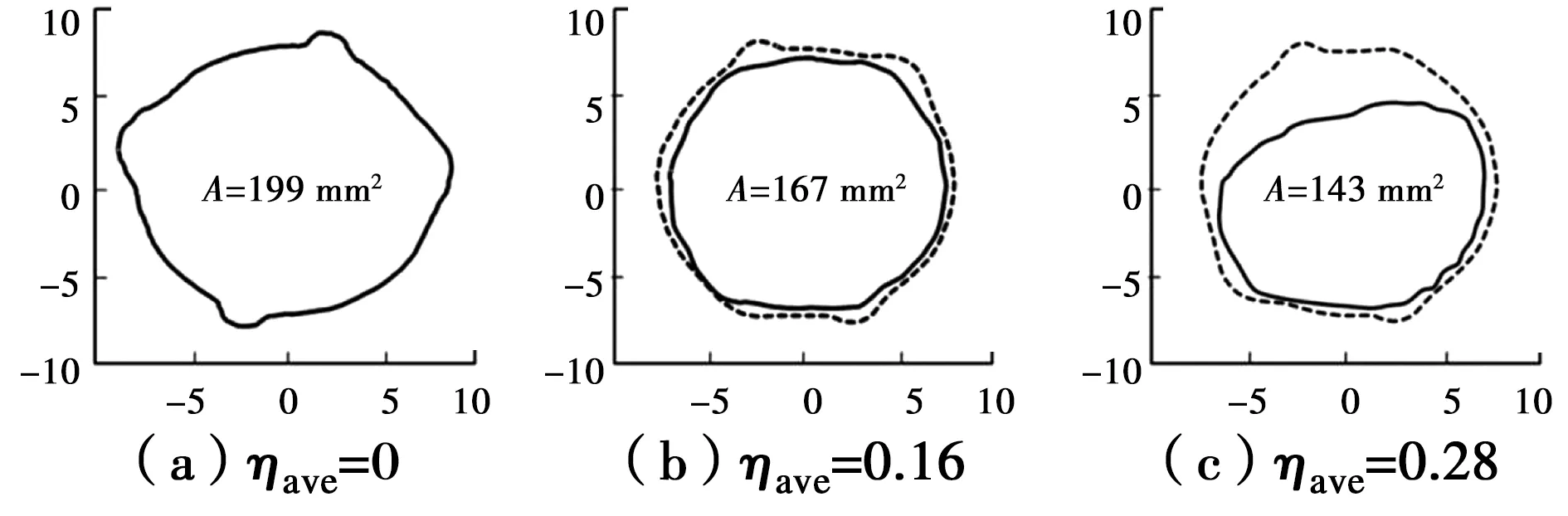
图5 锈蚀钢筋典型截面形式Fig.5 Representative cross sections of corroded steel

2 结果与分析

2.1 横截面积的分布

以直径16 mm的HRB400钢筋为例，对锈蚀钢筋的横截面积进行分析。从图5中可以发现，锈蚀显著减小了横截面积，并且在图4(b)中可以观察到，当锈蚀率不大时，锈蚀相对比较均匀，当锈蚀率较大时，钢筋靠近外部的一侧锈蚀明显更严重。图6是沿钢筋长度方向间隔1 mm的横截面积分布图，图中数字为钢筋的平均截面锈蚀率，从图中可以看出，随着平均截面锈蚀率不断增大，钢筋横截面积在一定范围内波动，最小截面积下降严重，横截面积沿长度方向的不均匀性显著增强。

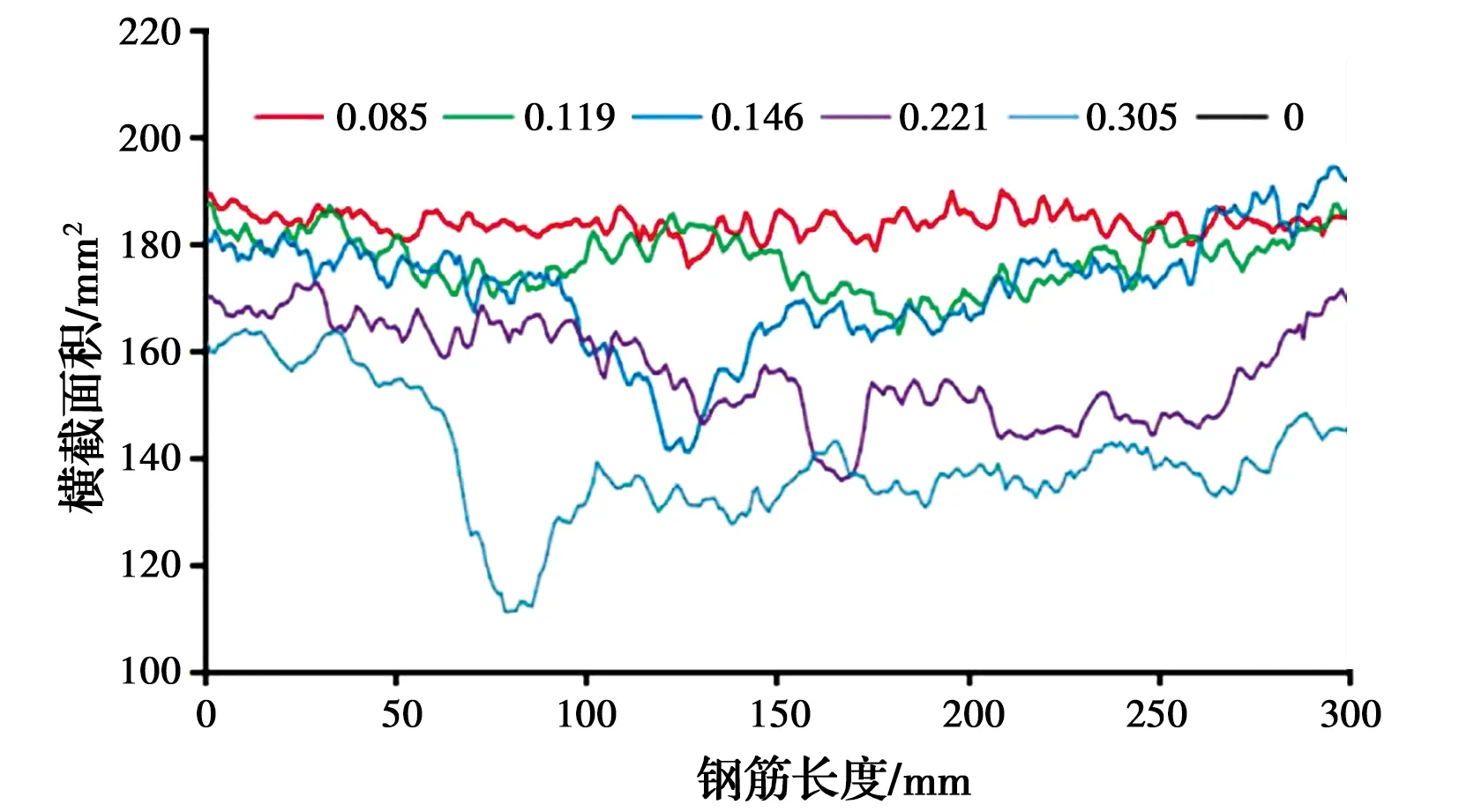
图6 横截面积沿钢筋长度方向的分布Fig.6 Distribution of cross-sectional area along the

2.2 锈蚀特征参数分析

考虑到锈蚀的不均匀性，基于锈蚀钢筋的横截面积统计分析了与锈蚀相关的3个特征参数分布规律，即平均截面锈蚀率ηave、最大截面锈蚀率ηmax和锈蚀不均匀系数R。

(2)

(3)

(4)

式中：As0为未锈蚀钢筋的横截面积，mm2；Asc为钢筋锈蚀段横截面积的平均值，mm2；Asc min为锈蚀钢筋最小横截面积，mm2；R为锈蚀不均匀系数。

由于试验数据有限，为了总结规律，引用了余波等[15]的部分试验数据。

图7为最大截面锈蚀率与平均截面锈蚀率的关系，图中数据为采用普通最小二乘法(OLS)进行回归分析，剔除标准化残差位于区间(-2，2)以外的数据得到的，以此可保证剩余数据具有95%置信度，为非异常值[24]，异常值是由于提取截面积时未能提取到最小截面导致的。通过残差分析来验证解释变量与被解释变量之间的非线性、正态性、同方差性和独立性。从图7可以看出，对于不同类型的钢筋，最大截面锈蚀率均随平均截面锈蚀率的增大而增大，根据三维模型提取到的特征参数值可拟合出钢筋的平均截面锈蚀率与最大截面锈蚀率之间的关系，结果显示，各拟合表达式的可决系数R2均大于0.9，非线性的拟合优度较好。

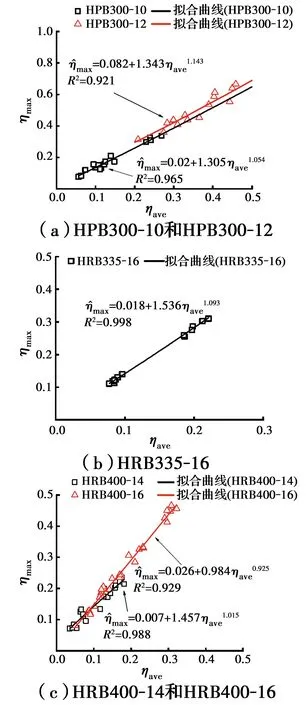
图7 最大截面锈蚀率与平均截面锈蚀率的关系Fig.7 Relationship between maximum cross-sectional loss ratio and average cross-sectional loss

根据拟合表达式，可以得到不同平均截面锈蚀率所对应的最大截面锈蚀率，如表2所示。分别以HPB300和HRB400的锈蚀钢筋为例进行分析，发现直径对锈蚀特征参数有一定的影响，在平均截面锈蚀率相同的情况下，最大截面锈蚀率随直径的增大而增大；另外，在平均截面锈蚀率相同的情况下，光圆钢筋的最大截面锈蚀率要小于带肋钢筋，这不仅受到了直径的影响，还因为光圆钢筋以均匀锈蚀为主，而带肋钢筋以不均匀的局部锈蚀为主[25]，这也意味着当二者的最大截面锈蚀率相同时，光圆钢筋的平均截面锈蚀率要大于带肋钢筋。

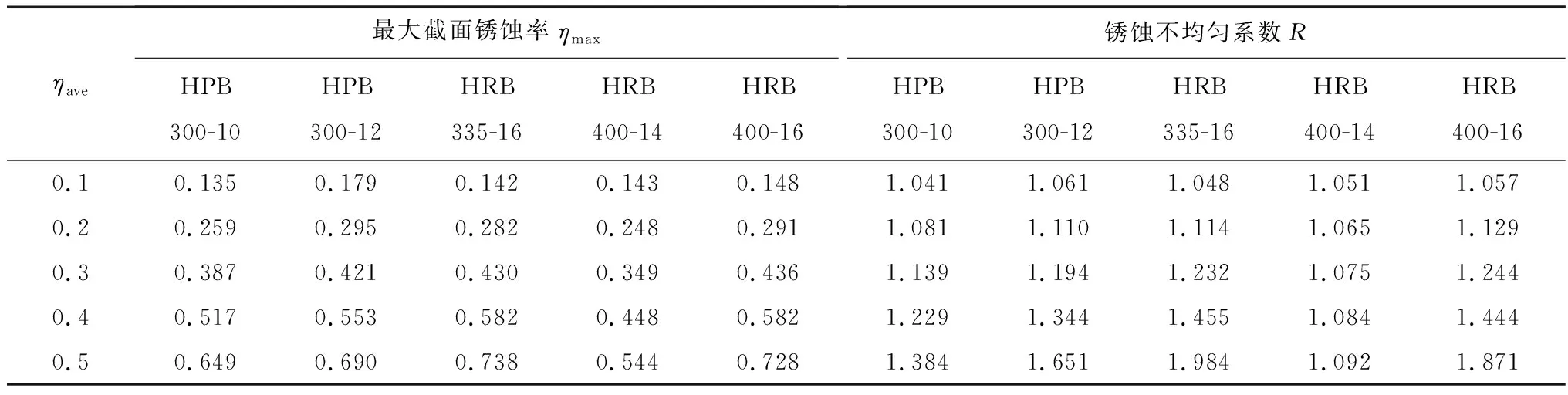
表2 锈蚀特征参数的预测值

通过对最大截面锈蚀率与平均截面锈蚀率关系的回归分析，可以认为二者关系满足公式

(5)

式中：a、b和c为对试验数据进行回归得到的参数。为了便于工程应用，根据图7中的试验数据，对表达式中参数a、b和c进行统计分析，得到考虑钢筋种类和直径影响的参数a、b和c的表达式，如表3所示。

表3 参数a、b和c的表达式

根据式(4)和式(5)，可以得到锈蚀不均匀系数R。

(6)

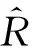
虽然引用了余波等[15]的部分试验数据，但其是通过拍照的方法近似测得锈蚀钢筋的空间形态，不同于三维激光扫描方法。此外，受限于试验数据，关于直径对锈蚀不均匀性影响的研究有待进一步加强。

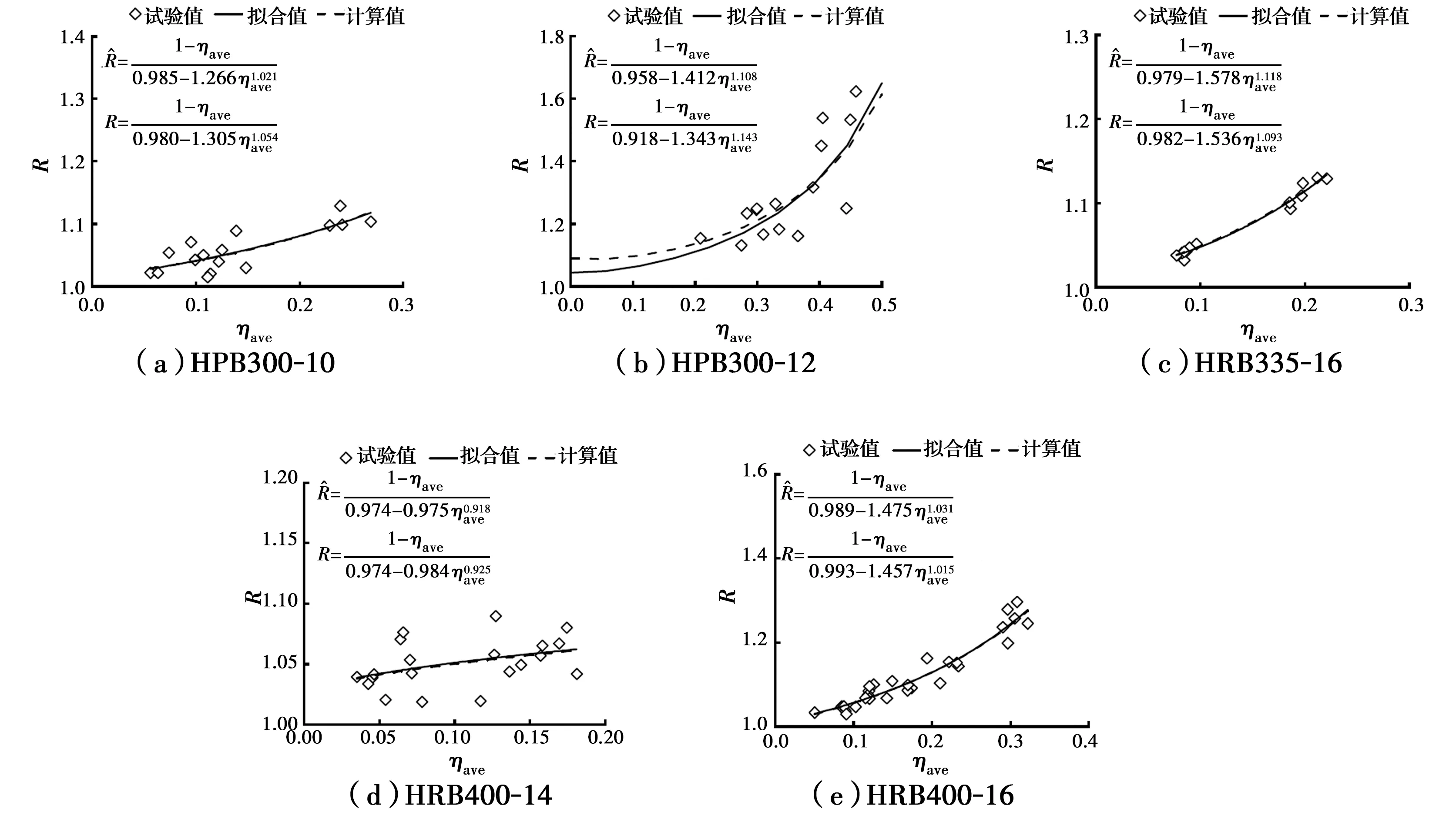
图8 不均匀系数R与平均截面锈蚀率的关系Fig.8 Relationship between non-uniform coefficient R and average cross-sectional loss

图9是图7和图8对应的非线性回归分析后的标准化残差关于拟合值的散点图。从图中可以看出，散点均匀散落在(-2，2)的水平带内且不呈任何趋势，标准化残差图可以显示出任何异常，因此，解释变量与被解释变量之间的非线性假设以及标准化残差的独立性都是可以接受的。另外，为了验证残差的正态性，采用K-S检验、Anderson-Darling检验和C-S检验对标准化残差进行正态性检验，表4列出了它们的统计量和临界值，结果显示，所有标准化残差均接受显著性水平为0.05(95%置信度)的正态性检验。此外，为了验证残差的同方差性，采用white检验对标准化残差进行同方差性检验，表5列出了检验结果，结果显示，所有标准化残差均接受显著性水平为0.05(95%置信度)的同方差性检验。

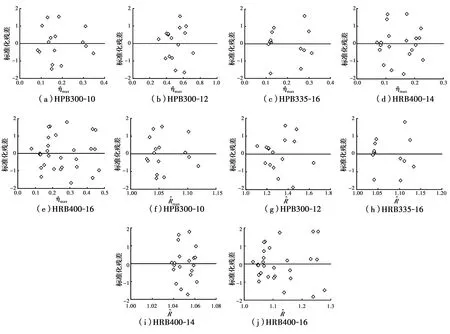
图9 非线性回归分析的标准化残差Fig.9 Standardized residual of nonlinear regression

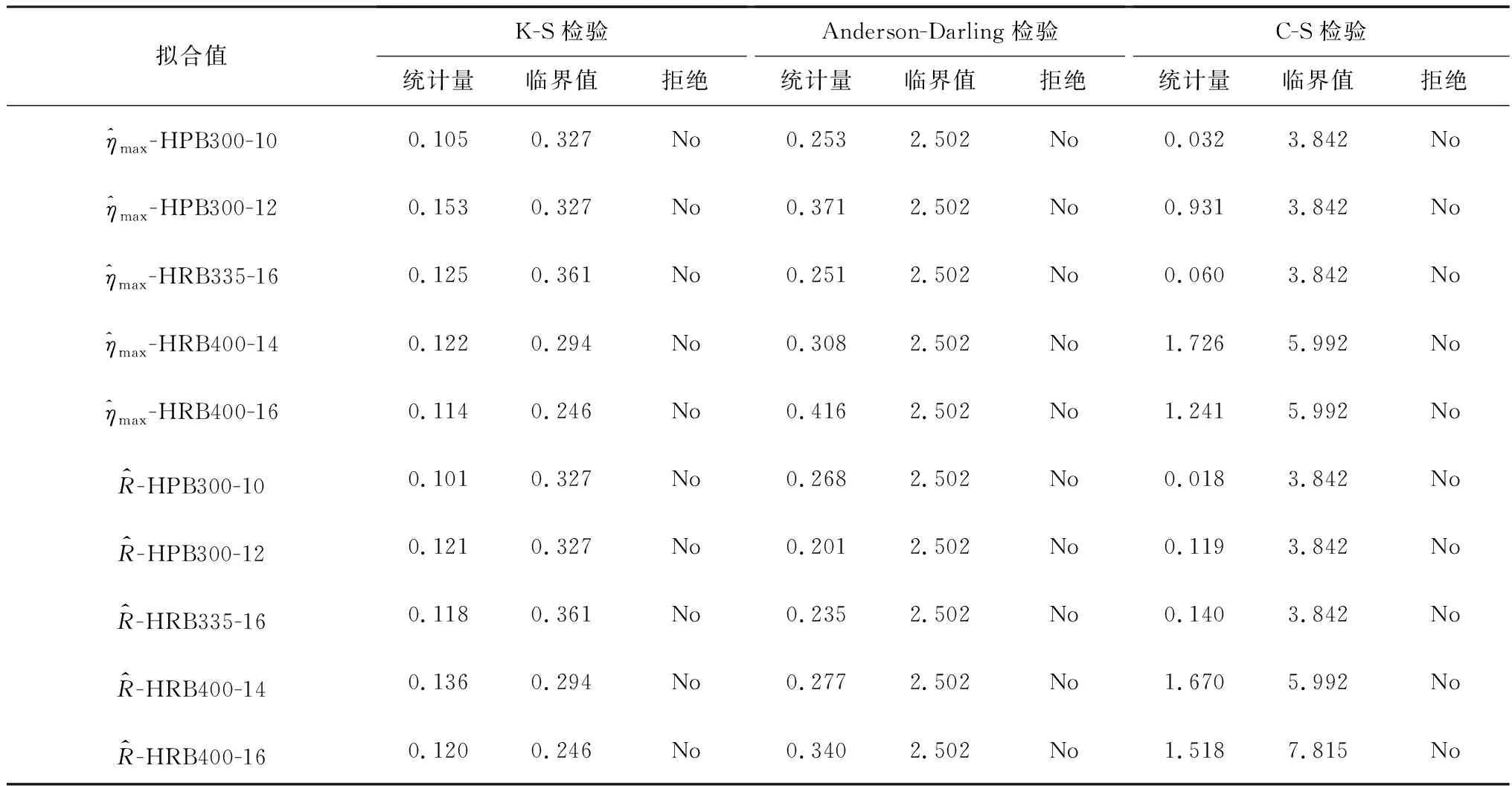
表4 标准化残差的正态性检验

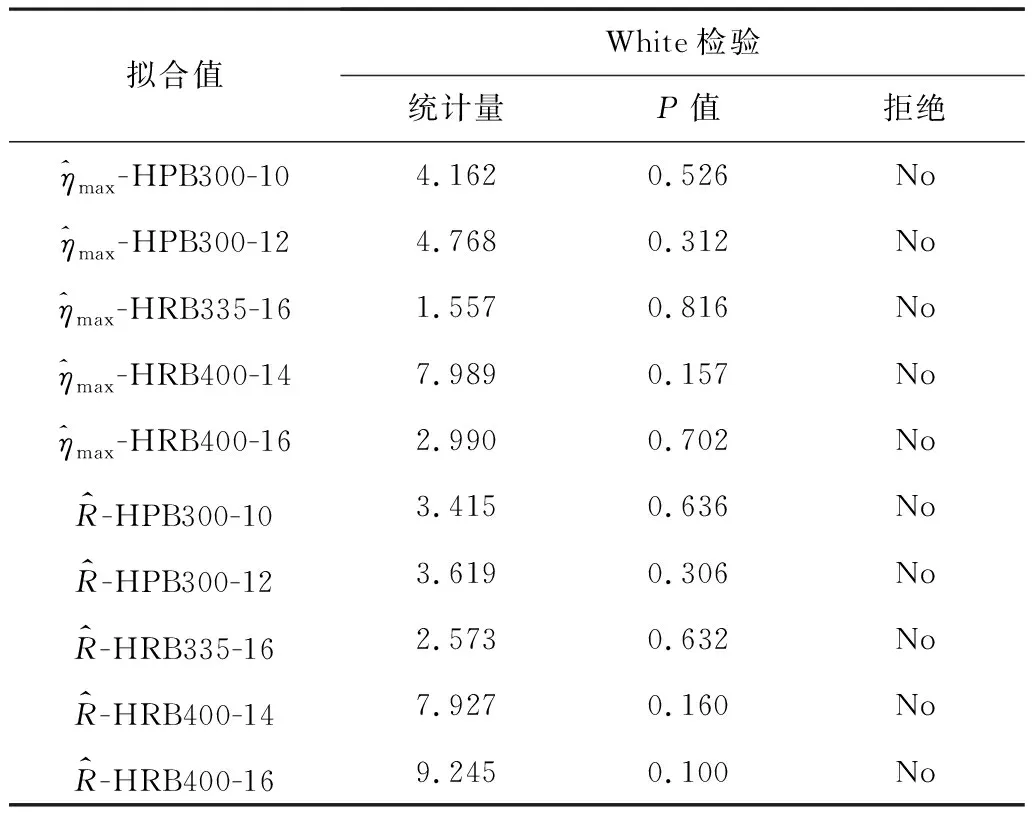
表5 标准化残差的同方差性检验

2.3 R的概率分布模型

Gu等[26]使用自相关函数研究了锈蚀钢筋的单元长度对不均匀系数R的影响，研究表明，在单元长度处于30～50 mm之间时，自相关系数基本上可以保证小于0.3(0.3经常被认为是弱相关系数临界值)，其中小部分不满足的原因可能是自相关系数通过估计自相关函数得到，而估计值只有在样本趋于无穷大时才是无偏估计，这意味着估计结果和实际结果可能存在误差。因此，考虑到每根钢筋的实际统计长度为300 mm，根据参数拟合时的数据量要求以及钢筋实际长度，可将其划分为10个长度为30 mm的等长单元。使用逆累积分布函数(CDF-1)将GEV分布、Gumbel分布、Normal分布和Weibull分布等概率分布拟合到不均匀系数R的数据中，见图10。从图中可以看出，不同条件下的不均匀系数R均能较好地符合GEV分布，因此，选择用GEV分布为锈蚀不均匀系数R建模，且得到的GEV分布形状参数k并不严格趋近于0，所以，用GEV分布来拟合不均匀系数R的概率分布模型是合适的。由于剩余横截面积的平均值是基于整根锈蚀钢筋确定的，而最小值是基于每个单元的，因此有几个不均匀系数R是小于1的。

GEV分布函数F(x)为

(7)

式中：k为形状参数；μ为位置参数；σ为尺度参数。当k=0时，对应极值Ⅰ型(Gumbel)分布，当k>0时，对应极值Ⅱ型(Frechet)分布，当k<0时，对应极值Ⅲ型(Weibull)分布。

表6列出了使用EasyFit软件对不均匀系数R进行概率分布拟合得到的分布参数，另外，对使用Kolmogorov-Smirnov(K-S)检验和Anderson-Darling检验得到的拟合优度检验结果进行对比。结果表明，在显著性水平为0.05(95%置信度)的情况下，所有GEV分布都被两种检验所支持。

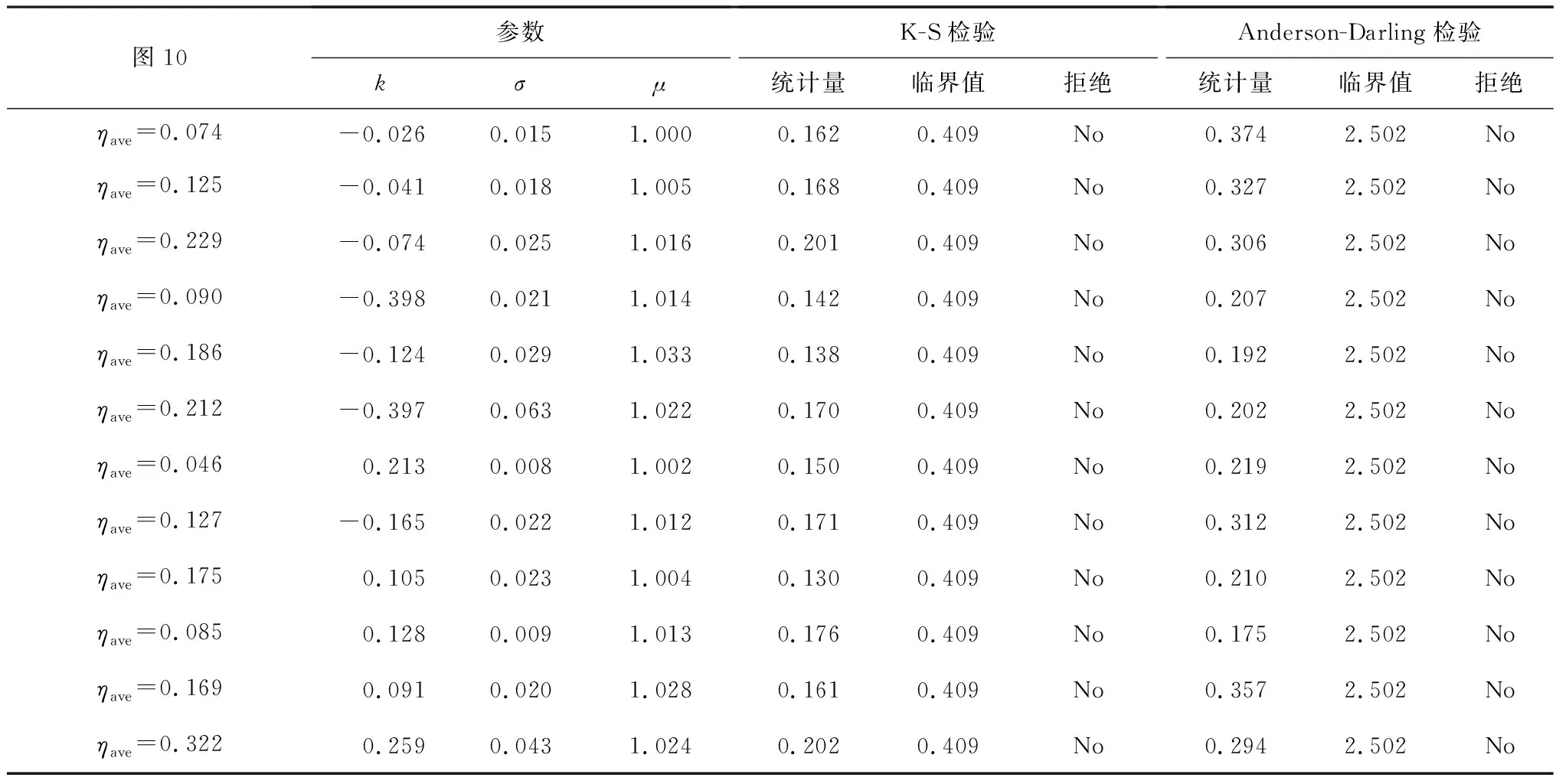
表6 GEV分布的参数估计及拟合优度检验

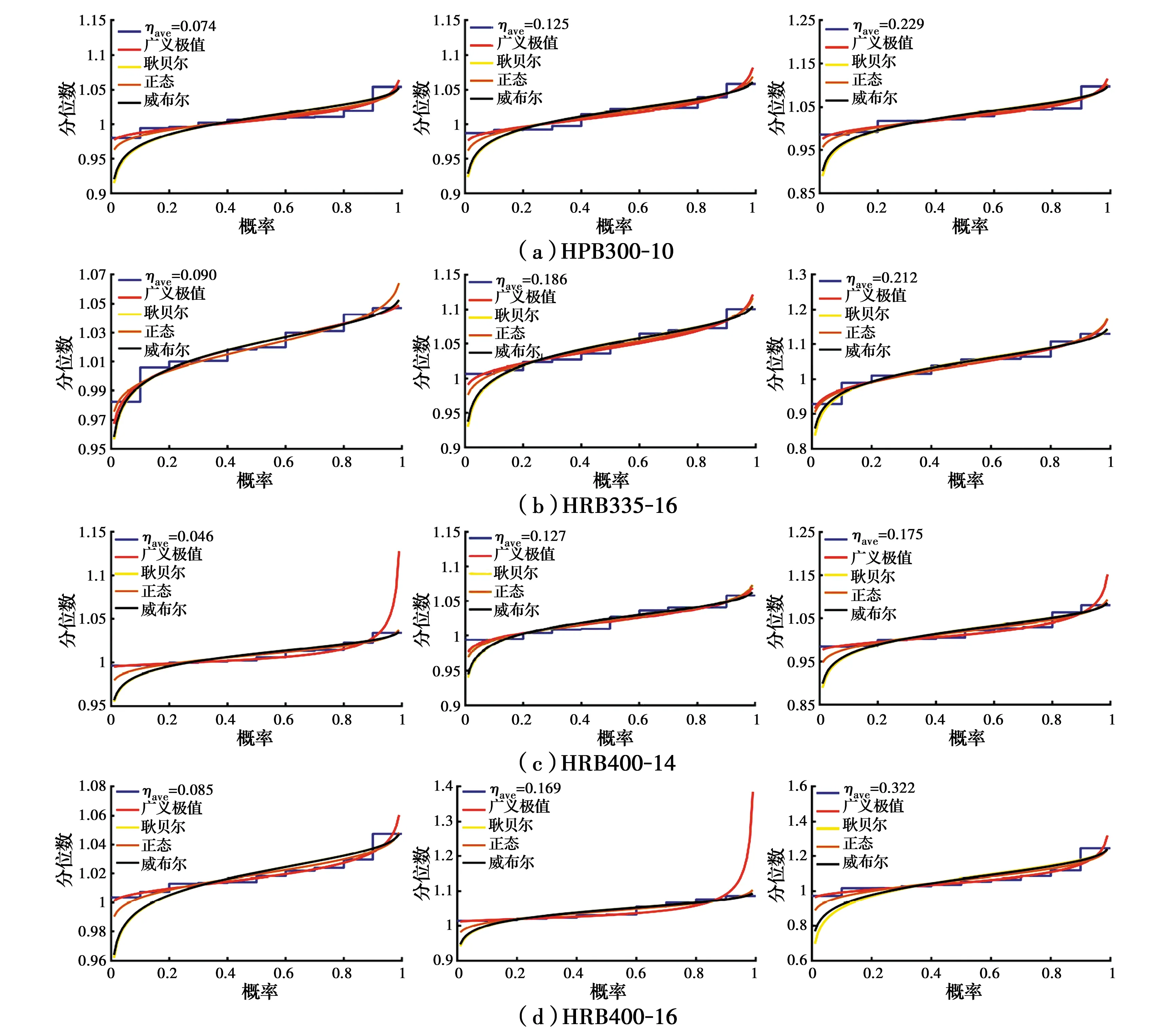
图10 不均匀系数R的逆累积分布函数图Fig.10 CDF-1 diagrams of non-uniform coefficient

另外，已有研究表明，R的概率分布还与锈蚀钢筋的表面积有关[16]，假设所有钢筋单元的表面积是相互独立的，为了预测R随表面积的变化规律，可以将GEV分布参数修改为[16-17]

(8)

(9)

σ=σ0

(10)

式中：k0、μ0和σ0是从表面积为ΔAi的钢筋锈蚀试验中获得的R的GEV分布参数；ΔAi为某一锈蚀钢筋单元的表面积，ΔAi=πDiΔLi；A为锈蚀钢筋的总表面积，A=∑ΔAi；Di和ΔLi分别为第i单元锈蚀钢筋的等效直径和长度。

为了验证式(8)～式(10)，分析了单元长度和钢筋直径对各分布参数的影响，见图11。根据随机场原理[27]，分析长度越短，单元之间的相关性越强，反之亦然，因此，为了保证不均匀系数R是独立的随机变量，并且考虑到概率分布拟合时对数据量的要求以及钢筋实际长度的影响，单元长度选用30、50 mm两种。由图11可以发现，参数k、σ和μ均随平均截面锈蚀率的增大而增大，其中，参数k随平均截面锈蚀率的增大而逐渐趋于正值，即随着锈蚀程度的不断发展，不均匀系数R逐渐倾向于服从Frechet分布。对同一锈蚀钢筋而言，参数k和σ随单元长度的变化不大，可以认为单元长度对参数k和σ没有影响。然而，参数μ随着单元长度的增大而明显增大，这可归因于在统计中使用较大的单元长度减少了非最小截面积出现的频率，相对来说，单元长度越大，越接近真实情况。在单元长度相同的情况下，比较图11(c)、(d)中拟合公式的回归系数可知，参数k随直径的增大而显著减小，这意味着钢筋的直径越小，不均匀系数R随锈蚀程度的发展而越倾向于服从Frechet分布，参数σ和μ则表现出随直径的增大而增大的趋势。

图11 不均匀系数R的GEV分布参数与平均截面锈蚀率的关系Fig.11 Relationship between GEV distribution parameters of non-uniform coefficient R and average cross-sectional loss

3 结论

1)通过对锈蚀钢筋横截面积的统计分析发现，钢筋的最大截面锈蚀率和锈蚀不均匀系数均随着平均截面锈蚀率的增大而增大。另外，在平均截面锈蚀率相同的前提下，最大截面锈蚀率和锈蚀不均匀系数均随着钢筋直径的增大而增大，且锈蚀特征参数的标准化残差均接受显著性水平为0.05的正态性检验和同方差性检验。

2)钢筋单元的锈蚀不均匀系数服从广义极值分布，且分布参数均表现出随平均截面锈蚀率的增大而线性增大的趋势。随着锈蚀程度的不断发展，不均匀系数R逐渐倾向于服从Frechet分布。

3)单元长度对参数k和σ的影响不大。但是随着单元长度的增加，位置参数μ显著增加。对单元长度相同的锈蚀钢筋而言，随着直径的增大，形状参数k显著减小，而尺度参数σ和位置参数μ增大。