基于标贯试验的砂土液化概率判别法

肖诗豪，程小久，汪华安，张洁

(1. 同济大学 地下建筑与工程系；岩土及地下工程教育部重点实验室，上海 200092；2. 中国能源建设集团广东省电力设计研究院，广州 510663)

砂土液化是一种由地震诱发的常见自然灾害，可能会导致砂沸、建筑物地基承载力下降、地表侧移和沉降，进而造成结构破坏和生命财产损失[1-2]。在工程实践中，基于标准贯入试验、静力触探试验和剪切波速试验等原位测试的经验方法在砂土液化判别中获得了广泛的应用。

在中国，基于标贯试验的经验液化判别准则使用最为广泛，如《建筑抗震设计规范》(GB 50011—2010)(2016年版)[3]，以下简称建规法。该方法采用临界标贯击数来衡量地震诱发液化的荷载，采用实测标贯击数来衡量土体抵抗地震液化的能力。当实测标贯击数小于临界标贯击数时，土体发生液化；否则土体不发生液化。建立该方法的关键是提出合理的临界标贯击数计算公式。目前，该公式多通过对中国以往地震震后调查中获得的液化案例库进行分析来获得，因此临界标贯击数计算公式应尽可能区分液化案例库中的液化案例和非液化案例。

Seed等[4]提出的经验判别方法通过不断修正与更新，获得了长足的发展[5-8]。这些简化方法多采用循环应力比(Cyclic Stress Ratio，CSR)来衡量作用在土体上的荷载，采用循环抗力比(Cyclic Resistance Ratio，CRR)来衡量土体抵抗液化的强度。其中，CRR可采用不同的原位测试指标来估算。从理论上讲，CSR>CRR表示土体会发生液化，反之，则不会发生液化。在给定CSR计算方法的条件下，建立经验法的关键是选择合适的CRR计算方法，使得CRR临界曲线尽可能区分案例库中的液化案例和非液化案例。

在建立经验判别准则的过程中存在大量的不确定性因素，导致经验法很难完全区分液化和非液化案例。因此，基于经验法的液化判别结果存在不可忽视的不确定性。液化概率可用于衡量液化发生的可能性[9]，为考虑液化判别结果的不确定性，基于概率的液化判别准则受到了重视。判别分析方法[10-11]、逻辑回归模型[12-17]、人工神经网络[18-21]、结构可靠性方法[22]、贝叶斯方法[7-8,15,23-24]等被广泛用于建立液化势评估的概率模型。Juang等[25]和陈国兴等[26]对土体液化概率判别模型的发展进行了全面的回顾。

由于原理简单、使用方便，逻辑回归方法在建立土体液化概率预测模型中获得了广泛的应用。砂土液化判别的结果可看作是一个二分类问题，只有液化和不液化两种情况。在统计学中，广义线性模型被广泛应用于二分类问题的预测，逻辑回归(Logistic)模型就属于广义线性模型中的一种，除逻辑回归模型外，还有大量其他广义线性模型[27]。已有研究表明，最优液化模型与案例库有关，逻辑回归模型未必是土体液化判别的最优模型[28-29]。

笔者基于中国标贯试验的液化案例库，利用广义线性模型建立适用于土体液化概率判别的最优经验模型。首先介绍液化案例库和建立液化概率判别模型的方法；然后对建立的4种广义线性模型进行对比分析，给出最优模型；接着分析本文模型在不同烈度区、不同概率水平和不同埋深条件下的回判成功率；最后给出本文模型在预判分析中的应用实例。

1 液化案例库

文献[30]给出了中国基于标贯试验的159个震后调查案例，包含98个液化案例和61个非液化案例。该案例库是建立中国现行建规法的基础数据。表1给出了上述159个震后调查案例的来源。每个案例包含面波震级Ms、烈度I、标贯击数N、埋深ds和地下水位dw等5个常规参数。表2给出了案例库中这些参数的分布范围。

表1 液化案例库的基本信息

表2 液化案例库中参数的分布范围

图1为案例库中案例数随烈度的频数分布图。由图1可知，案例库包含的场地烈度范围为Ⅵ～Ⅹ度，在各个烈度区内，液化案例数均大于非液化案例数，且绝大部分案例处于Ⅶ、Ⅷ、Ⅸ烈度区。图2为案例库中案例数随埋深的频数分布图。由图2可知，案例库中仅有15个案例的埋深大于10 m，绝大部分案例的埋深处于0～15 m范围内；液化案例的埋深均处于0～11 m范围内，相对于非液化案例分布得更集中。

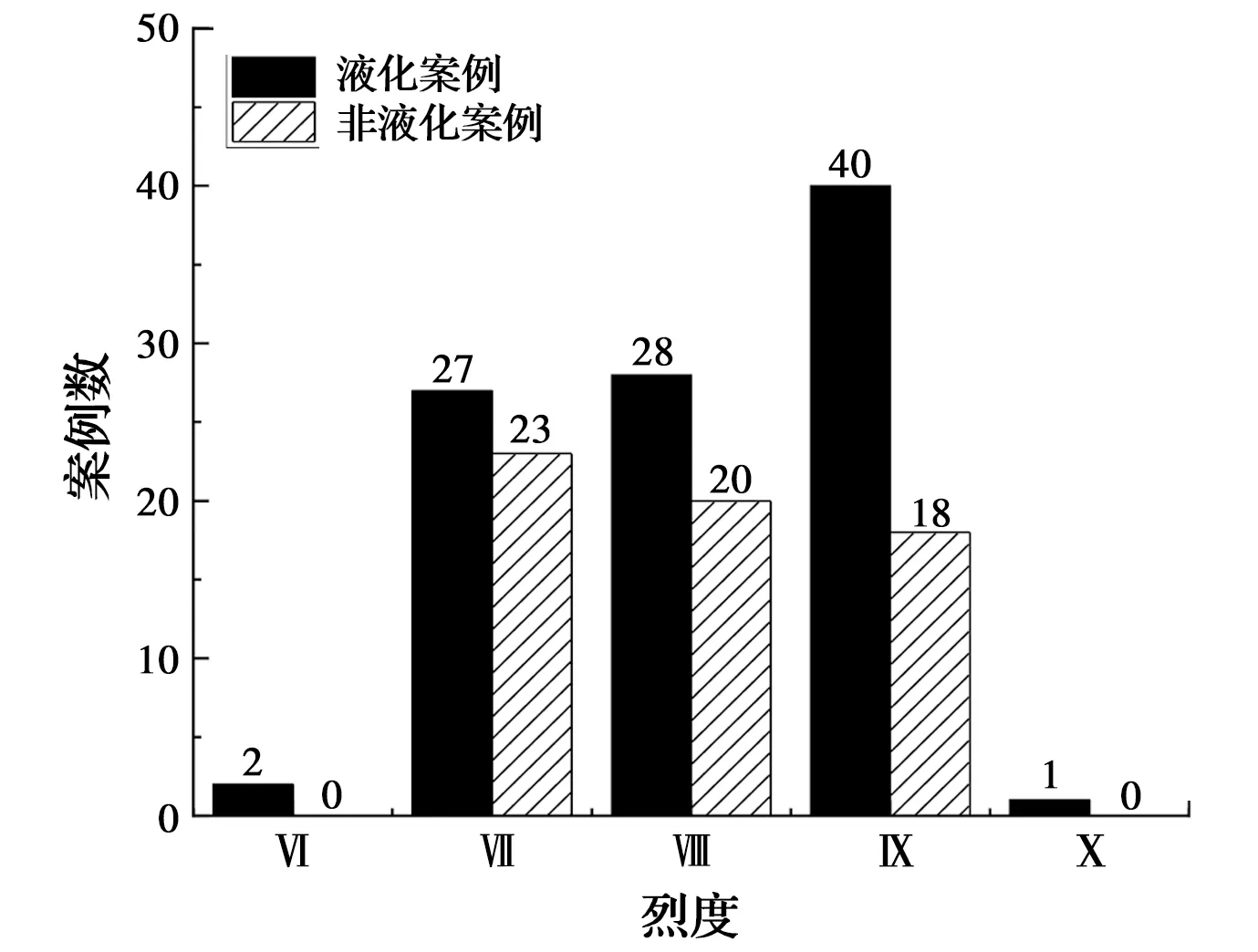
图1 案例随烈度的频数分布图Fig.1 The frequency distribution diagram of

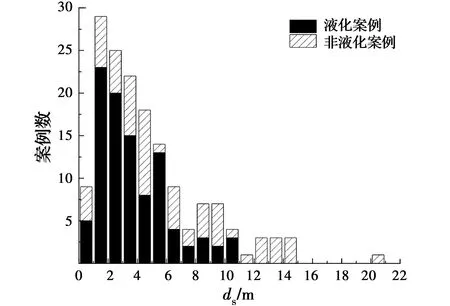
图2 案例随埋深的频数分布图Fig.2 The frequency distribution diagram of

由于不同国家和地区进行标贯试验的仪器设备和操作方法有所差别，若要将其他地区的液化调查资料用于分析中国液化判别准则，需考虑不同地区标贯试验结果的相关性，将不同来源的试验结果进行转换[30-31]。但由于相关转换关系的缺失，笔者未引入中国以外的场地液化案例。

2 建立液化概率判别模型的方法

2.1 广义线性模型

令X=[x1,x2…xn]，表示土体液化势判别中的自变量。令PL代表液化概率，令f(PL)表示液化概率PL的函数。假定f(PL)与自变量X之间存在式(1)所示关系[12]。

f(PL)=θ0+θ1x1+θ2x2+…+θnxn

(1)

式中：θ=[θ1,θ2…θn]为待标定的模型参数。液化概率PL的取值在0～1之间，式(1)等号右端的取值范围为-∞～+∞。为使式(1)左侧取值也位于-∞～+∞之间，f(PL)可取不同的函数形式，表3给出了f(PL)常用的4种函数形式[28]，式中Φ为标准正态分布的累积分布函数。按照上述规则建立的数学模型常被称为广义线性模型，可用于二元事件的概率预测。

在土体液化势分析中，标准贯入击数N可用来衡量土体抵抗液化的能力，循环应力比CSR可用来衡量地震荷载。令CSR7.5代表规准化为矩震级Mw=7.5的修正循环应力比。受已有文献的启发，笔者采用N和ln(CSR7.5)作为自变量。CSR7.5的计算公式为[6]

(2)

式中：amax为水平向地表峰值加速度，g；σv为测试点处的总上覆应力，可按式(3)估算。

σv=γsds

(3)

表3 广义线性模型

式中：γs为砂土重度。Seed等[32]和Idriss等[33]的案例库中案例的平均土体重度约为18.3 kN/m3[33]。文献[17]在采用文献[30]中的案例库进行液化分析时，假定案例的土体重度为19 kN/m3。本文采用的液化案例库也取自文献[30],为与上述研究保持一致，γs也取为19 kN/m3。σ′v为测试点处的上覆有效应力，可按式(4)估算。

σ′v=γsds-γw(ds-dw)

(4)

式中：γw为水重度；rd为剪应力折减系数，在工程实践中可按式(5)估算[34]。

(5)

由于案例库中案例的埋深大部分处于9.15 m内，为了简化计算，rd按式(6)估算。

rd=1-0.008ds

(6)

MSF为震级修正系数，按式(7)计算[6]。

(7)

式中：Mw为矩震级。试验表明，砂土抗液化能力与地震动持续时间(即振动次数)有关。地震动持续时间与震级密切相关。一般而言，震级越大，地震动持续时间越长，液化越容易发生[30]。因此，式(7)可基于地震震级来考虑地震持续时间对土体液化能力的影响。需要指出，表1给出的震级均为面波震级Ms，并非式(7)中的矩震级Mw。Youd等[6]指出，当Ms处于6～8范围内时，可取Ms≈Mw，故取Mw≈Ms。

将式(3)、式(4)、式(6)、式(7)带入式(2)，CSR7.5可按式(8)计算。

(8)

采用式(8)计算CSR7.5需要地表水平峰值加速度amax。由于中国液化案例库中只有烈度数据，缺乏amax记录，因此，需要根据烈度信息来推断水平峰值加速度amax。根据以往经验，液化案例库中Ⅶ、Ⅷ、Ⅸ度区的amax分别取为0.1g、0.2g和0.4g[35-36]。参照《中国地震烈度表》(GB/T 17742—2008)[37]，Ⅵ和Ⅹ度区对应的amax分别取0.05g和0.8g。由图1可知，表1中液化案例主要位于Ⅶ、Ⅷ、Ⅸ度区，而位于Ⅵ和Ⅹ度区的案例数分别为2和1。

2.2 模型标定方法

令D代表用于模型标定的案例库，令nL、nNL分别代表案例库中的液化案例数和非液化案例数。实际上，由于震后调查中通常更重视收集液化案例，导致案例库中液化案例的比例可能高于真实世界[38]。为考虑上述抽样偏差的影响，可采用加权极大似然法对模型参数进行标定。令QS和QP分别代表案例库和真实世界中液化案例的比例。考虑抽样偏差后，案例库的加权似然函数对数可按式(9)计算[7]。

(9)

式中：PLi为第i个案例的液化概率值；wL和wNL分别为液化案例和非液化案例的权重因子，可按式(10)计算。

(10a)

(10b)

式中：QP可取为0.456[28]。将表3中的广义线性模型带入式(9)，即可获得相应模型的似然性函数。根据最大似然性原理，将其似然性函数进行最大化，即可获得模型的最优参数θ*。

2.3 模型比较方法

对于同一个案例库，利用不同的广义线性模型可以建立不同的液化概率预测模型。由于不同模型对数据的拟合效果不同，不同模型为最优模型的概率也有所不同。贝叶斯信息准则(Bayesian Information Criterion, BIC)能同时考虑模型对案例库的拟合效果和模型复杂程度，常用于对不同模型的优劣进行排序。令Mi代表第i个模型，其贝叶斯信息准则的表达式为[39]

BICi=-2ln[L(θ*|Mi,D)]+kiln(n)

(11)

式中：L(θ*|Mi,D)为Mi的似然函数极大值；ki为Mi中参数的个数；n为案例库中的案例数。在给定数据库D的情况下，模型Mi的模型概率可以由式(12)计算[38]。

(12)

式中：r为模型总数；Δi(BIC)可由式(13)计算[38]。

(13)

根据式(12)计算出不同模型的模型概率后，即可通过模型概率对模型进行比较。模型概率越高，表明模型受数据支持的程度越高。

3 模型标定和比较

表4给出了根据式(9)和极大似然法获得的不同广义线性模型的模型标定结果。图3给出了4种模型在6种液化概率(1%、10%、30%、50%、70%和90%)下的液化概率等势线。图3中，横坐标为标贯击数N，纵坐标为修正循环应力比CSR7.5，实心圆点代表液化案例，空心圆点代表非液化案例。在给定概率水准的条件下，等势线上方的案例点判别为液化，下方的案例点判别为不液化。从图3可以看出：

1)随着液化概率的增大，4种模型的等势线有向左上方移动的趋势，表明越来越多的液化点判别为不液化，判别结果也越来越保守。

2)当液化概率较小(PL= 1%)时，4种广义线性模型之间的差异较大；其中，C-log-log模型获得的等势线位于最右侧，表明对于相同的CSR7.5值，C-log-log模型需要更大的N值才能满足与其他模型相同的液化概率，因而其液化判别结果最为保守。

3)当液化概率为10%时，Logistic、Probit、Log-log模型的预测结果类似，而C-Log-log模型获得的等势线位于最右侧，表明C-log-log模型较其他模型更为保守。

4)当液化概率在30%～70%之间时，4种模型的临界线位置比较接近，液化判别结果相差不大。

5)当液化概率为90%时，Logistic、Probit以及C-Log-log模型预测结果类似，而Log-log模型获得的等势线位于最左侧，表明其预测结果最不保守。

表4 模型标定及比较

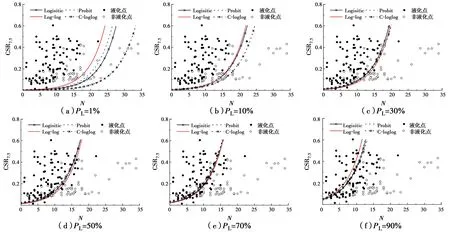
图3 不同液化概率水平下模型的比较Fig.3 Comparison of models under different liquefaction

由上述分析可知，不同模型在不同液化概率下的临界线位置不同，液化判别结果也有所不同。由于很难通过岩土力学知识对不同模型的优劣进行直接比较，本文采用统计学中“模型概率”这一指标对不同模型与数据的符合程度进行排序。表4给出了4种模型的最优模型概率。从表4可以看出，Log-log模型的最优模型概率最高，为35%，说明Log-log模型与案例库的符合程度最高，为4个模型中的最优模型。相比而言，文献中常用的Logisitc模型也有较高的模型概率，说明该模型也有一定的合理性。

为便于使用，将式(8)代入表4中的Log-log模型，可得土体液化概率计算公式

(14)

由式(14)可知，在给定地震动参数(amax,Mw)和土层信息(ds,dw)的条件下，土体液化概率PL由该处土体对应的标贯锤击数N唯一确定。该锤击数可视为液化概率水平为PL条件下的临界锤击数Ncr。当实测锤击数大于Ncr时，土体的液化概率小于PL；当实测锤击数小于Ncr时，土体液化概率大于PL。基于式(14)，给定液化概率PL下的临界标贯击数Ncr可按式(15)计算。

1.41ln(1-0.008ds)+3.61ln(Mw)+ln[-ln(PL)]}

(15)

由于液化案例库中土类大部分为细砂、粉砂和粉细砂[30,40]，因此式(15)适用于饱和砂土和饱和粉土的液化判别。需要指出，在2008年四川省汶川地震中发现了砂砾土液化的现象[41]，式(15)不适用于砂砾土的液化判别。以中国西南板块活跃地区为例，式(15)可用于该区域内饱和砂土和饱和粉土的液化判别，但对该区域内的砂砾土场地不适用。

4 回判分析

4.1 与建规法的对比

建规法中标贯击数临界值的计算公式为

(16)

式中：ρc为黏粒含量百分率，当小于3或为砂土时，应取3[3]。利用建规法进行回判分析时需要案例的ρc值。液化案例库取自文献[30]，案例缺少黏粒含量信息。文献[30]案例库中案例的土类大部分为细砂、粉砂和粉细砂等砂土[30,40]。文献[40,42]在对文献[30]案例库进行液化判别时，所有案例的ρc值均取3。为与上述研究保持一致，本文利用建规法进行回判分析时ρc也取为3。N0为标贯击数基准值。利用建规法进行回判分析时需要案例的N0值，可根据案例的实际烈度对应的峰值加速度获得相应的标贯击数基准值；β为调整系数，可根据实际震级M按式(17)计算。

β=0.25M-0.89

(17)

利用式(16)和式(17)计算得到的标贯击数临界值Ncr对应的液化概率水平为32%；用于建立式(16)的数据来源与本文案例库基本相同[43]。为便于与建规法进行比较，本文将PL=32%带入式(15)，由此获得的临界标贯击数与式(16)中标贯击数临界值进行比较。表5给出了式(16)和本文方法计算获得的锤击数临界值在不同烈度下的回判成功率。由表5可知，式(16)和本文方法对液化案例的总体回判成功率均高于非液化案例，这与这两种判别方法对应的液化概率为32%，偏于保守有关。表5还表明，在Ⅶ度区内，本文方法对液化案例的回判成功率高于式(16)，对非液化案例的回判成功率略低于式(16)；在Ⅷ和Ⅸ度区内，本文方法对液化案例的回判成功率高于式(16)，对非液化案例的回判成功率与式(16)相当；从全部案例的回判成功率来看，本文方法的回判成功率在不同烈度区内均高于式(16)。

表5 32%概率下的Log-log模型与建规法公式在不同烈度下的回判成功率

4.2 不同液化概率水平下的回判成功率

图4给出了式(15)在不同液化概率下的回判成功率。从图4中可以看出，当PL= 10%时，式(15)对液化案例的判别成功率接近100%，而对非液化案例的判别成功率约为50%，判别结果显著偏于保守。随着液化概率的增大，式(15)对液化案例的回判成功率越来越低，对非液化案例的回判成功率越来越高，而总体回判成功率则整体呈先略增大后减小的趋势，在液化概率为30%和50%时取得最大值。因此，随着液化概率的增大，液化案例被判别为不液化的比例持续增加，式(15)越来越偏于不保守；与此同时，式(15)计算得到的临界标贯击数减小，表明土体抵抗地震荷载所需的标贯击数降低，故在工程实践中将更为经济。为达到安全性与经济性的平衡，采用的设计安全系数值对应的液化概率水平一般为15%～35%[9,15]。

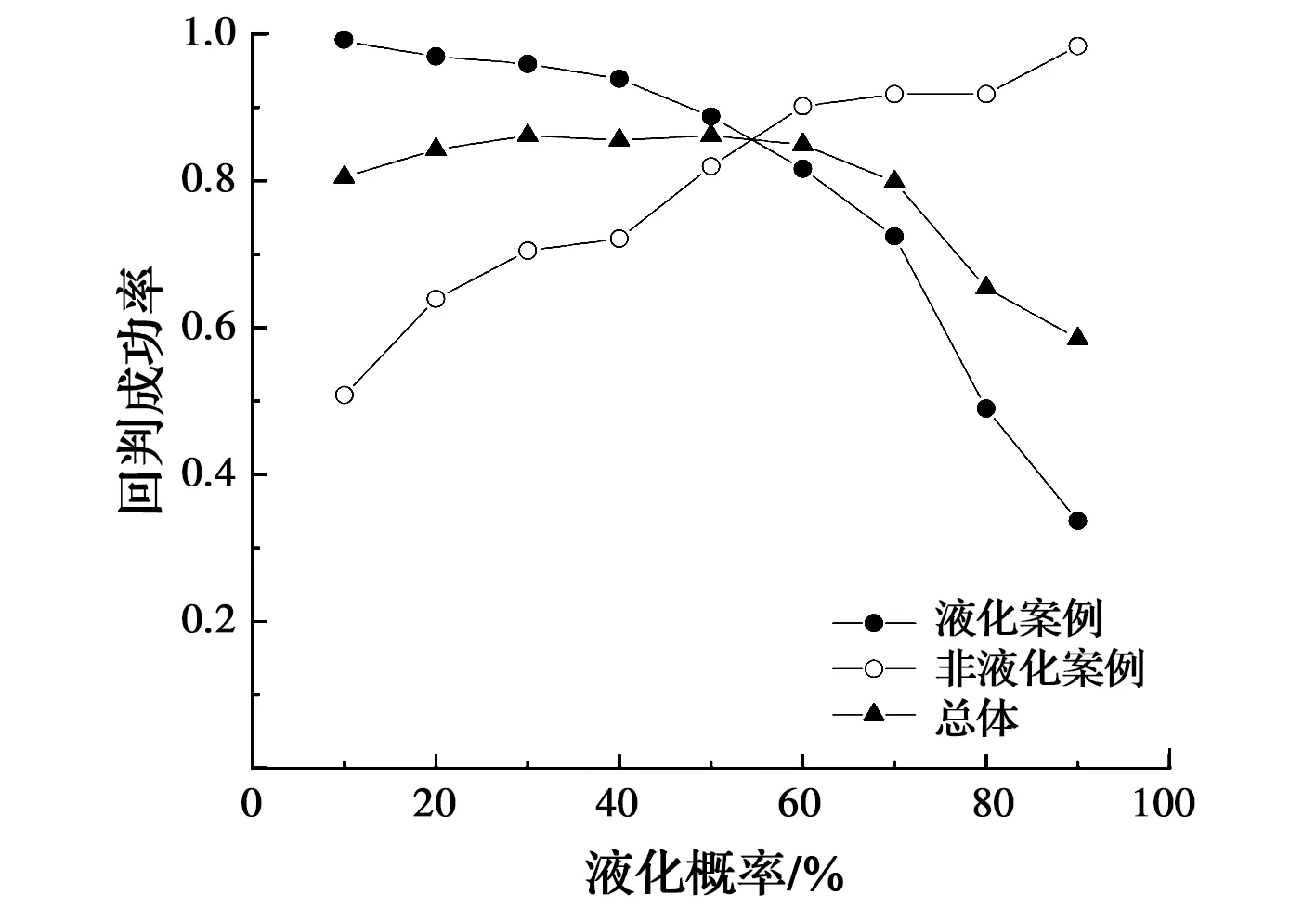
图4 Log-log模型在不同液化概率水平下的回判成功率Fig.4 The verification success ratio of Log-log model under different liquefaction

4.3 不同埋深的回判成功率

案例库159个案例中埋深大于11 m的案例仅有11例，且均为非液化案例；埋深大于15 m的案例仅有1例。为了简化计算，式(8)中rd近似取ds≤9.15 m时的表达式代入。表6给出了32%液化概率下式(15)在不同埋深条件下的回判成功率。从表6可以看出，32%液化概率下的式(15)对于埋深小于9.15 m和埋深大于9.15 m案例的总回判成功率均在80%以上，在一定程度上说明了式(15)的可靠性。不过，由于本文案例库的局限性，式(15)在埋深大于15 m时的判别精度还需进一步研究，在未来的震后场地调查中尤其需注重深埋条件下案例的收集和分析。

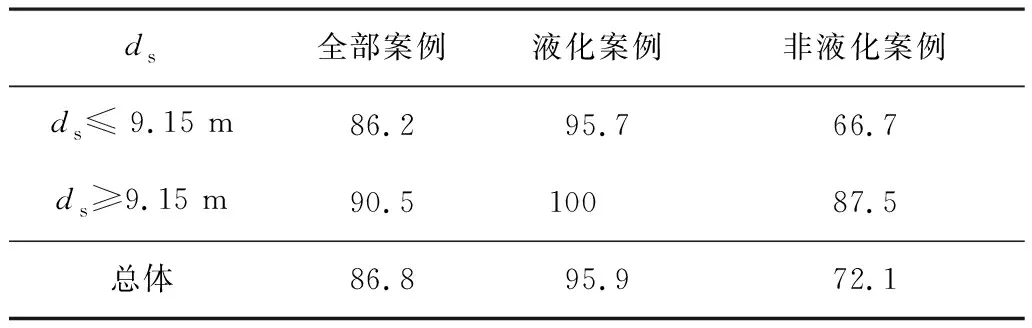
表6 32%概率下的Log-log模型在不同埋深下的回判成功率

5 液化判别及实例分析

应用式(15)进行液化判别时，需要的地震动参数包括设计地震在本场地的地表峰值加速度amax及地震震级Mw。中国抗震设计规范提供了不同地区的设计基本地震加速度值及设计地震分组，但没有提供设计地震的震级。不过，建规法给出了不同设计地震分组条件下的调整系数值。如式(17)所示，各设计地震分组对应的调整系数β值主要由震级M确定。表7给出了建规法中不同设计分组对应的调整系数，将这些调整系数带入式(17)，即可获得不同设计地震分组对应的震级。

表7 设计地震分组与矩震级的对应关系

5.1 实例一

图5给出了1975年海城地震中盘锦化肥厂场地的标贯试验数据[33,44]。该场地在海城地震中观察到了土体液化现象。场地地下水位为1.5 m，地表以下2.6 m为黏土；2.6～20.0 m为粉土和细砂。

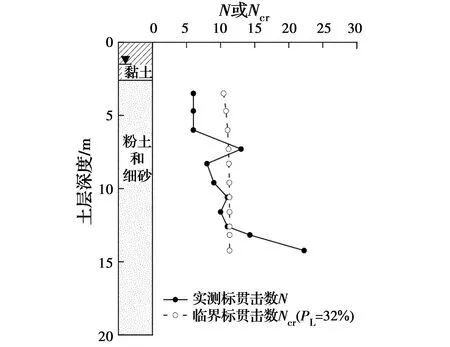
图5 海城地震中盘锦化肥厂场地的N和Ncr随土层深度的变化Fig.5 Variation of N and Ncr with soil depth at the Panjin Chemical Fertilizer Plant site during the 1975

根据现行建规法中附录A可查得盘锦市的设计基本地震加速度值amax=0.10g，设计地震分组属于第2组。由表7可知，设计地震分组第2组对应的矩震级Mw= 7.36。为与建规法对应的概率水准一致，本算例取PL= 32%。将amax、ds、dw、Mw和PL等5个参数代入式(15)，即可求得各测试点的标贯击数临界值Ncr。为方便比较，表8和图5中分别给出了各点处土体的标贯击数临界值。在图5中，当标贯击数临界值位于实测值右侧时，表明土体受到的地震荷载大于土体的抗液化强度，即土体会发生液化。由图5可知，地表以下3～13 m范围内土层发生液化的可能性较大。

表8 海城地震中盘锦化肥厂场地的液化判别结果

该方法还可直接用于计算土体的液化概率。事实上，取amax= 0.10g、Mw= 7.36，将各点测得的ds、dw和N代入式(14)，即可求得各测试点的液化概率值PL。表8中也给出了各点的液化概率计算结果。由表8可知，地表以下3～13 m范围内土体液化概率较大，与图5中观测结果一致。

5.2 实例二

唐山地震中，在位于河北省乐亭县的某场地[44]观察到了液化现象，图6给出了该场地的土层信息和标贯试验结果。场地地下水位为1.6 m，地表以下1.8 m为黏土，1.8～15.0 m为细砂。

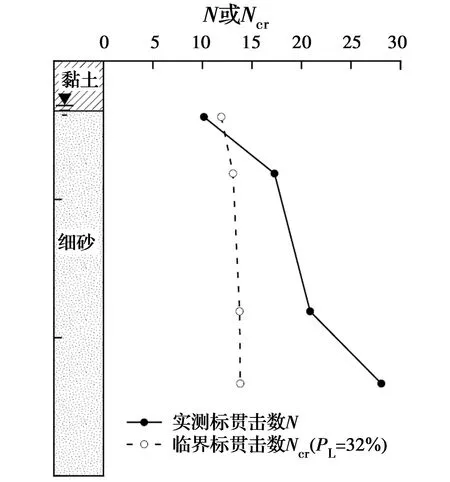
图6 唐山地震中乐亭县某场地的N和Ncr随土层深度的变化Fig.6 Variation of N and Ncr with soil depth at a site in Leting during the 1976 Tangshan

根据现行建规法中附录A可查得乐亭县的设计基本地震加速度值amax=0.15g，设计地震分组属于第3组。由表7可知，设计地震分组第3组对应的矩震级Mw=7.76。将amax、ds、dw、Mw和PL(PL=32%)等5个参数代入式(15)。图6给出了各测试点的标贯击数临界值Ncr，由图6可知，该场地地表以下2～3 m范围内土体发生液化的可能性较大。

6 结论

利用广义线性模型，基于中国液化案例库建立了4种液化概率判别模型，并对模型进行了比较，获得以下主要结论：

1)当液化概率小于10%时，4种模型之间的差异明显，其中C-log-log模型的预测结果最为保守；当液化概率在30%～70%之间时，4种模型预测结果类似。当液化概率等于90%时，Log-log模型的预测结果最不保守。

2)贝叶斯模型比较表明，Log-log模型为最优模型的概率最高，说明Log-log模型与案例库中数据的符合程度最高，为最优模型。基于Log-log模型，提出了适用于中国的液化概率计算公式，并给出了指定液化概率条件下标贯击数临界值的计算公式。

3)回判分析表明，提出的Log-log模型在不同烈度区内的回判成功率高于现行建筑抗震设计规范。