基于矢量地震动强度参数的隧道结构易损性分析

张建辉，黄忠凯，刘祥勇，朱先发，张冬梅

(1.南通城市轨道交通有限公司，江苏 南通 226007；2. 同济大学 岩土及地下工程教育部重点实验室；地下建筑与工程系，上海 200092)

隧道是城市生命线工程和社会公共基础设施的重要组成部分，更是现代大都市的交通命脉，其地震安全及风险分析已成为城市防灾减灾研究的重要课题。相比地表建筑结构，人们往往认为隧道结构相对安全，但近数十年来已发生数起地震引发的隧道结构严重破坏甚至坍塌的案例[1-4]。比如，在2008年中国汶川8.0级地震中，大量隧道发生严重受损状况，多处发生混凝土剥落及掉块、钢筋出露、衬砌渗水、衬砌失效及坍塌等现象[5]，其中，仅四川灾区发生各种程度破坏的隧道就有56座，造成了巨大的经济损失。因此，隧道结构地震易损性分析研究对降低经济损失，顺利开展抢险救援工作具有极其重要的意义。

地震易损性分析能从概率的角度定量表达结构的抗震性能，其定义为，在不同地震动强度(Intensity Measure,IM)下，结构性能达到或超越不同破坏极限状态的条件概率。由定义可知，地震动强度参数IM是结构地震易损性分析的一个关键因素，该因素与结构的地震响应密切相关。因此，地震动强度参数IM的选择对于隧道地震易损性分析尤为重要。易损性分析中常用的IM主要有两种，一种是标量IM，即采用单个IM进行地震易损性分析；另一种是矢量IMs，即采用两个及以上的IMs进行地震易损性分析，目前前者使用较多而后者使用较少。崔臻等[6]、Argyroudis等[7-8]、张轶群[9]、钟紫蓝等[10]及Huang等[11]都采用标量IM(如PGA及PGV等)对不同隧道结构展开了地震易损性分析，获得的地震易损性曲线可用于相应隧道地震风险分析中。但上述研究大多采用标量IM展开[6-11]，且往往依据经验选用IM，并未对IM的合理性选择进行探讨。另一方面，由于地震动的复杂性，采用单一的标量IM不能表达其他地震动强度信息，从而导致预测的隧道抗震性能与实际存在较大离散性[10]。与标量IM相比，矢量IMs可以更准确地反映地震动的不确定性，因此，其预测的隧道抗震性能与实际相关性更好。建筑和桥梁相关研究[12-14]表明，相较于使用矢量IMs，基于标量IM的易损性分析不能精确获得结构破坏概率，从而引起结构抗震性能误判。然而，目前基于矢量IMs的隧道地震易损性分析较少，亟待进一步展开相关探索。

鉴于此，笔者以软土浅埋隧道为研究对象，分别展开基于标量和矢量地震动强度参数的地震易损性分析。选择15个常见的地震动强度参数IMs，根据有效性、实用性和效益性等评价指标，对隧道地震易损性分析的合理地震动强度参数进行研究，并利用最优地震动强度参数建立了基于标量IM的隧道地震易损性曲线；采用获得的两个合理地震动强度参数，建立了基于矢量IMs的隧道地震易损性曲面，并与上述地震易损性曲线进行了对比。

1 隧道地震易损性分析方法

1.1 破坏指标DI定义

根据美国生命线联盟(American lifelines alliance，ALA)[15]的建议，地震造成的隧道破坏状态一般可以划分为5种，即无破坏、轻微破坏、严重破坏及完全破坏。隧道领域中使用最多的破坏指标DI定义为衬砌的实际弯矩(MSd)与容许弯矩(MRd)之比[7]，如式(1)所示。

DI=MSd/MRd

(1)

式中：隧道衬砌截面实际弯矩MSd通过静力和地震荷载下的动力分析计算得到；容许弯矩MRd则根据截面属性及截面地震轴力N，通过极限承载力分析计算得到。基于已有研究成果[7-8]，表1给出了隧道破坏状态定义。

表1 隧道破坏状态定义[7]

1.2 基于标量IM和矢量IMs的地震易损性分析

地震易损性是指结构在不同地震动强度下超越不同破坏状态的条件概率，一般可用式(2)表示。

P[ds>dsi|IM]=Φ(λ/βtot)

(2)

式中：P[·]是某一地震强度下结构超过不同破坏状态的概率；Φ是标准正态分布累计密度函数；ds为破坏状态；IM为选用的地震动强度参数；λ和βtot为均值和方差。

当采用标量IM时，λ可用式(3)表示。

λ=a+blnIM

(3)

式中：a和b为各个计算工况对应的IM和破坏指标DI的对数线性回归系数。

当采用矢量IMs时，即选用两个地震动强度参数IM1及IM2，λ可用式(4)表示。

λ=x+ylnIM1+wlnIM2

(4)

式中：x、y和w为各个计算工况对应的IM1及IM2和获得的破坏指标DI的对数线性回归系数。

参数βtot表达了易损性曲线的不确定性大小，可以用式(5)表示。

(5)

式中：βds为破坏状态ds定义的不确定性；βC为隧道结构响应和抗力的不确定性，参数βds和βC分别取值为0.4和0.3[7-8]，而βD/IM为输入地震动不确定性，与地震需求相关，由输入不同地震波计算得到的破坏指标与拟合回归曲线的标准偏差确定，如式(6)所示。

βD/IM=[Sr/(n-k)]0.5

(6)

式中：Sr为回归分析中离散点与回归直线的残差平方和；n为数据点个数，即总计算工况数；当采用标量IM时，k=2，而当采用矢量IMs时，k=3。

2 土-隧道系统数值分析模型

2.1 隧道及土层参数

以上海软土地区典型浅埋盾构隧道为例，隧道拱顶埋深h为9 m，隧道直径d为6.2 m，衬砌厚度t为0.35 m。选取上海城区IV类场地中3个典型土体断面，分别用IV-1、IV-2和IV-3标记，断面高度为100 m。其中，地下0～75 m为黏土，其泊松比n为0.30，而75 m以下为砂土层，其泊松比n为0.33，地下100 m以下为弹性基岩，其剪切波速取为500 m/s。黏土和砂土G-γ-D曲线分别如图1所示，其中G为土体剪切模量，Gmax为土体最大剪切模量，γ为土体剪切影响，D为土体阻尼比。图2给出了3个土体断面关键参数，如密度ρ、黏聚力c、摩擦角φ及剪切波速Vs等沿深度的分布，计算可得其基本周期分别为1.59、1.41、1.23 s。

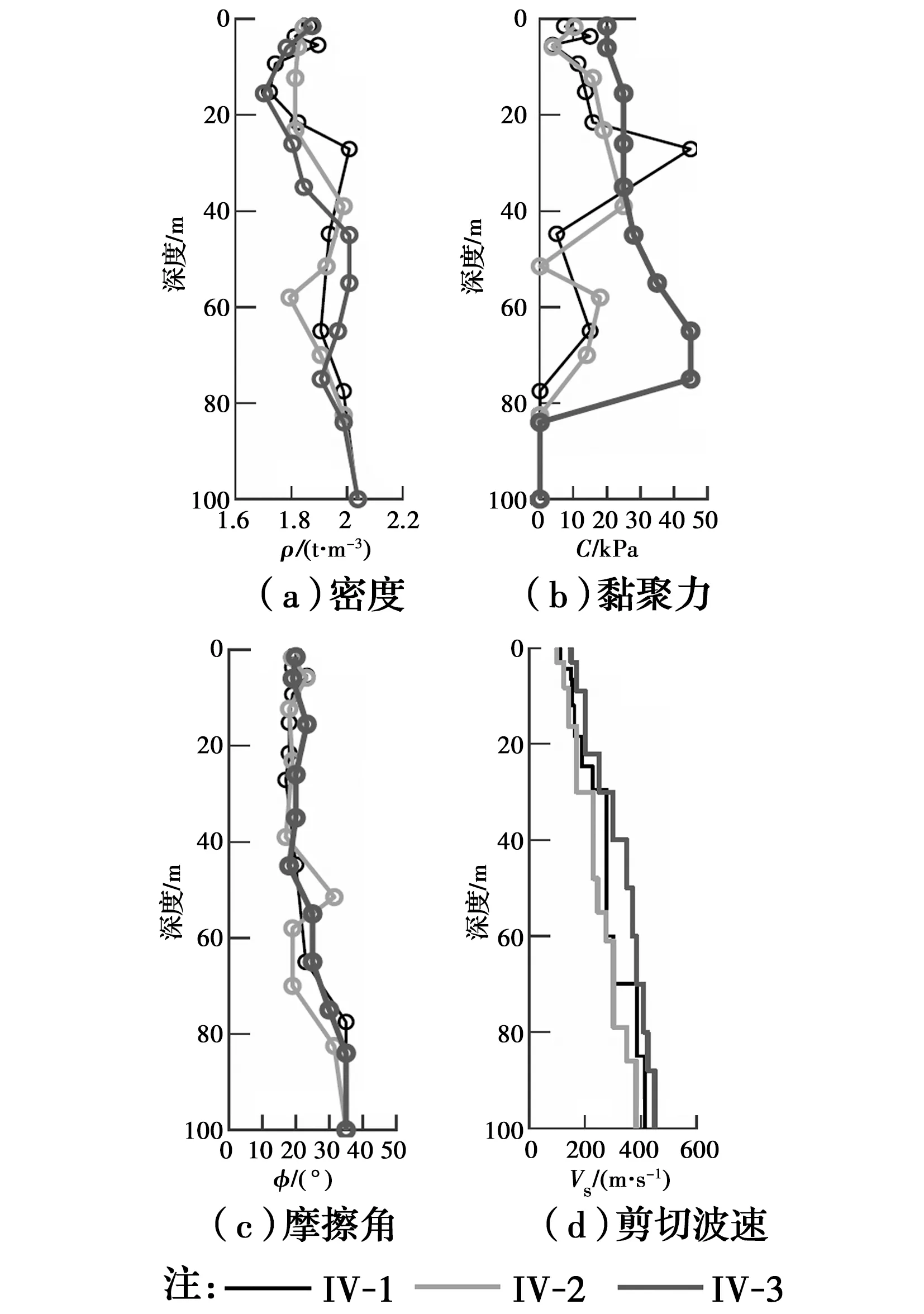
图2 土层关键力学参数Fig.2 Critical soil mechanical

2.2 地震记录选择

已有研究[10]表明，合理选择10～20条地震动记录作为模型输入，即能合理控制地震动输入的不确定性影响。依据研究场地的特征，从美国太平洋地震研究中心(PEER)网站遴选了12条地震记录，具体信息如表2所示，所选的地震波矩震级Mw在5.01～7.36级之间，断层距R在1.63～77.32 km之间。

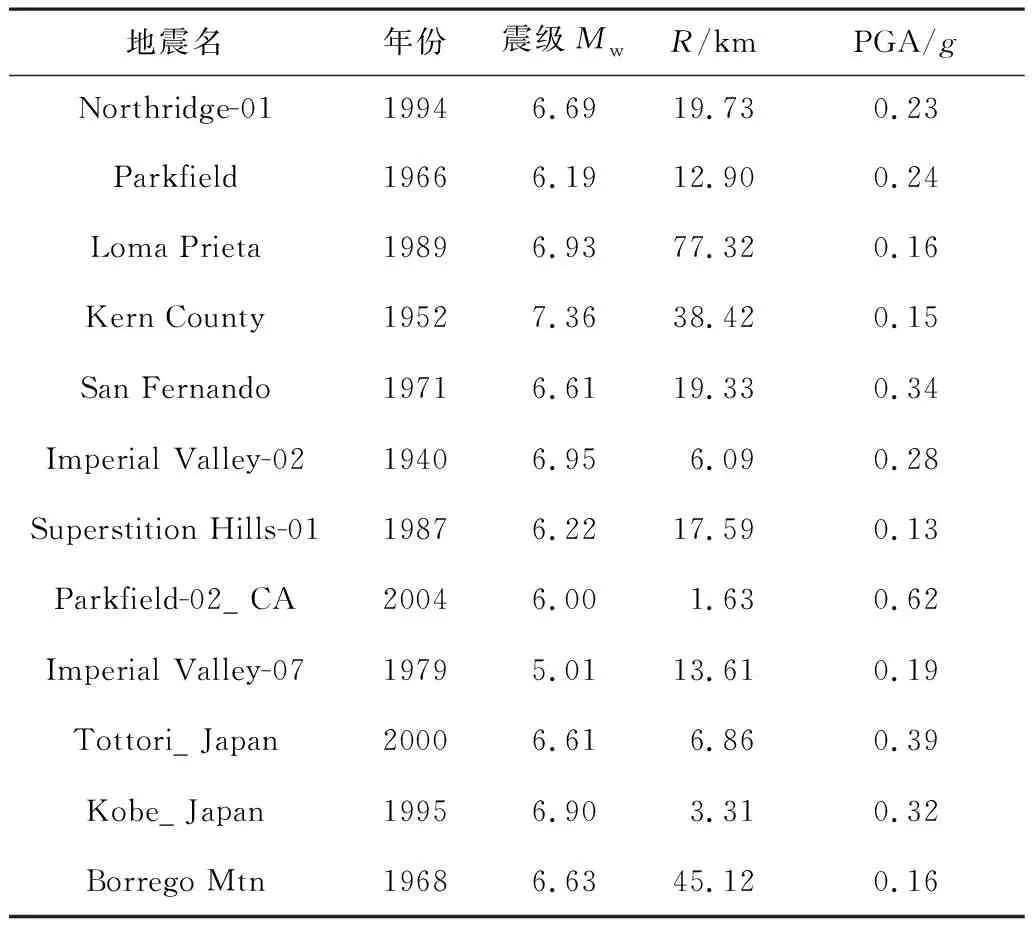
表2 选取的地震记录

图3给出了所选12条地震波的放大系数反应谱与中国规范谱[16]的对比，可见，所选12条地震波反应谱均值与规范反应谱较吻合。

图3 地震波放大系数谱Fig.3 Acceleration response spectra of the

2.3 计算模型

采用Abaqus软件按平面应变条件建立动力分析模型，典型工况计算模型如图4所示。为了消除模型边界效应对隧道结构地震反应的影响，模型有限元宽度选为400 m，远大于地铁抗震规范[17]建议的6倍结构宽度。在模型侧向边界设置捆绑约束，使两侧边界等高处节点可以在地震作用下做水平剪切运动，拥有相同的侧向变形。模型底部边界施加阻尼器，阻尼器参数C参考Lysmer等[18]的方法，可由基岩密度ρ、基岩剪切波速Vsb及单个阻尼器所占的网格面积A相乘得到，计算式为

C=ρ×Vsb×A

(7)

根据Lysmer等[18]推荐的方法对土体和隧道网格尺寸进行合理划分，并将隧道结构周围的土体网格进行加密处理，保证计算结果的准确性。对于土-隧道结构接触界面，其法向为硬接触，切向利用罚刚度算法模拟。分别采用四节点平面应变减缩积分单元(CPE4R)及两节点梁单元(B21)来模拟土体及衬砌。隧道衬砌利用弹性本构模拟，土体采用等效线性法结合摩尔库伦弹塑性模型模拟。土体阻尼比近似采用5%，由于动力响应分析中土体的阻尼比动态变化，因此，难以真实选取特定的阻尼比展开计算，许紫刚等[19]针对地下结构地震反应分析中场地瑞利阻尼构建方法展开了深入研究，提出了一种新的瑞利阻尼系数计算方法，但该方法较复杂。为了简化，按经验选取5%作为土体阻尼比，该简化方法和阻尼比数值也被其他学者[20-21]广泛采用。使用双频率法校正的瑞利阻尼形式，阻尼参数校正选择土体断面的基本频率f和其5倍频率5f。

根据上述参数建立了土体-隧道结构计算模型，如图4所示。为了合理模拟隧道结构的受力状态，首先进行地应力平衡，获得结构和土体在重力下的初始应力分布，然后在模型底部通过阻尼器水平方向施加竖向传播的剪切地震波(即选择的地震动记录)。为了获得隧道在不同地震强度下的动力响应，每条波的峰值加速度以0.1g为增量，从0.1g调幅到1.0g，继而展开大量非线性动力分析计算。值得注意的是，为了简化分析，并未考虑竖向地震动影响[22]，仅针对水平剪切地震动展开进一步分析。

3 地震易损性分析

3.1 基于标量IM的地震易损性曲线建立

1)地震动强度参数IMs

地震动强度参数是影响隧道地震易损性分析离散性和准确性的关键因素[7]，因此，有必要对其展开深入探讨。表3给出了分析所用的15个地震动强度参数IMs，其定义和计算公式可参阅表中相应的参考文献，根据它们的物理意义，一般可将这15个IMs归为3类：与振动幅值相关的振幅型IMs，如PGA、PGV、PGD、SMA和SMV；与频谱特性有关的频谱型IMs，如ASI、VSI和HI；与幅值及频谱特性有关的综合型IMs，如Arms、Vrms、Drms、IA、IC、CAV和SED。

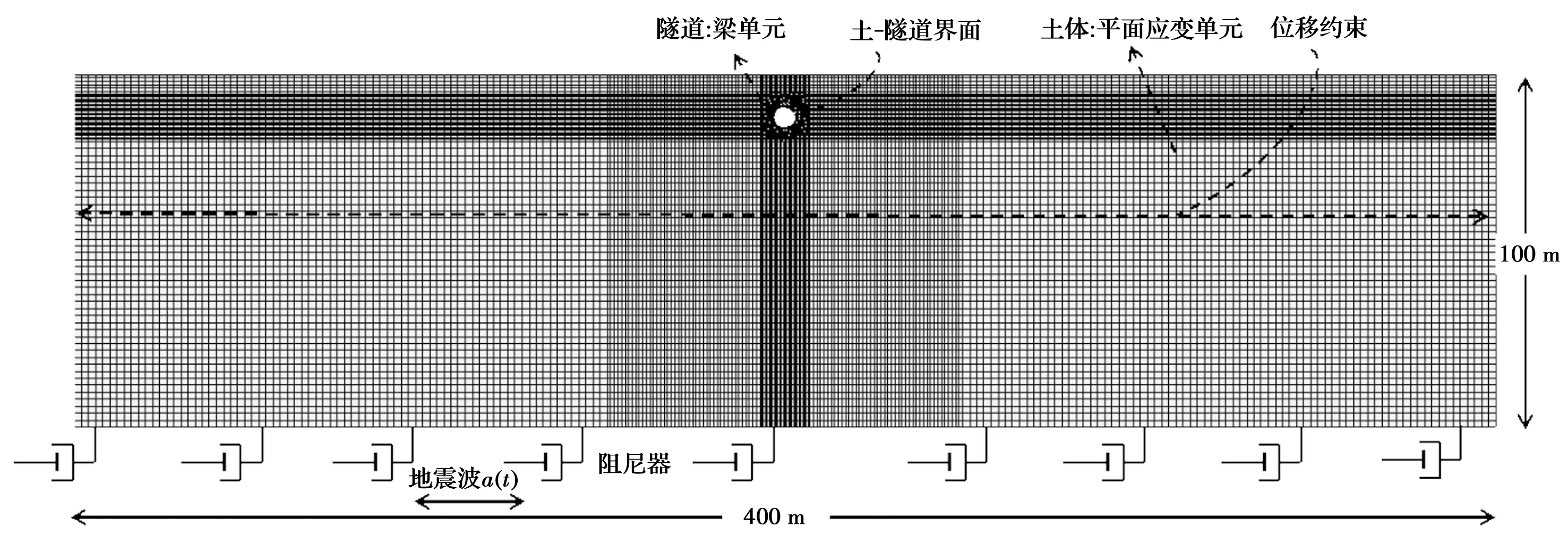
图4 计算模型

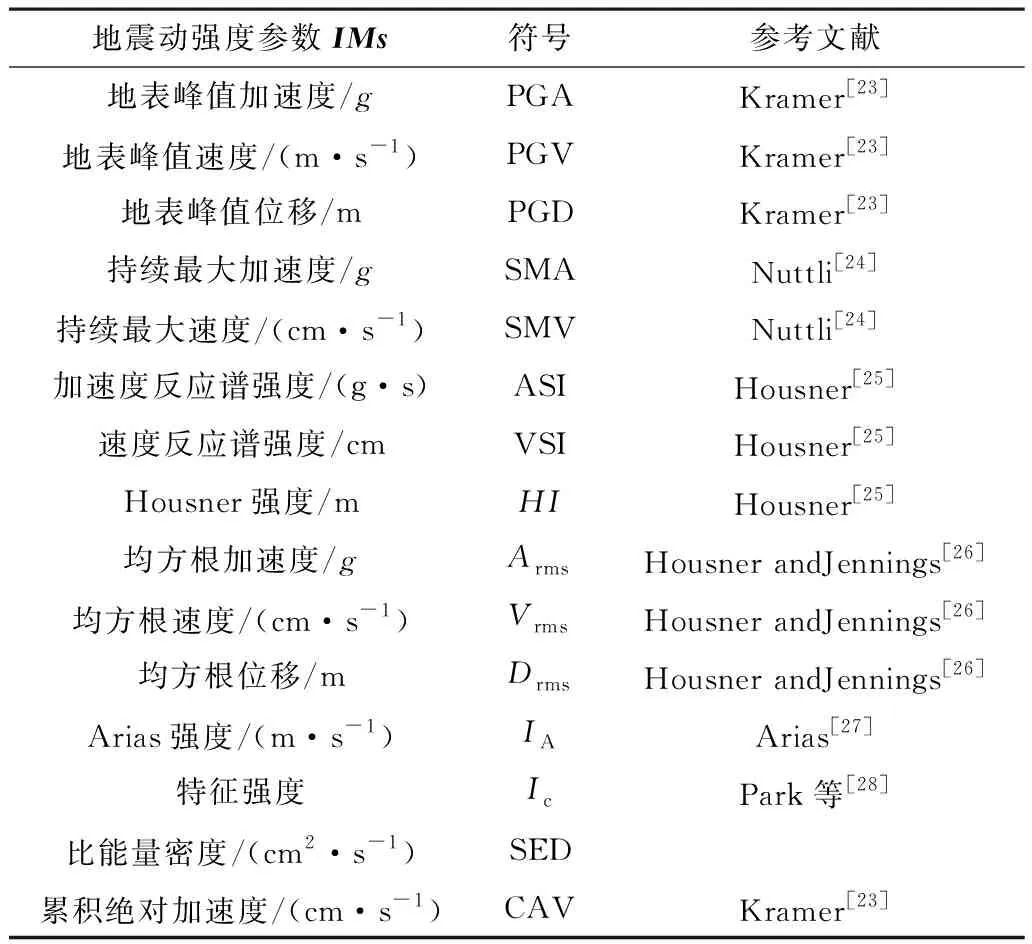
表3 选取的地震动强度参数IMs

2)破坏指标DI与标量IM回归分析

通过展开非线性动力分析，获得破坏指标DI和15个地震动强度参数IMs的大量样本。采用“云图法”[7]进行地震易损性分析，地震动强度参数IM与破坏指标DI的关系采用对数线性回归方式表达，如图5所示。

图5 基于云图法的易损性分析Fig.5 Cloud method-based vulnerability

开展相应的回归分析，其中，破坏指标DI与4个典型IMs(PGA、PGV、SMA和SMV)的对数回归关系如图6所示，其余IMs回归公式的相关系数如表4所示。

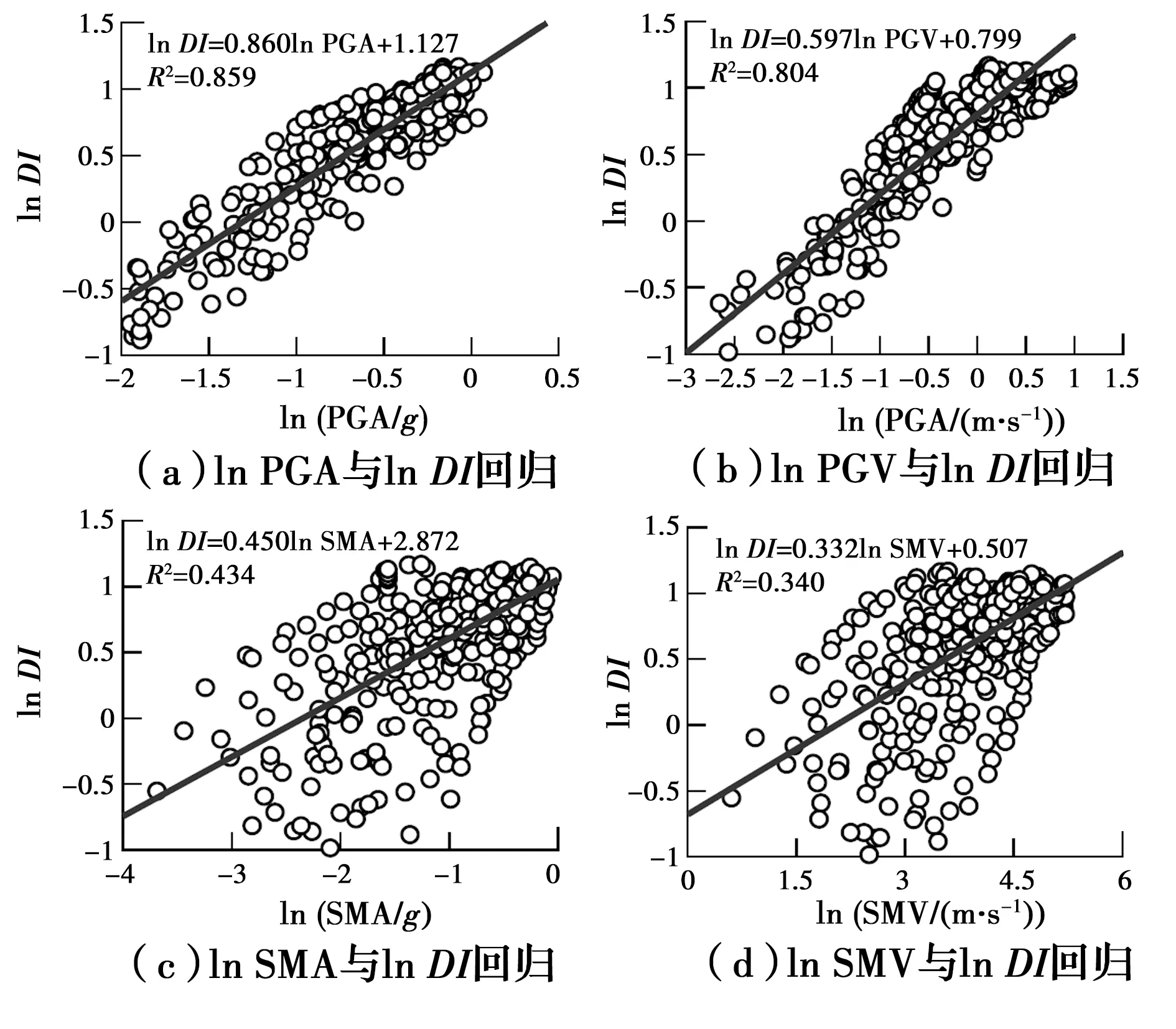
图6 破坏指标与4个典型地震动强度参数的回归分析Fig.6 Regression analyses between DI and four representative seismic

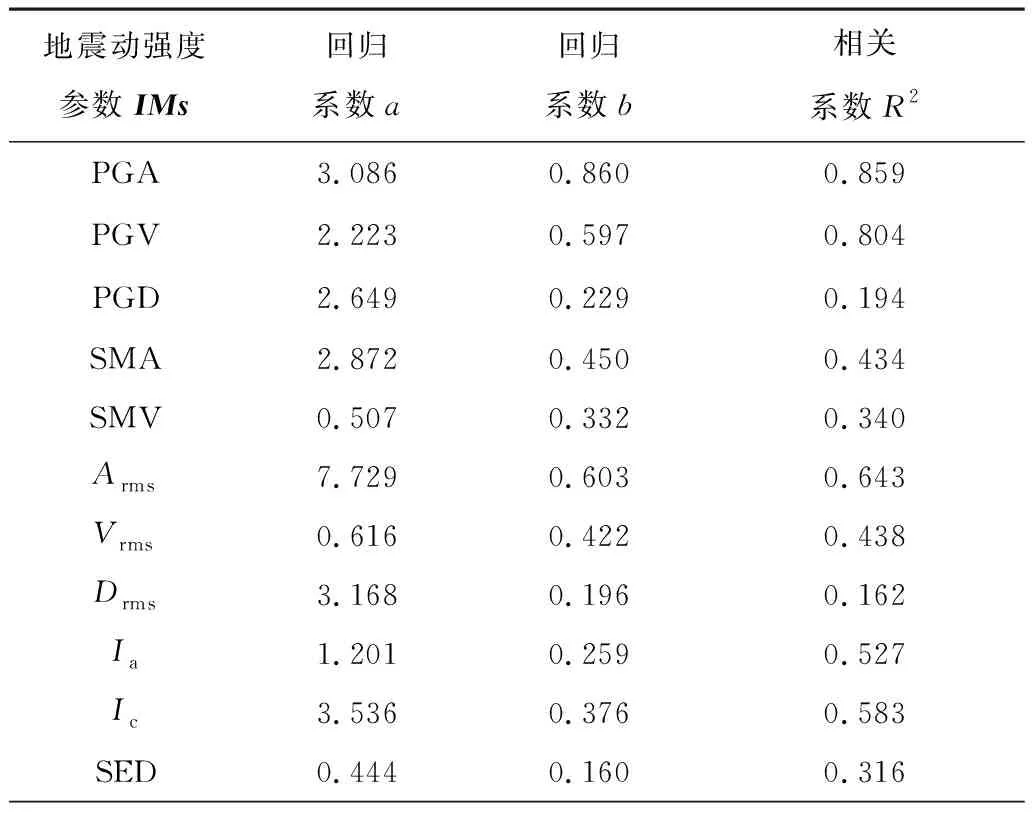
表4 回归参数

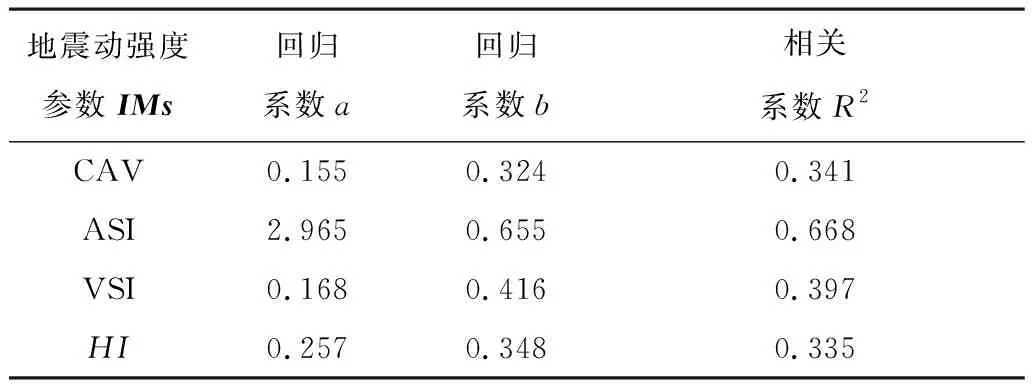
续表4

3)有效性分析

有效性体现了破坏指标DI预测值与实际值的离散程度，可采用式(4)中的标准差βD/IM来分析。标准差βD/IM越小，则该地震动强度参数IM的有效性越好；反之，标准差βD/IM越大，则有效性越差。图7给出了15个IMs对应的标准差βD/IM。由图7可知，PGA的有效性最好，其标准差βD/IM最小，为0.186，其次是PGV，标准差βD/IM为0.219；Drms的标准差βD/IM最大，为0.453，其次为PGD，标准差βD/IM为0.444。从不同IMs类型的角度来看，对于振幅型地震动强度参数，PGA的有效性最好，PGD的有效性最差；对于频谱型地震动强度参数，ASI的有效性最好，HI的有效性最差；对于综合型地震动强度参数，Arms的有效性最好，Drms的有效性最差。

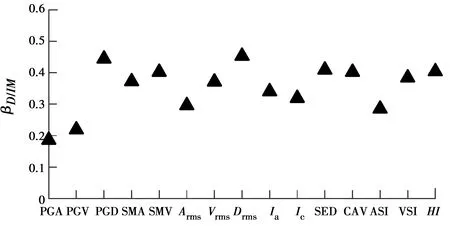
图7 地震动强度参数的有效性分析Fig.7 Efficiency analyses for the tested

4)实用性分析

实用性体现了地震动强度参数IM变化对破坏指标DI的影响大小，可用公式(3)或图5中的斜率b作为评价指标。斜率b越大，则地震动强度参数IM对结构破坏指标DI的影响越大，实用性越好；斜率b越小，则该地震强度参数IM的实用性越差。图8给出了15个IMs对应的斜率b。由图8可知，PGA的实用性最好，其斜率b最大，为0.859，PGV次之，其斜率b为0.804；Drms的实用性最差，其斜率b最小，仅为0.162，其次为PGD，斜率b为0.194。从不同IMs类型的角度，对于振幅型地震动强度参数，PGA的实用性最好，PGD的实用性最差；对于频谱型地震动强度参数，ASI的实用性最好，HI的实用性最差；对于综合型地震动强度参数，Ic的实用性最好，SED的实用性最差。

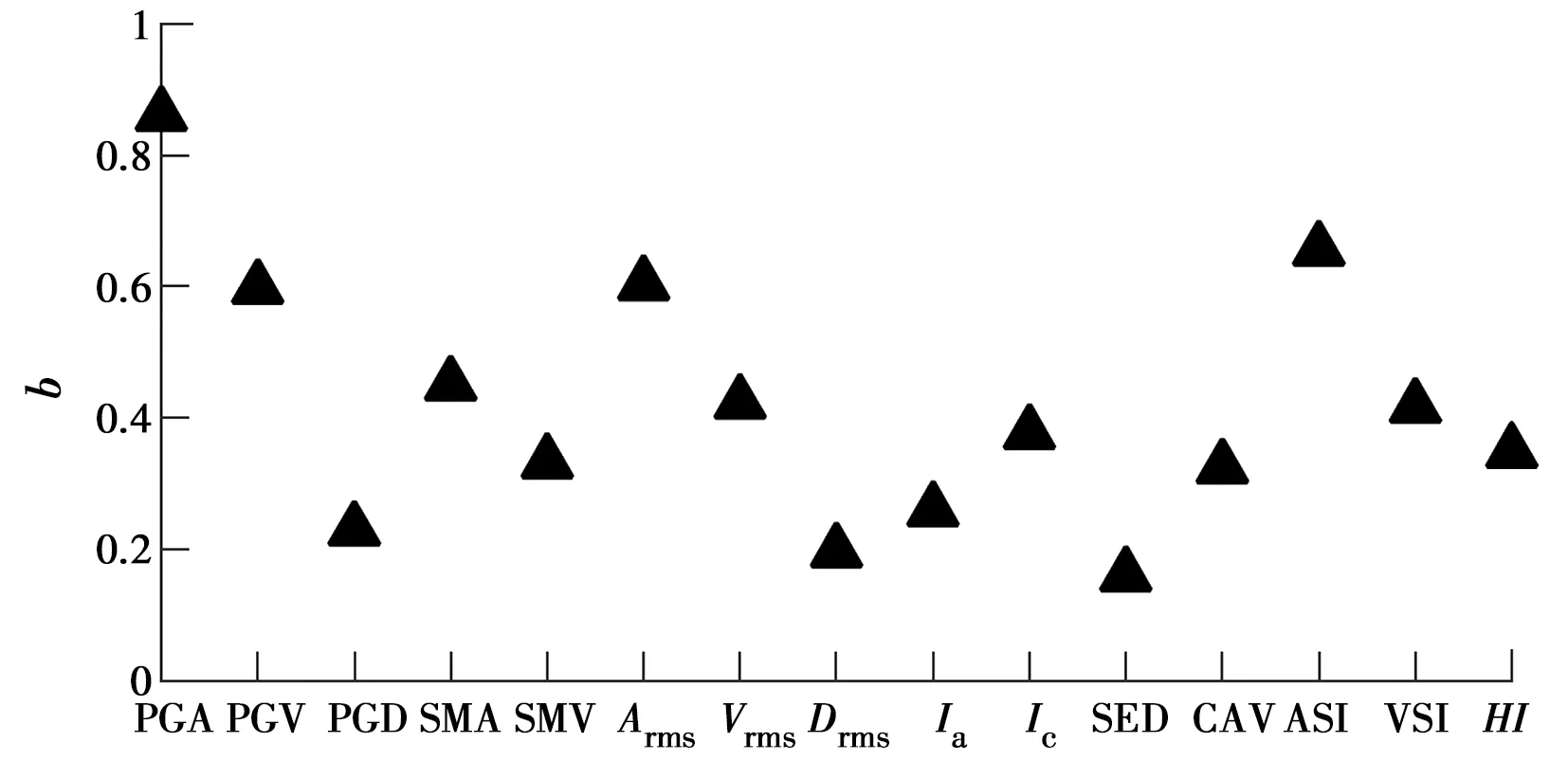
图8 地震动强度参数的实用性分析Fig.8 Practicability analyses for the tested

5)效益性分析

Padgett等[29]提出了一个能够同时考虑有效性指标βD/IM和实用性指标b的参数ζ，该参数能表达IM的效益性，其定义如式(8)所示。由式(8)可知，参数ζ越小，则该IM的效益性越好；反之，ζ越大，则该IM的效益性越差。

ζ=βD/IM/b

(8)

图9给出了15个IMs对应的效益性指标ζ。由图9可知，PGA的效益性最好，其效益性指标ζ最小，为0.216；PGV次之，效益性指标ζ为0.367。SED的效益性最差，ζ为2.556；其次为Drms，其ζ为2.311。从不同IMs类型来说，对于振幅型地震动强度参数，PGA的效益性最好，PGD的效益性最差；对于频谱型地震动强度参数，ASI的效益性最好，HI的效益性最差；对于综合型地震动强度参数，Arms的效益性最好，SED的效益性最差。

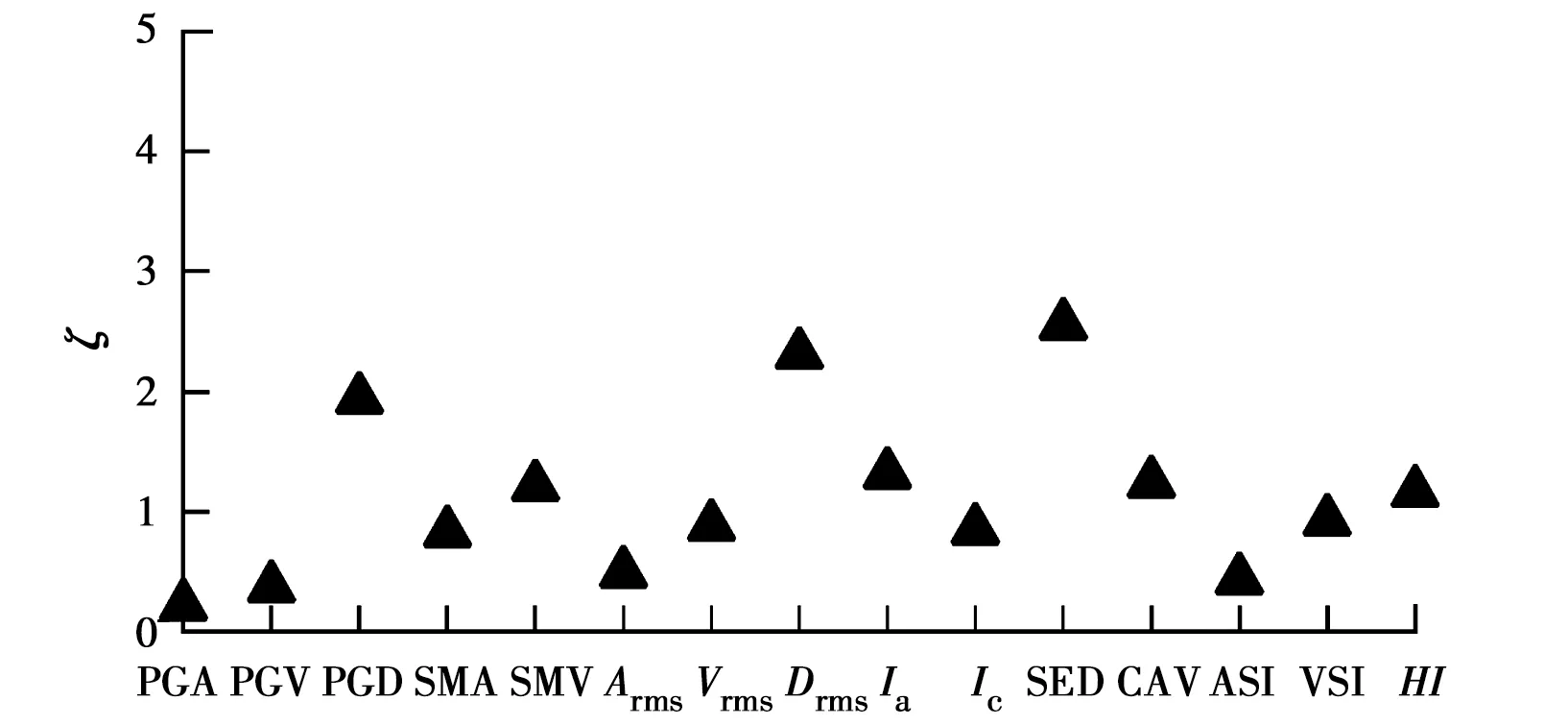
图9 地震动强度参数的效益性分析Fig.9 Proficiency analyses for the tested

6)合理标量IM

根据上述分析，表5列出了有效性、实用性及效益性中位列前3的IMs。通过对比可得，3个评价指标中位列第一的都为PGA，而PGV在有效性和效益性两项指标中均位列第二，ASI在有效性及效率性中均位列第三，而在实用性中位列第二。综上可得，PGA是软土浅埋隧道地震易损性分析中的最优IM，紧接着是PGV和ASI。

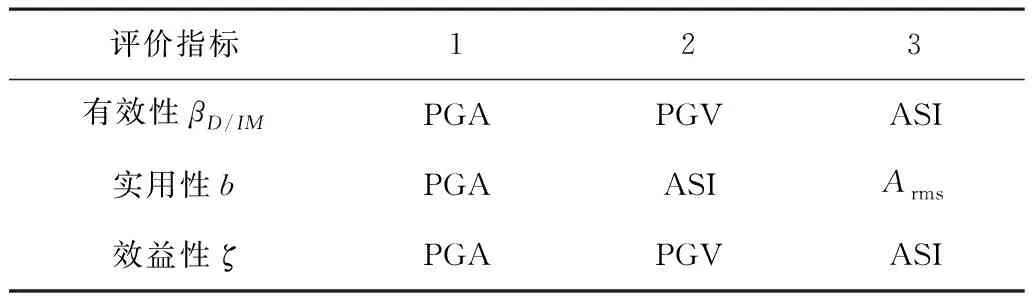
表5 排序前3位地震动强度参数IMs

由上述分析可知，PGA、PGV和ASI是浅埋隧道地震易损性分析中较为合适的地震动强度参数IM，而PGA是最优的地震动强度参数。因此，将选用PGA建立基于标量IM的地震易损性曲线，而对于基于矢量IMs的地震易损性分析，两个IMs的选择需要满足以下两个标准：IM为结构地震易损性分析合适的地震动强度参数；选取的两个IMs应属于不同类型。因此，从上述合理的地震动强度参数中选择两个较优的IMs，由上述分析可知，PGA和PGV属于振幅型IM，而ASI为频谱型IM。综合以上因素，以PGA和ASI为例，进行后续的基于矢量IMs的隧道地震易损性分析。

7)基于标量IM的地震易损性曲线

根据图6给出的PGA与DI的回归曲线及表1给出的破坏状态中值，可以分别计算得到不同破坏状态对应的易损性函数的均值λ和方差βtot，即轻微、中等及严重破坏对应的易损性曲线均值分别为0.350g、0.604g及0.968g，其方差相同，为0.533。通过上述参数，最终建立了基于标量IM的隧道易损性曲线，如图10所示。由图10可知，当PGA为0.2g时，严重破坏的概率可以忽略不计，轻微和中等破坏的概率分别为15%和2%，可知，浅埋隧道能够较好地抵抗低强度地震作用；当PGA为0.4g时，隧道发生轻微、中等及严重破坏的概率分别为60%、22%和5%；而当PGA增大到1.0g时，此时隧道发生轻微破坏的概率增至97%，而发生中等和严重破坏的概率分别增至83%和52%。

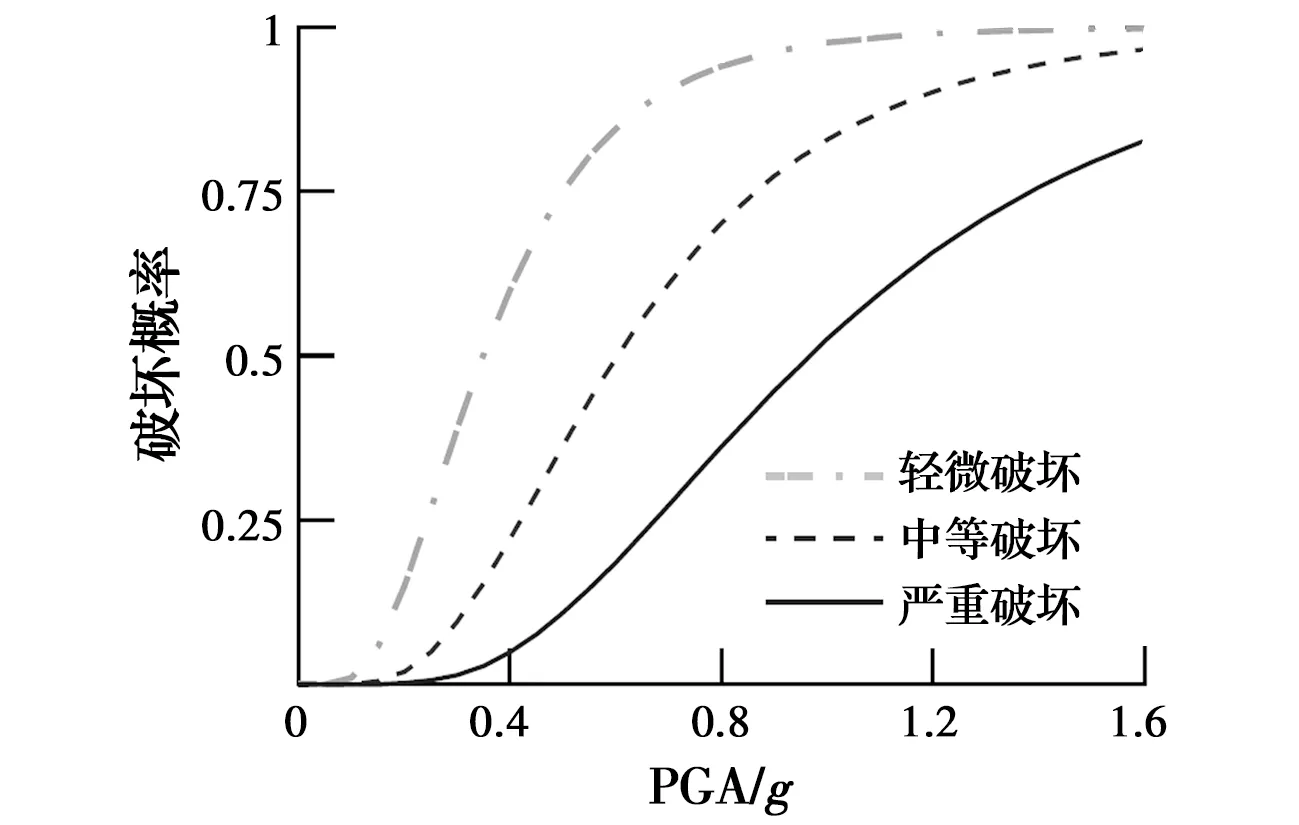
图10 建立的隧道地震易损性曲线Fig.10 Proposed seismic fragility curves of examined

3.2 基于矢量IMs的地震易损性曲面建立

1)破坏指标DI与矢量IMs的回归分析

根据选取的矢量地震动强度参数PGA和ASI与破坏指标DI进行回归拟合分析，如图11所示，其中，白点为各个破坏指标数据，网格面为回归曲面，拟合公式为

lnDI=1.147+0.739ln PGA+0.126ln ASI

(9)

由该拟合式可知，采用该组矢量IMs(PGA和ASI)得到的拟合公式相关系数为0.876，大于采用最优标量IM(即PGA)的相关系数0.859，也大于采用ASI的相关系数(0.668)。可知，在进行隧道地震易损性分析中，采用矢量IMs得到的拟合效果更好，能够显著减少对隧道破坏指标预测的离散性。

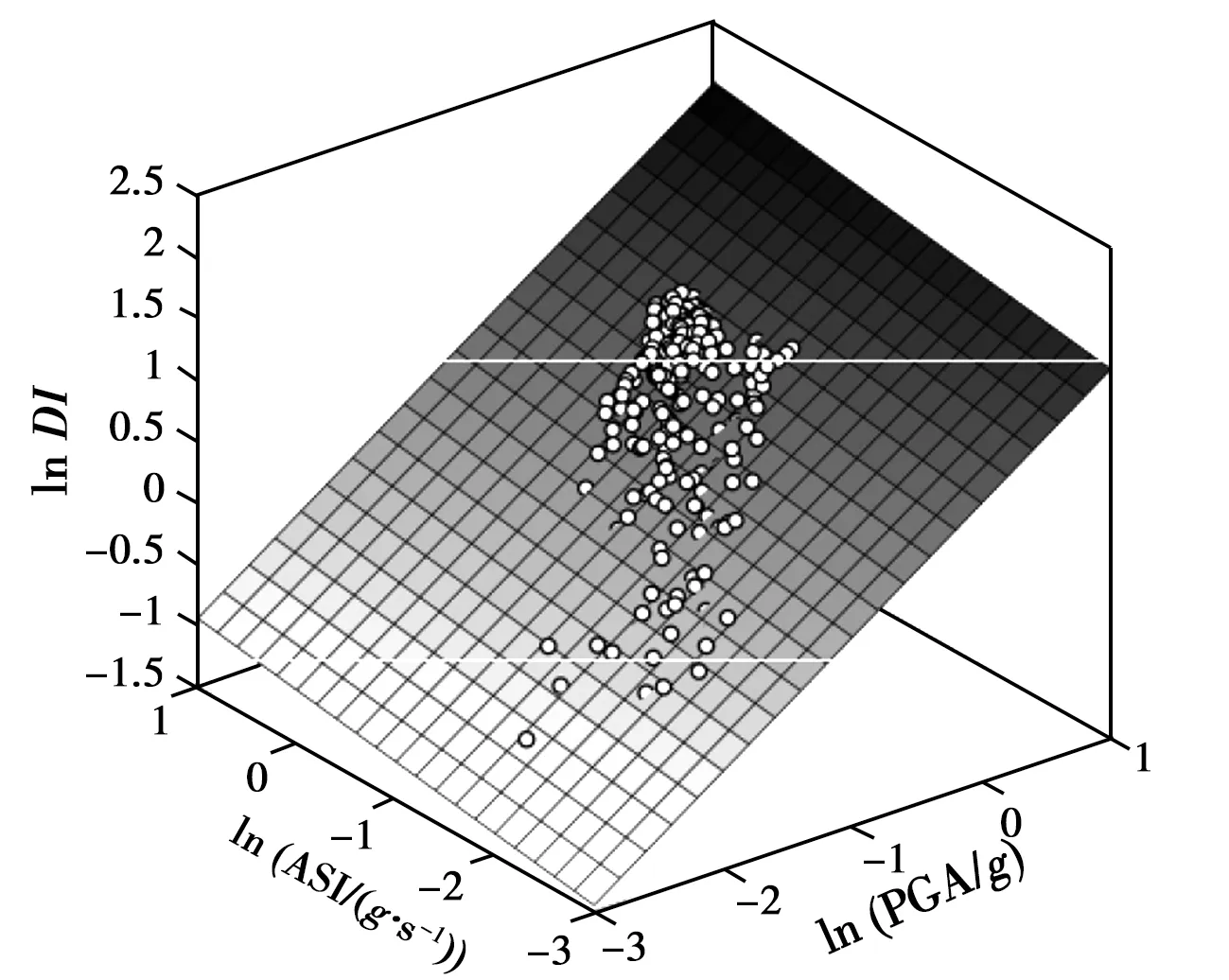
图11 破坏指标与矢量地震动强度参数的回归分析Fig.11 Regression analyses between vector-valued IMs and

2)地震易损性曲面

在确定了地震动强度参数(IM1与IM2)与破坏指标DI之间的关系后，将式(9)代入式(2)中，可以计算出当地震动强度参数IM1和IM2分别取不同值时结构超越某一结构破坏状态的概率，利用Matlab软件可以绘制出隧道在不同破坏状态下的地震易损性曲面。

图12给出了以PGA和ASI为矢量IMs的地震易损性曲面。从该组曲面中可以很方便地获得隧道在不同强度等级地震作用下发生轻微破坏、中等破坏和严重破坏的地震破坏概率，一般而言，隧道结构超越各个破坏状态的概率随IMs(PGA、ASI)的增大而增大。相对于图11给出的隧道地震易损性曲线，地震易损性曲面考虑了第2个IM对破坏概率的影响，因此，得到的易损性分析结果更为合理。

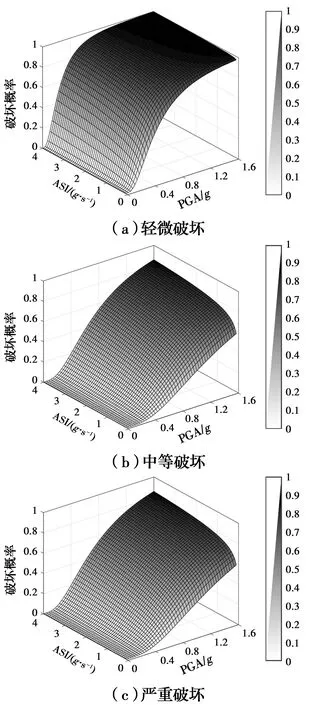
图12 建立的隧道地震易损性曲面Fig.12 Proposed seismic fragility surfaces of examined

3.3 基于标量IM与矢量IMs的计算结果对比分析

图13为以PGA为地震动强度参数的易损性曲线与以PGA和ASI为地震动强度参数的易损性曲面的对比，分别对应轻微、中等和严重破坏。图中灰色实线代表基于标量IM的易损性曲线，其余实线从基于矢量IMs的易损性曲面上获取，对应ASI分别等于0.10、0.25、0.5、1.0、1.5g·s时的曲线。

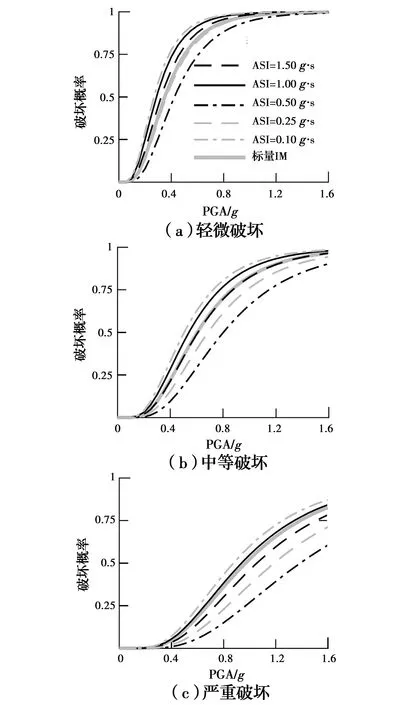
图13 易损性曲面与易损性曲线对比Fig.13 Comparisons between fragility surfaces

由图12中对比可知，采用标量IM建立的地震易损性曲线总体上都位于从易损性曲面转换得到的5条易损性曲线之间，对于每一个确定的PGA，采用标量IM的易损性曲线获得的隧道超越不同破坏状态的破坏概率为一确定值，而基于矢量IMs的易损性破坏概率则为一个区间范围。上述结果表明，基于标量IM的易损性曲线不能反映其他地震动强度参数对隧道破坏概率大小的影响，而基于矢量IMs的易损性曲面可以有效地反映由于多个地震动强度参数引起的隧道破坏概率的变化，其结果也更为精确。因此，采用矢量IMs进行地震易损性分析能够更加准确地对隧道抗震性能做出评估。

4 结论

针对软土浅埋盾构隧道展开了地震易损性分析研究，探讨了地震易损性分析中的合理IM，分别建立了基于标量IM的地震易损性曲线及基于矢量IMs的地震易损性曲面，并进行了对比，获得结论如下：

1)通过15个地震动强度参数IMs的分析对比，发现PGA是基于标量IM的隧道地震易损性分析的最优IM，其次是PGV和ASI，并利用最优IM(PGA)建立了相应的隧道地震易损性曲线。

2)在对破坏指标的回归分析中，相对于标量IM，采用矢量IMs得到的拟合效果更好，能够相对减少对隧道破坏指标预测的离散性。

3)采用最优IM(PGA)和ASI作为矢量IMs建立了隧道地震易损性曲面，可以快速地获得任意PGA和ASI下发生轻微破坏、中等破坏和严重破坏的隧道破坏概率。

4)对比发现，相较于基于标量IM的地震易损性分析，选用矢量IMs进行地震易损性分析能够有效降低对隧道地震破坏程度预测的离散性，从而可以更加精准地评估隧道的抗震性能。

5)研究结果表明，由于矢量IMs能表达更多的震动信息，相较于标量IM，在地震易损性分析中应得到更多重视，其具有重要的理论意义和广阔的应用前景。