铁路路堑高边坡的长期稳定评价方法及分级预警方法
杨甲锋,肖鹏,2
(1. 重庆铁路投资集团有限公司,重庆 400023;2. 重庆大学 土木工程学院,重庆 400045)
2020年国务院政府工作报告中提出,要重点支持既促消费惠民生又调结构增后劲的“两新一重”建设,包括:新型基础设施建设、新型城镇化建设以及交通与水利重大工程建设。铁路工程作为交通重大工程,也是“两新一重”建设的重点支持对象,对于铁路这类重大交通基础设施,在大规模的建设过程中,线路不可避免地要以深路堑形式通过丘坡地区,其地质灾害的防范与预警需求十分突出。铁路工程设计阶段通常仅考虑路堑高边坡的短期稳定性检算,而忽略了长期稳定性问题,然而路堑高边坡的长期稳定性直接影响铁路建设与运营安全。为评价路堑边坡的长期稳定性,通常在深路堑地段设置侧斜管、多点位移计、土压力盒、边坡整体GPS等自动化监测设备,以监测路堑变形、土体内部压力等参数[1-2]。土体强度、变形特性与时间的关系,即土体的流变性,包括蠕变、流动、松弛、应变率效应和长期强度效应等,土体蠕变的研究方法主要有三轴蠕变试验法及直剪蠕变试验法等[3-7]。Mesri等[8]通过一维固结蠕变试验研究构建了不同土体蠕变本构模型。由于铁路建设运营对安全和变形的要求极高,因此,有必要对路堑高边坡监测数据进行系统分析,以评估深路堑边坡的长期变形及稳定性,判断其对铁路工程的安全影响,形成合理的工程预警应对措施建议[9-10]。边坡稳定性评价分析通常采用数值模拟与理论分析相结合的方法[11-13]。然而,建立长期稳定分级评估方法时所需评价指标与时间紧密相关,在传统的边坡稳定性分析中,运用的参数不随时间改变。所以,在建立评估方法之前,需要获得长期条件下边坡安全系数与时间、位移的关系,确定稳定性分析可取的指标[14-15]。笔者利用某铁路工程路堑高边坡的长期监测数据,基于边坡变形与时间关系建立边坡长期稳定性分级评估方法,并对不同边坡提出相应的预警方法,研究结果可为类似的高边坡长期稳定性监测、评估、预警提供借鉴与参考。
1 考虑流变效应的边坡安全系数-时间-位移关系
1.1 边坡安全系数与变形关系
1.1.1 岩土体剪应力和剪应变本构模型 应力-应变的非线性关系是土的基本特性之一[16],通常可以用双曲线拟合土体三轴试验(σ1-σ3)-εα曲线数据,如图1 (a)所示。三轴试验中,如果土的应力-应变曲线近似于双曲线关系,在试验中,土的强度不可能εα达到无穷大时获得,往往以应变值εα=15%来确定;有峰值点时,取(σ1-σ3)f为峰值点强度。
因此,认为剪应力和剪应变关系依然满足双曲线模型,如图1 (b)所示。由此可得出剪应力与剪应变关系式,如式(1)所示。
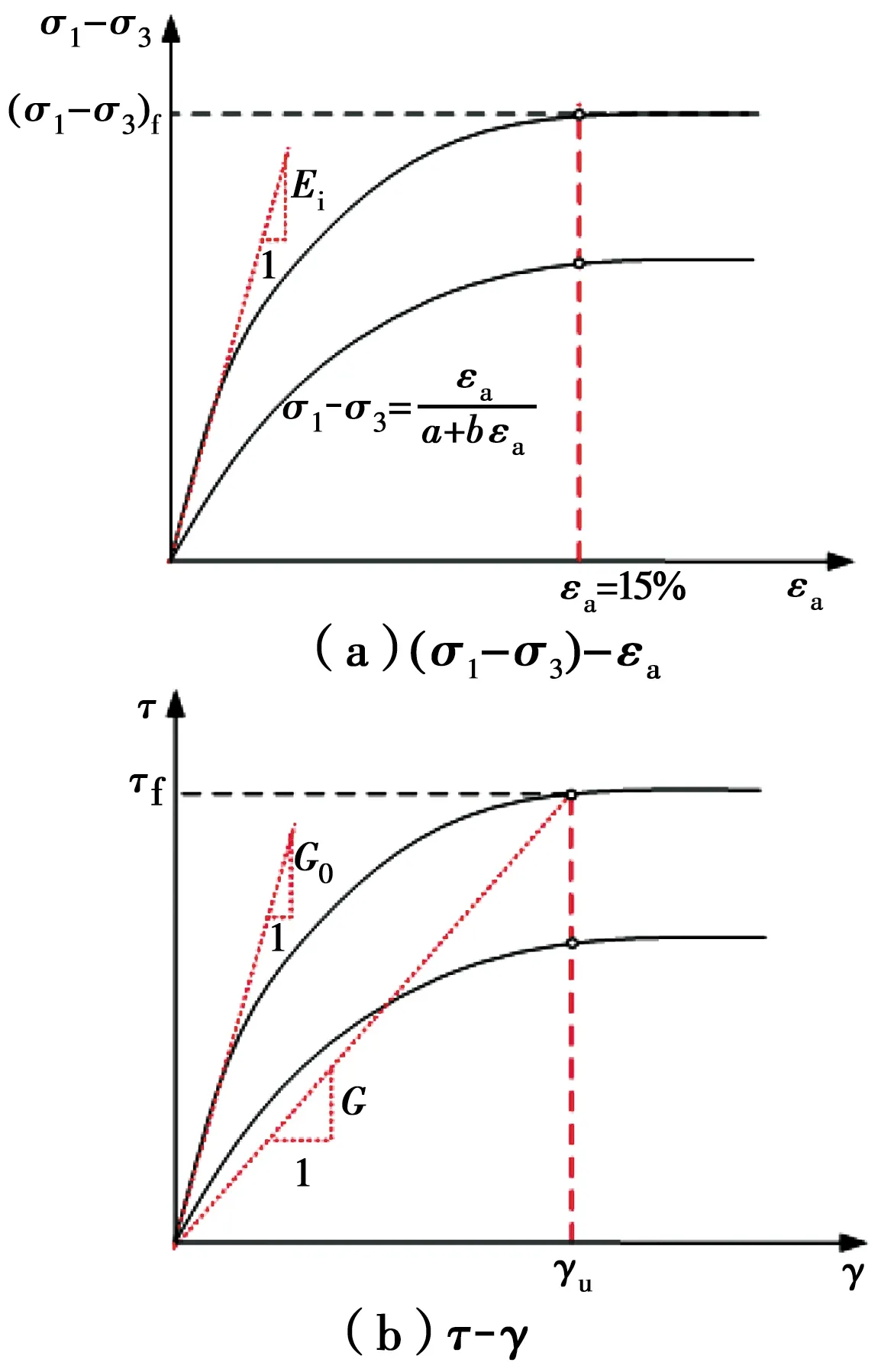
图1 剪应力-剪应变关系示意图Fig.1 Schematic diagram of shear stress-shear
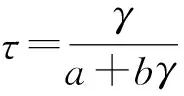
(1)
式中:a、b为待定常数,根据边界确定。将γ=γu,τ=τf代入式(1)中可得式(2)。
(2)
对式(2)求导,并令γ=0,得到式(3)。
(3)
式中:G0为γ-τ曲线的初始切线模量,假定G0与峰值剪应变时的割线模量G满足式(4)的定值倍数关系,即
(4)
式中:n为常数,可根据单剪试验确定,其值一般介于4~9之间。
将边界条件式(2)~式(4)代入式(1)中,化简可得
(5)
由此,便建立了仅含γu、τf和n三个待定常量的简化物理方程,可通过单剪试验确定。其中,n=1时,式(5)可转化为理想弹塑性模型,n=+∞时,则为理想刚塑性模型。
1.1.2 边坡安全系数与剪应变关系模型 由式(5)得单元土体安全系数Fs与剪应变γ的关系式
(6)
当n=1,即本构关系为理想弹塑性模型时,Fs与剪应变γ的关系式
(7)
当n=+∞,即本构关系为理想刚塑性模型时,当剪应变γ=0时,Fs=+∞;当γ>0时,有τf=τ,即Fs=1。
1.1.3 边坡滑动条块静力平衡方程 Fellenius法
(8)
简化Bishop法
(9)
Fellenius法和Bishop法安全系数方程与圆弧转动半径R无关,实际上是满足滑动面上切向力平衡[17]。
1.1.4 土体剪应变与坡面位移几何方程 基于单剪试验原理,发生剪应变时,剪切位移S=Dtan(γ)≈Dγ,其中,D为滑面厚度。
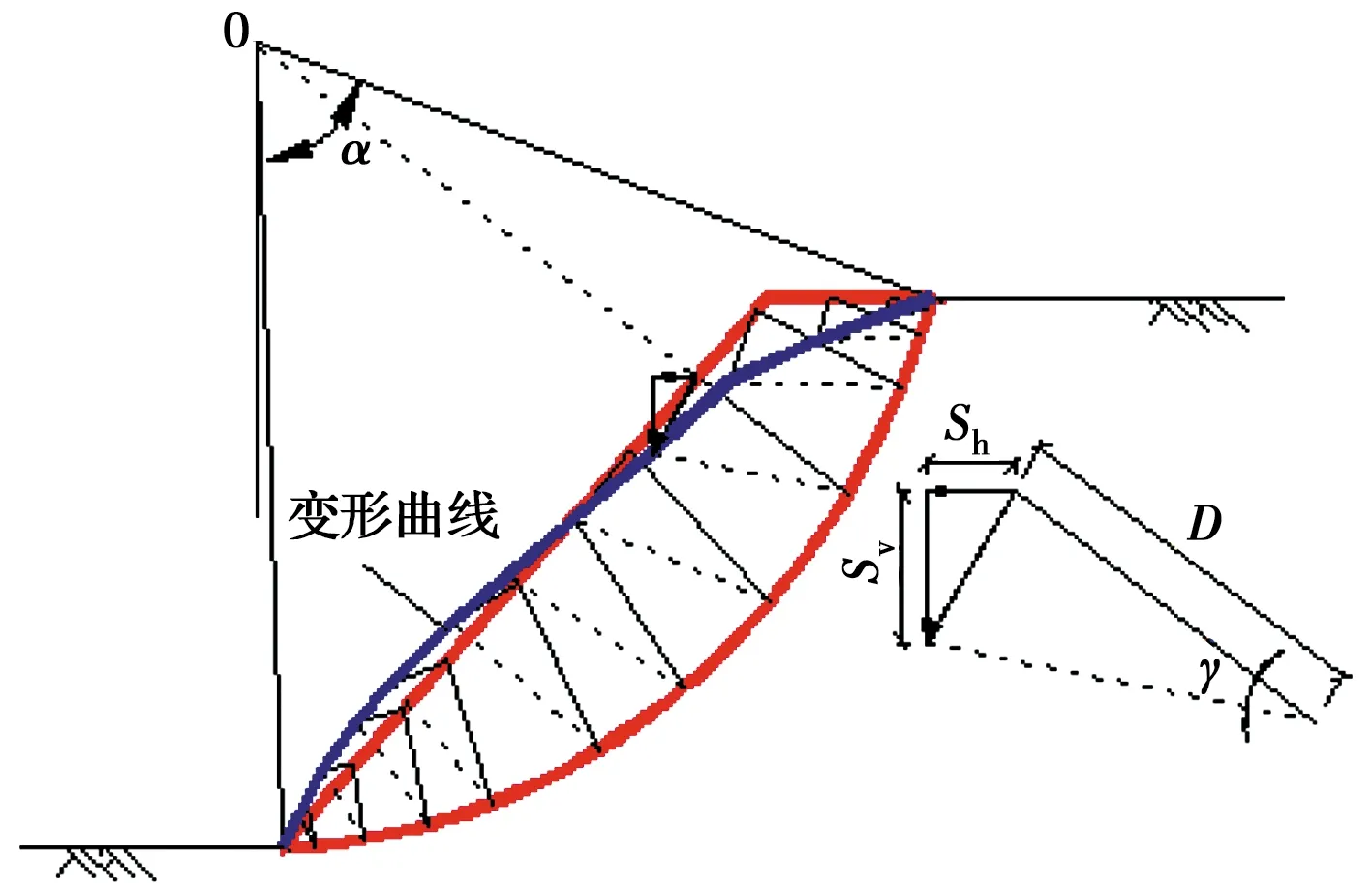
图2 土体剪应变与坡面位移示意图Fig.2 Schematic diagram of soil shear strain
因此,根据图2中的几何关系,可知坡面任一点水平位移Sh和竖向位移Sv分别为
Sh=γDcosα
(10a)
Sv=γDsinα
(10b)
1.2 岩土体长期强度与时间关系
1.2.1 对数型衰减模型 采用对数函数描述抗剪强度随时间衰减的规律,其表达式为
τt=Alnt*-B
(11)
式中:t*为剪切试验中试样破坏的时间,通常以s、min或h为单位;对于长期强度,因考虑建筑物或结构物的有效期或设计期限t,通常以a为单位,故t>t*。因此,定义时间比尺参数t*=t/T。如果试验过程t*以min为时间间隔,为获得以a为单位表示的结果数据,则T=1/(365×24×60),故由式(11)得
τt=Alnt-AlnT-B
(12)
因此,长期强度τlong为
τlong=Alntlong-AlnT-B
(13)
式中:tlong为长期强度对应的时间,或建筑物、构筑物使用期限,按式(14)确定。
(14)
将式(14)代入式(13),得
tlong=exp(1.03ln 100+0.03B/A-0.03T)
(15)
由此,要确定强度随时间的变化关系,只要获得A、B两个参数即可,严格的做法需要开展不同历时下的蠕变试验。在缺乏蠕变试验数据时,可采用估算方法确定。令不同土质的长期强度满足式(16)。
τlong=λτ0
(16)
式中:τ0为瞬时强度,可由室内试验测得;λ大小与土性相关,取值范围一般介于0.65~0.75之间,取0.7。由于瞬时强度也满足式(12),故得
τ0=Alnt0-AlnT-B
(17)
由式(3)、式(12)~式(17)联立可解得A、B为
(18)
因此,只需要获得瞬时强度及对应的时间即可确定长期强度衰减曲线。
1.2.2 双曲线型衰减模型 根据强度与时间变化规律,可以采用抗剪强度随时间增长而降低的双曲线函数进行描述,其表达式为
(19)
式中:A′、B′、C′为拟合参数。
当t→∞时,长期强度τ∞→A′-B′,即双曲线衰减模型以长期强度为渐近线。当t→0时,长期强度τ0→A′,即A′为瞬时冲击强度。
可根据试验测得上述3个参数。在缺乏试验数据时,也可根据直剪试验测得的剪切时间与强度值(t0,τf0)和经验关系式τ∞=λτf0,以及(τ∞-τ100)/τ100=δ%等3个已知条件,代入式(19)可以确定该式中的3个参数A′、B′、C′的值,分别用A*、B*、C*表示。
强度对数型衰减模型和双曲线型衰减模型的区别在于:当t→0时,前者趋于无穷大,后者趋于固定值;t→∞时,前者强度值趋于无穷小,后者存在渐近线。在短期内,两个模型都能很好地描述强度的衰减特性。
1.3 边坡安全系数-时间-位移关系
1.3.1Fs-t关系 由式(12)和式(17)得出抗剪强度方程为
(20)
令B/A=η,式(20)变为
(21)
由此得出强度随时间变化的衰减系数λt
(22)
由此定义瞬时安全系数为
(23)
式中:τf0为单剪试验测得的抗剪强度。
因危险滑面上的剪应力τ与时间无关,由式(23)得
(24)
由此可得安全系数Fst随时间t的变化关系式
(25)
1.3.2 边坡破坏区γ-t关系及坡面位移S-t关系 由式(6)得安全系数Fst和剪应变γ的关系式为
(26)
将式(25)代入式(26),得出剪应变γ与时间t的关系式
(27)
将式(10a)、式(10b)分别代入式(27),得坡面水平位移Sh和竖向位移Sv与安全系数Fst的关系式
(28)
由此,矢量位移S与时间t的关系式
(29)
因此,由式(25)和式(29)即可计算出安全系数-时间-位移关系。其中,衰减系数λt方程由对数型强度模型导出;若采用双曲线型强度模型,式(25)和式(29)λt调整为
(30)
式(29)中,极限剪应变γu可以通过试验测得。刘斯宏等[18]通过大型单剪切试验测得粉砂质泥岩堆石料在法向压力200 kPa时极限剪应变处于2%~5%之间,刘平等[19]认为,在没有峰值时,坝体堆石料的剪应力-剪应变曲线中,剪应变一般取5%,有峰值时,取峰值剪应力对应的剪应变。同时,极限剪应变γu并不是固定常数,而是与土的性质、密实度与潮湿状态、法向压力等因素密切相关。
2 高边坡长期稳定评价指标与风险分类分级预警
2.1 高边坡长期稳定评价指标
2.1.1 长期稳定安全系数F∞边坡安全系数的降低是土体抗剪强度衰减所致,然而土体抗剪强度衰减主要有两个因素:1)长期强度特性;2)降雨等环境影响。前者体现单元土体抵抗破坏的能力随加载时间的延长而降低,反之,要求对于永久边坡,瞬时加载土体强度最高;后者是土体遇水软化效应。对于永久边坡,《铁路路基设计规范》(TB 10001—2016)[20]要求一般工况安全系数不低于1.15~1.25,实质上该安全系数是由抗剪强度试验(快剪、固结快剪、慢剪)测得的强度指标换算而来的瞬时稳定安全系数,并未考虑岩土体蠕变特性,也就是未考虑到岩土体的长期强度。从剪切蠕变试验可知,荷载水平λ超过70%时,土体处于缓慢破坏状态,按照安全系数定义,此时Fs低于1.43,虽满足设计规范中不低于1.15~1.25的要求,但边坡此时却处于缓慢破坏状态。因此,采用瞬时安全系数评价边坡长期稳定不合适,应采用与边坡蠕变时间相关的长期稳定安全系数Fst,图3给出了荷载水平、瞬时安全系数Fs和长期安全系数Fst的关系。
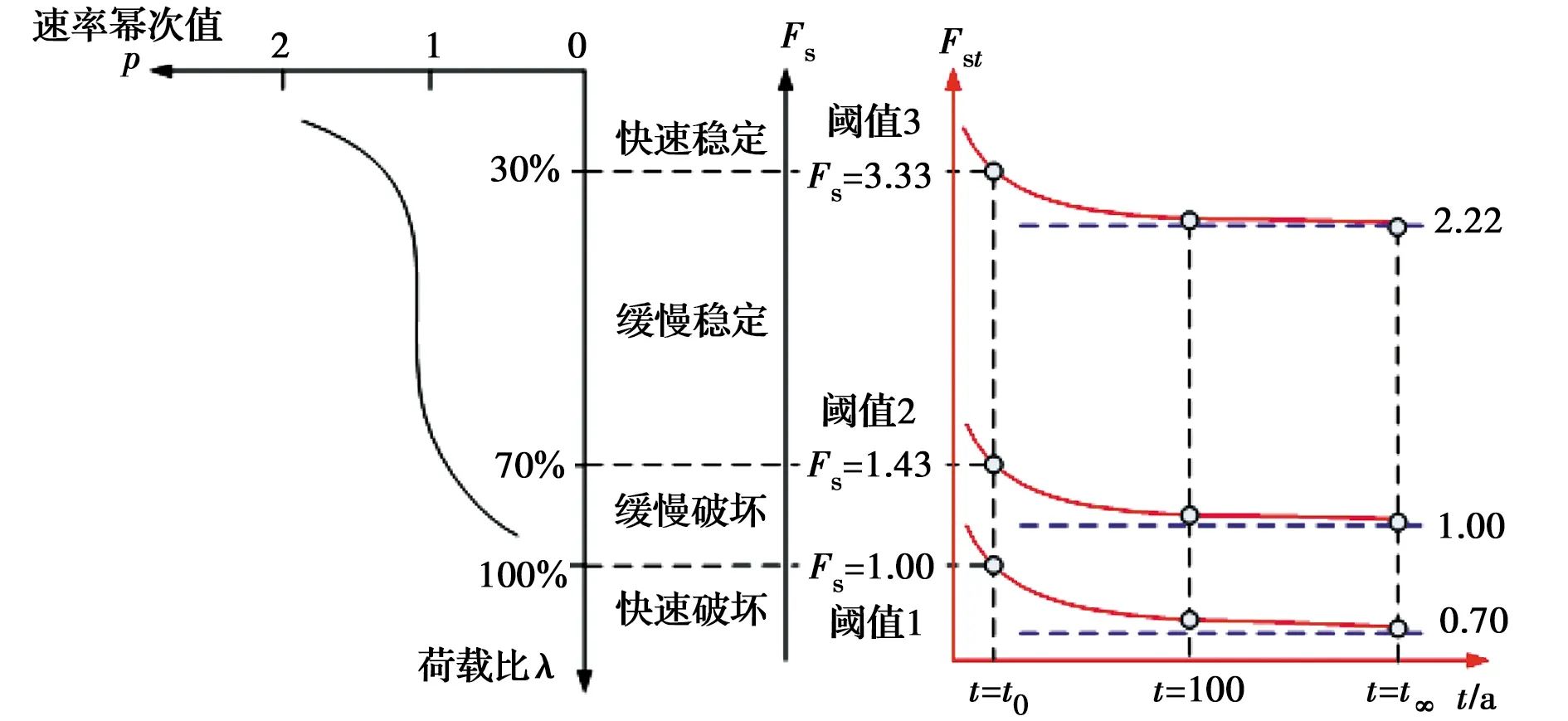
图3 边坡瞬时与长期稳定安全系数关系及状态阈值Fig.3 Relationship between transient and long-term stability safety factor of slope and the state
从图中可以看出,边坡处于快速稳定、缓慢稳定、缓慢破坏、快速破坏4种状态区域对应的安全系数Fs阈值分别为3.33、1.43、1.00,长期稳定安全系数F∞阈值分别为2.22、1.00、0.70。
2.1.2 变形速率幂次值p上述长期稳定安全系数评价指标虽然反映了岩土体的长期强度特性,但未考虑不利降雨等环境因素的影响,当遇到不利环境因素时,边坡变形速率和位移均会发生响应。因此,长期稳定状态评价还需考虑边坡变形速率,即通过速率幂次判别准则进行边坡状态评价。由图3可见,快速稳定、缓慢稳定、缓慢破坏、快速破坏4种状态区域对应的速率幂次p值分别为2、1、0。
2.1.3 位限指数SL图4给出了坡面位移随时间的变化关系,通常,变形速率由缓慢破坏至最终破坏可能需数十年甚至上百年,这与土质条件相关。但如果位移初值就比较大,或者实测位移已接近极限位移,即便变形速率未达到快速破坏界限值,也是一个十分危险的信号。因此,变形稳定尚需附加一个重要指标,即位限指数SL,其计算式为
(31)
式中:Sf为破坏位移,即极限位移;Sm为测试中值;S0为瞬时变形。
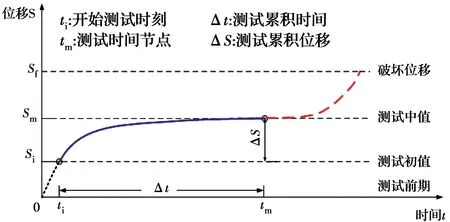
图4 坡面位移与时间变化关系曲线Fig.4 Variation curve of slope displacement and
图中Si为测试初值,即测试开始时,已经发生但尚未测得的位移。从图4中可以看出,测试累积位移为ΔS=Sm-Si,将其代入式(29),得到ΔS与时间Δt的关系式
ΔS=Sm-Si=
(32)
ΔS=Sm-Si=
(33)
式(32)和式(33)分别为强度对数衰减模型和双曲线衰减模型下的两种表达式。在已知参数n、γu、t0、τ0和已知条件A′=τ∞+B′、τ∞=λτ0的情况下,式(33)中仅有C′、D、γi三个参数待定,可通过现场变形观测数据进行拟合确定。
位限指数SL表示位移发展的相对大小,最大值为1,如超过1即为已发生滑动破坏。因此,通过边坡位限指数SL将边坡变形程度划分为微变形、小变形、中变形、大变形,其取值标准如表1所列。

表1 边坡变形程度界定方法
综上,路堑高边坡长期稳定评价3个指标依次为:长期稳定安全系数F∞、变形速率幂次值p和位限指数SL。
2.2 高边坡风险分类分级预警方法
2.2.1 高边坡安全稳定四级预警方法 根据变形速率幂次值p与位限指数SL对边坡变形速率及边坡变形程度的界定,将边坡安全稳定预警信号分为4级,分别用绿色、黄色、橙色、红色表示。四级预警方法是依靠现场变形观测数据分析的位移监测速率幂次值p与位限指数SL得出,SL以边坡变形程度为依据分为4类,p以边坡变形速率为依据分为4类。各级预警标准如表2所示,分别为:一级绿色预警位于表中左下角,其标准为:位移监测速率幂次值p≥2且位限指数满足0≤SL<0.5,或者1≤p<2且位限指数满足0≤SL<0.25;四级红色预警位于表中右上角,其标准为:位移监测速率幂次值p<0且位限指数满足0.5≤SL<1.0,或者0≤p<1且位限指数满足0.75≤SL<1;二级黄色预警位于主对角线下方与一级绿色警戒上方之间,其标准为:位移监测速率幂次值0≤p<1且位限指数0≤SL<0.25,或者速率幂次值1≤p<2且位限指数0.25≤SL<0.5,或者速率幂次值p≥2且位限指数0.5≤SL<0.75;三级橙色预警位于主对角线上方与四级红色警戒下方之间,其标准为:位移监测速率幂次值p<0且位限指数满足0.25≤SL<0.5,或者速率幂次值0≤p<1且位限指数满足0.5≤SL<0.75,或者速率幂次值1≤p<2且位限指数满足0.75≤SL<1。表2中,主对角线是二级黄色预警的预警分界线,考虑到铁路路堑高边坡破坏对线路工程设施及列车安全运行影响较大,需加强对高边坡安全稳定性的监测。四级预警方法主要反映高边坡短期和中期稳定情况,适用于只依靠现场变形观测数据条件下进行的风险初判,可作为直观预警预报参考。
2.2.2 高边坡安全稳定八级预警方法 八级预警方法是在四级预警方法的基础上考虑了安全系数指标对高边坡长期稳定性的影响,将安全系数Fs纳入四级预警方法,形成八级预警方法,Fs以高边坡长期稳定程度指标为依据分为4类。八级预警方法是在四级预警参数基础上,对结合稳定性分析软件计算获得的长期稳定安全系数进行精细评判,实现对高边坡短期、中期与长期评价,使预警方法更加全面、精准、可靠。
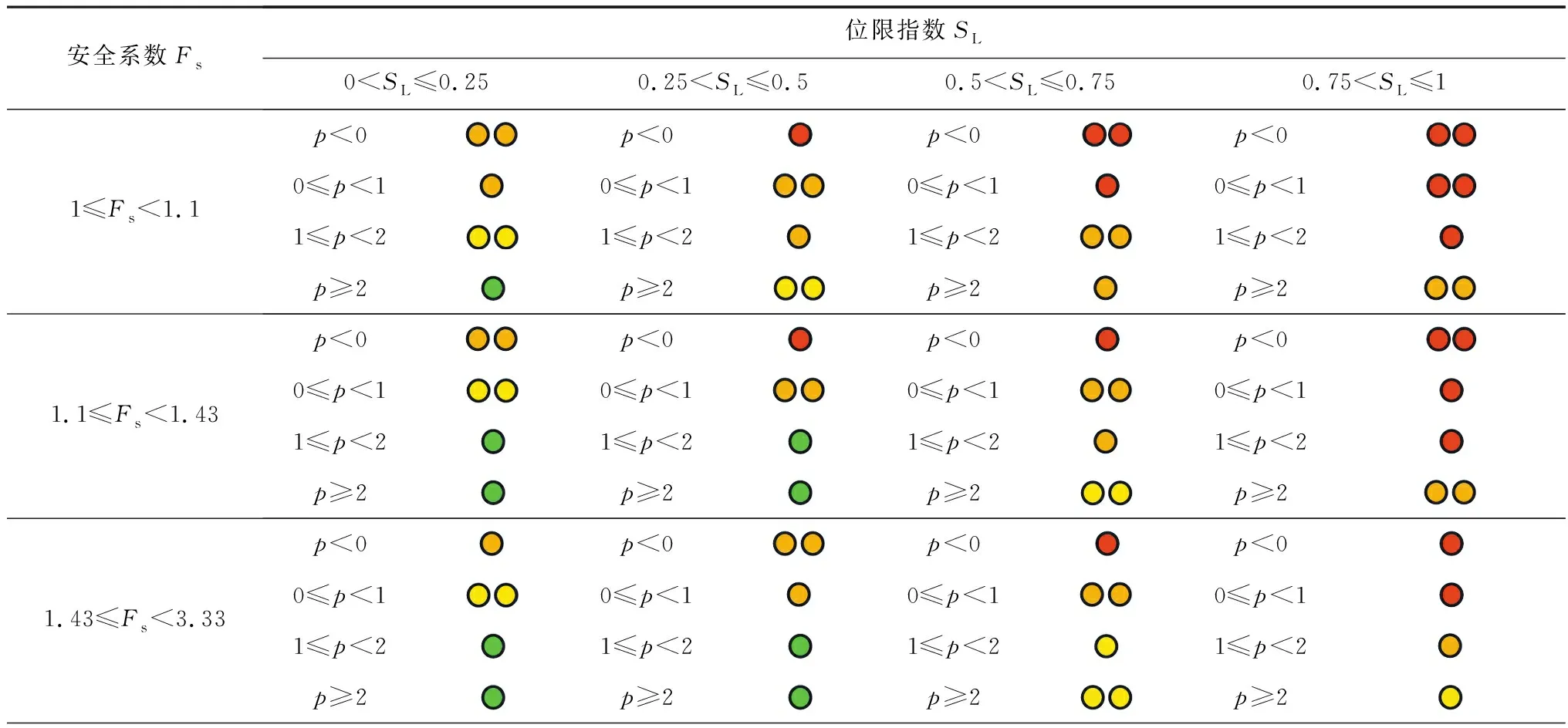
表3 高边坡安全稳定八级预警方法
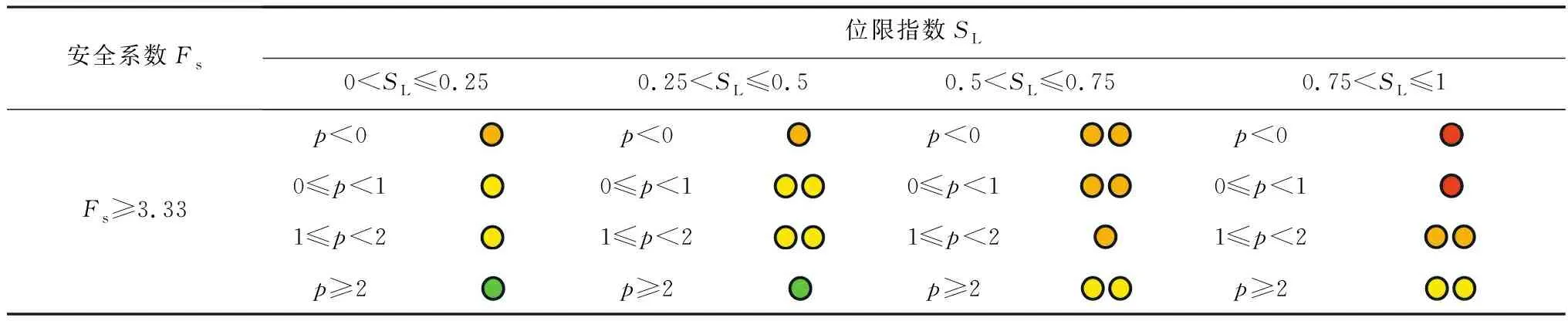
续表3
表4详细阐述了表2与表3中信号指示灯颜色的具体含义。表中从左至右危险等级逐渐升高,警戒程度逐级加强。
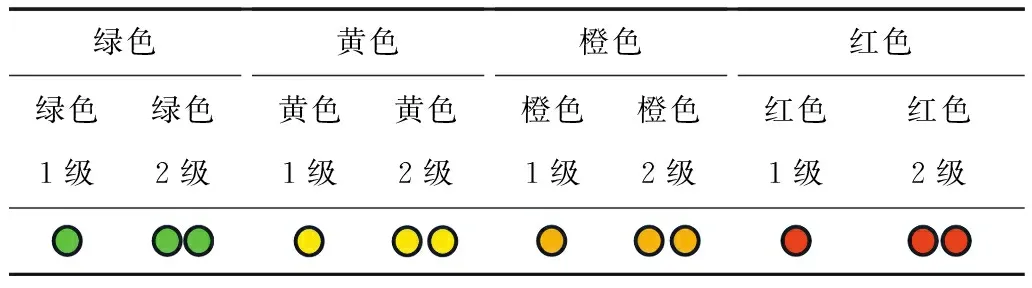
表4 信号指示灯含义
工程中,可根据不同信号颜色进行预警,以确保列车安全运行,预警级别与报警信号对应关系如表5所示。绿色信号定义为“警消级”,表示无任何危险征兆,可取消预警信号;黄色信号定义为“警示级”,表示需密切关注变形速率及位限指数变化;橙色信号定义为“警戒级”,表示已有明显危险征兆,此时须加强监测密度、跟踪预报,并采取加固措施降低其警示级别;红色信号定义为“警鸣级”,表示已发生危险情况,此时列车必须停止运行,并紧急疏散现场监测人员,启动报警器。

表5 预警级别及其方式
3 高边坡长期稳定评价方法及预警方法的工程应用
针对某铁路路堑高边坡,利用现场布设的监测点得到的位移与时间关系数据,结合提出的高边坡长期稳定性评价方法对该高边坡进行评估,计算其3个长期稳定性评价指标,最后确定对应风险分级预警方法。
3.1 瞬时稳定安全系数分析
图5为所研究高边坡的几何概化模型。土质条件为上层硬塑黄土、下层坚硬黄土。一级边坡采用坡面墙防护措施,从坡脚至坡顶共设置了8处位移监测点,坡高H=42 m。具体布置如图5所示。
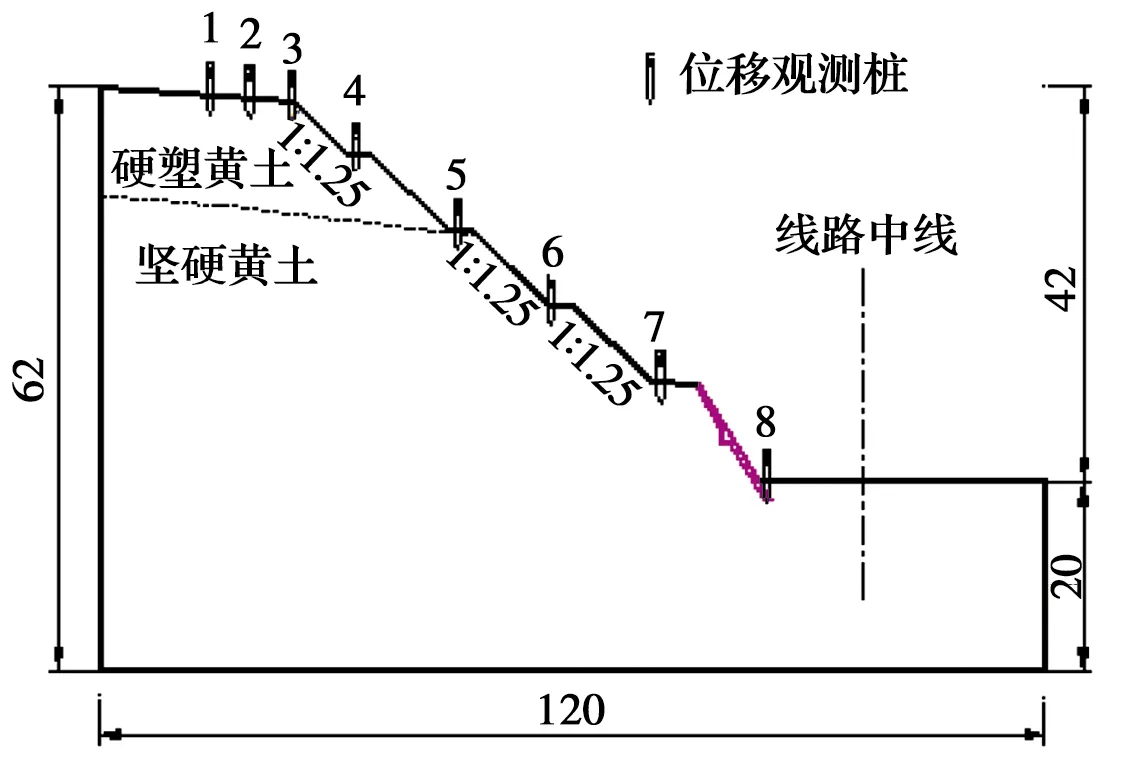
图5 典型断面路线高边坡概化模型(单位:m)Fig.5 Generalized model of typical section route
稳定分析计算应用geostudio软件[21],分别采用瑞典法、简化Bishop法、M-P法和简化Janbu法等刚体极限平衡法进行安全系数计算,结果如表6所列。

表6 安全系数计算结果
边坡工程设计中,常采用瑞典法和Bishop法两种方法对其进行稳定性评价。瑞典法由于不考虑条件作用力,使得所得安全系数偏小;而Bishop法考虑了条间法向力,所得安全系数与具有严格条分意义的M-P法较为接近,能近似反映土体底部法向应力或土体底部抗力。因此,对于圆弧滑动模式的均质边坡,以Bishop法所得安全系数为代表值,反映滑面上任一土体抗剪强度与剪应力的比值。
3.2 长期稳定安全系数分析

表7 各参数取值结果
根据表7中参数,采用边坡安全系数与时间关系模型,可获得安全系数Fst-t关系曲线,如图6所示。

图6 高边坡安全系数与时间变化关系曲线Fig.6 Relation curve of high slope safety
由图6可知,边坡稳定安全系数随时间发展而逐渐降低,最终趋于稳定。在λ=0.7时,按照Bishop法计算得出长期稳定安全系数F∞=1.372,说明该高边坡具有长期稳定性。
3.3 长期累积变形状态分析
3.3.1 位移与时间关系分析 分别选取坡顶处测点1、坡中部测点6、坡脚处测点8为边坡总体变形发展情况的代表测点。图7为测点1相应矢量方向位移随时间变化的关系及位移-时间拟合关系,拟合曲线能良好地反映位移随时间的变化关系。同理,测点6、测点8的位移-时间拟合结果也较好。具体拟合参数如表8所示。
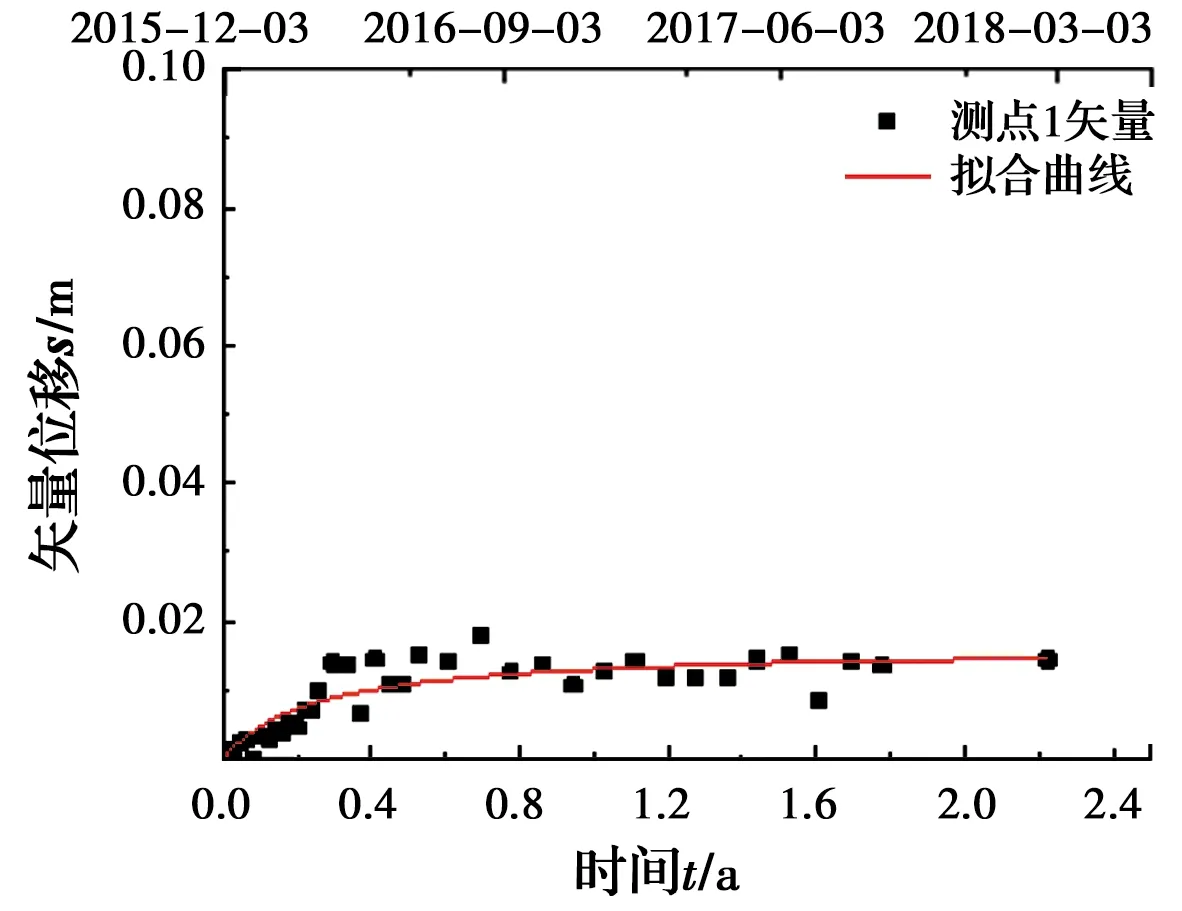
图7 测点1位移与时间变化关系曲线Fig.7 Relation curve of displacement and time history

表8 测点1、6、8位移-时间曲线拟合参数值
由表8可以看出,边坡3个代表点测得的位限指数SL在0.34~0.36间小幅变化,平均值为0.35,处于0.25 3.3.2 变形速率与时间的关系分析 图8为测点1、6、8处边坡矢量方向位移及变形速率随时间的变化情况。因速率变化实测数据存在明显围绕横坐标轴上下波动的特点,体现在累积位移减小与增大的交替变化上。总体上,各测点变形速率呈现衰减的变化特征,而且在前期衰减最为迅速,后期逐渐趋于0。 图8 变形速率与时间关系曲线Fig.8 Relation curve of deformation rate and time 采用幂函数速率曲线数据进行拟合,得到幂函数的两个系数,结果如表9所示。从表中可知,边坡不同位置处变形速率幂次值p均大于1,平均值为1.65,表明该路堑高边坡处于缓慢稳定状态。 表9 变形速率与时间的关系拟合参数 通过长期稳定安全系数F∞、位限指数SL、变形速率p值3个指标来评价高边坡的长期稳定性。其中,Fs100反映高边坡长期强度发挥水平、SL反映位移变化发展程度、p值反映变形速率收敛快慢,3个指标计算结果如表10所示。表中位限指数SL、变形速率p值取坡顶、坡中、坡脚3处测点平均值。 表10 长期稳定安全评价指标值 按八级预警方法评价可知,该断面边坡长期稳定安全系数F∞=1.372,位移监测速率幂次值1≤p<2且位限指数0.25 基于铁路路堑高边坡稳定性问题,系统研究了边坡岩土体变形时间效应与安全系数、边坡安全系数与剪切变形及长期强度的内在关系,形成了高边坡长期稳定评价指标及分级预警方法。得到如下主要结论: 1)根据剪切流变试验中剪应力水平μ=τ/τf与安全系数Fs的倒数关系,得到土体变形演化不同状态剪应力水平阈值及对应的安全系数Fs,确定不同边坡安全系数Fs对应的变形状态。 2)建立综合反映土体应力-应变特性影响的边坡位移-安全系数函数关系。在此基础上,考虑岩土体的长期强度影响因素,构建了安全系数-剪切变形-时间的关系模型。 3)综合考虑边坡设计安全系数、位移发展程度和变形速率变化特征,提出路堑高边坡长期稳定3指标评价方法,即长期稳定安全系数F∞、位限指数SL和变形速率幂次值p。 4)基于路堑高边坡长期稳定控制指标,提出两种高边坡风险分级预警方法,根据不同预警等级明确了不同等级下应该采取的应急处理措施。 5)通过对实际铁路工程中高边坡的长期位移监测数据分析,应用稳定3指标评价方法进行评价并确定其风险预警分级,为类似工程的长期稳定评价及预警分析提供参照。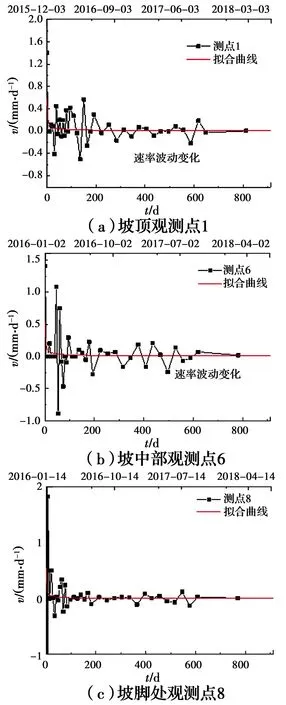


4 结论

