基于证据权和卡方自动交互检测决策树的滑坡易发性预测
黄发明,石雨,欧阳慰平,洪安宇,曾子强,徐富刚
(南昌大学 建筑工程学院,南昌 330031)
如何有效开展滑坡易发性预测制图是现阶段全世界范围内区域滑坡研究的重点和难点。通过将GIS与数据驱动模型相结合,以图像和数字的方式可构建出更高效准确的易发性预测模型。该易发性制图的思路对滑坡高发地区的防灾减灾规划具有重要意义[1]。
滑坡易发性可定义为特定地点在环境因子非线性耦合作用下发生滑坡的空间概率。基于地理相似性规律,即“地理环境越相似,地理特征越相近”可知,通过已经发生滑坡的环境因子来建立预测模型,则潜在滑坡的空间位置有可能被预测[2]。很明显,从滑坡样本点中确定滑坡易发性与其环境因子的关系式是易发性预测的关键所在,因此,选择用以获取输入变量的滑坡-环境因子关联分析法非常重要。随着遥感和GIS等基础数据源获取技术的进步,易发性建模的空间数据源及其质量有了较大提升[3]。一般而言,具体研究区内的滑坡环境因子类型可通过相关文献综述和研究区的自然地理和地质条件确定。笔者重点关注滑坡易发性建模过程中滑坡与其环境因子的非线性关联分析这一不确定性因素,并进一步研究其对滑坡易发性建模的影响。
启发式模型、数理统计模型和机器学习模型是易发性预测过程中常用的3种类型[4]。启发式模型[5]和数理统计模型被大量使用,主要有确定性因子(Certainty Factors,CF)[6]、层次分析法[7]和多元线性回归[5]等;机器学习相关模型包括逻辑回归(Logistic Regression,LR)[8]、C5.0决策树[9]、人工神经网络[10-11]、随机森林(Random Forest,RF)[12]、支持向量机(Support Vector Machines,SVM)[13]、卡方自动交互检测(Chi-squared Automatic Interaction Detector,CHAID)决策树[14]和贝叶斯网络[15]等。对于哪种类型的模型最适合易发性预测,现阶段还没有一致的意见,但优秀的机器学习模型能够提高滑坡易发性预测精度,对滑坡易发性区间划分有着显著影响,并可能进一步改变滑坡易发性级别的划分。笔者拟用CHAID决策树这一被广泛应用的典型机器学习方法构建滑坡易发性模型并探索建模不确定性特征。
在将建模预测出的滑坡易发性指数(Landslide Susceptibility Index,LSIs)与各类环境因子开展联系时,需开展滑坡与其基础环境因子(不考虑诱发因子)之间的非线性关联分析,其关联值可直接作为易发性模型的输入变量[16]。目前,常用的关联分析法包括确定系数[17]、频率比(Frequency Ratio,FR)[18]、熵指数(Index of Entropy,IOE)[16]和证据权重(Weight of Evidence,WOE)[19]等。不同关联分析法的内部计算思路具有较大的差异性,导致各方法下的易发性建模存在不确定性[20-21]。关联分析法太粗糙会导致部分信息丢失,降低模型预测精度;优秀的关联分析法能获取较准确的环境因子影响滑坡发育的信息,进一步提高滑坡环境因子分析及其建模的可靠性。可见,探讨不同关联分析法对易发性预测建模的影响规律具有重要意义。
学者们采用不同关联分析法和模型开展易发性预测建模,例如:Zhang等[22]应用IOE模型、LR-IOE和SVM-IOE模型获得了中国陕西省府谷县滑坡易发性图,结果表明,LR-IOE模型的准确率最高,其次是IOE模型和SVM-IOE模型。李文彬等[23]深入探讨滑坡与其环境因子间的非线性联接以及不同数据驱动模型对滑坡易发性预测建模不确定性的影响规律,结果表明,RF模型预测性能最优,WOE-RF模型预测的滑坡易发性不确定性较低。张钟远等[24]基于地理信息系统平台构建了云南省镇康县滑坡易发性预测指标体系,结果显示,频率比耦合LR模型具有更高的成功率和预测率。但大多数情况下,现有研究使用特定的关联分析法开展易发性预测建模,而较少提供可信的依据和合理的解释,并且较少深入探讨这种不确定性因素对易发性预测建模的影响。通过探讨关联分析法耦合模型下的滑坡易发性结果的不确定性,更能深入理解易发性预测的可靠性和可行性,可降低关联分析法不确定性因素带来的影响。
笔者采用FR和WOE两种非线性关联分析法的计算数据值与原始环境因子数据(以下简称“原始因子数据”)作为CHAID决策树模型的输入变量,以陕西省延长县为例,开展滑坡易发性预测建模的不确定性分析,包括精度评价、LSIs分布规律和平均秩等。
1 滑坡易发性建模分析
FR和WOE两种关联法耦合CHAID决策树模型时的易发性预测建模流程(图1)如下:
1)获取研究区滑坡编录及相关环境因子数据源以便构建易发性建模的空间数据集;
2)将FR、WOE和原始因子数据作为CHAID决策树的输入变量,形成3种耦合模型;
3)分别对3种耦合模型开展易发性预测建模,然后在GIS中绘制滑坡易发性图并划分易发性等级;
4)通过ROC精度、均值、标准差和平均秩等对易发性预测结果进行不确定分析;
5)通过对比分析找到最佳关联分析法,为易发性建模提供指导。
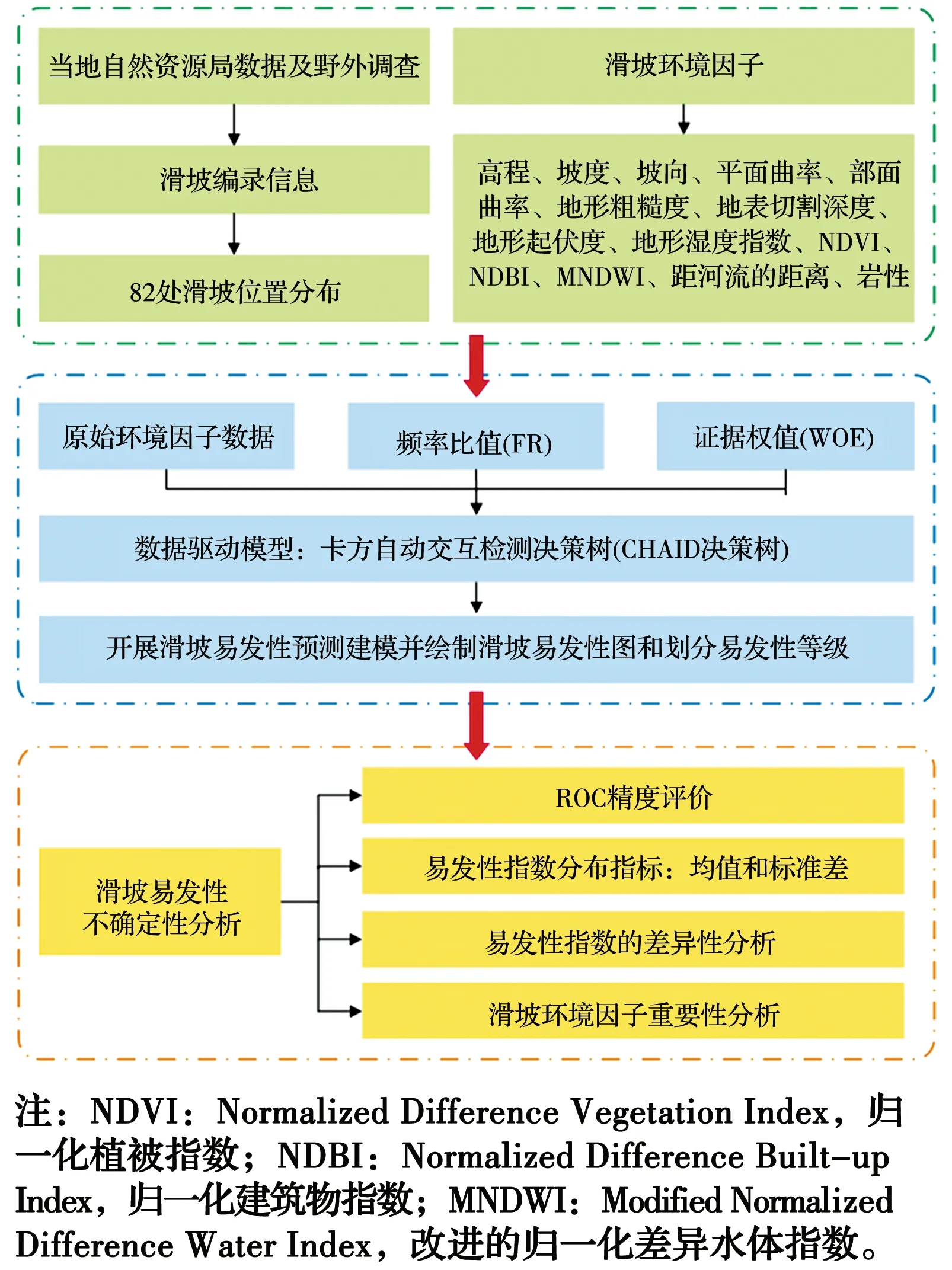
图1 滑坡易发性预测建模流程图Fig.1 Flowchart of landslide susceptibility prediction
1.1 滑坡与环境因子的关联分析法
1.1.1 频率比 频率比(Frequency Ratio,FR)反映了滑坡在各环境因子类别的分布状况,阐述环境因子各属性区间对滑坡的相对影响度,并且能够很好地解释滑坡与各因子之间的内在联系[25]。FR>1代表在对应的环境因子条件下利于滑坡事件的发生;FR<1表明该环境因子区间的属性与滑坡的发展关系较弱。利用环境因子的FR值作为各模型的输入变量之一,其计算公式如式(1)。
(1)
式中:Nj为环境因子某区间中出现的滑坡栅格数;N是全区已知滑坡所分布栅格的总数;Sj是环境因子的单元数;S是全区栅格总数。
1.1.2 证据权 证据权(Weight of Evidence,WOE)法在贝叶斯准则基础上综合各类证据层来实现定量计算某事件的发生概率。WOE法通过将滑坡编录和各类环境因子层进行空间关联,从而得到滑坡处各环境因子的详细分布特征权重因子W+和W-,其在每个环境因子分级中的计算如式(2)、式(3)所示。
(2)
(3)
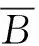
1.2 卡方自动交互检测决策树
CHAID决策树以卡方统计量为基础实现最优决策树构建,也就是通过自变量和因变量间的解释性来实现因变量的自动判别。CHAID决策树具有强大的非线性拟合预测性能,能容忍样本数据缺失及样本量不足等缺陷。CHAID模型设定树生长的层数、分裂及聚合阈值等停止标准来构建准确高效的预测或分类模型,同时,为防止过拟合现象而用随机分成的训练样本构建模型;最后再利用随机分成的测试样本对CHAID进行逐步检验,以修正模型参数。
1.3 不确定性分析方法
1.3.1 ROC 曲线精度分析 采用受试者工作特征(Receiver Operating Characteristic,ROC)曲线下面积(Area Under ROC,AUC)值作为一种量化指标来整体评估建模性能。ROC曲线对测试集中各样例进行排序并依序选择各截断点,再逐个把样例作为正例来进行计算,依据当前分类器的“真阳率”和“假阳率”进行ROC曲线的绘制,相关评价指标如表1所示。AUC值等于随机挑选的正样本的排名高于随机挑选的负样本的概率,AUC值越大,则易发性模型预测性能越好[4]。
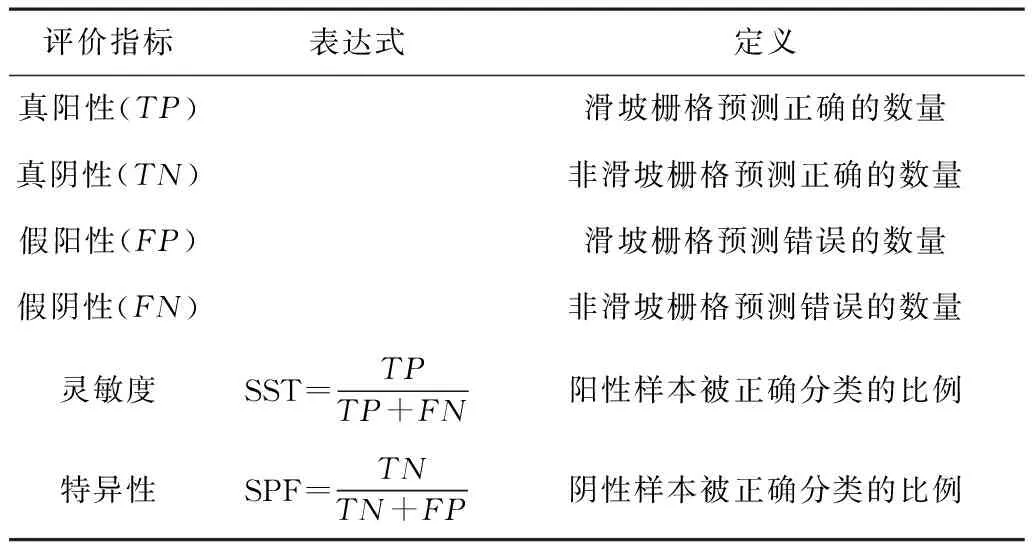
表1 ROC曲线的相关指标
1.3.2 易发性指数统计规律分析 均值(Mean)是集中趋势的测量,计算如式(4)所示(式中:Xn为第n个栅格单元的滑坡易发性指数值),其量化了研究区LSIs分布的整体偏向趋势,反映了LSIs分布的平均水平。标准差(Standard Deviation)是对围绕平均值的离差的测量,计算如式(5)所示(式中:μ为滑坡易发性指数均值;Xi为第i个栅格单元的滑坡易发性指数值),量化了LSIs分布的离散程度,标准差越小,说明LSIs越接近平均值,反之,则说明其与平均值的差异越大。采用均值和标准差从整体上分析LSIs的分布特征,揭示不同关联分析法和模型耦合模型下的预测性能,为滑坡易发性研究提供理论指导[23]。
(4)
(5)
1.3.3 易发性指数的差异显著性 采用显著性差异水平进一步分析各耦合模型下易发性建模的不确定性。具体采用Kendall协同系数检验法,对任意两组不同耦合模型下预测出的LSIs进行差异显著性检验。若Kendall秩相关系数W小于1及检验结果的显著性小于0.05,说明这两组耦合模型下LSIs的差异是显著的,拒绝原假设。本文通过成对因子显著性检验发现,W值为0.139,小于1,且P值均小于0.05,可见,各耦合模型下的LSIs间差异显著[27]。
2 延长县简介及环境因子分析
2.1 延长县简介及滑坡编录
延长县位于陕西东部,面积约2 368.7 km2,地势从西北向东南方向倾斜。县境内属黄土高原丘陵沟壑区(河谷阶地、黄土沟谷区、黄土沟间区和岩质丘陵区),出露三叠系中上统内陆湖相碎屑沉积岩和第四系风积、冲洪积和堆积黄土等地层,新近系砂砾岩在研究区出露较少(图2)。另外,县境内地质构造活动强度低,属于暖温带干旱大陆性季风气候,年均降雨量约564 mm且集中在7、8、9月份。
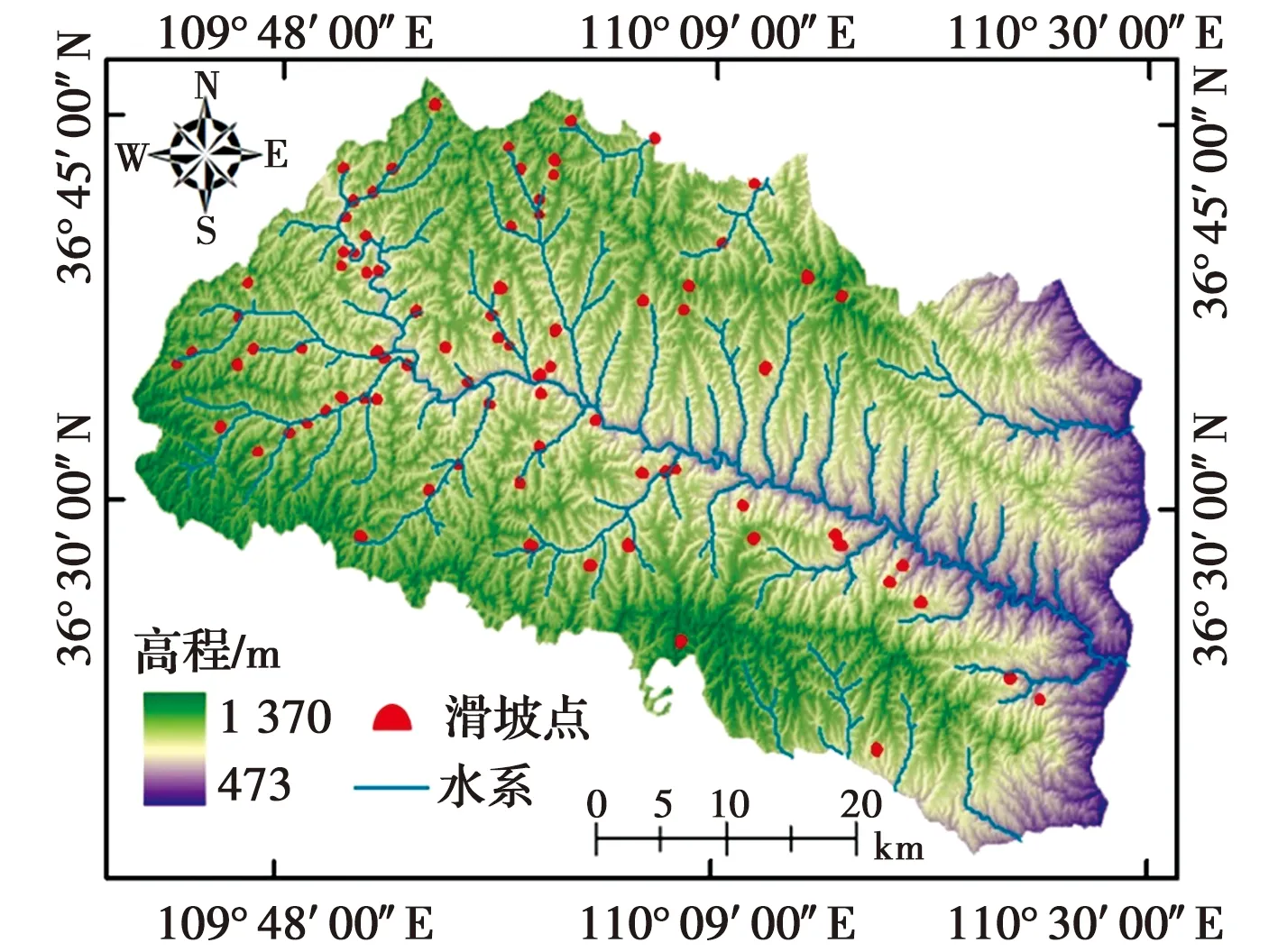
图2 延长县滑坡编录图Fig.2 Landslide inventory map of Yanchang
根据已有的滑坡野外调查资料和数据库可知,延长县共发生滑坡82处,主要类型为小型浅层覆盖滑坡,主要运动方式为牵引式(59%)和推移式滑动(41%);县境内的小型滑坡45处(占比54.8%),中型滑坡36处(占比43.9%),大型滑坡只有1处。延长县滑坡分布位置如图2所示,滑坡主要分布在县域西部及周边地区,东部和中部较少;大部分发生滑坡的位置地势较高,距离河流水系也较近。延长县滑坡的发生与地层岩性和工程活动密切相关。
2.2 环境因子分析
2.2.1 环境因子介绍 根据延长境内滑坡的特征及相关参考文献的介绍,利用遥感影像和GIS软件系统从数据源中提取14类滑坡环境因子,包括地形、水文、地表覆被和基础地质等[28-29]。其中,高程、NDVI、NDBI和MNDWI等12个因子为连续型数据,而距河流距离和地层岩性2个因子为离散型数据(表2)。对于连续型环境因子,先通过小间隔对该因子进行等分,再依据FR和WOE值将数值相近的区间合并成一个类别[30]。对于离散型数据类型的环境因子,采用固有的自然分组来进行分级:距河流距离因子按照距河流距离100、300、400、500、800、900、1 000 m和大于1 000 m进行分类;地层岩性因子为三叠系砂岩夹砂质泥岩和油页岩(T2t)、三叠系厚层砂岩夹泥岩(T3h)、三叠系细砂层粉砂岩夹与泥岩互层(T3y)、三叠系厚层状长石石英砂岩(T2w)和第四系更新统风积和洪积黄土(Qp1-3)[31]。另外,在使用原始因子数据作为CHAID决策树模型的输入变量时,将距河流的距离和地层岩性两种离散型数据类型的环境因子进行了“哑变量”处理。
2.2.2 地形地貌因子 高程、坡度、坡向、剖面曲率、平面曲率、地形起伏度、地形粗糙度、地形切割深度和地形湿度指数等环境因子均从DEM中提取(图3)[23,32]。以地形起伏度为例,分析其8个等级区间内的FR和WOE值(表2),发现滑坡发生概率与研究区的地形起伏度大小成正比。在20~4区间内发生滑坡的概率最大,为78.34%;其中,FR值均大于1,WOE值均为正值,35~40区域内FR和WOE值最大,分别为2.843和1.148。FR和WOE值都显示出地形起伏度大小与滑坡发生有着较强的正向相关性,可见关联分析法在表达滑坡与地形起伏度的非线性关联性时具有较为一致的趋势和计算效果。
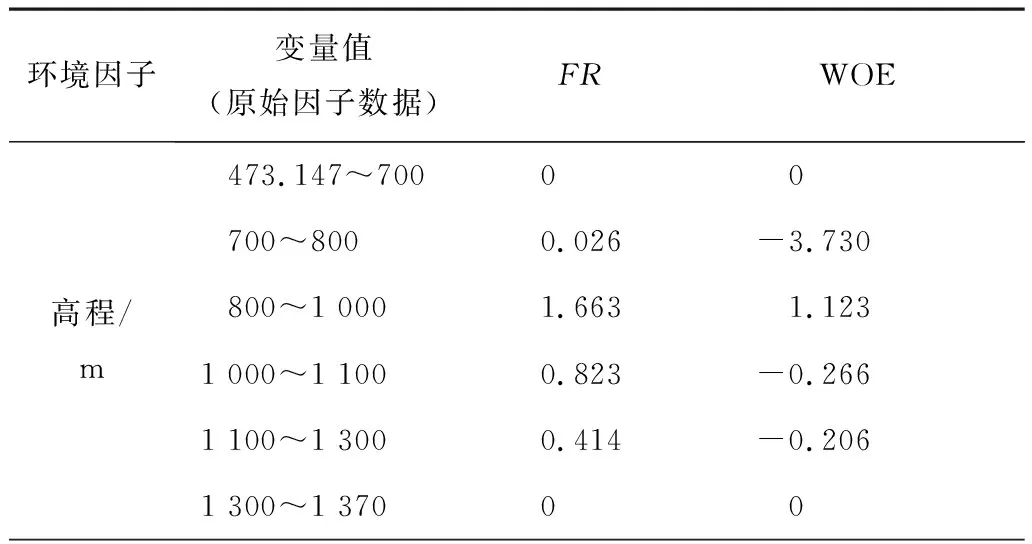
表2 环境因子的关联分析值
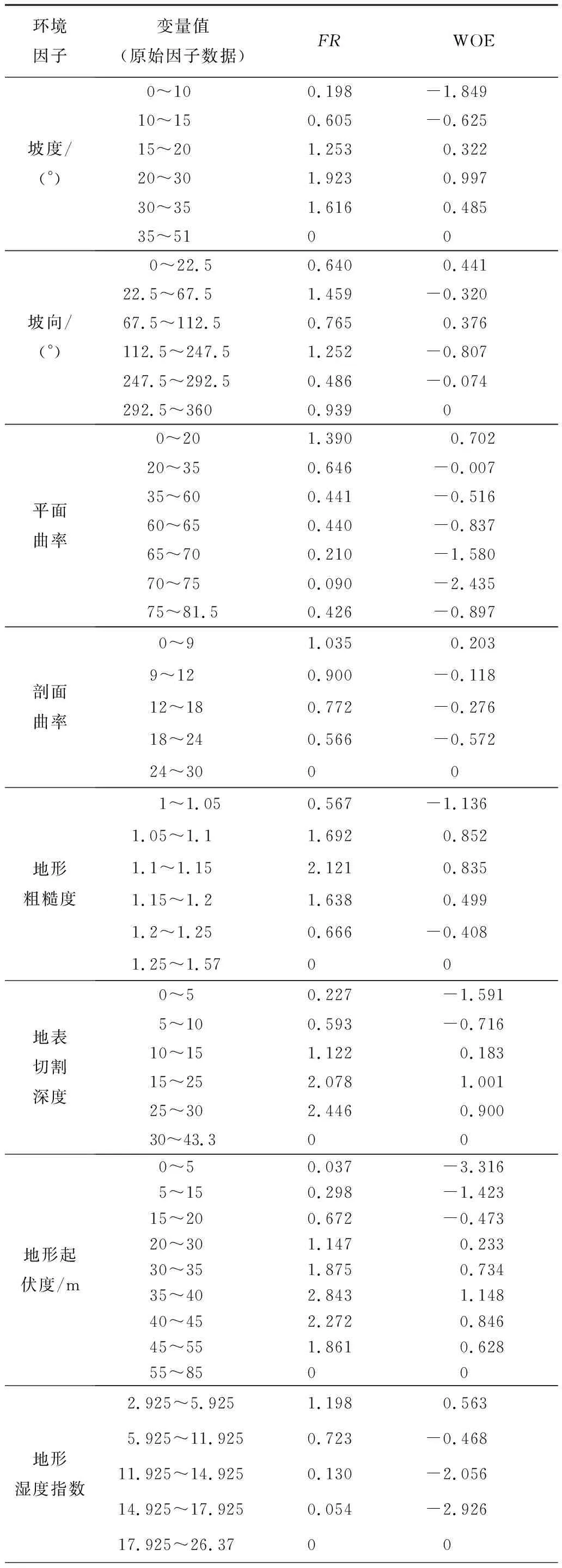
续表2
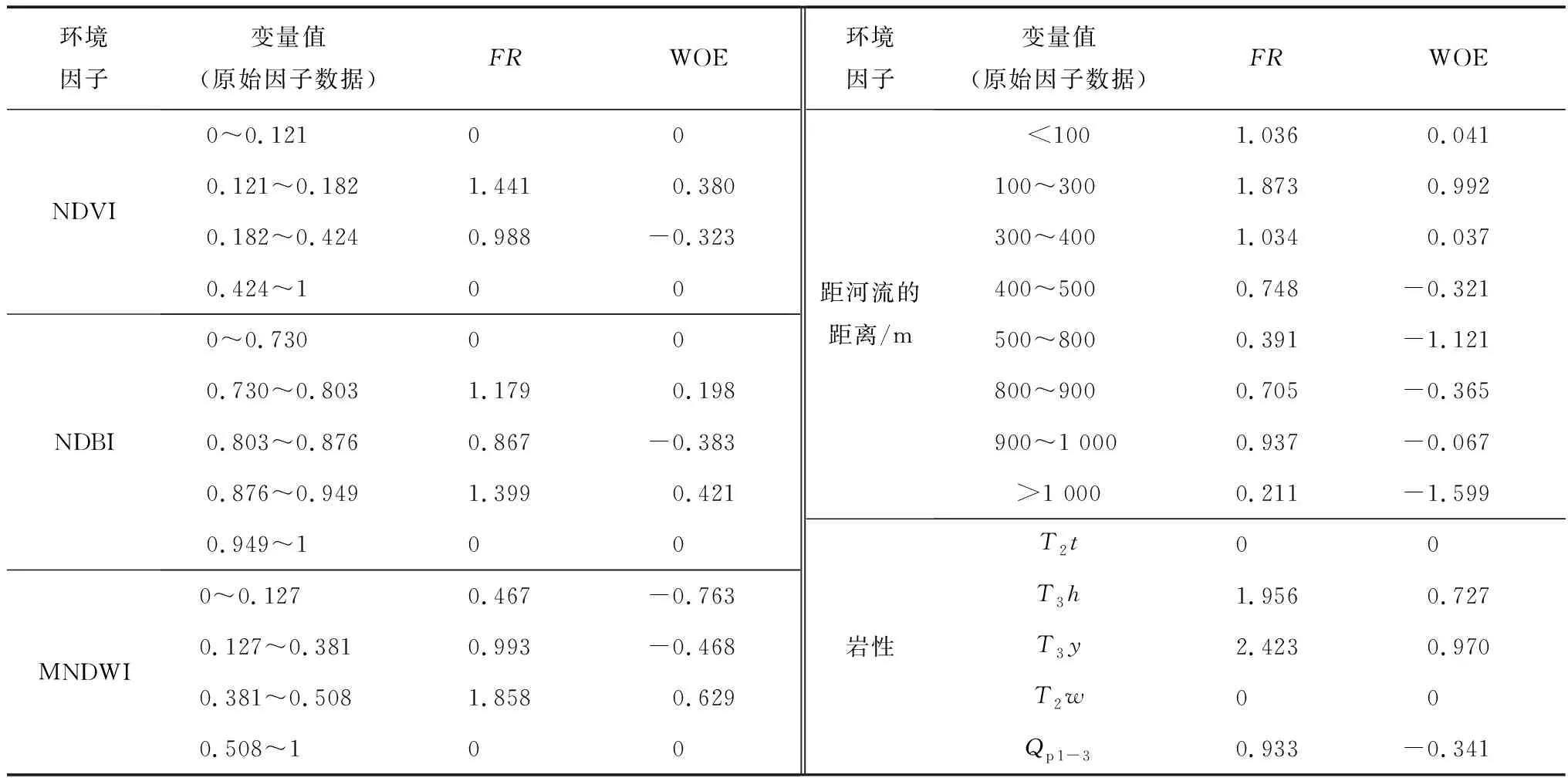
续表2
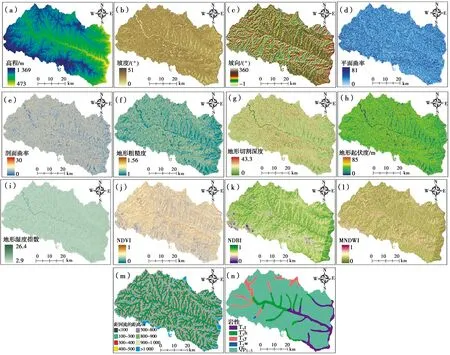
图3 延长县滑坡环境因子Fig.3 Landslide environmental factors in Yanchang
2.2.3 水文环境因子 由于河流对边坡的浸润和侵蚀作用,越靠近河流的边坡土壤含水量可能越高,导致斜坡体失稳的可能性更高[33-34]。利用距河流距离和MNDWI来表征水文环境对滑坡发育的影响。以距河流的距离因子为例(表2),当距河流距离小于400 m时,滑坡发育的可能性更高(达74.41%),其中,FR值均大于1,WOE值均为正值;在100~300 m区域内,FR和WOE值最大,分别为1.873和0.992。
2.2.4 地表覆被因子 NDBI和NDVI分别反映了研究区域内的建筑分布和自然植被对滑坡地质灾害发育的影响[35]。从表2可知,当NDVI在0.121~0.424范围内时,其与滑坡有较强的关系,该区间包括了研究区内近年来所有的已发生的滑坡;其中,在0.121~0.182范围内,FR值大于1且WOE值为正数。NDBI能较好地反映研究区域内建筑的分布情况,当NBVI在0.730~0.949范围内时几乎囊括了近年来研究区内所有的滑坡,间接反映了人类工程建设对滑坡发育的影响。
2.2.5 基础地质因子 岩土类型表征滑坡体的物质基础[36-37],分析表2可知,T3h和T3y岩性区域面积仅占延长县面积的10.6%,而区域内滑坡发生的概率高达23.2%,且FR值均大于1、WOE值均为正值,说明T3h和T3y岩性区域内滑坡发生的频率较高;在Qp1-3岩性条件下,滑坡发生概率高达76.8%;在T2t岩性区域内,无滑坡分布;T2w岩性区域在研究区内占比比较小,结果不具有研究意义。
3 延长县滑坡易发性预测建模
3.1 数据准备
30 m分辨率的栅格被广泛用作滑坡易发性的制图单元,基于30 m分辨率,整个延长县被划分为2 622 482个栅格,已发生的82处滑坡被划分为3 403个滑坡栅格[38]。通过FR和WOE两种关联法对14个环境因子各属性区间进行重新赋值,作为CHAID决策树开展易发性建模的输入变量;同时,也以原始因子数据作为输入变量开展单独CHAID决策树的滑坡易发性建模。通过SPSS modeler 18.0软件把3 403个滑坡栅格单元赋值为1,同时随机挑选与滑坡单元相同数量的非滑坡单元,并将其易发性赋值为0,作为模型输出变量;然后按7∶3随机划分滑坡和非滑坡栅格单元(6 806个)及其相关属性值,得到模型训练集和测试集。最后将整个研究区栅格单元的FR和WOE关联分析值以及原始因子数据代入训练好的模型中,预测延长县LSIs,并将其按照自然间断点法[39]划分为5个易发性级别。
3.2 延长滑坡易发性预测结果
在SPSS modeler软件中进行CHAID决策树建模。以WOE样本数据为例,首先需从外部源中读取源节点,将6 806个滑坡-非滑坡样本数据导入SPSS modeler软件中;接着对字段属性、测量级别及各字段在建模中的角色进行选择或修改;再经由分区选择将样本数据分为训练集(70%)和测试集(30%);然后在CHAID建模节点字段选项卡中使用预定义角色,应用boosting算法创建一个整体,由其生成模型序列以增强模型预测的准确度;选择CHAID树生长算法并定制树的最大深度值为5、父节点的最小记录数为75、子节点的最小记录数为15,以此来限制决策树的增长;CHAID决策树的其他参数使用SPSS modeler中的默认值;最后将整体环境因子的WOE带入训练好的CHAID决策树模型中,实现延长县滑坡LSIs的准确预测。FR-CHAID和单独CHAID决策树模型的建模步骤和参数设置与WOE-CHAID决策树模型基本一致。
3.3 滑坡易发性制图表达
分两步开展滑坡易发性制图,首先将3种耦合模型预测出的LSIs导入GIS软件中,然后依据自然间断点法将延长县滑坡易发性划分为极高、高、中等、低和极低5类等级区间[33]。WOE-CHAID、FR-CHAID和单独CHAID决策树模型下的滑坡易发性结果如图4所示。延长县大部分地区属于低和极低易发区,滑坡高和极高易发区主要位于坡度和高程中等且距离河流较近的山地丘陵地区。但3种耦合模型下得到的滑坡易发性级别存在显著差异,图4中延长县内已发生的82处滑坡几乎都落在WOE-CHAID和FR-CHAID决策树模型预测的极高与高易发性等级区域内,而单独CHAID决策树模型预测的极高与高易发性等级区域与82处滑坡位置存在些许偏差。
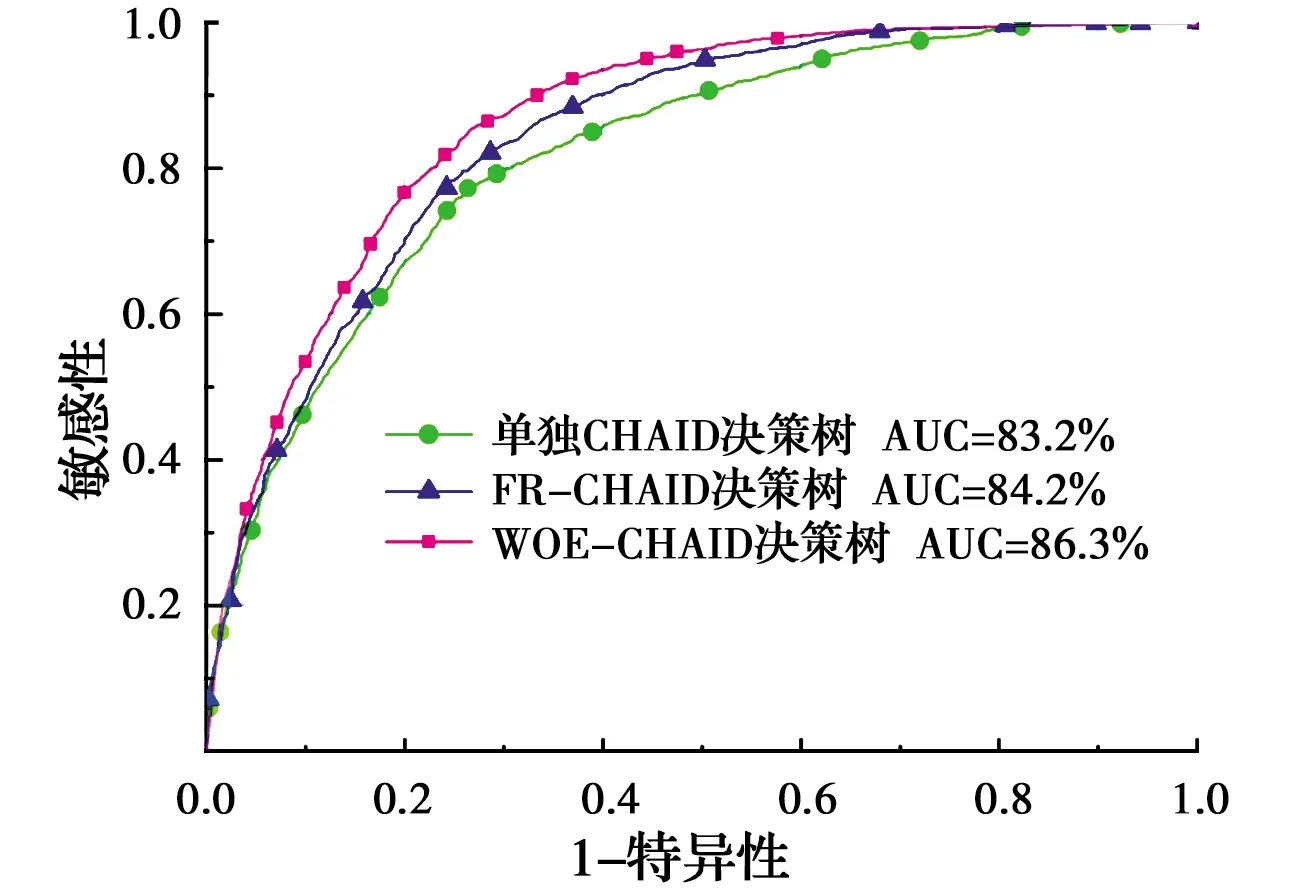
图5 CHAID决策树模型的滑坡易发性建模ROC曲线Fig.5 ROC curve of landslide susceptibility modeling of CHAID decision tree
4 滑坡易发性预测不确定性分析
4.1 ROC精度评价
采用测试集AUC值作为具体指标量化不同耦合模型的预测性能,AUC值越大,表明耦合模型预测性能越优。WOE-CHAID、FR-CHAID和单独CHAID决策树模型的滑坡易发性结果ROC曲线如图5所示。从图5中可知,3种耦合模型下的结果均较好且相对稳定,表现出良好的滑坡易发性性能。AUC精度从大到小依次为:AUC(WOE-CHAID)>AUC(FR-CHAID)>AUC(单独的CHAID),说明FR和WOE两种关联分析法在CHAID决策树模型中具有比原始因子数据更稳定的易发性预测性能。WOE耦合CHAID决策树模型的易发性预测效果最好且预测效率最高,AUC精度较FR提高了2.1%,较原始因子数据提高了3.1%。
4.2 滑坡易发性指数分布规律
采用均值和标准差分别反映LSIs分布的平均水平和离散程度,并以此分析耦合模型下的易发性预测不确定性。WOE-CHAID、FR-CHAID和单独CHAID决策树模型预测的LSIs分布不确定性规律较为一致,在极低和低易发区分布较集中而在高和极高易发区分布逐渐减少。LSIs平均值从小到大排名为:单独的CHAID (0.364) 图6 CHAID决策树模型的LSIs分布Fig.6 LSIs distribution of CHAID decision tree 采用显著性差异水平来进一步分析各耦合模型下易发性建模的不确定性,通过该试验计算各耦合模型下预测的LSIs的平均秩,以便对易发性模型性能排序。平均秩越小则模型性能越好,最终模型比较结果为:WOE-CHAID决策树模型预测LSIs的平均秩(值为1.85)最小,其次是FR-CHAID(值为2.06) 和单独的CHAID决策树(值为2.09)模型。显著性差异水平和平均秩显示出各耦合模型的易发性建模存在不确定性,如何规避这些不确定性是获得可靠的易发性模型的重要研究内容。 滑坡环境因子的重要性反映了已发生的滑坡事件受该环境因子影响程度的大小[40]。由于原始因子数据和不同的关联分析值在易发性预测建模中有着不同的表现,基于CHAID决策树模型中自带的分类器属性来评估在原始因子数据、FR和WOE等输入变量下各个环境因子的重要性。另外,易发性建模中共使用14个环境因子(原始因子数据含“哑变量”类型,共23个环境因子),排名10名之后的环境因子重要性均小于0.04,因此仅展示重要性排名前10的环境因子。从图7可知,坡度、地形起伏度、距河流的距离(原始因子数据中为100~300 m和500~800 m的两个“哑变量”因子)、地形切割深度和地形粗糙度等5个环境因子在单独CHAID、FR-CHAID和WOE-CHAID决策树易发性预测中有着较大的贡献,占据重要性排名均在前5位,重要性均大于0.08。其次,平面曲率和地形湿度指数在所有决策树模型中也发挥着相对重要的作用,重要性均大于0.04。 图7 滑坡环境因子重要性Fig.7 The importance of environmental factors of 关联分析法通过定量统计可直观表现各环境因子不同属性区间对滑坡易发性空间的影响性。Li等[27]、Saha等[41]对上述部分关联分析法反映滑坡与其环境因子空间关联的性能进行了对比分析,所得结果与笔者研究基本一致。由上述分析可知,环境因子与滑坡间的空间信息的关联性表达越充分,则LSIs的区分度越大,进一步的易发性预测效果就越佳。在FR和WOE关联分析法的环境因子分级中,WOE更能反映环境因子内部影响滑坡发育的空间信息的差异,具有更优的预测精度(AUC=86.3%);FR相较于WOE法更加简洁高效,在保证易发性精度的同时能有效避免太复杂的统计分析;基于原始因子数据进行的单独CHAID决策树模型易发性预测精度略小于FR-CHAID和WOE-CHAID决策树模型。此外,单独的CHAID、FR-CHAID和WOE-CHAID决策树模型预测的LSIs平均值逐渐减小而标准差逐渐增大,且平均秩也逐渐减小。可见关联分析法的易发性预测建模效果较好,WOE优于FR,而原始因子数据的易发性建模效果较差。 由文献[27,42]可知,滑坡与环境因子(不考虑诱发因子)之间的非线性关联分析法种类繁多。笔者仅使用FR和WOE两种关联分析法耦合CHAID决策树模型进行滑坡易发性的不确定性对比分析而并未考虑其他关联分析法,在下一步研究中可以考虑使用概率法、信息量、确定性系数和熵指数等其他关联分析法,耦合多种不同类型的模型开展更加全面的易发性预测不确定性分析。 1)WOE-CHAID决策树模型易发性预测的AUC精度最高,且均值和平均秩较小,标准差较大;FR-CHAID决策树的AUC精度略低于WOE-CHAID,可见WOE具有更优秀的非线性关联性能。 2)将原始因子直接用作输入变量的单独CHAID决策树模型的易发性预测精度整体略低于关联分析法的耦合模型。为了提高滑坡易发性建模效率,可直接使用单独CHAID决策树模型,但要体现滑坡与其环境因子的空间关联性或分析环境因子各子区间对滑坡发育的影响规律,则使用关联分析法和CHAID决策树模型耦合建模的优势显著。 3)总体来说,WOE-CHAID决策树模型的易发性预测结果可靠性最高,预测出的LSIs与实际的滑坡概率分布特征更加相符。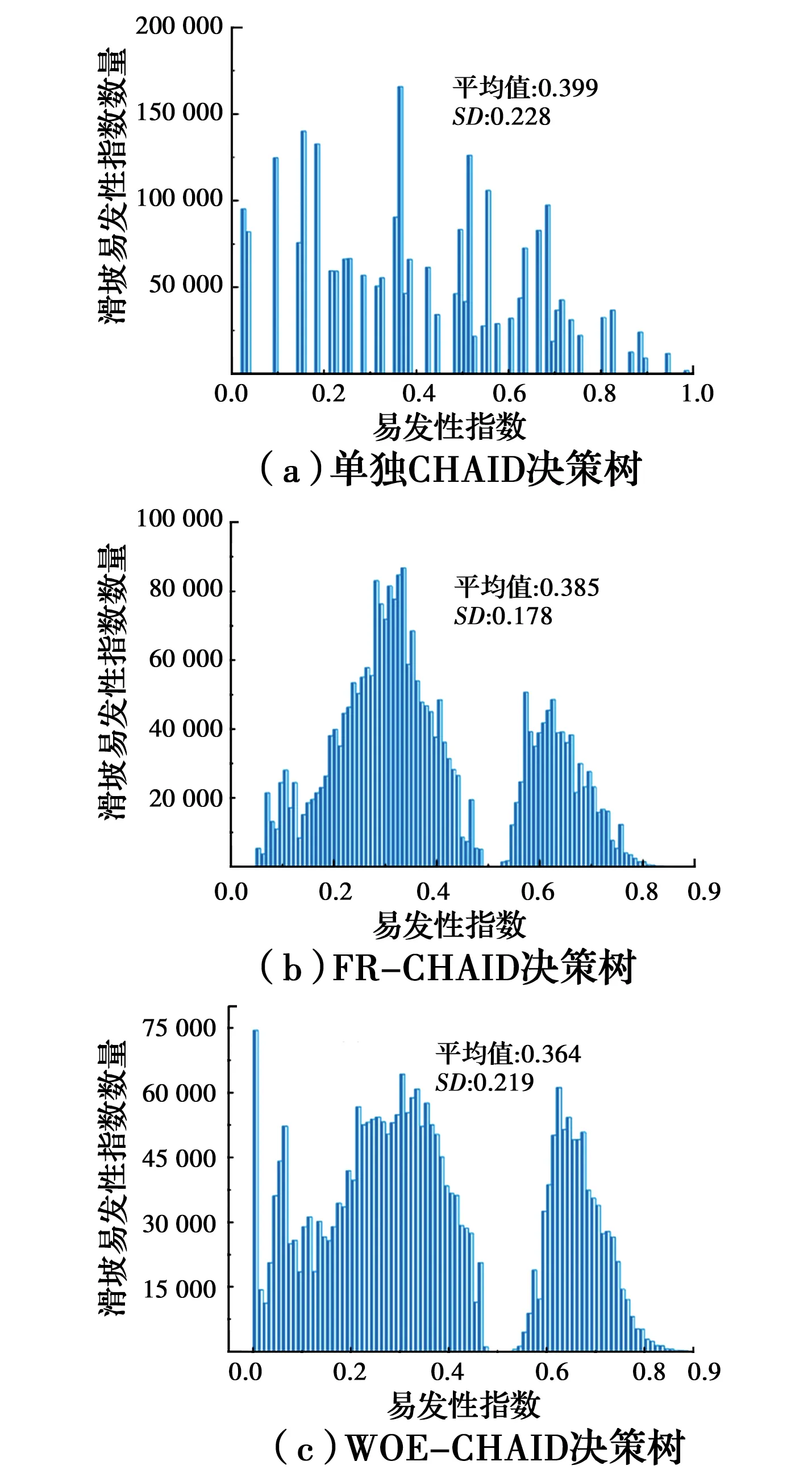
4.3 耦合模型预测易发性指数的差异性分析
4.4 滑坡环境因子重要性分析
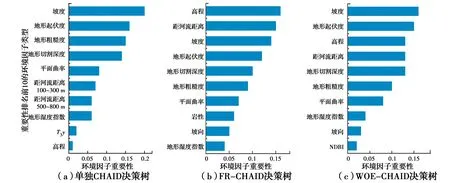
4.5 各关联分析法的性能分析
5 结论

