边坡支挡结构岩土荷载的分项系数计算方法

王桂林，陈瑶，杨洋

(重庆大学 a. 土木工程学院；b. 库区环境地质灾害防治国家地方联合工程研究中心(重庆)； c. 山地城镇建设与新技术教育部重点实验室，重庆 400045)

目前，边坡(滑坡)支挡结构岩土荷载常采用单一安全系数法来确定[1-2]，但安全系数受工程经验影响较大，不能充分反映支挡结构设计的岩土参数变异性与安全裕度[3-5]。因此，学者们对边坡支挡结构岩土荷载计算进行了深入研究。

方玉树[6]分析了支挡结构岩土荷载取值方法，认为应根据稳定性进行计算，并指出支挡结构岩土荷载既不是滑坡推力也不是主动土压力。付文光等[7]指出相关标准中稳定安全系数计算公式存在着5类抗力与荷载错位、不符合安全系数定义的现象，导致有时工程安全储备不足或较大浪费。Wu等[8]首次提出利用可靠度理论评价边坡稳定性，此后，利用可靠度理论求解边坡支挡结构岩土荷载的方法逐渐发展。祝玉学[9]对可靠度用于边坡工程做了专门的解释；唐小松等[10]基于Copula理论研究了有限信息情况下的边坡可靠度研究方法；周泽华[11]系统研究了抗剪强度参数的联合分布与边坡可靠度的关系。但可靠度方法计算繁琐复杂，未能在实际工程中得到推广使用。分项系数极限状态设计方法是一种与规定目标可靠度相联系的设计方法，通过各变量的分项系数反映其变异水平，使结构功能函数通过显示方式表达，提高了准确度，广泛应用于桥梁、水利、灾害防护等多个结构工程领域的安全性研究[12-14]。在边坡工程方面，陈祖煜[15]根据安全系数与可靠指标提出了相对安全率的概念，并研究其作为安全判据在重力坝边坡等工程中的适用性。黎康平[16]通过对比基于可靠度的安全系数标准和分项系数标准，研究了重力墙及土石坝的稳定性。李昂等[17]研究了几何和强度参数对分项系数的影响规律，提出了对应小、中、大3种变异水平的分项系数推荐值。但现有边坡工程设计对分项系数法的应用与规定还较为简单，有待进一步研究。

为了进一步探索分项系数法在边坡支挡结构设计方面的适用性，笔者采用一般分离法推导出边坡的分项系数以及荷载值的计算公式，将抗剪强度参数黏聚力c和摩擦系数f视为随机变量，通过算例比较分项系数法与蒙特卡罗法在单一型滑面和折线型滑面边坡可靠度的偏差，并分析其原因。

1 分项系数法

分项系数γ通常为变量的设计值与标准值的比值。一般情况下，影响边坡稳定性的因素分为边坡的抗滑力R与边坡的下滑力S，描述边坡稳定性的函数定义为其功能函数Z，表示为Z=g(R,S)=R-S。现将支挡结构岩土荷载R0加入到功能函数，得到边坡的功能函数在极限状态下的表达式，见式(1)，示意图见图1。

Z=R+R0-S=0

(1)

式中：R0为支挡力，kN，其方向与所在条块滑面倾向相同；S为边坡下滑力；R为边坡抗滑力，计算公式见式(2)、式(3)。

(2)

(3)

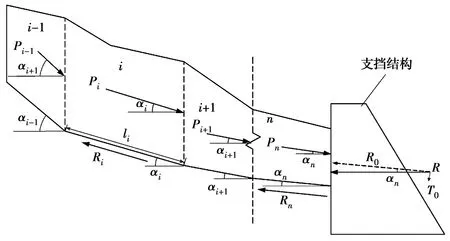
图1 边坡滑块及支挡结构受力示意图Fig.1 Force diagram of slope block and supporting

图1中，Pi为第i滑块的剩余下滑力，为该滑块的下滑力与抗滑力差值；R为支挡结构对最底部滑块的总支挡力；R0和T0分别为沿着底部滑块倾向和垂直底部滑块倾向的支挡分量。

根据一般分离法思想，可对任意变量Xi、Xj进行式(4)所示的公式变换。

(4)

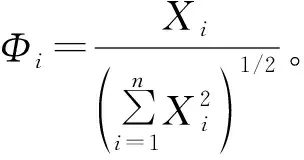
对抗剪参数c、φ的分项系数γc和γf进行求解。假定下滑力S和抗滑力R均服从正态分布，根据一般分离法及可靠度指标的表达式，可得式(5)。

βΦRσR+βΦSσS

(5)

式中：μR为抗滑力均值；μS为下滑力均值；β为可靠度；σR为抗滑力标准差；σS为下滑力标准差；ΦR、ΦS为分离函数，表达式分别见式(6)、式(7)。

(6)

(7)

将式(2)和式(3)代入式(5)，可得式(8)。

(8)

根据变异系数的定义，抗剪参数均值与标准差存在关系

σc=δcμc,σf=δfμf

式中：δc、δf分别为黏聚力和摩擦系数的变异系数，将其代入式(8)，可得式(9)。

(9)

移项整理后得到边坡支挡结构岩土荷载的计算式，见式(10)。

(10)

式中：γc为黏聚力的分项系数，γc=1-βΦcδc，当γc<0时，取γc=0；γf为摩擦系数的分项系数，γf=1-βΦfδf，当γf<0时，取γf=0；Φc、Φf分别为黏聚力和摩擦系数的分离函数，表达式见式(11)、式(12)。

(11)

(12)

2 与目标可靠度指标印证及讨论

由于分项系数可以反映支挡设计后边坡需要达到的可靠度指标，因此，按分项系数法计算所得到的荷载进行边坡支护，支护后边坡的可靠度指标理论上应等于计算时设定的目标可靠度指标，即分项系数设定的目标可靠度与实际可靠度之间存在相互印证，印证的流程如图2所示。

图2 相互印证流程图Fig.2 Flow chart of mutual

印证时，边坡实际可靠度采用蒙特卡罗法计算，通过输入黏聚力与摩擦系数的分布区间以及分项系数法得到的支挡荷载，计算判断边坡是否失稳破坏，取重复次数N=5 000，得到失稳破坏次数与N的比值即为失效概率，进而得到可靠度β。

选取单一滑面和折线型滑面两类典型滑面的边坡案例进行计算印证。根据概率统计知识，当功能函数服从正态分布时，失效概率Pf与可靠度指标β的关系见表1。

表1 失效概率与可靠度指标大小关系

2.1 算例一

取单一滑面的边坡模型，上部为土层，下部为岩体，边坡几何参数有上覆土层厚度H，滑面倾角α，如图3所示。模型参数取值分别为H=5 m、α=45°，土体重度γ=18 kN/m3。抗剪强度参数黏聚力c和摩擦系数f为随机变量，其统计特征见表2。

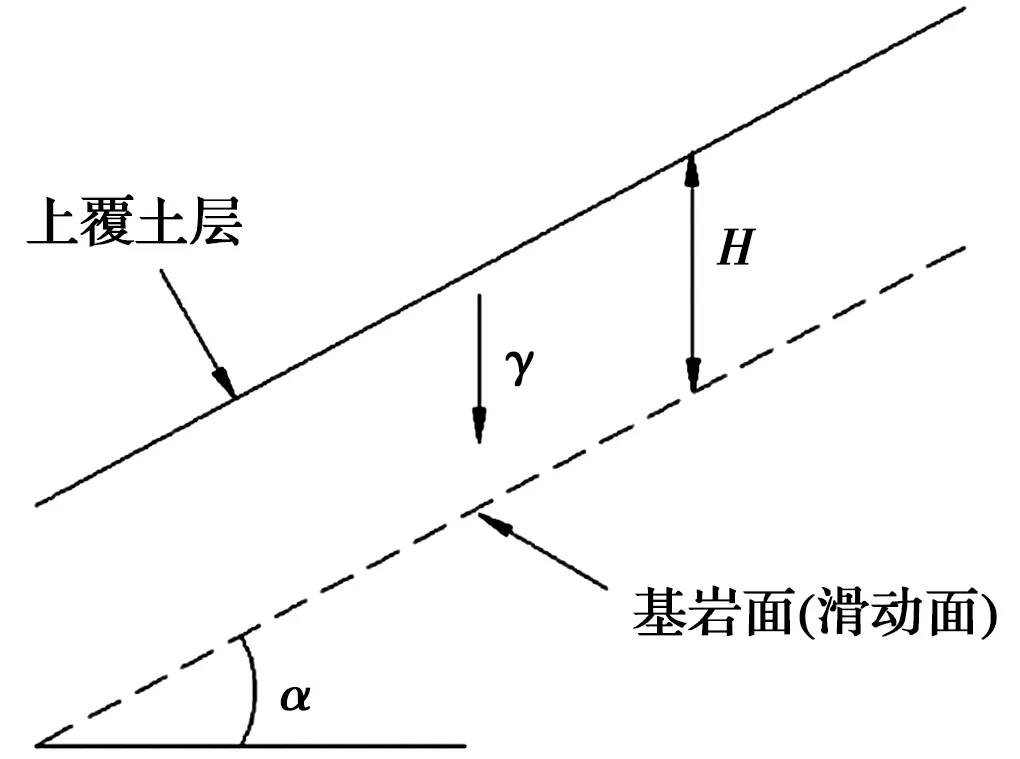
图3 算例1边坡计算模型Fig.3 Slope model of example

表2 黏聚力和摩擦系数的统计特征

2.1.1 边坡支挡结构岩土荷载计算 分离函数只与抗剪强度参数标准差有关，与目标可靠度指标无关，根据式(11)和式(12)计算分离函数。

黏聚力的分离函数

摩擦系数的分离函数

按照式(10)进行支挡结构岩土荷载的计算。不同目标可靠度指标情况下，分项系数及支挡结构岩土荷载见表3。

表3 不同目标可靠度指标下支挡结构岩土荷载

2.1.2 支挡后可靠度与目标可靠度对比 根据表3的边坡支挡结构岩土荷载对边坡进行支挡设计，应用蒙特卡罗法求得支挡后边坡的可靠度指标β，并与分项系数法目标可靠度βT进行比较，结果见表4。

表4 目标可靠度指标与支挡后边坡可靠度指标对比

表4给出了目标可靠度指标βT和对应的支挡后边坡可靠度指标β以及二者之间的相对误差。支挡后边坡可靠度指标β与目标可靠度指标βT相对误差绝对值在0.9%～5.8%之间，其原因有：1)可靠度指标的计算方法不同，分项系数法计算过程是线性运算，而蒙特卡罗法的可靠度是由概率计算获得；2)抗剪强度参数变异性处理方式不同，分项系数法只考虑了抗剪强度参数概率上的变异性，而蒙特卡罗法采用随机场理论，考虑了抗剪强度参数的空间变异性。

2.2 算例二

某实际折线型滑面边坡上部主要为次生红黏土，少量碎石土和素填土，下面为岩体，滑动面为土岩分界面。边坡剖面高约420 m，长约120 m，土体重度γ=18 kN/m3，黏聚力c和内摩擦角φ视为随机变量，统计特征见表5，边坡的计算剖面见图4，本算例不考虑地下水作用。

根据式(11)和式(12)，得到黏聚力的分离函数Φc=0.306 2；摩擦系数的分离函数Φf=0.952 0。

图4 计算剖面图Fig.4 Calculation sectional

表5 黏聚力和摩擦系数的统计特征

2.2.1 边坡支挡结构岩土荷载计算 分别取目标可靠度指标进行支挡结构岩土荷载的计算，在不同目标可靠度指标情况下，其分项系数及支挡结构岩土荷载见表6。

表6 不同目标可靠度指标下支挡结构岩土荷载

由表6可以看出，随着目标可靠度指标βT取值的增加，支挡结构岩土荷载大幅度增加，需要支护。目标可靠度指标βT的选取对支挡结构的设计有重要影响。

2.2.2 支挡后可靠度与目标可靠度对比及讨论 根据表6得到的支挡结构岩土荷载对边坡进行支挡设计，应用蒙特卡罗法求得支挡后边坡的可靠度指标β，并与分项系数法目标可靠度βT进行比较，结果见表7。

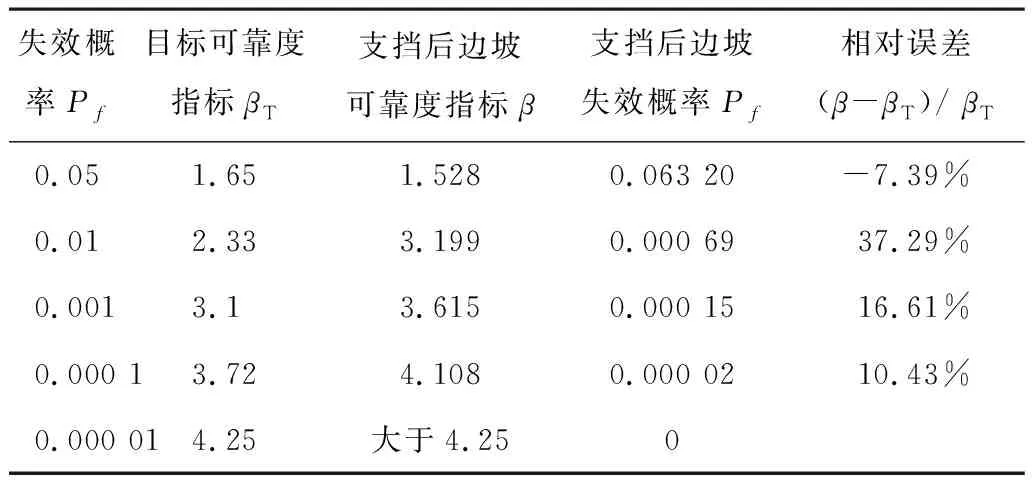
表7 目标可靠度指标与支挡后边坡可靠度指标对比

表7给出了目标可靠度指标βT和对应的支挡后边坡可靠度指标β，以及二者之间的相对误差。可以看出，相比算例1，算例2中目标可靠度βT和支挡后边坡可靠度指标β相差较大，当目标可靠度βT为1.65时，存在负偏差-7.39%，当目标可靠度βT大于1.65时则为正偏差，可见总体上是安全可控的。

βT和β产生误差的原因：除可靠度指标计算方法和抗剪强度参数变异性处理方式不同外，与计算过程结构功能函数是显式表达式Z=R+R0-S且忽略了条块间力传递的假定有关；除此之外，假定抗剪强度参数服从正态分布，未考虑各参数之间的关联性，然而，实际工程中岩土体参数分布类型的拟合并不都是正态分布，且各参数之间存在一定的关联性。

后续研究可从以上几个方面改进分项系数计算方法，并通过大量实例对相互印证过程进行对比分析，通过对比结果确定其相互印证程度，并采取有效措施改进分项系数计算方法和分项系数极限状态设计方法。

3 结论

采用一般分离法推导了边坡支挡结构岩土荷载分项系数表达式，并经算例进行了目标可靠度与实际可靠度的对比。结果表明：

1)通过分项系数法能方便地获得不同边坡目标可靠度指标值对应的支挡结构岩土荷载值。

2)在指定目标可靠度指标值时，单一滑面边坡的可靠度主要出现负偏差，偏差绝对值最大约6%；对于折线型滑面边坡，当目标可靠度指标为1.65时，是负偏差，偏差约7%，但目标可靠度指标大于1.65时，出现正偏差，总体上是安全可控的。

3)导致偏差的主要原因有：分项系数法与可靠度法可靠度指标的具体计算方法不同；抗剪强度参数变异性处理方式不同；结构功能函数忽略了条块间力；岩土体参数分布类型仅假定为正态分布且参数之间无关联。

4)单一滑面和折线型滑面边坡可靠度分析中，目标可靠度与支挡后边坡可靠度相对大小并不是固定的，即便如此，由于分项系数法可以考虑工程的安全裕度，计算简单，符合工程设计习惯，在工程中具有应用价值。