四元数神经网络的固定时间同步分析

王增赟，宋嗣琪

(湖南第一师范学院 数学与统计学院，湖南 长沙 410205)

1 研究现状

计算机神经网络通过模拟人脑神经网络的结构和功能进行信息处理，它具有很强的数据处理、联想记忆功能和适应能力。在过去的几十年里，相继有学者提出了不同的神经网络模型[1-5]。Isokawa等[5]首次提出了四元数神经网络模型(QNN)。四元数神经网络在图像处理、色彩融合和联想记忆等领域有独特的优势[6-8]。近年来，四元数神经网络大部分研究成果都集中在平衡点和周期解的存在性及稳定性上[9-11]。文献[9]详细介绍了线性时标四元数微分方程的基本理论，包括解的存在性和稳定性。文献[11]研究了四元数细胞神经网络周期解的存在性和指数稳定性。

自1990年Pecora和Carroll提出驱动—响应同步概念以来，渐进/指数同步和有限/固定时间同步成为过去十几年的热门研究课题[12-14]。固定时间同步能够刻画两个系统在任意初始误差的情形下达到完全相同的状态，因此研究神经网络的固定时间同步具有重要的意义。近年来，研究四元数神经网络的有限/固定时间同步的成果陆续出现[15-16]。文献[15]研究了四元数神经网络的固定时间同步，并设计鲁棒反馈控制器实现了网络的固定时间同步。文献[16]介绍了忆阻四元数神经网络模型，并设计了控制器来实现网络的固定时间同步。然而，已有的成果都依赖于传统的固定时间稳定性定理。

本文提出一个新的固定时间收敛定理，并给出严格的数学证明。随后，基于该定理，分析了四元数神经网络的固定时间同步。

2 四元数神经网络模型与预备知识

2.1 四元数神经网络模型

四元数神经网络模型的主系统为：

(1)

式(1)的向量形式为：

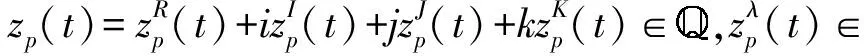
接下来考虑四元数神经网络模型的从系统为：

(2)

定义误差系统为：

ep(t)=sp(t)-zp(t)。

(3)

利用Hamilton法则将误差系统的实部和虚部分离，可得

(4)

2.2 预备知识

在进一步分析四元数神经网络的固定时间同步之前，定义参数如下：

(5)

接下来，笔者给出固定时间同步的定义和一个有用的引理。

定义2.1 对任意的初始条件，存在不依赖于系统初值的时间变量，误差向量满足

引理2.1[17]如果x1，x2，…，xn≥0，0<ξ≤1，η>1，那么下面的不等式成立

3 固定时间收敛定理

下面介绍一个新的固定时间收敛定理。

(1)V(e(t))=0⟺e(t)=0，

(2)对于误差系统的每个解，存在α，β，M>0，0<ξ<1和η>1，满足

则误差系统的零解可以实现固定时间吸引性。此外，设定时间的估计为：

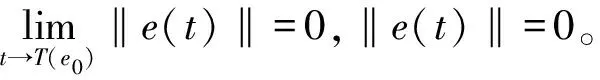
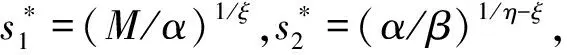
(1)如果0<(M/α)1/ξ≤(α/β)1/η-ξ≤V(e(0))，对∀s1，s2∈(0，V(e(0)))，可以得到

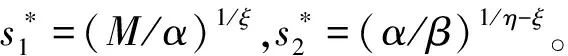
(2)如果0<(M/α)1/ξ≤V(e(0))≤(α/β)1/η-ξ，则

(4)如果0<(α/β)1/η-ξ≤(M/α)1/ξ≤V(e(0))，则

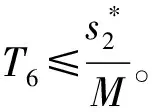
综合(1)—(6)可得

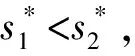
注3.2 从证明过程可以看出，当M=0时，定理3.1也不能退化成传统定理[18]。因此，本文的固定时间定理是一个新的固定时间定理。

4 固定时间同步分析

为了使系统(2)固定时间同步于系统(1)，设计下面的非线性控制器：

(6)

其中，p=1，2，…，n；δip是不确定的常数；σip，ρip，τip是正数，且0<ξ<1，η>1。

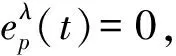
定理4.1 如果假设2.1成立，选择合适的参数满足下列条件：

δip≥ωip，i=1，2，3，4；p=1，2，…，n。

则系统(1)和系统(2)在控制器的作用下可以实现固定时间同步。此外，

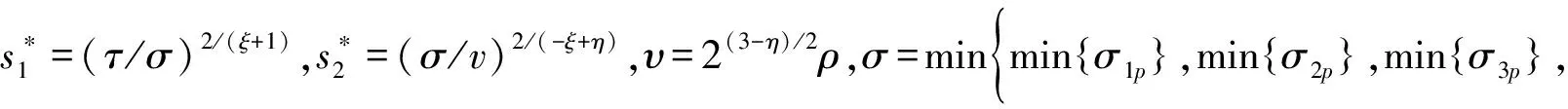
下面证明在控制器的作用下，系统(1)和系统(2)可以实现固定时间同步。

证明：构造一个李雅普诺夫(Lyapunov)函数：

对V1(t)求导，由系统(4)可得

由基本不等式可得

(7)

由假设2.1和式(2)，可得

(8)

又

(9)

由式(7)、式(8)、式(9)可得

(10)

同理可得

(11)

由式(10)、求(11)和参数(5)可得

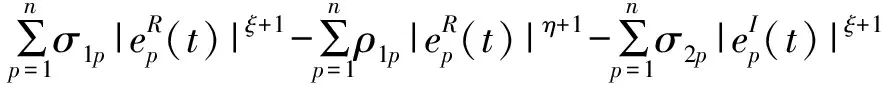
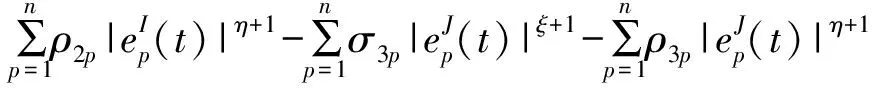
令

又0<(ξ+1)/2<1，(η+1)/2>1，若δip满足定理4.1的条件，由引理2.1可得

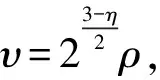
由定义2.1和定理3.1，在控制器的作用下，系统(2)的固定时间同步于系统(1)。同步时间的上界为：

所以定理4.1得证。

5 数值模拟

下面用数值模拟的方法来验证上述结论的正确性。

例考虑如下四元数神经网络模型作为主系统：

(12)

接下来考虑从系统为：

(13)

定义误差系统为ep(t)=sp(t)-zp(t)。

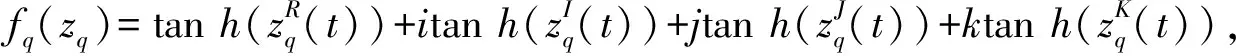
s1(0)=-3-1.2i+j-2.5k，s2(0)=2.1+0.5i-1.2j+0.3k。此外，其他参数为：

图1 状态变量zR1(t),sR1(t),zI1(t),sI1(t)在无控制器下的轨迹图2 状态变量zJ1(t),sJ1(t),zK1(t),sK1(t)在无控制器下的轨迹图3 状态变量zR2(t),sR2(t),zI2(t),sI2(t)在无控制器下的轨迹图4 状态变量zJ2(t),sJ2(t),zK2(t),sK2(t)在无控制器下的轨迹图5 误差变量eR1(t),eI1(t),eJ1(t),eK1(t)在控制器下的轨迹图6 误差变量eR2(t),eI2(t),eJ2(t),eK2(t)在控制器下的轨迹

根据定理3.1，主从系统达到同步的时间上限Tmax≈1.66 s。由图5、图6可知，主从系统在固定时间内可以达到同步。

6 结论

本文提出了一个新的固定时间收敛定理，并给出了时间上限，最后通过数值模拟证明了结论的有效性。由于固定时间同步与初始值无关，所以本文提出的新定理具有更强的实用性。