重点海域救助船布置位置的选择
李成海,俞启军,文 峰
(1.山东交通职业学院 航海系,山东 潍坊 261206; 2.自然资源部第一海洋研究所,山东 青岛 266011;3.东营港引航站,山东 东营 257000)
0 引言
为了提高海难船舶救助的成功率,各国救助站采用科学布置救助船选址的策略,为船舶海上航行保驾护航。但是,由于海区广阔以及救助船数量有限,往往存在救助效率低和救助不及时等问题。为了改变这一状况,救助专家提出了在重点海域科学布置救助船的理念和最大效率地利用现有救助力量的救助策略。在传统的理念中,需要大量的救助船对海区洋面进行全方位覆盖,这对大多数国家的海难救助来说是不现实的,因此如何使现有救助站的救助力量实现效率最大化是遇险船救助决策中亟待解决的问题。
现有关于海难救助的研究主要集中在宏观救助策略上。林婉妮等[1]根据巡逻船密度数据确定救援船舶的概率分布,分别计算风向影响下东海特定水域的海上救助效率。朱小林等[2]研究了海上应急救援系统中应急资源位置—分配决策问题,建立了基于事件类型的应急物资与船舶分配多目标模型,确定不同目标分量权重下合理的船舶、物资分配方法。郭国平等[3]利用P-中位建立了应急救助站点选址的数学模型,目标函数在满足设置的约束条件下取最小值(即救援用时最少或救援距离最短)。吴晓林等[4]建立救助船模糊相似优选模型,根据各指标的优选结果对所有待选船舶方案进行综合排序,选择最合适的救助船参与救助行动。李洪成等[5]以系统的时效性、安全性和经济性作为优化目标,建立多目标规划模型,并给出了模型的求解方法。黄敏东[6]通过对海上救援时间进行分析,论述海上黄金救援时间以及科学制定搜救措施等对提高海上救助成功率的影响。杨卫东[7]基于GIS并结合贪心算法,提出了连续设施选址问题的求解方案。
已有的研究成果为救助船救助的布置位置奠定了基础。但与以往的设施布置方案相比较,救助船的布置位置具有特殊性。所以,针对海上救助重点水域的覆盖问题,亟须在模型的构建和计算方法上进行改进。
1 救助问题
1.1 救助问题的分析
救助船的布置位置问题实际上是救助船停泊位置选址的问题。为提高救助成功率,应将救助船布置在最佳的救助位置。但是,由于救助船的数量有限,不可能全海域覆盖,所以只能有针对性地在重点海域安排现有的救助力量,从而实现切实可行的区域救助方案。研究的思路为:提出假想模型、精确构建模型、确定救助船位置选址,对影响救助结果的因素进行定性分析。
根据已有的研究成果确认影响救助结果的因素有以下4个。
(1)船速。船舶的类型不同航速也不同。以集装箱船为例,如果集装箱船大小不一、配置不同,则航行速度亦有较大差别。接到警报后,若对遇险船的位置信息掌握不全,会导致在整个海域投放救助船的位置出现偏差,延误救助时间。
(2)航线。如果遇险船是货轮,虽然其航线比较固定,但是航区范围很大。由于货轮航线的变化会导致救援时间不同,也会影响救助船的位置布置[8]。
(3)求助时间。遇险船发出求救信息的时间不同,留给救助船的救助时间也会发生很大变化。越早求救,救助船就越早采取救助行动,遇险船的损失就越少。
(4)遇险船的数量。若遇险船有多艘,且都出现在同一救助船的救助海域内,显然,一艘救助船无法兼顾多艘遇险船,故而,救助成功率会很低。但是,由于船舶集中发生海难的可能性不大,所以在模型中假设该情况不发生。
1.2 模型假设及参数
根据对影响遇险船救助因素定性分析的结果,在建模时有以下假设:
(1)遇险船类型相同,救助船吨位也相同,船舶间的差异主要体现在船速上[9]。
(2)所有船舶均匀速航速。
(3)救助船的救援目的地为预计遇险船与救助船相遇地点(即根据遇险船航行路径估算出的救助位置),并非遇险船的实时位置。
(4)只有当遇险船进入搜救指挥中心搜寻范围内才可能被发现,并通知最近的救助船开始施救[10]。
(5)一艘遇险船至少需要一艘救助船救助,即一艘救助船不能同时给多艘遇险船提供救助。
根据上述假设,使用数学语言对救助行动进行描述。
设:在航区航行的船舶有m艘,记为B=(b1,b2,b3,…,bm),遇险船为f艘,记为A=(a1,a2,a3,…,af),救助站有救助船t艘,记为D=(d1,d2,d3,…,dt)。
基础参数:



Ra为遇险船的航行半径,n mile;
Rd为救助船的航行半径,n mile;
T为以遇险船遇险时刻为起始时间,救助船开始向遇险船位置方向航行所需的准备时间;
Tji为从第i艘遇险船驶入第j艘搜救船舶搜救范围始计,至被第j艘搜救船发现并确认遇险船所消耗的时间;
Tjh为从第h艘救助船接到第j艘搜救船的求助信息始计,至第h艘救助船抵达遇险船位置所消耗的时间;



2 构建模型
依据救助程序,可将该过程分为选择遇险船,搜救船发出遇险船的求救信息,救助水域救助船的位置选择,构建救助站救助船布置位置选择模型。
2.1 目标遇险船的选择与救助模型

(1)
实际上,处于救助范围内船舶的数量通常不能确定,而对于遇险船来说,被救助越早越好,因为等待的时间越长,救援成功的可能性会越小,所以遇险船会第一时间报警,离其最近的救助船会对其施救[11]。
在确定被救助的遇险船后进入救助阶段,现选取具有代表性的救助时刻用图1表示。
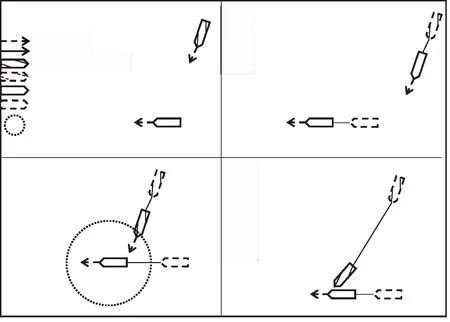
图1 救助阶段示意图
救助可分为4个阶段(如图1所示),图1(a)表示遇险船信号发出。图1(b)表示救助船向遇险船驶去,但遇险船还没有进入救助中心发布的搜寻范围。图1(c)表示遇险船进入搜救范围,救助船发现遇险船,同时也向附近的船舶发出求救信号。图1(d)表示救助船适时地赶到遇险海域,成功地救助遇险船[12]。
为了便于利用数学语言描述救助过程,需建立直角坐标系。假定遇险船的航行路线是沿y轴正向,如图2所示。
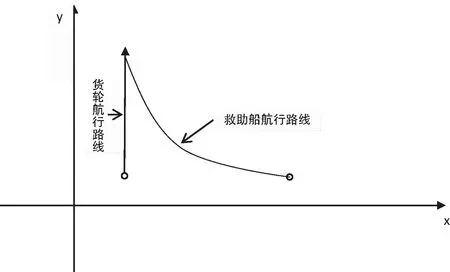
图2 遇险船与救助船航线图
假设遇险船为货轮,以遇险船发出求救信号时刻为起始时间,g点为遇险船的遇险地点,f点为货轮航行的起始点,若没有救助船救助,货轮会按图2所示航线最终进入搜寻海域。

(2)
(3)
(4)

(5)
(6)
其中,d1=d2=
最后,联立式(5)和式(6),积分后得到遇险船航向函数表达式为:
(7)

(8)
因为已经假设货轮航向与y轴平行,所以x横坐标是恒定的。将x代入遇险船航向函数可求得救助船赶到出事海域时的纵坐标。据此可计算出救助船搜寻遇险船的时间。
(9)
2.2 遇险船求救及救助船救助模型
计算遇险船从遇险到进入搜寻范围的时间,从而求出救助船最大可用救助时长。
当遇险船进入搜寻范围时,两船间达到警戒半径距离,其数学表达式为:
(10)

(11)
(12)
然后求得:
(13)
求解式(12)后得到多个结果,导致式(13)也有多个结果,在此,选取最小的t′作为触发遇险船警戒的解,得到救助船的最大可用救助时间为:
tji=t-t′。
(14)
2.3 重点海域全覆盖的救助位置选取模型
对遇险船的目标选择过程与救助过程进行分析模拟后,可得到最可能发生险情的遇险船航行地点。因为遇险船的始发港及航线有不确定性,所以需要多次模拟分析,计算出从不同港口出发、不同航线的船舶险情多发海区地点,从而选取出重点海域。
(15)
推导得到救助船的救助时间为:
(16)
将tjr、tjh做差得到
Δtjih=tji-tjh。
(17)
假设用变量Zi来衡量救助效果,并令其取值范围为[0,1]。当Δtjih≥0,表示救助船会及时赶到事发海域,科学施救。完成一次成功救助时,则Zi=1;如果Δtjih<0,救助失败,则Zi=0。同时,为了提高海上救助策略的成功率和抗风险能力,Δtjih的数值越接近1表明救助协调中心处置突发事件的能力越强。为此,设置一个合理预留时间量,使Δtjih大概率地大于该预留时间量。假设用变量ωi表示救助预留时间量,其取值范围为[0,1],若Δtjih=0,则ωi=1,反之ωi=0。
所以,遇险船舶的目标方程可定义为
(18)
(19)
这是一个两航段的海区位置选择模型,在第一航段θ不变的前提下,首先以式(18)作为遇险船的目标方程进行求解,然后以该初解结果对式(19)进行求解。
2.4 模型分析
基于重点海域覆盖的救助站的救助船布置位置模型可采用以下5个步骤进行构建:
第一步,根据搜救中心数据平台获取的遇险船和事发海域附近船舶的位置坐标及航速的最新信息,随机生成遇险船事发地的救助船位置作为模型的初始数据[13]。
第二步,根据遇险船目标的选择与事发地海域附近船舶模型,将第一步获取的数据代入第二步,计算出事发海域多艘船舶中最可能的目标遇险船及其船位,给出救助站的救助船可利用的最大赶往事发地的救助时间。
第三步,将所选取的事发海域按一定长度间隔划分成网格,以式(18)为遇险船的目标方程,运用遗传算法求出该海域救助站多艘救助船的最优救助位置,使救助点覆盖率达到100%且救助站位置为最优。
第四步,根据遗传算法求解的结果,采用贪心算法进行改进,统计小于最优的结果经改进后是否能提高救助点覆盖率,从而实现重点海域救助范围的全覆盖[14]。
第五步,在第四步遗传算法求解结果的基础上,计算所有Δtjih的结果。若该结果大于救助预留时间,则计算结果为模型最优结果;若结果小于该时间,则以式(19)为救助目标方程运用贪心算法进行改进,直至ξ的值接近0。
3 案例分析
选取威海成山角附近海域作为实例研究区域,按照构建模型的假设,选取37°23′N,122°42′E作为坐标原点,以向东方向作为角的始边,沿逆时针方向转98.32°后的终边作为y轴方向,采用n mile作为坐标轴的基本单位。选取2018年8月8日12:00位于该水域的船舶作为研究对象,根据成山角交管中心(VTS)统计数据,最终确认42艘船舶的信息数据符合模型条件,在该基础上进行案例研究。
在多发海难事故的报告线以南海域随机抽取成山角海域100个纵坐标,选择纵坐标对应的海域位置为遇险船船位。生成的纵坐标对应成山角VTS报告线内、外水域的位置。
按照1 n mile的长度间隔在所建坐标区域划分网格,从已有备选海域选择救助船初始位置,运用遗传法(变异率为0.05,交叉率为0.3,迭代数为200次),利用MATLAB软件进行计算,从救助站选取1艘救助船船位为始点,逐步增加救助船分布范围内的数量,求得该救助站多艘救助船情况下的最佳救助效果,计算结果如表1。从表1看出当救助站在该海域部署4艘救助船时,救助覆盖率为97%,当部署5艘救助船时,救助覆盖率100%。

表1 利用遗传法计算得到的救助船艘数与救助覆盖率

(20)
为了提高救助范围覆盖率,基于案例中改进计算方法的原则对救助站位置进行改进,计算结果表明,在救助站布置4艘救助船时,该海域救助覆盖率仍然是97%,因此要想将救助成功率控制在最高水平(100%),救助站需部署5艘救助船才能实现及时救助。
另外,可以根据改进策略的第二点,提高救助船驶抵事发地点的预留处置救助时间。选择一组遗传算法初始计算结果(6,145),(3,72),(2,-8),(25,353),(15,226),(5,275),(35,297)进行改进,经过改进后的救助船位置为(5.009 5,140.054 7),(2.986 7,74.590 5),(2.058 3,-9.238 5),(25.108 6,354.026 4),(16.824 2,228.813 3),(6.894 6,274.918 5),(34.604 6,297.858 8)。对比救助船的初始和改进后的位置,发现救助站救助船的布置位置略微有了调整。
将救助船的初始位置和改进后的位置相比较发现,如果采用初始的救助站救助船布置位置,将使最大救助时长与实际救助时长差值保持在0.1 h以内,从而给救助站救助船的实际施救工作造成很大压力。而经过改进后的救助船布置位置可以使救助行动的施救时间小于最大可用救助时间(0.1 h),这充分证明该模型和算法具有一定的可靠性和实用性。
4 结语
针对海上救助这一难题,构建基于重点海域覆盖理论的救助站救助船位置布置模型,将遗传算法和贪心算法相结合,用于救助船船位选择,提出适用救助船选址的新的计算方法,采用威海成山角海难事故多发水域作为案例进行计算,获取案例海域需要布置的救助船艘数及其相应的位置。结果表明建构的模型及算法均具有合理性与可靠性。
因为海难救助受到诸多因素影响,尚有许多变量需要引入,因此,构建考虑更多影响因素在内的更加合理的救助站救助船位置布置模型是今后深入研究的课题。

