抓住典型 寻找策略 用好方法

文／杨广清

“统计与概率”是中考的必考知识。各地对“统计与概率”的考查，分值比较稳定，但呈现的方式多种多样。因此，我们对“统计与概率”的复习就显得尤为重要。下面就让我们一起来看一下相关典型问题的解题策略。

一、相关概念的理解

这类问题主要考查同学们对身边事物的关注，对统计与概率相关概念的理解，解题时要注意用数学思想和方法去分析问题。

例1下列说法正确的是（ ）。

A.“打开电视机，正在播放《新闻联播》”是必然事件

B.“明天下雨的概率为0.5”，是指明天有一半的时间下雨

C.一组数据“6，6，7，7，8”的中位数是7，众数也是7

D.甲、乙两人在相同的条件下各射击10次，他们成绩的平均数相同，方差分别是，则甲的成绩更稳定

【解析】利用随机事件的定义、概率的意义、中位数及众数的定义、方差的意义分别判断即可确定正确的选项。故选D。

二、利用概率公式直接计算

这类问题往往以实际问题为背景，贴近我们的生活，旨在考查同学们对简单随机事件概率问题本质的理解，此类试题的概率求法如下：如果一个事件有n种可能，而且这些事件发生的可能性相同，其中事件A出现m种结果，那么事件A出现的概率

例2如图1，有4 张形状、大小、质地均相同的卡片，正面印有速度滑冰、冰球、单板滑雪、冰壶四种不同的图案，背面完全相同。现将这4 张卡片洗匀后正面向下放在桌子上，从中随机抽取一张，抽出的卡片正面恰好是冰壶项目图案的概率是（ ）。

图1

【解析】我们先找出冰壶项目图案的张数，再根据概率公式即可得出答案。因为有4张形状、大小、质地均相同的卡片，印有冰壶项目图案的有1 张，所以，从中随机抽取一张，抽出的卡片正面恰好是冰壶项目图案的概率是故选A。

三、几何概率模型

这类问题是将几何概率模型转化为古典概率模型，利用图形面积比求概率。解决这类问题的关键是准确地算出阴影部分的面积。

例3一个小球在如图2 所示的方格地砖上任意滚动，并随机停留在某块地砖上，每块地砖的大小、质地完全相同，那么该小球停留在深色区域的概率是 。

图2

【解析】若将每个方格地砖的面积记为1，则图中地砖的总面积为9，其中深色区域的面积为2，所以该小球停留在深色区域的概率是故答案为

四、统计图的设计

解决这类问题需要同学们具有丰富的生活经验，对能力要求较高。我们要先理解数据收集与整理的完整过程，再分清制作步骤，最后作答。解题的关键是熟悉统计图的制作步骤。

例4舒青是一名观鸟爱好者，他想要用折线统计图来统计中华秋沙鸭每年秋季到当地避寒越冬的数量变化情况，以下是排乱的统计步骤：①从折线统计图中分析出中华秋沙鸭每年来当地避寒越冬的变化趋势；②从当地自然保护区管理部门收集中华秋沙鸭每年来当地避寒越冬的数量记录；③按统计表的数据绘制折线统计图；④整理中华秋沙鸭每年来当地避寒越冬的数量并制作统计表。正确统计步骤的顺序是（ ）。

A.②→③→①→④

B.③→④→①→②

C.①→②→④→③

D.②→④→③→①

【解析】本题是一道折线统计图的制作步骤。正确的步骤是：收集数据，整理数据，按统计表的数据绘制折线统计图，从折线统计图中分析出中华秋沙鸭每年来当地避寒越冬的变化趋势。故选D。

五、统计与概率综合题

这类问题需要大家从统计表中获取有效信息，关键要认真读题，仔细审题，耐心译题，精心破题。只要能够从复杂的信息中提取有效信息，再对信息进行加工与利用，解决这类问题就可以水到渠成。

例52021 年是中国共产党成立100 周年。为普及党史知识，培养爱国主义精神，当年五月份，某市党校举行党史知识竞赛，每个班级各选派15 名学员参加了网上测试，现对甲、乙两班学员的分数整理分析如下：

甲班15名学员测试成绩（满分100分）统计如下：

87，84，88，76，93，87，73，98，86，87，79，85，84，85，98。

乙班15名学员测试成绩（满分100分）统计如下：

77，88，92，85，76，90，76，91，88，81，85，88，98，86，89。

（1）按下表分数段整理两班测试成绩：

班级甲乙70.5~75.5 1 0 75.5~80.5 2 3 80.5~85.5 a 3 85.5~90.5 5 6 90.5~95.5 1 2 95.5~100.5 2 1

表中a=________；

（2）补全甲班15 名学员测试成绩的频数分布直方图；

（3）两班测试成绩的平均数、众数、中位数、方差如表所示：

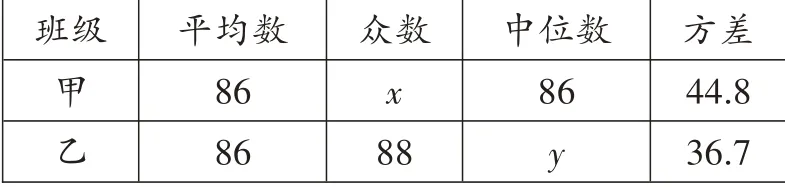
班级甲乙平均数86 86众数x 88中位数86 y方差44.8 36.7

表中x=________，y=________。

（4）以上两个班级学员掌握党史相关知识的整体水平较好的是________班；

（5）本次测试两班的最高分都是98 分，其中甲班2 人，乙班1 人。现从以上三人中随机抽取两人代表党校参加全市党史知识竞赛，利用树状图或表格求出恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率。

【解析】此题考查了列表法或画树状图法求概率、频数分布直方图、统计表、众数、中位数等知识。列表法可以不重复、不遗漏地列出所有可能的结果，适合两步完成的事件；画树状图法适合两步或两步以上完成的事件。解题时要注意此题是放回试验还是不放回试验。

（1）由甲班15 名学员的测试成绩即可求解a=4。

（2）由（1）的结果，补全甲班15 名学员测试成绩的频数分布直方图如下：

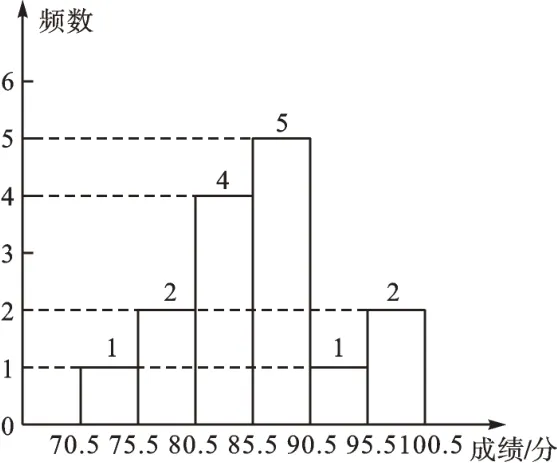
（3）由众数、中位数的定义求解即可。故答案为：87，88。

（4）从平均数、中位数、方差几个方面说明即可，以上两个班级学员掌握党史相关知识的整体水平较好的是乙班。理由如下：

①甲、乙两个班的平均数相等，但乙班的中位数大于甲班的中位数；

②乙班的方差小于甲班的方差，因此乙班的成绩更稳定。

故答案为：乙。

（5）画树状图，共有6 种等可能的结果，恰好抽取甲、乙两班各一人参加全市党史知识竞赛的结果有4 种，再由概率公式求解即可。把甲班2人记为A、B，乙班1人记为C，

画树状图如图：

共有6 种等可能的结果，恰好抽取甲、乙两班各一人参加全市党史知识竞赛的结果有4 种，所以恰好抽取甲、乙两班各一人参加全市党史知识竞赛的概率为