小型无人机遥控器信号参数估计方法∗

陈 林 唐文波 丁学科 樊 荣

（1.同方电子科技有限公司 九江 332000）（2.中国民用航空飞行学院航空电子电气学院 广汉 618307）

1 引言

近年来，各类民用无人机已在农业、电力、测绘、航拍、疫情防控等领域发挥着重要作用［1］。然而小型无人机具有易制造、易获取、易改装、易使用等特点，使得对小型无人机改装等行为难以监管，因无人机非法应用导致的安全事件日益增多。同时，由于小型无人机具有典型的“低-慢-小”目标特性，当前的无人机信号检测技术尚存在诸多问题，需要研究新的无人机目标检测技术以解决对无人机目标信号检测、识别和管控问题。

目前无人机目标检测技术主要有雷达检测［2］、声波检测［3］、光电检测［4］等手段，但上述各检测手段均存在技术缺陷。具体上讲，雷达检测需主动发射探测波形，在民航机场净空区域无人机目标探测应用中存在无线电频谱兼容问题，且无人机回波特征与飞鸟回波特征相似，目标难以辨识。声波检测技术手段主要凭借无人机在工作时电机（或旋翼）产生的声音信号（一般涵盖300Hz～20KHz频率范围），利用声纹识别技术对无人机目标检测和识别，但该类方法的目标探测距离一般在几十米范围内。光电检测技术手段主要利用可见光/红外成像技术通过图像识别算法实现无人机目标检测，该类技术受实际光线、温湿度等环境因素影响明显。与上述几种检测手段不同，利用无人机与遥控器间的控制信号对无人机目标检测，具有显著的技术优势［5］。当前小型无人机遥控器信号频率主要集中在 IEEE 802.11 WLAN 工 作 频 段［6］（2.4GHz～2.483GHz频率范围），普遍采用跳频扩谱（Frequen⁃cy-Hopping Spread Spectrum，FHSS）用频方式。通过提取无人机遥控器信号的跳频速率、跳频时刻、跳频频率等特征可有效检测无人机目标，对无人机遥控器信号跳频参数估计已成为当前无人机目标信号检测与识别的重要技术手段［7～8］。

针对跳频扩谱（FHSS）信号检测，代表性方法主要是基于时频分析的信号检测法。在该类方法中，作为最具代表性的短时傅里叶变换（Short Time Fourier Transform，STFT）法已被广泛应用于跳频信号参数估计中，该方法属于线性时频变换分析方法范畴，具有运算复杂度低、实时性高等优点，但对信号参数的估计精度不足［9］。在此基础上，He Y.等人提出了一种跳频周期和跳频频率联合估计方法，提升了跳频信号参数的估计性能，但该方法仍然属于线性时频分析方法，所能获得的信号时频分辨能力有限［10］。对此，Barbarossa采用维格纳-维利分布（Wigner-Willie Distribution，WVD）估计信号的跳频频率和跳频时刻，提升了对信号的时频分辨能力，但多个信号同时存在时，该方法会产生交叉干扰项问题，从而限制了该方法的信号特征提取能力［11］。鉴于上述问题，新的基于伪维格纳-维利分布（Pseudo Wigner-Willie distribution，PWVD）［12］和平滑伪维格纳-维利分布（Smooth Pseudo Wigner-Willie Distribution，SPWVD）［13］的时频分析检测方法被相继提出，抑制了交叉项干扰，进一步提升了对调频信号的时频特征分析能力，然而这两种方法存在时频聚集性不高的问题，在实际应用中受到一定限制。为提升时频聚集性，张曦等基于Gabor变换提出了一种对跳频信号参数估计的时频分析方法，该方法在消除交叉干扰项的同时保留了信号的时频聚集特性，然而所提方法的计算复杂度高，难以应用在高实时性要求场景中［14］。为进一步提升时频分析性能，付卫红等将STFT和SPWVD相组合，提出了一种新的时频分析方法［15］，此外，Stock⁃well R G等人基于S变换也实现了对跳频信号参数提取并获得了不错的性能［16］。然而上述各类信号检测方法未设计专门的噪处理环节，对此刘若兰等在时频分析基础上引入门限降噪策略对噪声进行抑制，提高了信号时频参数估计性能［17］。需指出的是由于检测方法中人为引入了降噪门限，设置的静态门限难以应对复杂动态变化的信号检测场景。

考虑到当前各类跳频信号参数估计方法均存在各自缺点（时频参数估计性能差，计算复杂度高，或环境适应能力弱等），本文针对无人机遥控器信号检测应用场景，提出了一种计算复杂度低且检测性能好的跳频信号参数估计新方法。所提方法无需计算无人机跳频信号的时频分布信息，而是基于频域互相关运算降低了检测方法的计算复杂度。同时，在信号参数估计中无需预先人为设定门限阈值，通过分析相邻段采样信号的频域相关性即可检测信号频率是否发生跳变，提高了跳频信号特征估计性能。

2 跳频信号模型

工作在2.4GHz频段的小型无人机遥控器信号普遍采用跳频通信模式，跳频信号是一种典型的非平稳信号，其载波频率通常按照通信双方约定的规律随着时间跳变。单个跳频信号的载波频率在某一跳频周期内保持不变，所有可能出现的载波频率构成了该跳频信号的跳频频率集合，典型跳频信号的时域模型如下［18～19］：

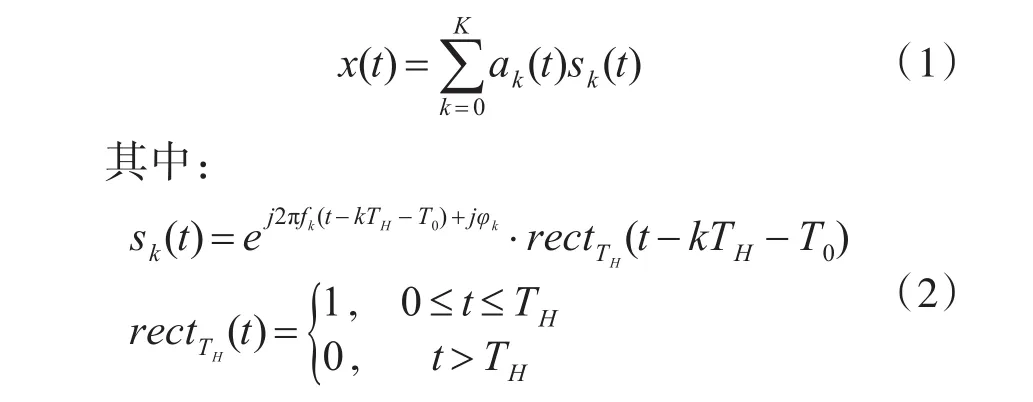
式（1）中的K为跳频次数；ak(t)为分配到第k个跳频载波频率上的基带信号；式（2）中的sk(t)、fk、φk分别表示第k个跳频信号分量及其瞬时频率和初始相位；rectTH(t)表示宽度为TH的门函数；TH为跳频周期；T0为起跳时刻。

在均值为0方差为σ2的复高斯白噪声噪声场景（记噪声为v(t)）中，经过对信号离散采样后的N点离散信号观测值建模为

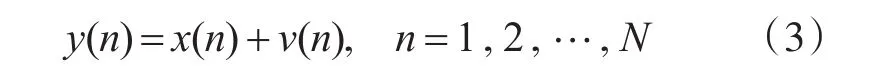
其中，随机噪声v(n)～(0，σ2)。

3 跳频信号参数估计方法

考虑到基于STFT的时频分析方法具有复杂度低，实时性高等有点，本文选取了两种基于STFT为基础的代表性时频分析方法作为所提方法的对比方法。在具体给出两种传统检测方法之前，STFT及时频图计算表达式。

对于任意给定的离散时域信号序列｛y(n)|n=1，2，…，N｝，其短时傅立叶变换计算式可通过式（4）得到［22］：

式中h(l)为窗函数；Len为窗口的宽度；l表示离散时间点；u表示离散频率点。将STFT结果取模平方的结果定义为时频谱图，数学模型表示为

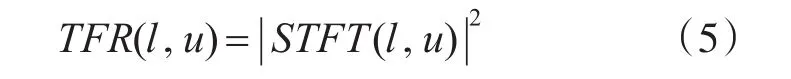
1）方法1：基于时频脊线的跳频参数估计

在该方法中，通过提取时频脊线得到无人机跳频信号在不同时刻的频率值，将不同频率值间的时间间隔作为信号的跳频周期值，其倒数即为跳频速率，并将频率值发生改变的时刻记为跳频时刻；取信号某一跳的跳频周期内所有频率值的均值作为该跳信号的频率值。基于时频脊线的跳频参数估计法算法流程如图1所示。

图1 基于时频脊线的跳频参数估计法

2）方法2：基于最大值图的跳频参数估计

基于最大值图的跳频参数估计法中，首先沿时隙逐点找出频率轴上的最大值，得到具有周期性的最大值图R(m)，在此基础上计算相邻峰值间的距离作为信号跳频周期的估计值；然后利用二次差分算法估计每跳信号的中心时刻；最后通过每跳的中心时刻进一步估计出跳频时刻集和跳频频率集。完成对无人机遥控器调频信号的参数估计。该检测方法的算法流程如图2所示。

图2 基于最大值图的跳频参数估计法

3）所提方法：基于频域互相关的跳频信号参数估计

注意到同一架无人机跳频信号的每跳信号具有相同带宽，利用频域互相关处理可在频域上获得高相似性的能量分布特征，因此基于该特性可以完成对无人机遥控器跳频信号参数估计。通过预先在时域上按时隙分割信号进而分析相邻信号的频域相关性，即可判定信号频点是否发生跳变，进而估计出无人机跳频信号的各类特征参数。为展示该特性，下面基于前文给出的跳频信号模型生成仿真数据，假设无人机遥控器信号的频率变化范围为20KHz～80KHz，频率间隔为15KHz，跳频周期为2ms，采样频率为400KHz，采样时间为0.1s，信号划分时隙为1ms（对应样本点数L为400），信噪比为0dB。

基于上述参数场景计算了同一架无人机相邻跳信号的频域图及其频域相关结果，图3为仿真结果。同时，还计算了同一架无人机信号在相同跳内不同时刻的频域图及其频域相关结果，图4为仿真结果。

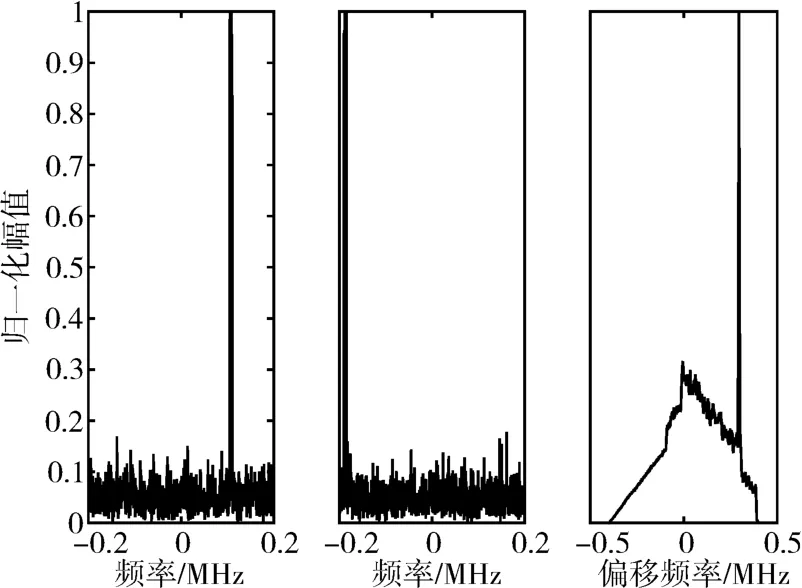
图3 相邻跳的跳频信号频域及频域相关结果图

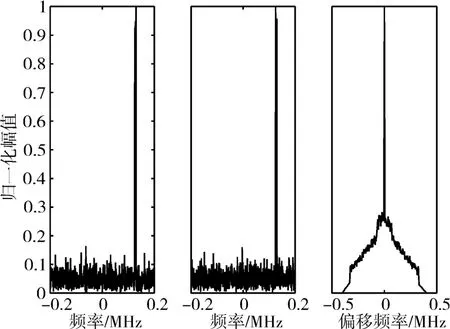
图4 同一跳的跳频信号频域及频域相关结果图

图3 和图4的仿真计算结果表明：当信号频域相关结果中的峰值出现在零频点附近时，则两段信号属于同一跳信号内的前后相邻时隙信号；而峰值出现在非零频点时，则表明前后两段信号的频率发生了跳变，即两段信号具有不同频点。基于上述特征，下面给出一种基于信号频域互相关的跳频信号参数估计方法，所提方法详细的信号参数估计流程如图5所示。

图5 基于频域互相关的跳频参数估计法

4 仿真实验与分析

4.1 评价指标

为评价所提方法的跳频信号参数估计性能，使用相对误差（Relative Error，RE）作为跳频速率参数估计的评价指标，相对误差定义式如下。

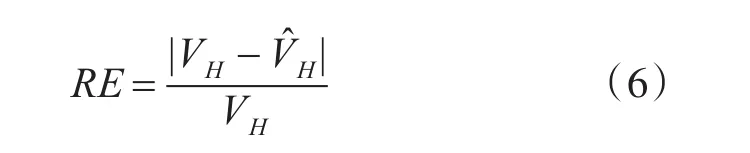
式中为跳频速率估计值，VH为真实跳频速率。

使用为评价所提方法的跳频时刻集和跳频频率集参数估计性能，文中使用均方根误差（Root Mean Square Error，RMSE）作为评价指标，定义式为

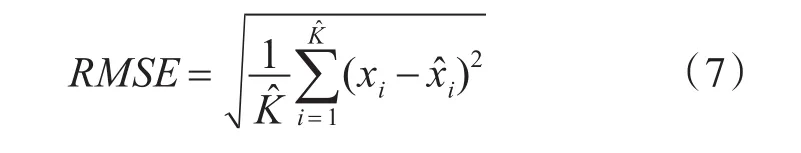
4.2 仿真实验

仿真场景设置如下：跳频信号的频率变化范围为20KHz～80KHz，频率间隔为15KHz，跳频周期为2ms，采样频率为400KHz，采样时间为0.1s，信噪比变化范围为-10dB～8dB，在每个信噪比场景下进行1000次蒙特卡洛仿真实验。

三种方法的计算耗时如图6所示，跳速估计误差、跳频时刻集估计均方根误差、跳频频率集估计均方根误差分别如图7～图9所示。

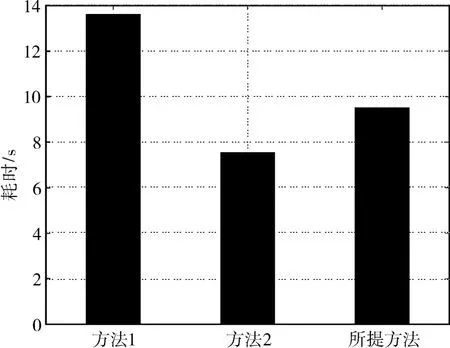
图6 三种方法计算耗时（1000次蒙特卡洛）

从图7的跳频速率估计误差结果中可以得知，所提方法在信噪比极低的场景下性能与方法1和方法2相当，但当信噪比大于-2dB时，前者对跳频速率参数的估计性能大幅提升，且当信噪比大于2dB后误差达到了最小值并趋于稳定。

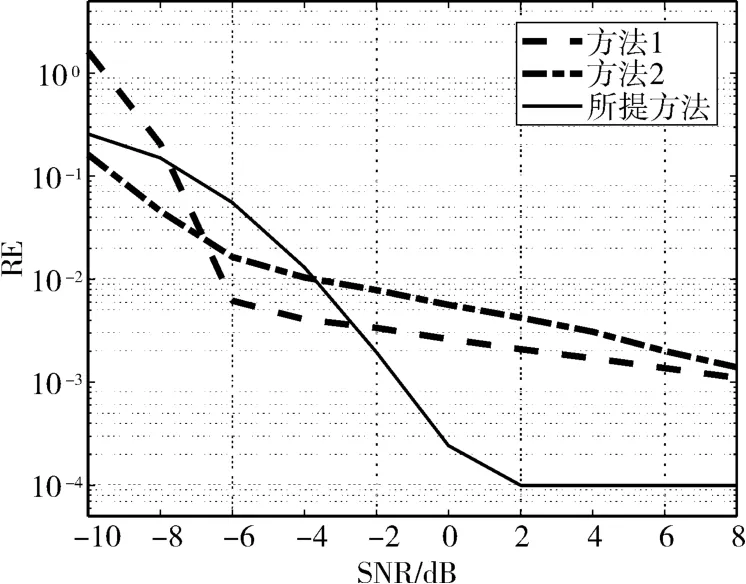
图7 跳频速率估计误差

图8中的跳频时刻集估计均方根误差结果表明：所提方法的性能几乎全面优于方法1和方法2。与方法1和方法2不同，所提方法在信噪比大于-6dB的场景下，对跳频时刻集参数的估计性能显著提升。

图9为三种方法对跳频频率参数的估计结果，传统方法的估计误差在极低信噪比下有着极大的误差，当信噪比达到-6dB时性能得到巨幅提升，这直观地反映出阈值的设定给传统方法带来的弊害。而所提方法对噪声的敏感度较低，当信噪比大于0dB后参数估计性能趋于稳定且优于传统方法。

图9 跳频频率集估计误差

仿真结果表明当信噪比大于-2dB时，本文所提方法在跳速参数估计、跳频时刻集参数估计、跳频频率集参数估计上全面优于方法1和方法2，对无人机跳频信号的特征参数有着优秀的估计性能，并在信噪比大于2dB时，参数估计性能趋于稳定。

5 结语

本文为提高跳频信号特征参数估计性能，针对跳频信号中每跳信号的频率特征，提出了一种基于频域互相关的跳频信号特征参数估计方法。该方法与传统的时频分析方法相比，在降低运算量的同时解决了由于阈值的设定导致在低信噪比场景下带来的检测性能下降的问题。仿真结果表明，本文所提方法对跳频信号的跳频速率、跳频时刻集、跳频频率集的估计性能优于传统的基于时频脊线的特征参数估计法和基于最大值图的跳频参数估计法。接下来主要研究工作是利用所提方法在采样带宽受限条件下实现无人机跳频信号检测与参数估计。