无人车辆路径规划算法发展现状∗

王 涛 黎玉康 刘文学

（陆军炮兵防空兵学院 合肥 230000）

1 引言

无人驾驶车辆通过传感器感知周遭环境，并对自身定位，建立起基本的外部环境模型，按照既定的任务目标，控制自身的前向速度和转向角，达到避开障碍，抵达目标点位的目的。无人驾驶车辆的运行经过以下几个关键步骤：信息感知、决策、控制实施。其中，决策将前后两个关键性的步骤连接起来，为无人驾驶提供了基本条件，而路径规划正是决策过程中的重要一环。路径规划是指无人驾驶车辆在一定的复杂环境中，根据环境信息规划出能够从初始点位到达目标点位的曲线，该曲线应满足车辆的运动学特性以及其他附加约束。为了更好地（经过路径最短、消耗功率最小、最安全、最方便实现等）抵达目标点位，发展出了各类不同的路径规划算法。根据获得的环境信息程度，可将路径规划算法分为两类：全局路径规划和局部路径规划。

2 全局路径规划算法

全局路径规划是在对环境整体布局完全已知的条件下的路径规划方法，意在找出满足某些条件的最优解。全局路径规划算法有很多，大致可分为传统算法、智能算法，随着路径规划的发展也逐渐衍生出传统算法与智能算法相结合的混合算法。传统算法较为基础，但作为其代表的A*算法历久弥新，是一大研究热门。智能算法多是人们为了解决自然问题，模拟自然的产物。本文挑选了作为进化智能算法代表的的遗传算法，集群智能算法的蚁群算法，以及综合了进化和集群智能的粒子群算法。

2.1 A*算法

A*算法Dijkstra算法的基础上加入了启发函数和预估代价的一种启发式算法，广泛应用于静态环境下的最短路径直接搜索。公式表示为

其中f（n）是从初始点经由节点n到目标点的估价函数，g（n）是在状态空间中从初始节点到n节点的实际代价，h（n）是从n到目标节点最佳路径的估计代价。保证找到最短路径（最优解的）条件，关键在于估价函数f（n）的选取：估价值h（n）＜=n到目标节点的距离实际值，这种情况下，搜索的点数多，搜索范围大，效率低。但能得到最优解。并且如果h（n）=d（n），即距离估计h（n）等于最短距离，那么搜索将严格沿着最短路径进行，此时的搜索效率是最高的。如果估价值＞实际值，搜索的点数少，搜索范围小，效率高，但不能保证得到最优解［1］。

陈鑫鹏［2］等提出了等步长分层拓展的方法，减少车辆后退以及转弯，采用Dijkstra算法得出的n点到终点的距离作为启发式，增加了倒退惩罚的代价机制，减少了冗余节点的参与计算，提高了算法效率，路线经过优化拟合，大幅提升了行驶的平稳性以及可行性。刘子豪［3］等结合跳跃点搜索理论，优化子节点的选择，减少了计算量，在二次计算中消去了转角区域的不必要节点，缩短了路径长度，减小了路径转弯处的曲率，提高了无人车辆通过的平稳性。李世国［4］等采用了双向A*算法，从起始点和目标节点同时相向开始搜索直至重合，大大提高了计算效率，并在障碍物周围设置缓冲区，引入风险系数，越靠近障碍物，系数越高，最高为1，引入预估距离，实际距离，风险系数的权重参数，根据实际情况调整权重，提高了算法的适应性。唐碧君［5］等为了解决传统A*算法使得无人车辆容易出现不必要的转向和与障碍物产生碰撞的问题，提出了改进混合A*算法，分三个阶段优化路径，先计算出有可行性的通畅路径，再构建吸引力与排斥力的航路点环境，最后结合车辆转弯半径，对路径曲线的曲率进行约束，得出更平滑，安全的路径曲线。闵海涛［6］等根据非结构化环境的特点，提出了全球导航层与局部规划层相结合的环境描述方法，并提出了基于非结构化环境中自动驾驶车辆A*算法的改进型局部运动规划算法。在改进的算法中，通过设置安全空间避免了轮廓碰撞，在启发式功能设计中考虑了路径曲率的成本。与原始算法相比，它可以提高路径的平滑性，从而使路径更符合车辆运动特点。

2.2 遗传算法

遗传算法的基本思想脱胎于达尔文的进化论和孟德尔的遗传论，其流程框图如图1所示。

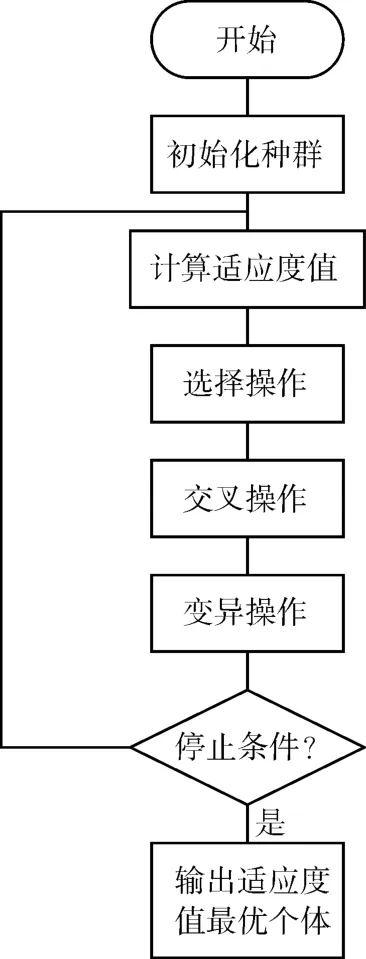
图1 遗传算法框图

假设一个初始解集，将每个解视为染色体不同的个体，将其置于一系列的约束条件之中，按照物竞天择，适者生存的原则，筛选出表现较为良好的个体，将其复制，交叉，变异产生新一代的个体集，通过一代代进化筛选，最终得到最适应约束条件的个体也就是最优解。但是此类算法在环境偏复杂时，结果收敛速度较慢，无法确定精确最优解，算法的参数难以定量等不足。但是它依然具有宽广的前景和很大的潜力，吸引了众多学者展开研究。

黄书召［7］等提出了混合无重串选择算子，使得假设的初始解集有了一定的扩增，增加了适应性好的解的数量，令收敛解更接近于最优解，但同时也使得收敛速度变慢，为了解决这个问题，他们同时提出了非对称映射交叉算子和启发多次变异算子。徐梦颖［8］等通过提高传统遗传算法免疫克隆性，将解的质量与被复制数相对应，指出了最优解的收敛方向，提高了收敛速度，并加入自适应参数从而避免陷入局部最优解。李昌华［7］等在遗传算法中采用元胞自动机邻域模型，利用元胞的隐性迁移机制，使得在进化演变过程中，多样化的解得以留存，收敛解更加接近最优解，在路径选择中增加了平滑因素的影响，使最终路径更适应车辆行驶特性，提高了路径质量。Tobias Rainer Schafle［10］等考虑到路径最短但实际能量消耗不一定最少的情况，在传统遗传算法中提出了能量评估适应度函数，对无人车辆按照既定路径加减速，转弯掉头等形式的动作消耗的能量作出估算，给出更符合经济实际的最优路径。陈宣刚［11］等令遗传过程中的交叉概率和变异概率随着进化个体的变化而变化，加大了优胜劣汰的竞争强度，有效地保存了优势个体，这种自适应遗传算法实现了更快的解算速度。

2.3 蚁群算法

蚁群算法于1992年被首次提出，其创始人意大利学者Dorigo等在蚂蚁觅食行为中得到灵感，如图2所示。

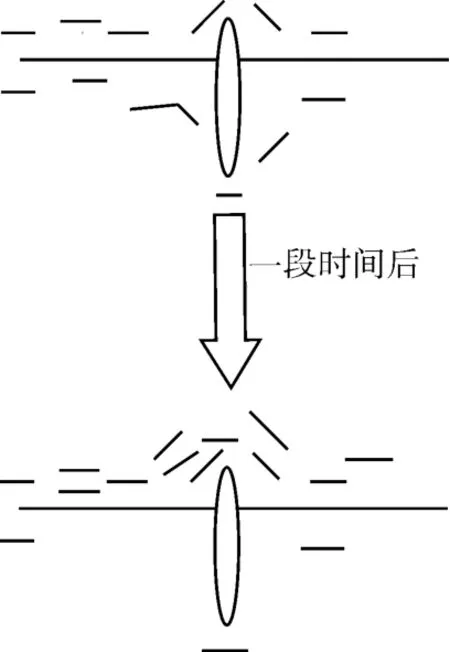
图2 蚁群觅食行为简图

蚂蚁在觅食的路径上会留下信息素，当找到食物，蚂蚁原路返回，该路径上的信息素浓度将明显高于其他没有找到食物的路径，后来的蚂蚁选择路径的概率随着信息素浓度的增高而增加，且信息素有挥发性，使得有食物的路径上信息素浓度与没有食物路径上的信息素浓度差距越来越大，而有食物的路径中，路程越短的路径单位时间内通过的蚂蚁越多，信息素浓度越高，导致最终蚂蚁的路径趋向于最近的食物路径。蚁群算法在全局优化方面效果良好，且鲁棒性强，但同时也有计算量大的缺陷，且由于信息素的累计容易导致局部最优解。

王苏彧［12］等将传统的定常数信息素挥发因子跟改为随时间变化的服从Laplace分布的信息素挥发因子，削弱了前期以及后期挥发因子的作用，提升了算法速度，增强了中期挥发因子的作用，加强了算法路径的多样性，保证了结果的最优性。在启发函数中加入加权系数，避免陷入局部最优解。仿真验证此改进蚁群算法明显优于传统算法。徐玉琼［13］等提出变步长蚁群算法，将传统蚁群算法中的单步长扩展为除了有障碍存在以外的的全局环境选择跳点，提高了路径搜索效率，信息素初始浓度从四周向始末点连线附近逐步增加，减少了无效路径选择，通过设置信息素浓度上下限的方式避免了局部最优解，优化了启发函数，提高了算法的收敛速度，该算法收敛速度较之传统算法大幅提高，且在复杂环境下也能有较好的表现。桑和成［14］等提出了转角启发因子，令路径选择的有效性大大提高，减少了转角过大而产生绕路的情况，引入估价函数思想，对下一节点与目标节点的距离进行评估，缩小了路径搜索范围，提高算法效率。王苗苗［15］等先通过A*算法对路径进行初步搜索，按照得出的初步结果给出信息素的分布，解决了蚁群算法初期盲目发展的问题，加快了整体的收敛速度，建立了信息素的影响系数和挥发系数的自适应模型，使得该系数随着算法的进行不断自我调整，推动算法进行且避免了局部最优。周东升［16］等在空间避障规划中给定蚁群算法的路径选择以X轴为主要方向，规定了蚂蚁最大的横向和纵向移动距离，减化了蚂蚁搜索下一个节点的搜索空间，对于下一节点的选择除了信息素影响的确定概率外，加入了增加算法多样性的随机概率，信息素的衰减系数以及更新系数通过蚂蚁搜索完成路径的长度进行实时更新。根据仿真结果显示，该算法运行时间更短，避障效果更好。但是该算法依然无法解决更复杂的环境或者动态非结构化环境下的避障问题。

2.4 粒子群优化法

粒子群优化法起源于人们对鸟类觅食行为的探索，其流程框图如图3所示。

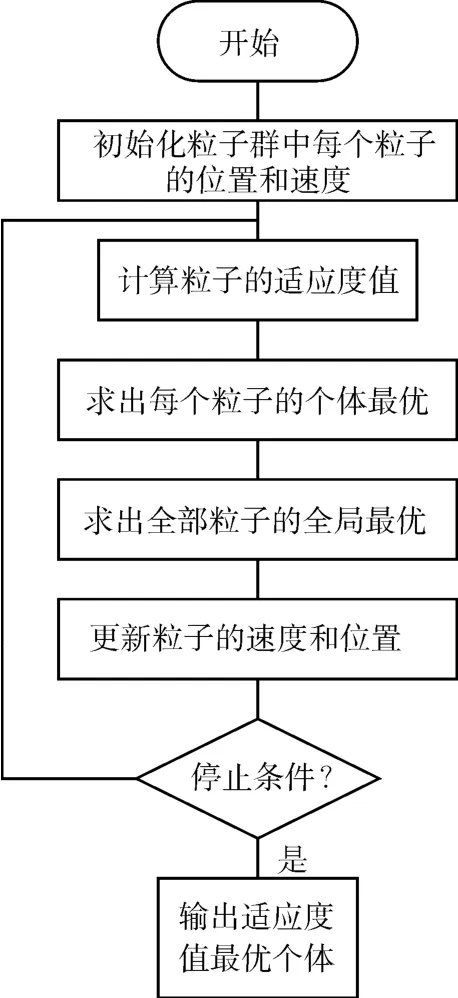
图3 粒子群算法框图

每只鸟看作一个有速度和位置信息的粒子，每个粒子找到食物后将自己的路径信息与同类共享，通过与同类比较，选取更近的路径，多次比较迭代后，得到最优解。粒子群优化算法具有收敛速度快，鲁棒性强，精度高等优点，但也容易造成收敛过早，局部最优解的问题。

李学军［17］提出了反向学习粒子群的方法应用于机器人的多目标路径选择，通过调整目标函数与偏差常函数的权重系数来实现最短路径的同时避免与障碍碰撞，该算法模型简单，计算速度较快，能够满足机器人实时替换目标点并选择路径的需求，具有一定的实用价值。付兴武［18］等将粒子群优化算法与天牛须算法结合，将每个粒子加入天牛会对环境进行自我判断的能力，避免了粒子群算法易于陷入局部最优解的问题，规划效率更高，路径更优。杨红果［19］等将传统粒子群算法与遗传算法相结合，对每个有完整路径的粒子的路径进行编码，该编码视为粒子基因，将路径最短的粒子个体的基因与其他个体交叉，将每个粒子按照一定的概率进行混沌优化，有效克服了传统粒子群算法易于陷入局部最优以及迭代次数多的缺点。刘晓欢［20］等将惯性权重与迭代次数相关联，并引入递减因子，使得惯性权重对最终解的影响逐渐减小，进而产生算法初始解算范围较大，后期避免局部极值的效果，学习因子的更新公式，使得粒子群在保证良好的路径规划能力的同时有着较快的收敛速度。但该算法较为复杂，实际运用中响应较慢。P.K.Das［21］等对粒子群算法中的粒子参考遗传算法和蜂群算法的进化方式，强化粒子个体的搜索能力，同时计算每个机器人的路径坐标，在向最优化靠近的同时保证路径的多样性。

2.5 对比分析

全局路径规划算法还有优缺点以及其当前的改进方式如表1所示。

表1 全局路径规划算法的优缺点以及其改进方式

全局路径规划普遍显示出求解效率较低，易于陷入局部最优的问题，但算法的求解能力与收敛速度是一对相互排斥的性质，因此全局规划的优化改进方法主要集中于在保证算法求解能力的同时提高求解效率，和增大求解过程中解的多样性以保证最终解的优良性。

3 局部路径规划

局部路径规划属于动态规划，是指无人车辆通过传感器，实时感知环境信息，对局部环境建模，完成从当前节点到下一子节点路径的局部最优化。局部路径规划令无人车辆能够有效地应对动态复杂环境，与全局路径规划相互配合，大大提升了在实际中的应用效果。局部路径规划算法根据其特点可分为采样方法、条件约束法、机器学习法，挑选出滚动窗口算法、人工势场算法、强化学习算法分别进行概括。

3.1 滚动窗口算法

滚动窗口算法是指根据传感器感知环境，通过滚动的方式对路径作出在线规划，每滚动一步（按照上一步的规划路径），探测到新的环境信息，进而对上一步的规划作出反馈并用启发式方法优化下一步子目标的选择，并做出新的局部路径规划。如此循环达到对局部动态环境的实时路径规划效果。该算法计算量较小，对环境较为敏感，可有效避开障碍物，具有实时性。

金何［1］等运用滚动窗口法探查局部环境信息，识别障碍，选择局部子目标，通过不断接近子目标最终达到终点的目的，但是该方法难以应对更复杂的环境以及运动速度较快的动态障碍，具有较大的局限性，并且由于该方法使用昆虫算法规划接近子目标的路径，使得路径较长。孙斌［23］等建立了未知环境下，对障碍物存在的判断方法和动态障碍的预测及处理方式，设计了局部子目标的启发式函数。通过实验证明了其在未知动态环境下的良好适应性。陈明建［24］等结合了牛耕遍历方式与窗口滚动达到对未知环境信息的探测，简化了模型，提高了探测效率，借助A*算法实现局部子目标的路径以及跳出死胡同的逃逸路线。在清洁机器人上搭配360°激光传感器使用，具有算法简单，效率高，易于实现的优点。

3.2 人工势场算法

人工势场算法是指人为建立一个虚拟力场，如图4所示。

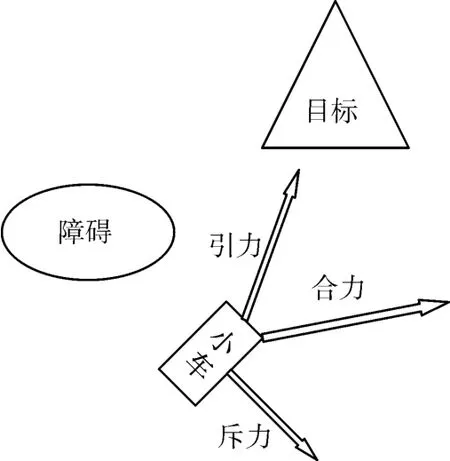
图4 人工势场示意图

车辆在环境中同时受到障碍物的斥力和目标点的吸引力，车辆受到的力的大小与其同障碍物或目标点的距离负相关，即距离越短，受力越大。无人车辆在合力的作用下，前往下一个目标点。然而人工势场算法还存在许多问题，例如在障碍物附近的目标点，其产生的合力几乎为零使得无人车难以到达，陷入局部最优；在经过狭窄路径时易产生左右震荡的问题等。因此人工势场算法不宜用于高自由度下的车辆路径规划问题。但是人工势场算法的简单结构，快速响应，规划路径平滑等特点依然吸引了众多研究学者的探索。

陈麒杰［25］等提出了改进的人工势场，在斥力函数中加入了斥力影响因子，该影响因子和目标点与障碍物之间的距离相关，避免了目标点位在障碍附近而无法达到的问题，添加了无人机之间的斥力关系，避免无人机相撞，引入了无人机群前置形心作为微弱引力源，在障碍物与目标点位产生的合力为零时，引导无人机群走出该局部最小值区。何乃峰［26］等在斥力场函数中引入位姿阈值增益，使得当无人车目标点位于障碍附近，不可到达时，改变斥力场的线性影响，使得目标点位处的势能最低，利用退火算法原理，当无人车陷入局部最小值时，重构障碍斥力函数，以一定的概率达到全局最优解。李军［27］等将传统斥力场更改为椭圆形使得路径更平滑，建立道路边界斥力场使得车辆不会偏离道路，对移动的障碍添加速度斥力场使得环境更符合实际情况。刘梦佳［28］等建立了改进的势场，该势场分为三个层次：位置势场、速度势场和加速度势场。在改进位置势场的基础上，构造了由相对速度和相对加速度组成的有源滤波器。改进的吸引场函数包括无人艇与目标产生的相对位置、相对速度和相对加速度的势场，解决了传统算法在动态障碍中容易产生局部最小值和震荡的问题。BARUKČ I［29］等结合了人工势场算法和昆虫算法的优点，当无人机遇到较大障碍斥力而无法到达目标点时，采用备用的昆虫算法，令无人机沿着障碍物的边沿运动，解决了陷入局部最小值的问题，当传感器短暂失效时，扩大障碍物斥力场影响范围，随着无人机与障碍物的距离改变障碍物的斥力场函数，保证了无人机的安全，且减少了无人机因传感器实效而导致的悬停，增加了无人机的航程。但该方法只适用于简单、少、静态障碍物的环境，面对复杂、动态障碍物效果不佳。

3.3 基于强化学习的路径规划算法

强化学习是无人车辆通过传感器与环境进行信息交互试错学习，对无人车辆应对不同环境的行为作出奖惩评判，从而不断优化行动方案达到最佳。强化学习可较好地应对复杂动态环境，但其学习能力难以提升，面对复杂环境往往计算收敛速度慢，限制了其实时局部路径规划的实际表现。

周彬［30］等提出了根据无人机探索目标源发出信号强弱获得相应的反馈，并结合玻尔兹曼概率选择无人机动作以达到路径选择的作用，利用“导向强化”原则，加快了算法收敛速度。但该方法躲避动态障碍能力较弱，只适用于单个无人机简单空旷环境下的路径规划。李辉［31］等提出了一种基于DQN的改进算法。该算法以值函数近似法代替Q-learning中的动作值函数，解决了Q-learning在状态空间较大时产生的维数灾难问题；通过构建预测网络和目标网络的双层网络结构避免模型在训练时的误差震荡和发散，保证了算法的稳定性；引入经验回放机制减少近似值函数的估计偏差，加快了收敛速度。熊俊涛［32］等引入了人工势场的思想，建立了目标吸引的奖励函数以及障碍排斥的惩罚函数，引导机器人在避开障碍的情况下，尽快达到目标点；提出了一种方向惩罚避函数及机器人碰撞分析模型，提高了无人车正确行为的激励效果，提高了收敛效率。李俊涛［33］等在DQN算法中加入了先验经验，令路径搜索初始阶段有了一定的参考；建立了优先级规则，避免了多个无人机对同一区域的过度探索，加快了收敛速度。雷晓云［34］等基于DQN算法建立了一套奖惩机制，制定了在无障碍环境中设置随机起始点及目标点的智能系统训练方法，使得训练经验足够多样化、全面化，加强了该算法复杂环境中的局部路径规划适应能力，加快了算法收敛速度。

3.4 对比分析

局部路径规划算法的优缺点及改进方法如表2。

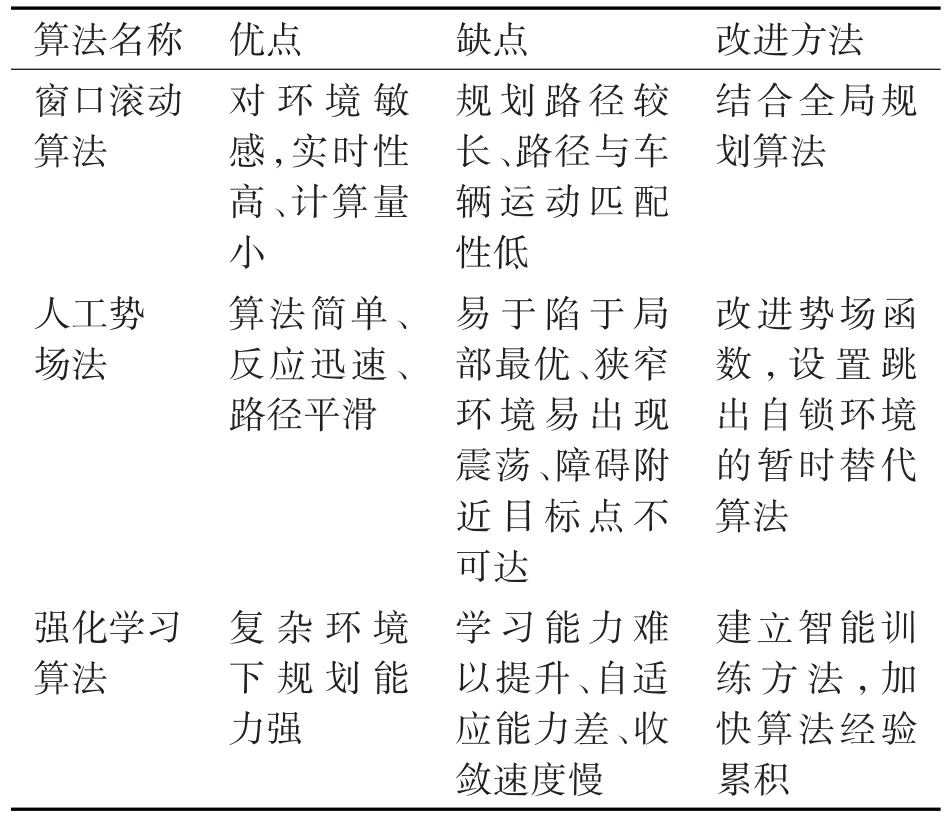
表2 局部路径规划算法的优缺点及改进方法

局部路径规划的对算法的反应速度要求较高，以至于算法的求解能力较弱或增强求解能力的途径较为困难。但是局部路径规划算法可看做一次次基于当前环境的全局路径规划，将全局路径规划算法同局部路径规划算法相结合，克服求解能力弱的缺点。

4 研究发展趋势

随着技术发展，人们对路径规划算法提出了更进一步的要求，希望有更迅速、更精确、自适应性更好的规划算法。面对实际情况中，复杂多变的环境，尤其是复杂的动态环境，现阶段算法的适应性较弱。因此，算法的发展呈现出以下趋势。

1）算法强化。各种算法都不可避免地有着一定的缺陷，诸如收敛速度慢，局部最优解等。研究学者们通过优化算法规则，提高算法收敛速度，提高路径规划最优解的精确度。简化算法模型，加快算法反应速度，提高算法实时性。例如遗传算法中加大优良遗传个体的复制概率，蚁群算法中非均匀初始信息素浓度分布以及随时间变化的信息素浓度挥发系数等。

2）算法融合。由于各个算法各有其独特优点，研究学者们更倾向于结合多种算法的优点，从而克服单个算法的固有缺陷，两者互补，全面提高算法效能。如粒子群算法与遗传算法结合，A*算法与蚁群算法结合等在试验验证中都有着远超单独某种算法的表现。但是算法融合导致算法建模复杂，执行响应慢，实时性低。在实际算法融合中应该考虑到一定的无人车辆行驶速度下，算法执行时间的长短对无人车辆精确位姿控制的影响。

3）自适应动态规划。人们逐渐不满足于已知环境下固定轨道的无人车辆的路径规划，而希望无人车面对未知环境自主选择路径，对动态障碍有自主避障响应的智能化算法。面对更为复杂多变，变量多，随机性高的外界环境，需要具有自我学习能力，事件启发性的强自适应性动态路径规划算法的支撑。

4）多样化环境下的避障策略。算法往往依托于环境，传统环境模型中，障碍主要分为固定障碍与动态障碍。但是无论是应用于城市交通普通无人车辆，还是野外探测的特种无人车辆，面对的障碍类型繁多。如城市交通中交通指挥，交通规则下的虚拟障碍，野外探测中面对前方草丛、浅坑、水坑、陡坡等可通过型障碍，非线性速度，难以预测轨迹的不确定性动态障碍等。因此，如何强化传感器识别，完善的环境模型，建立多样化的避障策略将成为新的方向。

5）规划参考代价多样化。传统路径规划算法一般以路程为参考代价，力求达到最短路径。但在实际过程中，最短路径有时并非最优路径。引入多样化的参考代价，例如文献［10］中以能量消耗为参考代价，取最小耗能为优。还可以根据耗时最短，相对最安全，最适于行驶等来进行路径规划。根据不同任务背景选取合适的参考代价规划路径对于无人驾驶有着重要的意义。

6）云端数据共享，算法自我学习进化。当前大数据时代，大量无人驾驶车辆在实际运行中积累了大量的数据，建立实时数据共享平台，对算法进行在线升级，通过强化学习的方式，对算法进行长期跟踪优化。

5 结语

该文章从全局路径规划，局部路径规划两个方面对遗传算法、蚁群算法、A*算法、粒子群算法、滚动窗口算法、人工势场算法、强化学习算法进行了基本原理以及当前研究现状的介绍，对无人车辆路径规划算法的发展趋势做了一定的总结，对无人驾驶车辆技术的发展方向有一定的借鉴参考作用。