基于粗糙集理论的装备质量基因要素信息筛选∗

战希臣 杨睿英 郭 聚

（海军航空大学航空基础学院 烟台 264001）

1 引言

装备是部队执行各项任务的基本物质保证，其质量情况与部队作战能力息息相关。影响装备质量的因素复杂多样，其中基因要素对装备质量特性的形成具有决定性作用。质量基因要素是指在装备全寿命周期中，对装备质量产生决定性作用且具有一定遗传特性的一系列关键指标［2］。在对装备质量进行跟踪管理的过程中，只要掌握了质量基因要素，也就掌握了装备的整体质量状况。所以，在影响装备质量的众多因素中筛选出质量基因要素，是非常重要的。比如在某型装备研制生产阶段，可根据该装备质量特性形成的过程和特点，归纳出装备质量的影响因素集，并以之构建质量指标体系。在此基础上，运用基于粗糙集属性约简的方法，可将该装备研制生产阶段的质量基因要素指标筛选出来。

2 某型装备质量指标体系构建

借鉴现代产品质量管理分析理论，从某型装备研制生产阶段的质量特性形成过程来看，其关键性影响因素为“5M1E”，即：人（Man）、机器设备（Ma⁃chine）、材料（Material）、测量（Measurement）、方法（Method）和环境（Environment）6 个方面［1］。结合“5M1E”理论与该装备实际研制生产的特点，其质量的影响因素可归纳为以下7个方面：人员因素、生产设备因素、产品原材料因素、技术工艺因素、环境因素、资金保障因素和质量信息管理因素。通过在某军工单位实地调研的情况，对以上质量因素进行细化研究，可得到质量指标因素的二级指标，从而构建较为完整的装备质量指标体系，如图1所示。

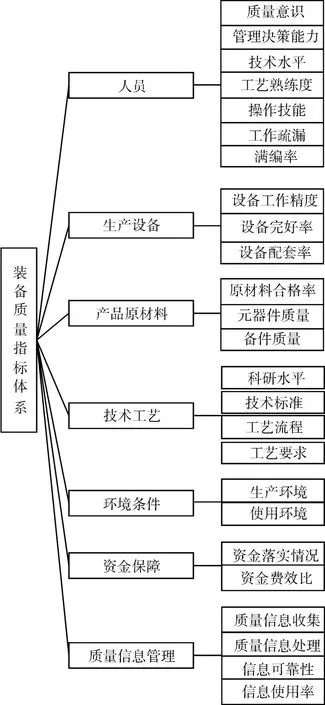
图1 装备研制生产阶段质量指标体系

3 基于粗糙集理论的装备质量基因要素信息筛选模型构建

3.1 粗糙集理论

1982年，波兰的Z.Pawlak教授在现有关系理论以及集合论的基础上，提出了粗糙集（Rough Set）的概念，用以处理难以精确计算以及不完整的数据。粗糙集以等价关系（不可分辨关系）将集合中的元素进行分类，并形成与其相对应的划分。同一划分被称为等价类，可用于信息的简化［5］。

粗糙集基于等价关系，通过构建信息表，利用可准确计算的近似集逼近待定的不精确集合。该集合的边界区域为上、下近似集之差。通过等价关系可以精确描述上、下近似集，而边界区域的模糊元素数目可以被计算出来。粗糙集理论的主要应用有两方面，一是对现有数据集合进行属性约简；二是分析分类规则［6］。本文主要是应用粗糙集属性约简的方法对装备质量基因要素指标进行筛选。下面介绍关于粗糙集的几个重要定义。

1）信息表

称四元组S=(U，A，V，f)为信息表（也叫决策表）。其中U={x1，x2，…，xn}为非空有限集合（xn为对象），称为论域；A为对象的属性集合，分为条件属性C和决策属性D，A=C∪D，C∩D=φ；V=∪Va是属性值的集合，Va表示属性a∈A的属性值值域；f:U×A→V是赋值函数，用于给所有对象的属性赋值，即a∈A，x∈U，fa(x)∈Va。

2）等价关系

对 于 ∀a∈R，R⊂A，x∈U，y∈U，如 果 有fa(x)=fa(y)成立，称对象x和y是对属性R的等价关系（也称不可分辨关系），也就是根据R中的属性无法区分对象x和y。表示为

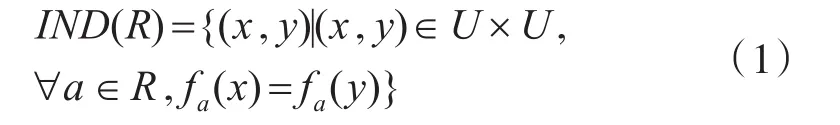
3）等价类与划分

在U中，具有同样的等价关系IND(R)的集合称为等价类，有：

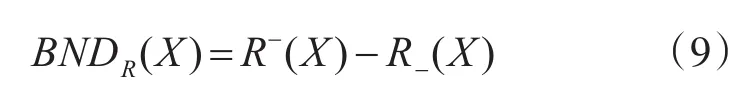
由此可知，正域POSR(X)为一定属于集合X的对象组成的集合；负域NEGR(X)为一定不属于集合X的对象组成的集合；边界域BNDR(X)表示不能确定是否属于集合X的对象组成的集合。

关于上近似、下近似、正域、负域、边界域的关系如图2所示。图中，椭圆区域表示集合X，红色区域为X的正域（下近似），灰色区域为X的负域，绿色区域为X的边界域，红色∪绿色区域为X的上近似。

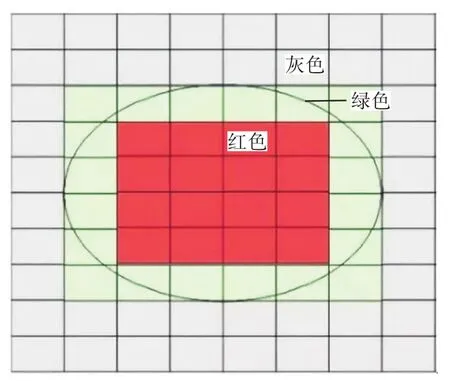
图2 近似集、正域、负域、边界域示意图

6）粗糙集

若R-(X)=R-(X)，即BNDR(X)=φ，称X为R的可定义集；若R-(X)≠R-(X)，即BNDR(X)≠φ，称X为R的粗糙集（也称不可定义集）。

R-(X)是包含X的最大R可定义集，R-(X)是包含X的最小R可定义集，若X为粗糙集，则X只能通过R-(X)与R-(X)近似地描述。

7）约简与核

信息表中的属性可能存在冗余属性，冗余属性对信息表的分类能力没有作用。属性约简也就是保持信息表分类能力不变的前提下，去除冗余属性。

对信息表S=(U，A，V，f)，如果B⊆A且有IND(B)=IND(A)，则B为A的一个约简，记为RED(A)。

属性集A的所有约简的交集称为A的核，记为

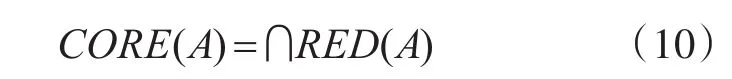
8）相对约简与相对核

设决策属性D的划分为U/D={E1，E2，…En}，则条件属性C相对于决策属性D的正域为

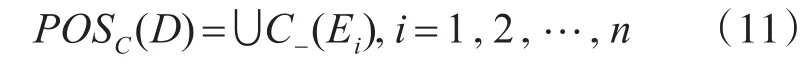
若c∈C，且POS（C-{c}）(D)=POSC(D) ，则 称c是C中不必要的，即可约简的；否则，称c是C中不可约简的。

若R⊆C，且R中所有元素都是必要的，如果有POSR(D)=POSC(D)，则称R是C中相对于D的约简，记为REDD(C)，所有这样的约简的交集称为C相对于D的核，记为

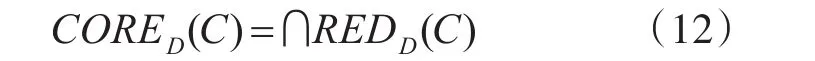
约简后的属性集称为属性约简集，信息表的属性约简集一般不唯一，约简集中属性个数最少的叫做最小约简集。属性约简问题一般都是求最小约简集，最小约简集不一定唯一，可根据问题实际进行选择。

3.2 筛选模型构建

基于粗糙集的指标信息筛选，也就是通过粗糙集理论的属性约简原理，通过约简得出属性集的最小约简集，从而在最大限度保留原始信息量的前提下，去除冗余指标，达到将指标体系化繁为简的目的，这也正是装备质量基因要素信息的本质要求，所以对于装备质量基因要素信息的筛选可以采用基于粗糙集的属性约简方法。

筛选模型的基本步骤如下。

Step 1指标体系初建。根据指标体系建立的一般原则，结合问题对象特点，通过调研，仔细分析问题的影响因素集（属性集），而后由大到小、由表及里地分层构建指标体系。

Step 2数据离散化。通过实地调研、采集历史数据或者专家打分等方法，收集指标的相应数据，并根据筛选模型的要求进行数据预处理。由于粗糙集方法不能处理连续属性问题，所以需要将数据离散化。定量指标一般为连续型数据，可采用等宽离散、等频离散或者聚类等方法离散化（具体方法见文献［6～8］）；对于定性指标，可采用专家打分法直接得到离散化数据。

Step 3建立信息表。根据指标性质，区分条件属性C和决策属性D；根据采集的数据样本份数确定论域U，而后构建信息表。

Step 4属性约简。通过粗糙集属性约简理论去除冗余属性（指标），得到最小约简集，从而得到筛选后的指标体系。

Step 5指标检验。采用KW检验、F统计量检验等方法检验筛选后的指标是否符合预定的数据相关性要求。若不符合要求，则调整指标体系，返回Step 1；若符合要求，则指标信息筛选完成。筛选模型的流程如图3所示。

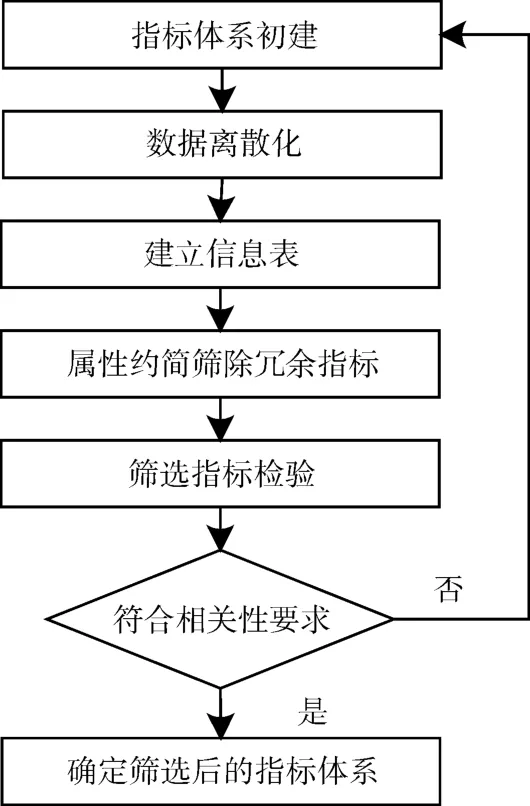
图3 指标信息筛选模型流程图

4 实例分析

对于某型装备研制生产阶段的质量基因要素信息筛选问题，根据图1中的质量指标体系展开信息筛选，该指标体系由7个一级指标和25个二级指标构成。质量基因要素指标属于一级指标，因此主要针对7个一级质量指标收集数据。

4.1 装备质量指标数据收集和信息表构建

为了准确收集某型装备研制生产阶段质量指标信息，采取在某军工单位实地调研以及邀请军工单位和部分院校专家进行专家打分的方式，采集7个指标的相关数据。鉴于粗糙集理论对于离散化数据的要求，将各项指标参数划分为4个等级，每个等级分别对应1～4分，如表1所示。通过专家打分得到每个指标对应的等级和分数，作为信息表的离散化数据。收集15组样本，并建立信息表，如表2所示。

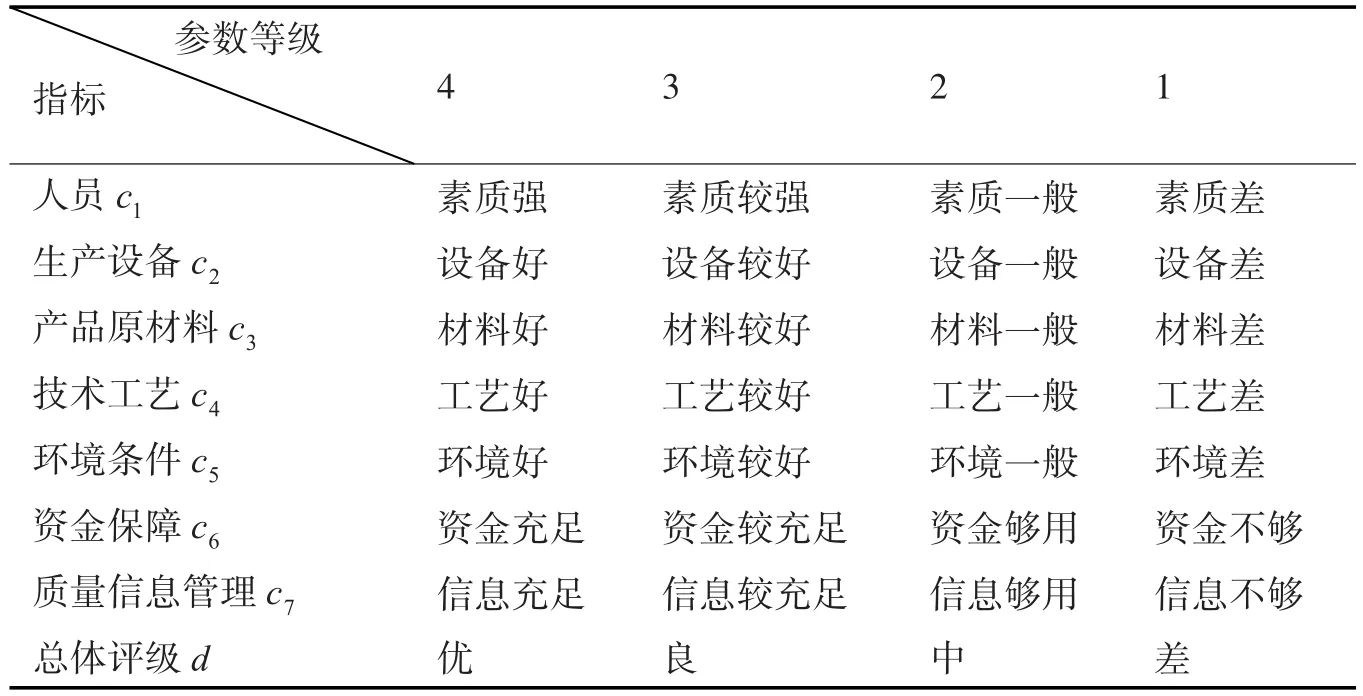
表1 指标参数等级表

4.2 装备质量基因要素指标筛选

1）由表2可直接得到论域U，条件属性C，决策属性D：

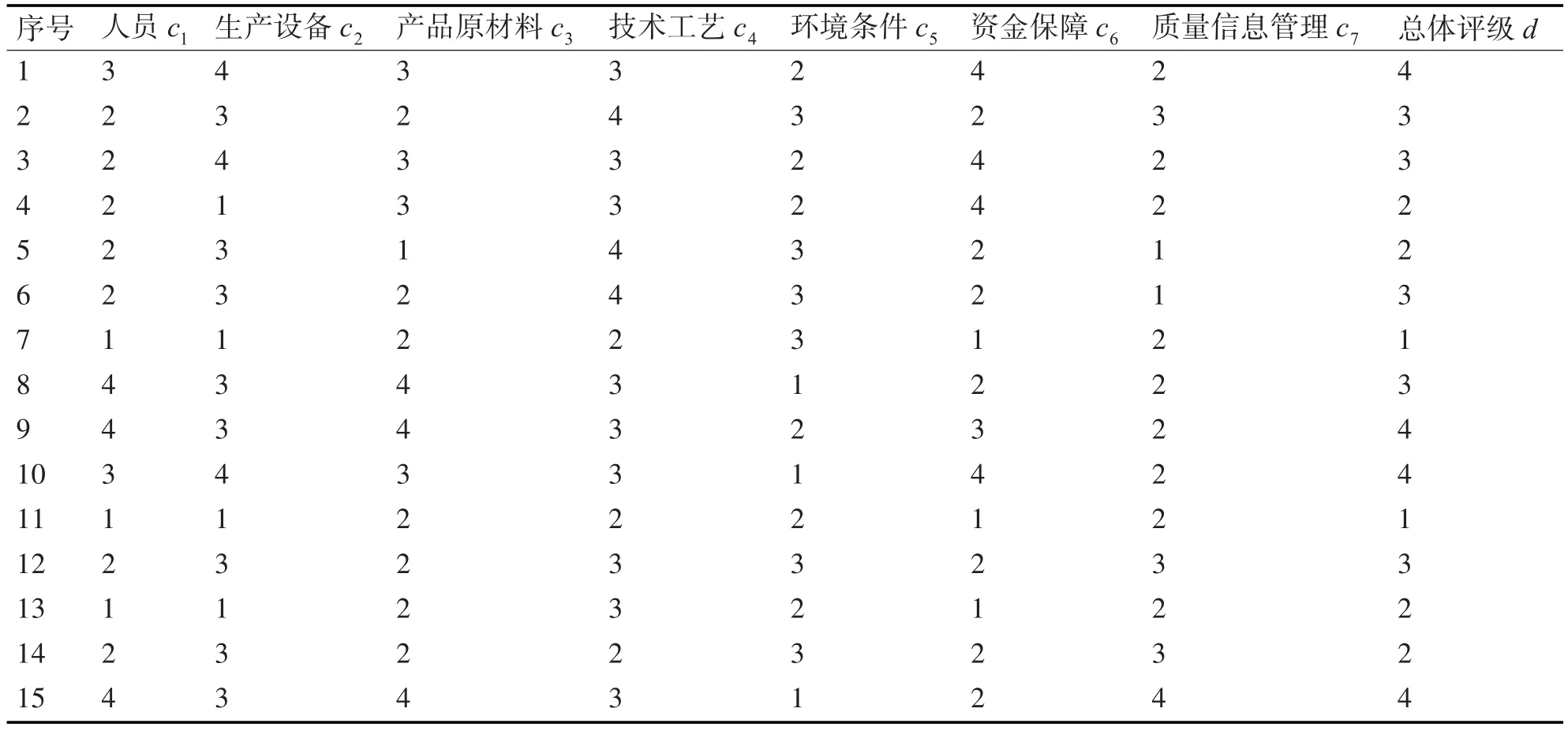
表2 装备质量指标信息表

4）根据以上计算，可知C的核CORED(C)={c1，c2，c3，c4，c7}，c5和c6是两个不必要属性，但不一定能同时约简。下面计算同时去除c5和c6时C相对于D的正域：

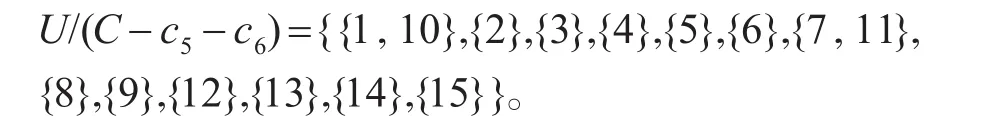
POS(C-c5-c6)(D)=POSC(D)，所以，c5和c6可以同时约简。

所以，C的最小约简为。经过属性约简，环境条件因素c5和资金保障因素c6被筛除。

4.3 筛选指标检验

指标筛选完成后，可采用KW检验法进行检验以验证筛选指标是否合理。

1）KW检验法

KW检验即Kruskal-Wallis检验，也称为H检验。KW检验是一种秩和检验，根据所有数据从小到大排列，算出每个数据的秩并计算每组数据的秩和，然后根据下式计算KW值：

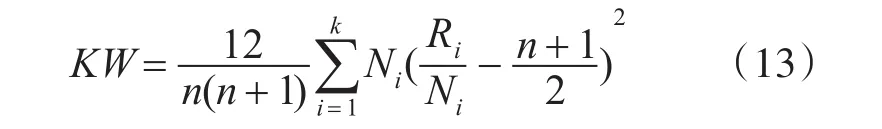
其中，Ni为每组的样本个数，Ri为每组的秩和。n为所有数据总数，k为组数。如果样本中存在结值（具有相同秩值的数据），则需要在KW值中加入校正系数C：

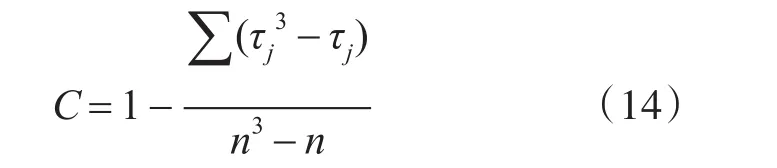
其中τj是第j个结值的个数。校正后的KW′值为

求出KW′值后，可通过查卡方检验表判断每组数据间是否具有显著性差异，从而验证筛选指标是否合理。

2）用SPSS软件进行筛选指标的KW检验

SPSS软件是IBM设计的一款数据分析与计算软件，具有实用高效便利的特点。本文使用SPSS Statistics 26版本进行筛选指标的KW检验。

在SPSS菜单栏“分析”中下拉菜单“非参数检验”、“旧对话框”、“K个相关样本”中打开KW检验功能。分别输入未筛选的7个指标数据和筛选后的5个指标数据，相关检验结果如图4、5所示。

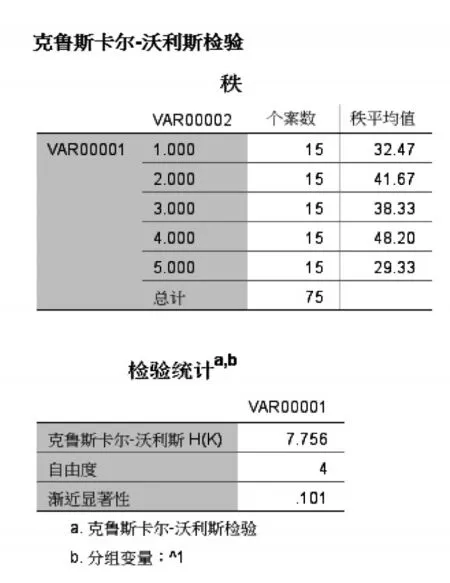
图4 筛选指标的KW检验结果

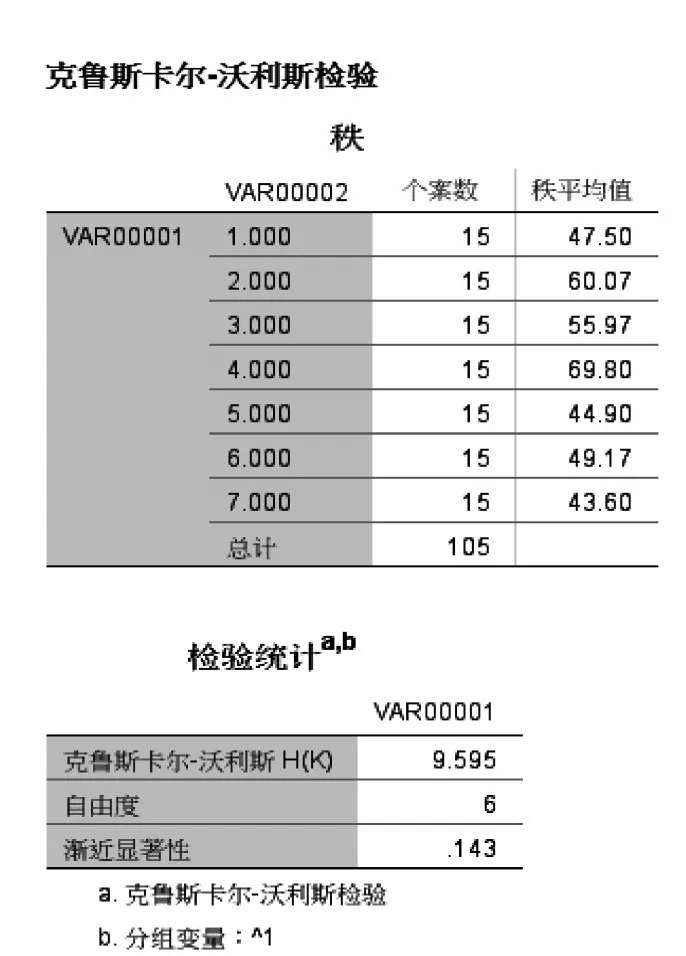
图5 原指标的KW检验结果

由图可知，筛选前7个指标的渐进显著性为0.143，筛选后5个指标的渐进显著性为0.101，筛选后的指标集的数据差异性变大了，说明数据的相对独立性更好，信息载荷量更大。因此，筛选的指标是合理的。至此，将原质量指标体系的7个质量指标成功简化为5个指标：人员因素、生产设备因素、产品原材料因素、技术工艺因素、质量信息管理因素，此即某型装备在研制生产阶段的质量基因要素。

5 结语

在现阶段装备质量管理中，要提高工作效率、更好地掌握装备质量动态情况，就势必要在繁冗复杂的质量指标因素中化繁为简、提取要素。装备质量基因要素信息筛选工作正是基于此思路展开的。本文构建的基于粗糙集理论的装备质量基因要素信息筛选模型，为装备质量信息的收集和提取提供了实用手段，并为后续的装备质量动态评估与跟踪管理以及装备质量信息系统的构建提供信息来源和数据支撑。