一种基于多模型量测转换的机动目标跟踪算法∗

刘 福马保东马 祥江 涛彭 瀚

（1.国网新源控股有限公司 北京 100964）（2.湖北白莲河抽水蓄能有限公司 武汉 438600）（3.昆明船舶设备研究试验中心 昆明 650000）

1 引言

目标跟踪技术一直是声呐技术研究中的焦点［1～5］。一般处理多目标跟踪的算法大多是以数据关联类的Bayesian理论为基础，往往存在计算量庞杂的缺点，基于随机有限集的多目标滤波算法具有处理实时性强、运算量低等优点，这使得此类多目标滤波器尤其受到重视［5～6］。由于水下目标的运动并非保持单一状态，随机出现的机动变化可能导致采用单模型算法的声呐系统不能稳定跟踪目标［7］，为了提高声呐系统的机动目标处理能力就需要设计多模型滤波算法处理状态的时变性。利用多目标量测更新状态时，存在空间转换的非线性关系，解决此类量测的非线性估计问题通常采用扩展卡尔曼滤波［6］、粒子滤波算法［7］以及基于量测转换的卡尔曼滤波方法［4］等。

Clark、Vo和Bell将GM-PHD滤波器［8-11］用于水下目标的检测和跟踪问题，系统采用主动前视声纳作为的传感器，搭载于自主水下航行器（AUV）上，AUV探测对象主要包括海洋生物及海床上的目标，由于AUV的运动性需考虑避碰及标记目的，即便相对于目标静止的海底也需要检测和跟踪。通过图像分割技术从声纳图像中提取高反射率区域作为感兴趣区域，提取区域质心作为特征馈入GM-PHD算法。通过仿真与AUV实测数据对比了GM-PHD与粒子PHD滤波器性能，前者性能更佳［12］。除了矩近似方式外，还有基于多伯努利滤波器的方法实现多目标跟踪［13］。本文主要研究的是概率假设密度算法的混合高斯实现方式，通过将GM-PHD方法与MM方法结合，并引入基于预测值的量测转换方法提出了一种新的多目标跟踪算法。经仿真验证，本文提出算法与单模型PHD算法相比跟踪精度更好、实时性更强。

2 问题建模

2.1 多目标量测模型

假设对于k时刻状态集Xk中任意目标状态在被检测的情况下，目标量测随机集Zk如式（1）所示。

2.2 GM-PHD基本假设

1）单个任意目标的Markov状态转移密度和量测是线性高斯模型，即

3 多模型GM-PHD算法

依据PHD方法的基本原理，在滤波过程中要对模型相关的高斯分量和无关高斯分量进行预测和更新。

3.1 预测过程

产生的新目标或分裂目标的预测，其强度函数按式（6）计算：

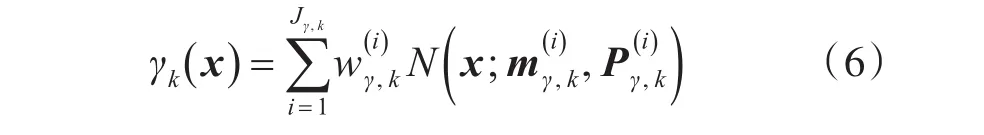
分裂产生的目标在k时刻的预测强度如式（7）～式（9）所示。

3.2 更新过程

目标漏检更新。漏检更新可分为两类：第一类是非时间连续目标的更新；第二类是有时间连续的更新，这类更新主要为对幸存目标的更新。对于Jk|k-1-Jk-1个非时间连续的高斯分量，给出第 j个分量的漏检更新如式（13）所示。

目标数和状态估计。抽取当高斯权超过特定阈值的分量，将其作为当前k时刻目标的估计结果。

3.3 算法流程总结

将本文提出的算法命名为MM-GM-PHDF算法，则算法的步骤可以总结为

1）初始化模型集合及初始高斯分量；

2）用式（6）～（9）计算新生、衍生高斯分量；

3）用式（10）～（12）计算幸存高斯分量；

4）用式（13）～（17）完成高斯分量漏检更新；

5）用式（19）～（20）计算预测误差统计矩；

6）用式（18）计算转换量测值；

7）用式（20）～（23）及式（26）计算量测更新后的高斯分量；

8）抽取权重满足阈值的高斯分量作为当前时刻目标状态估计，将抽取后的分量权值累积作为目标的个数估计；

9）重复步骤2）～8），估计出每次跟踪帧的目标状态和个数估计，每次量测更新后的高斯分量数会剧烈增涨［8］。因此，在每次迭代中需要对高斯分量个数控制，采用剪枝合并算法可有效防止分量暴增。若已知剪枝阈为τ，合并门限U，最大高斯分量数为Jmax。将高斯权低于τ的分布元素剔除获得新集合I，找出权重最大的高斯分量，挑选出满足合并条件的高斯分量，构成集合L。获得合并后的高斯分布，再从集合I中删除集合L中的元素，再次迭代，直到I=∅。

4 仿真实验

为了验证本文推导的基于多模型量测转换的机动目标跟踪算法（MM-GMPHDF）的效果，下面进行了计算机仿真，主要对比了CT-GMPHDF算法与CV-GMPHDF算法的跟踪精度与目标个数估计。

仿真条件为二维跟踪区域范围为200×200，机动目标个数为5，模型集合中包括匀速直线运动CV、常速率左转CTL和常速率右转CTR模型。目标存活概率为pS，k=0.95，过程噪声标准差分别在CV场景为0.01m/s2，CT场景中为0.10m/s2。假设新生目标的个数为3，权重为0.1。衍生目标个数为1，目标1起始于［40m，100m］位置处，整个1s～60s内目标1为CV运动。目标2在20s时出现在［100m，20m］处开始运动，在第80s消失，整个过程保持为CTR运动。目标3在30s时在［30m，140m］处出现，并在第100s时消失，30s～40s保持CV运动，40s～90s内保持CTR运动，在第90s转为CV。目标4在第40s从［100m，190m］处以CTR出发，持续了20s后转为CV运动，再持续20s后转为CTL运动。目标5是目标1的分裂体，于目标1运动10s后分裂，目标5在第50s时消失，整个过程中保持CTL运动。

图1给出了混合高斯分量的估计分布情况，可看到跟踪初期的高斯分量与目标起始点位置基本对应。采用OSPA距离［8］来对滤波器性能进行分析，OSPA距离可用于反映两个集合间元素的贴近程度，该距离大小可评估真实集与估计集间关系，从而反映了估计结果的准确性。仿真中，OSPA截断距离取c=7，阶数p=2。可以看出采用多模型的GMPHD方法的跟踪误差最低，其目标估计个数更接近真实值。

图1 高斯分量分布示意图

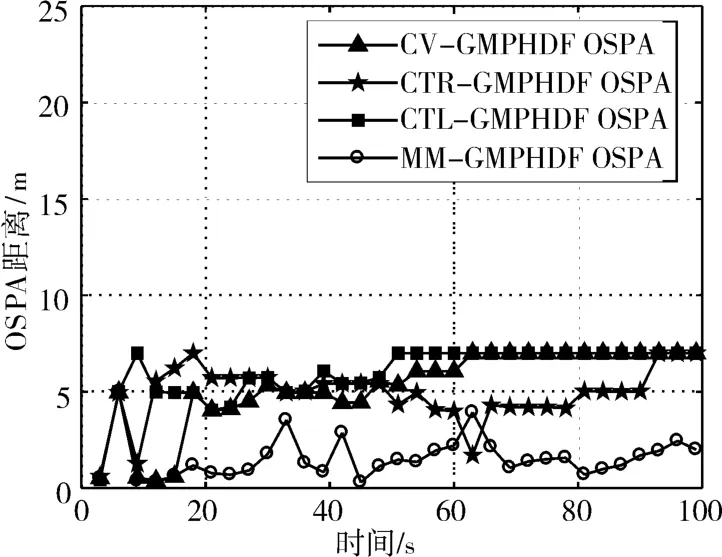
图2 OSPA距离变化对比

图3 目标数估计

5 结语

文章提出了一种基于多模型量测转换的GM-PHD算法，该算法能够在杂波环境下准确地对机动目标变化做出反应，相比单模型算法能够对机动目标精确地跟踪。同时对比了四种滤波算法的OSPA距离，符合较低跟踪目标集丢失率。相比单模型方法，在多模型下的PHD滤波能够保持良好的跟踪性能，可应用于实际杂波环境下的多目标探测与跟踪问题中。