基于改进的遗传算法的有刷直流电机PID参数整定
刘延飞,彭征,王艺辉,王忠
(火箭军工程大学 基础部,西安 710025)(∗通信作者电子邮箱bbmcu@126.com)
基于改进的遗传算法的有刷直流电机PID参数整定
刘延飞*,彭征,王艺辉,王忠
(火箭军工程大学 基础部,西安 710025)(∗通信作者电子邮箱bbmcu@126.com)
针对有刷直流(DC)电机的比例积分微分(PID)参数整定工作复杂耗时的问题,提出了一种基于改进型遗传算法(GA)的PID参数整定方法。首先,提出了适应度增强淘汰法则,改进了传统GA的选择过程;然后,提出了基因感染交叉方法,保证了进化过程中平均适应度值的增加;最后,删除了传统GA中不必要的复制操作,提升了算法的运行速度。通过电机传递函数进行建模和仿真分析。实验结果表明,与常规整定方法相比,所提改进型GA能够显著提升PID参数整定效果,且改进型GA相较于传统GA,达到同样进化效果所需的进化代数减少了79%,算法运行速度提升了4.1%。所提出的改进型GA从选择和交叉两个关键操作步骤对GA进行了改进,并应用于PID参数整定使得上升时间更少、稳定时间更短、过冲更小。
比例积分微分参数整定;遗传算法;基因感染交叉;适应度函数;传递函数建模
0 引言
有刷直流(Direct-Current, DC)电机因成本低、易于控制等特点在工业控制中得到了广泛的应用[1-3],作为有刷直流电机最为常用的控制器之一的比例积分微分(Proportion Integral Differential, PID)控制器由于结构简单,安全性和鲁棒性高,已在其他许多实际控制中得到应用[4-6]。随着工业的不断发展,现在已采用PID控制器来控制具有精确数学模型的特定系统的系统输出[7-8],由此带来的PID参数整定问题也愈发受到人们的重视。常规PID参数整定方法有ZN (Ziegler-Nichols)[9-11]、CC(Cohen-Coon)方法[12-13]、内部模型控制(Internal Model Control, IMC)[14-16]以及衰减曲线法(Attenuation Curve, AC)[17-18]。这些方法都比较成熟且在工业中得到了广泛的应用。随着具有非线性行为、高阶和长响应时间的工业系统复杂性的提升,进一步增加了PID参数设置的困难[19]。因此,以遗传算法(Genetic Algorithm, GA)为代表的智能PID参数整定方法得到了不断的发展,提高了PID参数整定的效率,扩大了PID的应用途径。
遗传算法是参数优化的有力工具[20-22],但存在容易过早收敛、计算精度无法定量分析、相较于传统优化算法计算效率较低等问题,如何解决这些问题进而推动其在工业领域的应用成为研究人员关注的重点。文献[23]中以时间积分乘以绝对误差(Integral of Time multiplied by Absolute Error,ITAE)为目标函数,使用GA整定PID参数,与ZN、IMC和未修改适应度函数的GA相比,修改适应度函数后的GA获得了更少的上升时间、稳定时间和更小的过冲;文献[24]中对核电站负载跟随的PID参数使用了实编码遗传算法进行优化和调度,提出的控制系统可在很长的时间内跟踪需求功率水平的变化;文献[25]中提出了使用遗传算法调整电液伺服系统PID控制器参数,实验发现遗传算法优化的PID控制器提供了比ZN自动调整方法和粒子群优化(Particle Swarm Optimization, PSO)更好的闭环;文献[26]中提出了一种基于改进比例选择算子、自适应交叉概率和自适应变异概率的优化遗传算法,研制了一种基于质量流量控制器的混合气系统,并设计了一种基于PID的遗传算法优化控制系统,克服了常规混合气系统精度差、建立时间长的缺点。
为了提高遗传算法在有刷直流电机PID参数整定中的计算效率,本文提出了一种增强感染遗传算法(Enhanced Infection Genetic Algorithm, EIGA),通过改进交叉操作和适应度函数计算方法,提升了参数优化能力,并通过删除复制操作降低了算法复杂度,在保持遗传算法较好的参数寻优能力的情况下耗费较低的计算成本。通过仿真实验对改进型遗传算法与常规算法的PID参数整定效果进行了对比,实验结果表明,所提EIGA在保证控制器性能的同时提高了计算效率,有利于推动遗传算法在工业领域的应用。
1 系统基本原理
1.1 PID控制器
PID控制器是业界内最普遍采用的控制器(约占控制器的90%)。PID控制器由3个基本增益参数组成,其结构如图1所示。
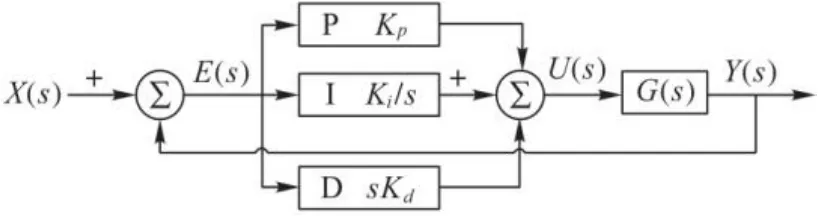
图1 PID控制器Fig. 1 PID controller
其拉普拉斯形式为:
则传递函数为:
1.2 常规遗传算法
遗传算法是在模拟生物遗传学与自然选择机理的基础上,人工构造的一种搜索最优解的方法。在遗传算法中,解决方案的集合被称为种群,种群中的每个解决方案被称为个体,解决方案的解决效果被称为表现型,解决方案效果的评价指标被称为适应度值。
利用遗传算法进行最优解搜索的流程如图2所示,其具体步骤如下。

图2 遗传算法流程Fig. 2 Flow chart of genetic algorithm
步骤1 编码。编码是指将解决方案的数据表示成遗传空间的基因型串数据结构,这是将实际问题抽象成数学问题的第一步,也是利用遗传算法解决问题的基础。编码的长度直接影响计算结果的精度与算法的计算效率,在实际问题处理时,常采用二进制编码,一般依据结果精度的要求确定编码的长度。
步骤3 适应度评估。适应度评估是指通过构造适应度函数评价解决方案的适应度值,适应度值越高代表方案的解决效果越好;反之,解决效果越差。这是利用遗传算法求解的关键,适应度函数的选取影响后续的计算过程与算法的收敛性。
步骤4 选择。选择的目的是为了从当前种群中选出优良的个体,作为父代繁殖下一代,选择体现了达尔文的优胜劣汰、适者生存原则。通常根据适应度值的大小,利用赌轮选择或者联赛选择方法进行选择,选择对于算法的收敛性同样有重要影响。
步骤5 交叉。交叉是最主要的遗传操作,模仿自然界的交配过程,通过交叉组合父辈个体的特性。交叉保证了种群的稳定性,并朝着最优解的方向进化。常用的交叉方法有一点交叉和两点交叉。交叉率直接影响算法收敛性,交叉率过低时,容易陷入局部最优解;交叉率过高时,算法收敛时间变长,算法复杂度极大增加。
步骤6 变异。变异是对选中的个体以一定的概率随机地改变串数据结构中的某个串的值,同生物界一样,其发生的概率很低。变异保证了种群的多样性,避免交叉可能产生的局部收敛。
完成步骤6之后,重复步骤3~6,进行最优解搜索,通过遗传代数或者误差控制算法的进程。
1.3 直流电机建模
对电机的PID控制强烈依赖于电机自身的参数,电机厂商往往会给出这些参数,使得研究人员能够计算出电机的传递函数,然而一些电机厂商所给的参数存在着一定的误差,这样的误差也使得电机的PID参数不能很好地适用于不同系统中的电机。实际应用中,往往需要对电机的参数进行测定并重新计算传递函数。常规电机参数测定方法是使用通用仪器测量电机的各个参数,然后进行计算得到传递函数。而本文采用了参数辨识方法,该方法需要测量电机的阶跃响应曲线,然后通过参数估计得到电机参数,最后计算得到电机传递函数。电机参数估计如图3所示,具体辨识过程如下。
步骤1 测量实物电机阶跃响应,将该响应绘制成曲线,该曲线用于对比仿真估计的电机参数与实物电机的阶跃响应误差。
步骤2 向仿真电机系统输入阶跃激励信号,测量仿真电机的阶跃响应,并与实物电机阶跃响应曲线进行对比,得到仿真电机系统与实物电机的误差。
步骤3 程序根据误差自动调整仿真电机参数,使得仿真电机阶跃响应与实物阶跃响应误差最小。当调整结束时,得到与实物电机误差最小的仿真电机参数。
最后使用得到的参数计算出电机传递函数。该方法能够快速且准确地计算出电机的参数,减少构建电机模型的时间,使得能够将更多的时间用在算法的改进上。

图3 电机参数估计Fig. 3 Motor parameter estimation
2 增强感染遗传算法
遗传算法中,种群后期相似基因的竞争关系与收敛精度密切相关;算法的收敛速度很大程度上取决于对适应度值较差的个体的淘汰速度。针对上述性能分析,本文对遗传算法进行改进,提出了增强感染遗传算法。
2.1 增强淘汰法则
常规遗传算法在进化后期,个体之间适应度值差异小,选择过程竞争较弱,致使种群进化停滞,寻优精度不高,收敛速度较慢。本文在得到个体的适应度值后,首先计算种群平均适应度,然后比较个体与种群的平均适应度,当个体适应度低于种群平均适应度时令该个体适应度值为0。该操作使得在种群进化初期能够快速淘汰较多适应度低的个体;淘汰标准随着代数增加而变化,在进化后期,能够增强相似个体之间的竞争,防止种群进化停滞。

图4 函数曲线Fig. 4 Curves for function
2.2 基因感染交叉方法
常规遗传算法采用交叉和变异进行随机搜索。当两个个体的染色体进行交叉操作产生新个体时,这种方式在父辈个体适应度值较大时容易产生适应度值较低的子代个体,从而使种群平均适应度降低,背离最优解。而基因感染交叉通过将父辈的大部分基因感染替换适应度值低的个体基因,有效防止了新个体适应度值的降低。如图5所示,基因感染交叉方法的描述如下。
步骤1 使用增强淘汰法则重新计算个体的适应度值,使得在进行选择操作时适应度较低的个体不会被选择。
步骤2 对经过选择之后的种群中每一个个体进行如下操作:根据比例选择原则选取一父辈,并将该个体的适应度与父辈适应度进行比较。当该个体适应度小于父辈适应度时,在父辈染色体中选取低位的一点,使用这点之前的高位基因感染替换个体染色体中对应的基因段。当该个体适应度大于等于父辈时,不再进行基因感染交叉操作。

图5 基因感染交叉操作Fig. 5 Gene infection crossover operation
在线性问题中,当父辈将大部分高位基因感染替换个体基因时,个体的表现型将迅速靠近父辈,防止产生适应度值较低的个体,从而防止降低种群平均适应度值。由于保留了自身低位基因,个体保留了一定的搜索能力,能够在父辈的表现型附近进行搜索,增大了搜索到最优解的概率;而在非线性问题中,单纯以父辈表现型为基础的搜索容易导致出现局部最优解,因此在执行基因交叉感染时,对每一个个体都运用比例选择原则选择父辈,保证父辈表现型能够被充分选择、比较,既保证了搜索速度,又保留了父辈表现型的多样性,防止出现局部最优解。
2.3 EIGA基本流程
如图6所示,增强感染遗传算法(EIGA)的流程如下。
步骤1 算法首先设置交叉率、变异率等参数,并初始化种群。初始化种群,即在选择好编码方式的基础上,根据选择的种群大小,生成一个完成了个体编码的编码集合,作为算法运行的初始值,常用的编码方式有二进制编码、格雷码编码。
步骤2 根据新的适应度函数计算法则计算各个个体的适应度值,并计算选择操作需要的数列,即以原适应度函数为基础计算适应度值,然后通过增强感染法则更新种群中个体的适应度值。
步骤3 判断是否满足停止进化的条件,当满足停止进化的条件时,退出程序并给出结果,否则进行下一步。常用的算法控制条件有进化代数、迭代误差等。
步骤4 进行基因感染交叉操作,然后进行变异操作,转至步骤2。运用比例选择原则对种群个体进行交叉操作,在确保计算精度的同时提升进化速度。

图6 增强感染遗传算法流程Fig. 6 Flow chart of enhanced infection genetic algorithm
与常规遗传算法相比,增强感染遗传算法主要在两个方面进行了改进:一是得到每个个体的适应度值后,根据增强淘汰法则重新计算适应度值,增强了不同基因的竞争,在进化前期增大了适应度值小的个体的淘汰力度,加快了收敛,在进化后期增大了相似染色体的竞争,提高了收敛精度;二是通过改进基因感染交叉方法保证后代个体的适应度值高于父代,避免产生适应度值较低的个体,防止了种群平均适应度值的降低。
3 基于EIGA的PID参数整定
图7给出了将改进的遗传算法应用于电机PID参数整定的系统结构,其中,为电机的速度传递函数。输出速度反馈到输入,并与设定速度进行比较,生成误差信号;然后,将该信号送给PID控制器,PID控制器调整输出使得最小。另一方面,EIGA使用误差信号的绝对误差积分(Integral Absolute Error, IAE)来形成目标函数:
对于该目标函数,误差越小函数值越小,选择操作的原则是选择适应度值较高的个体,因此该函数并不适宜作为适应度函数。将该函数求倒数,得到适应度函数:
电机PID参数整定系统的总体方案描述如下。
步骤1 在遗传算法的种群中选择一个个体,进行解码得到表现型(,,)。使用该参数初始化PID控制器,向系统输入阶跃信号,测量系统的输出响应,并将其保存下来。使用系统的误差信号计算IAE,并计算适应度值。
步骤2 对种群中所有个体进行步骤1的操作,得到各个个体的适应度值。通过增强感染遗传算法产生新的个体,并进行参数取值范围内的全局搜索,搜索适应度值更高的解决方案。在评估所有个体的适应度值后,记录下适应度最高的个体染色体。
步骤3 判断进化代数或者误差是否达到设置的数值,当达到进化停止条件时,对所有代的最高适应度进行排序,得到整个进化过程中适应度最高的个体,并对该个体的基因解码得到表现型(,,)。

图7 基于EIGA的PID控制器Fig. 7 PID controller based on EIGA
4 仿真与结果分析
4.1 电机传递函数仿真
使用实物电机进行实验不仅耗时还会缩短电机寿命,数值仿真是有效解决这一问题的方法,在进行仿真前需要对电机进行建模。通过建模仿真得到的电机参数如表1所示。

表1 直流电机的参数Tab. 1 Parameters of DC motor
电机速度传递函数为:
4.2 多种PID参数整定方法仿真
为了检验EIGA的PID参数整定效果,在相同的电机模型基础上,对不同整定方法的整定效果进行了仿真。同时,为了更好地对比EIGA与GA的性能差异,将两种算法的参数设为相同值,因为GA参数设置没有确定的选取方法,所以根据增大种群数量会提高计算精度、增加计算成本,增大交叉率、变异率会减慢收敛速度等规律,以及为了保证有刷直流电机性能,设置参数如表2,且令EIGA的值为1。这样可以将种群数量设置在一个较低的水平,以模拟较低计算能力下的算法运行环境,更好对比两种遗传算法的性能差异。

表2 GA 和 EIGA的参数Tab. 2 Parameters of GA and EIGA
仿真中使用常规整定方法、GA和EIGA对PID控制器参数进行整定,并使用整定的参数初始化PID控制器,仿真得到系统的阶跃响应。使用各方法对应的阶跃响应如图8所示。由图8可以很容易地看出:常规方法中IMC方法的稳定时间最长,但是其过冲较小;ZN方法的过冲最小;AC方法产生的过冲最大,但稳定时间相较ZN、CC、IMC方法更短;而GA、EIGA在上升时间、过冲和稳定时间方面的性能都明显优于常规整定方法。

图8 不同方法的阶跃响应Fig. 8 Step response of different methods
从图8中难以看出GA与EIGA的差别,所以将两者阶跃响应进行单独比较,结果如图9所示。由图9可以看出,EIGA整定方法产生的PID参数阶跃响应相较于GA整定方法,上升速度更快,稳定时间更短。

图9 GA与EIGA的阶跃响应Fig. 9 Step response of GA and EIGA
使用各方法整定的PID参数的阶跃响应部分性能指标差异较小,为更精确比较各方法的优劣,表3给出了不同方法下的阶跃响应性能指标。表4给出了各整定方法得到的PID参数。可以看出,GA和EIGA整定方法产生的值明显大于常规整定方法,这极大缩短了系统阶跃响应的上升时间,而较大的值抑制了较大过冲的产生,较大的值使得系统快速接近稳态。

表3 不同方法下的系统响应性能Tab. 3 System response performance under different methods

表4 不同方法整定的PID参数Tab. 4 PID parameters tuned by different methods
为进一步分析EIGA和GA的整定效果,本文统计了两种算法中每一代种群的平均适应度值,结果如图10所示。由图10可以得到以下结论:1)EIGA的平均适应度值上升较快,这是由于适应度增强淘汰法则能够快速淘汰适应度值较低的个体,快速提高种群的平均适应度。2)相较于GA,EIGA较少出现平均适应度值下降,这表明了基因感染交叉方法相较于常规交叉方法能够更加有效地防止适应度的降低。仿真实验中,还测算了两种算法的时间,GA所用的时间为EIGA的1.042 8倍,这也表明了减少复制操作有效降低了算法时间复杂度。
分析: 形态学上端即形态学顶端,是指生长延伸的部位;形态学下端是指形态学基端。在地上部分生长素主要从形态学顶端向形态学基端运输,而地下部分则主要从形态学基端向形态学顶端运输。根尖产生的生长素含量很少,根所需的生长素主要来自地面以上部分向下的传递。地上部分产生的生长素通过中柱越过根茎交界处进行向顶式运输,然后根尖的生长素再经根的表层细胞通过向基式运输向上回流(图2)[8]。
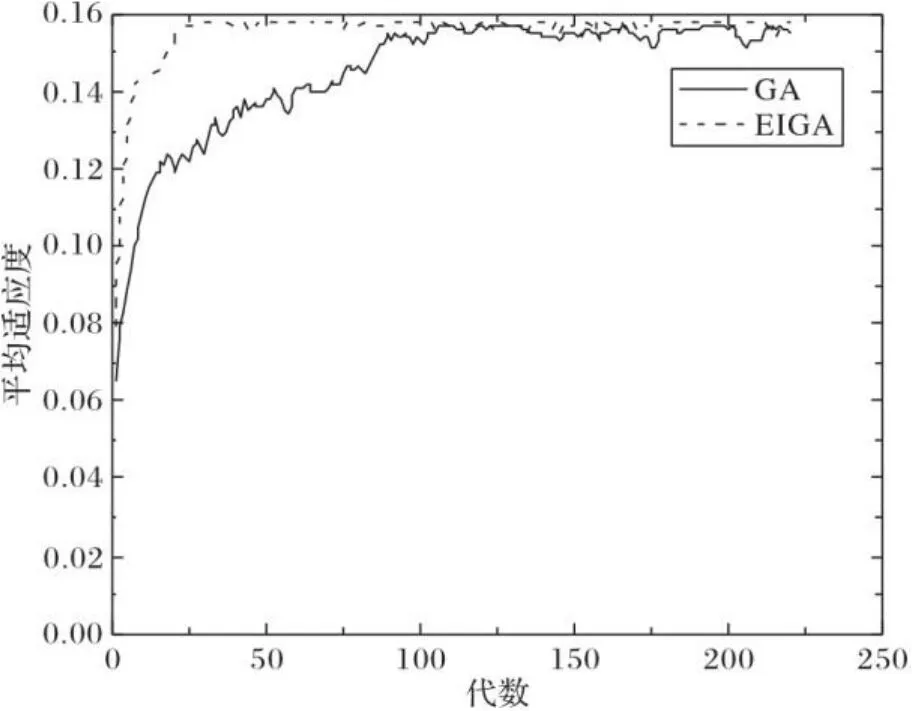
图10 GA与EIGA的个体平均适应度Fig. 10 Individual average fitness of GA and EIGA
上述结果表明,所提出的改进方法使得EIGA在耗费相近的计算成本下,拥有更好的全局寻优能力。进一步对比两种算法的优化效果,取得两种方法所优化出的最高适应度值,并测量两种方法到达该最高适应度值的60%、90%、95%、99%、100%所用的进化代数,结果如表5所示。表5中,EIGA所用代数明显少于GA,在实现同等优化效果时,EIGA可以有效降低参数优化所需的计算成本。

表5 对应适应度值的进化代数Tab. 5 Generation number corresponding to fitness value
5 实验验证
在进行数值仿真前,需要首先测量电机阶跃响应曲线,而在实物验证中,需要使用整定的参数初始化系统PID控制器,并通过系统阶跃响应曲线判断参数的实际适用性,为此搭建了如图11所示的系统。系统中包括电脑上位机程序和电机控制系统。在电机控制系统中,1 GB的SD卡用于记录程序运行过程中产生的数据,H桥式驱动板根据控制板送出的电机驱动信号控制电机,1024线编码器通过齿轮啮合连接电机,测量电机转速。控制板处理器采用了STM32H743芯片,主要运行PID电机控制程序,该程序通过编码器脉冲测量电机转速,并将转速等信息经由USB晶体管-晶体管逻辑电平(Transistor-Transistor Logic, TTL)模块发送至电脑上位机程序。

图11 直流电机控制系统Fig. 11 DC motor control system
在第4章中得到了各类方法整定的PID参数,使用这些参数初始化实物电机系统的PID控制器进行实验验证,实验中将目标速度设为60 r/s。图12给出了实验中得到的不同参数下的系统阶跃响应曲线。
可以从图12得到以下结论:1)对于上升时间,EIGA的上升时间最短,GA和AC方法次之,ZN和IMC方法上升时间最长;2)对于稳定时间,AC和CC方法的稳定时间最短,EIGA和GA次之,ZN和IMC方法的稳定时间最长;3)对于过冲,AC方法的过冲最大,其他方法无明显过冲。
实验和仿真的结果都表明,EIGA和GA在PID参数整定效果上表现出相近的特性,且整体效果优于常规整定方法,验证了遗传算法具有良好的参数寻优能力,同时仿真结果表明,EIGA相较于GA降低了算法的时间复杂度,提升了算法的收敛速度,提高了最优解的精度。但是,由于仿真系统与实验系统之间存在误差,两者的结果在总体吻合的基础上存在一定的偏差;而且实验系统的参数测量精度受到限制,导致系统的上升时间、稳定时间和过冲难以测量。

图12 不同方法的系统阶跃响应Fig. 12 System step response of different methods
6 结语
本文提出了一种改进的遗传算法,并利用该算法对有刷直流电机的PID参数进行整定。仿真与实验结果表明,遗传算法具有强于常规整定方法的参数寻优能力,而且改进型遗传算法比传统遗传算法收敛速度更快,寻优精度更高,验证了改进方法的有效性与可靠性。但是,由于实验条件的限制,实验效果与仿真结果还存在偏差,需要通过改进实验条件优化实验结果,缩小仿真与实验的误差。尽管改进效果较为明显,但本文所提出的算法仍存在面向对象单一、整定过程相对繁琐的局限性,接下来将进一步研究自动化程度更高、使用范围更广的PID参数整定方法。
[1] YAN W B, WANG D D, JIA P F, et al. The PWM speed regulation of DC motor based on intelligent control [J]. Systems Engineering Procedia, 2012, 3: 259-267.
[2] DIMEAS I, PETRAS I, PSYCHALINOS C. New analog implementation technique for fractional-order controller: a DC motor control [J]. AEU — International Journal of Electronics and Communications, 2017, 78: 192-200.
[4] 赵天才,余洪锋,郝向泽,等.基于PID算法的水稻直播机播量控制系统的设计与试验[J].华南农业大学学报,2019,40(2):118-125.(ZHAO T C, YU H F, HAO X Z, et al. Design and experiment of sowing control system for rice direct seeder based on PID algorithm [J]. Journal of South China Agricultural University, 2019, 40(2):118-125 .)
[5] 吕东阳,王显军.基于模糊PID控制的电机转台伺服系统[J].计算机应用,2014,34(S1):166-168,185.(LYU D Y, WANG X J. Servo motor system based on fuzzy PID control [J]. Journal of Computer Applications, 2014, 34(S1):166-168, 185.)
[6] 黄玉钏,曲道奎,徐方,等.伺服电机的预测控制与比例-积分-微分控制[J].计算机应用,2012,32(10):2944-2947.(HUANG Y C, QU D K, XU F, et al. Model predictive control and PID control on servo motor [J]. Journal of Computer Applications, 2012, 32(10): 2944-2947.)
[7] CIVELEK Z, LÜY M, ÇAM E, et al. Control of pitch angle of wind turbine by fuzzy PID controller [J]. Intelligent Automation and Soft Computing,2016, 22(3): 463-471.
[8] MAMUR H. Design,application, and power performance analyses of a micro wind turbine [J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2015, 23(6): 1619-1637.
[9] 于国强,刘克天,胡尊民,等.基于Ziegler-Nichols优化算法的火电机组负荷频率PID控制研究[J].热力发电,2021,50(9):137-144.(YU G Q, LIU K T, HU Z M, et al. PID control of load frequency of thermal power unit based on Ziegler-Nichols optimization algorithm [J]. Thermal Power Generation, 2021, 50(9): 137-144.)
[10] BRITO A G. On the misunderstanding of the Ziegler-Nicholsʼs formulae usage [J]. IEEE/CAA Journal of Automatica Sinica, 2019, 6(1): 142-147.
[11] FIŠER J, ZÍTEK P. PID controller tuning via dominant pole placement in comparison with Ziegler-Nichols tuning [J]. IFAC-PapersOnLine, 2019, 52(18): 43-48.
[12] ISDARYANI F, FERIYONIKA F, FERDIANSYAH R. Comparison of Ziegler-Nichols and Cohen Coon tuning method for magnetic levitation control system [J]. Journal of Physics: Conference Series, 2020, 1450: Article No.012033.
[13] GAMASU R, JASTI V R B. Robust Cohen-Coon PID controller for flexibility of double link manipulator [J]. International Journal of Control and Automation, 2014, 7(1): 357-368.
[14] 盛锴,邱靖,周刚,等.基于IMC-PID的超临界火电机组AGC性能优化[J/OL].控制工程.(2021-01-18)[2021-09-09].https://doi.org/10.14107/j.cnki.kzgc.20200452. (SHENG K,QIU J, ZHOU G, et al. Performance optimization of supercritical thermal power unit’s automatic generation control based on IMC-PID [J/OL]. Control Engineering of China. (2021-01-18) [2021-09-09]. https://doi.org/10.14107/j.cnki.kzgc.20200452.)
[15] SHAMSUZZOHA M. IMC based robust PID controller tuning for disturbance rejection [J]. Journal of Central South University, 2016, 23(3): 581-597.
[16] BEGUM K G, RAO A S, RADHAKRISHNAN T K. Enhanced IMC based PID controller design for Non-Minimum Phase (NMP)integrating processes with time delays [J]. ISA Transactions, 2017, 68: 223-234.
[17] WANG W B, LIU D Y, YAO Y Q. Study of PID control algorithm based on the critical ratio method [J]. Applied Mechanics and Materials, 2014, 494/495: 1246-1248.
[18] XIA C G, CAO C. Tuning of PID parameters and fuzzy adaptive PID control of the hydrostatic driving system [J]. Advanced Materials Research, 2012,403/404/405/406/407/408: 5112-5116.
[19] ANG K H, CHONG G, LI Y. PID control system analysis, design, and technology [J]. IEEE Transactions on Control Systems Technology, 2005, 13(4): 559-576.
[20] 黄书召,田军委,乔路,等.基于改进遗传算法的无人机路径规划[J].计算机应用,2021,41(2):390-397.(HUANG S Z, TIAN J W,QIAO L, et al. Unmanned aerial vehicle path planning based on improved genetic algorithm [J]. Journal of Computer Applications, 2021, 41(2):390-397.)
[21] ZHONG S S, XIE X L, LIN L, et al. Genetic algorithm optimized double-reservoir echo state network for multi-regime time series prediction [J]. Neurocomputing,2017, 238: 191-204.
[22] MOHAMAD E T, FARADONBEH R S, ARMAGHANI D J, et al. An optimized ANN model based on genetic algorithm for predicting ripping production [J]. Neural Computing and Applications, 2017, 28(S1): 393-406.
[23] ZAHIR A A M, ALHADY S S N, OTHMAN W, et al. Genetic algorithm optimization of PID controller for brushed DC motor [M]// HASSAN M H A. Intelligent Manufacturing amp; Mechatronics, LNME. Singapore: Springer, 2018: 427-437.
[24] MOUSAKAZEMI S M H,AYOOBIAN N, ANSARIFAR G R. Control of the reactor core power in PWR using optimized PID controller with the real-coded GA [J]. Annals of Nuclear Energy, 2018, 118: 107-121.
[25] SAMAKWONG T,ASSAWINCHAICHOTE W. PID controller design for electro-hydraulic servo valve system with genetic algorithm [J]. Procedia Computer Science, 2016, 86: 91-94.
[26] WANG C C, CHEN F, ZHANG G, et al. Design of genetic algorithm optimized PID controller for gas mixture system [C]// Proceedings of the 2017 13th IEEE International Conference on Electronic Measurement and Instruments. Piscataway:IEEE, 2017: 6-9.
PID parameter tuning of brushed direct-current motor based on improved genetic algorithm
LIU Yanfei*, PENG Zheng,WANG Yihui, WANG Zhong
(Department of Basic Sciences,Rocket Force University of Engineering,Xi’an Shaanxi710025,China)
Aiming at the complicated and time-consuming problems of brushed Direct-Current (DC) motor Proportion Integral Differential (PID) parameter tuning, a PID parameter tuning method based on improved Genetic Algorithm (GA) was proposed. Firstly, a fitness enhanced elimination through selection rule was proposed, which improved the selection process of traditional GA. Then,a gene infection crossover method was proposed to ensure the increase of the average fitness value in the evolution process. Finally, the unnecessary copy operation in traditional GA was deleted to improve the running speed of the algorithm. Modeling and simulation analysis were carried out through the motor transfer function. Experimental results show that, compared with conventional tuning methods, the proposed improved GA can significantly improve the PID parameter tuning effect. At the same time, compared with the traditional GA, the improved GA reduces the evolutionary generation number required to achieve the same evolutionary effect by 79%, and increases the running speed of the algorithm by 4.1%. The proposed improved GA improves GA from the two key operation steps of selection and crossover, and is applied to PID parameter tuning to make the rise time less, the stability time shorter, and the overshoot smaller.
Proportion Integral Differential (PID) parameter tuning; Genetic Algorithm (GA); gene infection crossover; fitness function; transfer function modeling
TM383.4
A
1001-9081(2022)05-1634-08
10.11772/j.issn.1001-9081.2021050745
2021⁃05⁃10;
2021⁃09⁃12;
2021⁃12⁃21。
国家自然科学基金资助项目(61834004)。
刘延飞(1975—),男,陕西咸阳人,教授,博士,主要研究方向:最优控制、嵌入式系统; 彭征(1998—),男,湖南平江人,硕士研究生,主要研究方向:最优控制、嵌入式系统; 王艺辉(1996—),男,福建泉州人,硕士,主要研究方向:多智能体协同、嵌入式系统、目标合围; 王忠(1986—),男,重庆人,副教授,硕士,主要研究方向:多智能体协同、目标合围。
This work is partially supported by National Natural Science Foundation of China (61834004).
LIU Yanfei, born in 1975, Ph. D., professor. His research interests include optimum control, embedded system.
PENG Zheng, born in 1998, M. S. candidate. His research interests include optimum control,embedded system.
WANG Yihui, born in 1996, M. S. His research interests include multi-agent collaboration, embedded system, target enclosing.
WANG Zhong, born in 1986, M. S., associate professor. His research interests include multi-agent collaboration, target enclosing.

