融合学习心理学的人类学习优化算法

孟晗，马良，刘勇

（上海理工大学 管理学院，上海 200093）（∗通信作者电子邮箱menghan_usst@163.com）

融合学习心理学的人类学习优化算法

孟晗*，马良，刘勇

（上海理工大学 管理学院，上海 200093）（∗通信作者电子邮箱menghan_usst@163.com）

针对简单人类学习优化（SHLO）算法寻优精度低和收敛慢的问题，提出了一种融合学习心理学的人类学习优化算法（LPHLO）。首先，结合学习心理学中的小组学习（TBL）理论引入TBL算子，从而在个体经验、社会经验的基础上，增加了小组经验来对个体学习状态进行控制，避免算法早熟收敛；然后，结合记忆编码理论提出了动态调参策略，从而实现个体信息、社会信息、团队信息的有效融合，更好地平衡了算法局部探索和全局开发的能力。选取典型的组合优化难题——背包问题中的两种算例，即单约束背包问题、多约束背包问题进行仿真实验，实验结果表明，所提LPHLO与基本的SHLO算法、遗传算法（GA）和二进制粒子群优化（BPSO）算法等算法相比，在寻优精度和收敛速度方面更具优势，具有更好的解决实际问题的能力。

简单人类学习优化算法；学习心理学；学习策略；小组学习算子；动态调参策略

0 引言

简单人类学习优化（Simple Human Learning Optimization， SHLO）算法是Wang等［1］提出的一种新的群智能优化算法，该算法模拟了人类学习过程，人类群体通过随机学习、个体学习、社会学习这三种学习方式提升自己的知识和能力。SHLO算法仅使用一个公式就可以完成迭代寻优过程，具有操作简单、易于实现、全局寻优能力强等优点，其竞争力主要来源于对学习算子和算法参数的巧妙设计。与其他典型智能优化算法相比，SHLO算法也展现了其优良特性，例如：与遗传算法（Genetic Algorithm， GA）［2］相比，SHLO的经验库使其具有精英保留机制，群体可以向最优个体学习，从而加快了算法的收敛；与微粒群算法相比，SHLO的随机学习算子使其具有突变功能，扩大了算法的搜索空间。SHLO的这些优点，使其在文本摘要［3］、图像匹配［4］、模糊PID（Proportion-Integration-Differentiation）控制［5］等工程优化问题上得到了广泛的应用。

作为一种新型的群智能算法，SHLO算法性能存在很大的提升空间，学者们近几年提出了一系列改进的SHLO算法。文献［6］中提出了新的人类学习优化算法，在算法中增加重新学习算子，当个体适应度在一定迭代次数内没有得到改善时，重新学习算子就会清除个体的当前最优解。这种做法可以扩大算法的搜索空间，降低算法陷入局部最优的风险，但是清除当前解的操作可能会使算法错过全局最优解，增加算法的运行时间。文献［7］中提出了自适应简化人类学习优化（Adaptive Simplified Human Learning Optimization， ASHLO）算法，引入自适应调参策略在寻优过程中不断调整三种学习方式所占比例，避免算法陷入局部最优，算法收敛精度得到了提高，但是每次迭代重新确定学习概率的方法减慢了算法的收敛。文献［8］中考虑到人类智力服从高斯分布，在算法中引入高斯分布更新策略调整每个个体的学习能力，这一操作保证了群体的多样性，提高了整个群体的寻优效率，强化了算法的全局搜索能力。文献［9］中利用粒子群优化算法具有较好的局部搜索能力，将粒子群优化算法的粒子更新策略应用于SHLO的学习过程，提高了SHLO算法的收敛能力，但增加了陷入局部最优的风险。这些改进在一定程度上提高了原始算法的性能，但对算法自身的迭代公式研究较少，算法仍然存在早熟收敛、后期收敛较慢、容易陷入局部最优解等问题。

SHLO作为一个以人为主体，模拟人类学习的新型智能算法，现有改进主要模拟人类学习特征和与其他算法结合。这些改进都是基于简化的人类学习模型，很少考虑到人的心理给学习带来的影响：例如，在许多情况下，小组学习（Team-Based Learning， TBL）对一个人的学习有很大的帮助。针对上述问题，本文在算法设计中采取类似的思路，聚焦于学习心理学，模拟学习过程中人的心理因素对学习结果产生的影响，首次将学习心理学理论应用于算法改进之中，为算法提供了全新且可行的改进方向。从学习心理学的角度分析SHLO，结合小组学习理论和记忆编码理论在算法中加入小组学习策略和动态学习策略，并设计对应的小组学习算子和动态调参策略。小组学习算子负责增强算法全局搜索能力，提高了算法的寻优精度；动态调参策略负责更好地平衡全局搜索与局部搜索，提高算法的寻优效率，加快算法的收敛。最后将本文算法用于求解经典的非确定性多项式（Nondeterministic Polynomial， NP）问题——背包问题，通过大量仿真实验验证了所提算法的性能。

1 简单人类学习优化算法

SHLO算法［1］的基本概念源于对人类学习行为的模仿研究。从宏观角度看，人类学习方式分为随机学习、个体学习和社会学习。比如，一个人为了提高自己的知识水平，会进行反复的练习：他会由于缺乏先验知识或希望探索新的学习策略而进行随机学习，他可以积累自己的学习经验以指导接下来的学习（个体学习），也可以通过向前辈请教或查阅书籍等方式进行社会学习。标准SHLO算法受到这种简化的人类学习机制的启发，模拟人类学习过程，开发了与之对应的随机学习算子、个体学习算子和社会学习算子，并利用三个学习算子产生新解，经过反复迭代寻找最优值，下面介绍其基本步骤。

1.1 初始化种群

SHLO采用二进制编码框架，每个个体代表一组解，用二进制字符串表示。

1.2 学习算子

1.2.1 随机学习算子

随机学习是开拓新知识的有效途径，为了模仿人类随机学习过程，SHLO开发了随机学习算子，按式（2）进行随机学习：

1.2.2 个体学习算子

个体学习是人们依靠自身经验进行自我提升的学习过程。SHLO开发了个体学习算子，创建了用来储存个体最好经验的个体知识库，如式（3）所示。基于的知识，SHLO可以按式（4）进行个体学习：

1.2.3 社会学习算子

随机学习和个体学习的效率可能比较低，而社会学习可以弥补这个缺陷。SHLO为了进行社会学习，开发了社会学习算子，创建了用于储存社会经验的社会知识库，因此可以基于的知识，按式（5）进行社会学习：

SHLO以特定的概率执行三个学习算子，不断迭代产生新解并寻求全局最优解，如式（6）所示：

2 融合学习心理学的人类学习优化算法

SHLO算法是基于一个简化的人类学习模型，而真正的人类学习是一个极其复杂的过程，存在较大的改进空间。从算法角度分析，基本的人类学习优化算法有两点不足：学习算子的设计具有局限性，如式（4）～（5）所示，仅仅学习群体当前的最好经验以及个体过去的最好经验，限制了个体的学习搜索范围，可能使个体落入局部最优解而无法逃脱；参数设置不够合理，SHLO的参数和对个体学习状态进行控制，决定了个体学习的效果，进而影响算法的寻优性能，如式（6）所示，采取固定的参数难以保证算法在寻优过程中平衡好算法的探索和开发能力，不能保证算法收敛。

作为一个以人类学习为模拟对象的智能算法，从人类学习过程出发，能从源头上弥补SHLO算法的一些不足。在过去的几十年里，学习心理学理论取得了许多成果，能为人类学习提供科学的基础知识。从学习心理学角度分析，基本的人类学习优化算法在学习过程中没有采用高效的学习策略，不能充分发挥个人的学习潜能。为了进一步提高算法的性能，融合学习心理学的人类学习优化算法（Human Learning Optimization algorithm based on Learning Psychology， LPHLO）结合学习心理学理论对人类学习优化算法进行了两个方面的改进：结合小组学习理论，在个体信息和社会信息基础上，增加了小组信息对个体学习状态进行控制，提高了个体搜索效率，解决了个体趋同问题；在增加小组信息之后，三种信息作用权重的选择又是一个新的问题，对此，SHLO引入记忆编码理论提出动态调参策略改善算法参数，及时调整不同学习方式的选择概率，有效利用了各种学习信息，克服了固定参数的弊端，保证了算法的寻优速度。

2.1 引入小组学习理论改进学习算子

在基本SHLO算法中，如式（6）所示，三个学习算子被用来产生新的候选解以搜索最优值。随机学习算子使个体保持学习活力，使其有扩展搜索空间的趋势，有能力探索新的区域。个体学习算子和社会学习算子表示个体的学习动作来源于自己经验的部分和群体经验的部分，每个个体都是通过这两部分的信息来确定运动趋势。因此，在全局最优信息引导下，随着寻优过程的深入，个体学习状态趋同，使得群体多样性丧失，陷入早熟收敛。观察式（2）、（4）～（5）可以发现，SHLO设计了过于简单的学习方式，这是导致算法早熟的主要原因之一。在真实学习环境中，随机学习、个体学习和社会学习不能全面反映一个人的学习过程，人们在很多时候也会进行小组学习。小组学习（TBL）是一种很常见的学习方式，TBL的核心是不同的学习者在完成任务的过程中进行交流，在这种学习模式中，学习者之间有真正的信息沟通。小组学习理论对于人们学习是有益的，Burgess等［10］验证了TBL能调动学生学习的积极性，提高了学生解决问题的能力，改善了学习的效果；Eguchi等［11］验证了TBL能有效提高学生的学习成绩。

鉴于此，LPHLO结合小组学习理论，在算法中引入小组学习算子，用来把小组学习策略加到群体迭代学习过程中。它设定人为一个小组，小组成员根据小组的经验进行学习。小组知识库被用来储存小组最佳经验，如式（7）所示：

LPHLO通过执行随机学习算子、个人学习算子、小组学习算子和社会学习算子产生新的解决方案，如式（9）所示：

2.2 引入记忆编码理论改进参数

小组学习算子的引入，使算法在个体信息和社会信息的基础上增加了小组信息，个体和群体的信息得到了更充分的交流和应用，较好地解决了全局最优信息引导下粒子状态趋同问题，提高了算法的全局寻优能力和寻优精度。但是，不同学习信息的有效融合是影响算法搜索效果的重要因素之一，也是改进学习算子之后要考虑的问题。如式（9）所示，参数、、决定了各学习算子的贡献率，直接影响算法探索能力和开发能力之间的平衡。基本SHLO设置了固定参数，其优化效果有待提高。通常在智能优化算法里，参数动态调整的效果会更好。Wang等［7］对参数和采取了自适应调整策略，有效减轻了参数设置的负担。由此可见，采取动态参数更加合理，正如人们在学习过程中会不断调整自己的学习状态。人们在学习过程中，倾向于总结学习规律，根据不同的学习能力选择更高效的学习策略。记忆编码理论揭示了一系列人类记忆规律，可以帮助人们更好地掌握学习规律，提高学习质量。Craik等［12］验证了年龄差异对学习记忆有影响，揭示了人类记忆变化规律，即随着年龄的增长，盲目随机学习的可能性逐渐降低，根据自身经验以及外界经验学习的能力相对提高。

据此，LPHLO结合记忆编码理论提出了动态学习策略，在学习早期更多地进行随机学习，随着年龄增加更多地进行个体学习以及小组学习。为了模拟动态学习策略，LPHLO在算法中引入了动态调参策略，用迭代次数的增加来模拟人类年龄的变化，、、、分别代表随机学习、个体学习、小组学习、社会学习的贡献率，它们的大小随着迭代次数的变化而变化，其中的值随着迭代次数的增加呈现递减趋势，、的值随着迭代次数的增加呈现递增趋势，如式（10）～（12）所示：

2.3 更新策略

2.4 LPHLO流程

LPHLO的具体步骤如下：

步骤2 学习阶段。在迭代学习过程中，加入小组学习算子和动态调参策略，按照式（10）～（12）得到、、的值，然后按照式（9）生成新一代群体。

步骤3 更新阶段。计算新一代群体的适应度值，根据更新策略分别更新、、。

步骤4 判断终止准则，如果当前迭代次数大于最大迭代次数，则输出所求问题的最优解并终止运行LPHLO；否则转步骤2。

3 实验和结果分析

为了测试本文算法的有效性，选取经典的NP问题——单约束背包问题（0-1 Knapsack Problem， 0-1KP）［13］和多约束背包问题（Multi-constrained KP， MKP）进行仿真实验。实验1按照文献［14］中提出的0-1KP实例产生流程，产生20个0-1KP实例测试算法性能。实验2来自OR-Library的MKP实例，在30个MKP算例上考察本文算法优化多约束背包问题的有效性和可行性。将所提的LPHLO和ASHLO、SHLO、GA、二进制粒子群优化（Binary Particle Swarm Optimization， BPSO）算法［15］以及二进制蝙蝠算法（Binary Bat Algorithm， BBA）［16］这五种算法在每个实例上进行30次对比实验。实验环境如下：计算机CPU为i5-6200U，内存RAM为4 GB，操作系统为Windows 10，编程软件为Matlab 2019a。

3.1 单约束背包问题仿真实验

为了充分测试LPHLO的性能和特点，使用两组共20个大规模0-1KP实例来测试算法的寻优性能。每组10个问题维数分别设置为100、200、400、600、800、1 000、1 200、1 500、2 000、3 000。对于KP的每个实例，重量和价值根据文献［14］产生，即重量在5～20随机取值，价值在50～100随机取值。每组10个实例的容量值分别设置为1 000、2 400、4 000、6 000、8 000、10 000、14 000、16 000、20 000、25 000。维数小于1 000时，种群大小和最大迭代次数分别设置为100、10 000，否则分别设置为200、40 000。每个实例产生后保持不变，算法其他参数设置如下：BBA中，；BPSO中，；GA中，；SHLO中，；ASHLO中，；LPHLO中，。

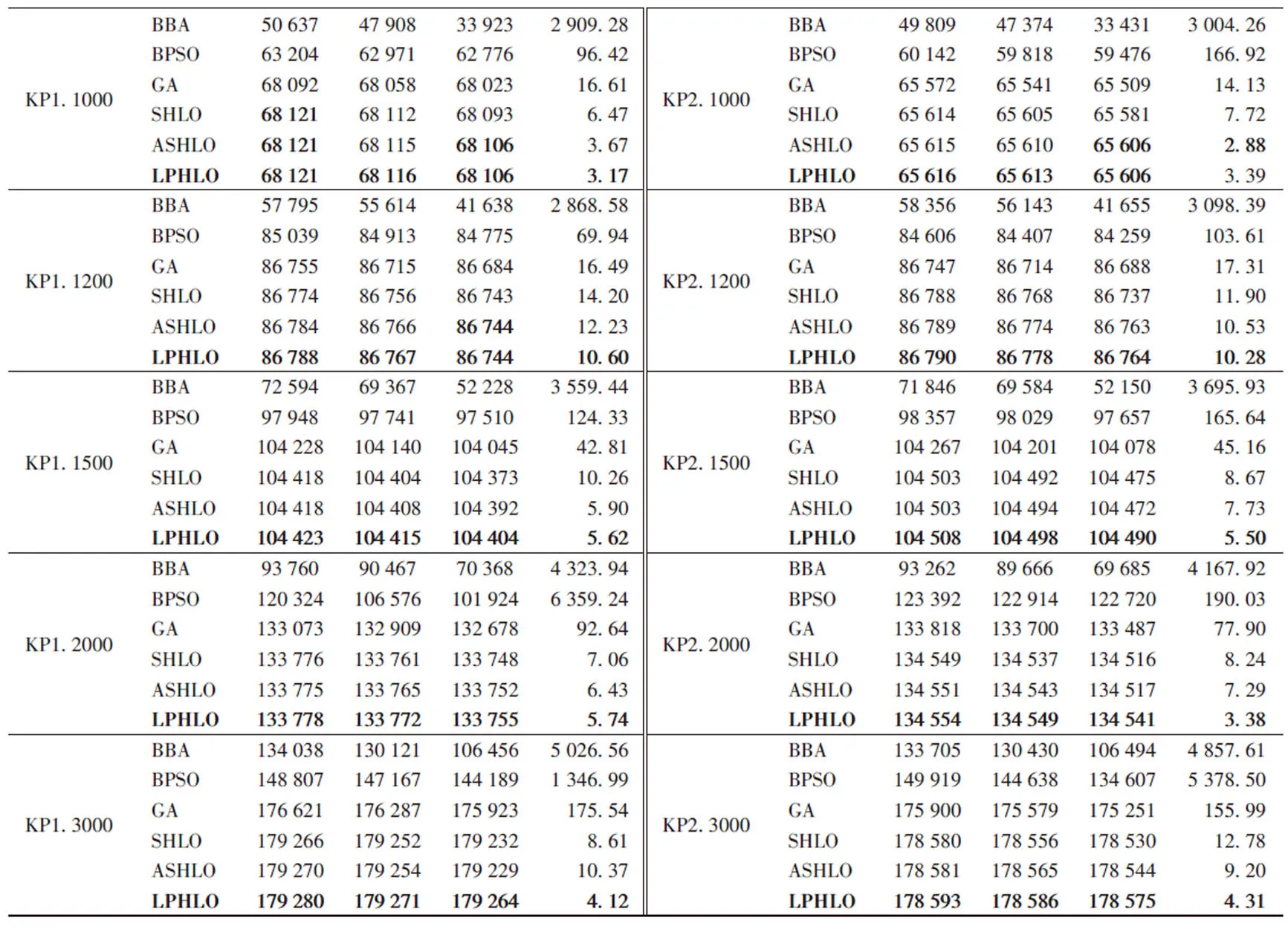
不同算法的0-1KP实例求解结果如表1所示，每个实例上最好的值做加粗处理。其中，第1列是问题类型，如KP1.100表示第1组实验中问题维数为100的0-1KP实例。分别从最优值、平均值、最差值和标准差这4个方面对算法进行全面评估。最优值、平均值可以反映算法的求解精度和寻优能力，最差值、标准差可以反映算法的稳定性和跳出局部极值的能力。可以看出，BBA、BPSO、GA这三种算法获得的优化结果不如LPHLO、ASHLO、SHLO。这是因为人类学习优化算法是天然的二进制编码算法，对二进制问题有更强的求解能力。当问题规模不超过1 000时，LPHLO、ASHLO、SHLO这3种算法无论是求解质量还是求解的稳定性差别并不大；但随着问题维数的增加，解空间呈几何倍增长，特别当问题规模超过1 200时，搜索空间超过21200级，算法在有限迭代次数内仅能开采较小的解空间，造成求解质量的下降，这就对算法摆脱局部最优和勘探新解的能力有了更高的要求。对比发现，LPHLO的最优值、平均值和最差值在所有实例中都是最好的，且随着问题规模的增加，与另外5种算法的差距越来越明显，表明LPHLO有更强的对抗局部极值的能力和更高的寻优精度。同时随着问题规模的增大，各算法求解的稳定性也会下降，LPHLO的标准差除了在KP1.200、KP1.400、KP2.1000这三个实例上略逊于SHLO或ASLHO外，在其余17个实例上始终表现最好，验证了算法的鲁棒性和求解的稳定性。

表1 单约束背包问题的结果对比Tab. 1 Comparison of results on 0-1KPs

3.2 多约束背包问题仿真实验

为了评估LPHLO在MKP实例上的性能，使用OR-Library的MKP基准进行测试。前15个算例使用测试基准mknapcbl（5.100），它有5个约束和100个物品，后15个算例使用测试基准mknapcb4（10.100），它有10个约束和100个物品。为了保证算法对比的公平性，实验采用每种算法对目标函数计算50 000次。对30个算例的测试结果如表2所示，其中第1列表示问题类型，如5.100.00代表mknapcbl（5.100）中的第1个算例，第2列表示OR-Library中的最优解。

由表2的实验结果可知，LPHLO在所有实例上都能得到比ASHLO、SHLO、GA、BPSO、BBA这五种算法更好的结果，并且在每个实例上都能找到目前已知最优解，表现出较优的解决多约束背包问题的能力。

表1和表2验证了LPHLO具有较优的收敛精度，为了进一步验证LPHLO的收敛速度，图1给出了部分背包问题的迭代收敛曲线。所有这些曲线都显示了在一个独立测试中发现最佳值的变化过程，并且每个图中使用的测试是在30个独立测试中达到最佳值的测试。为了更清晰地对比6种算法，图1中的适应度函数值经过了指数形式处理得到。

观察图1可以发现，LPHLO在6个不同的背包实例上都能以最少的迭代次数收敛到目前最好的解。因为小组学习算子增加了种群信息交流的深度，动态调参策略提高了种群的信息交流速度，所以个体能更高效地进行学习，使LPHLO在寻优过程中能够更快地收敛。

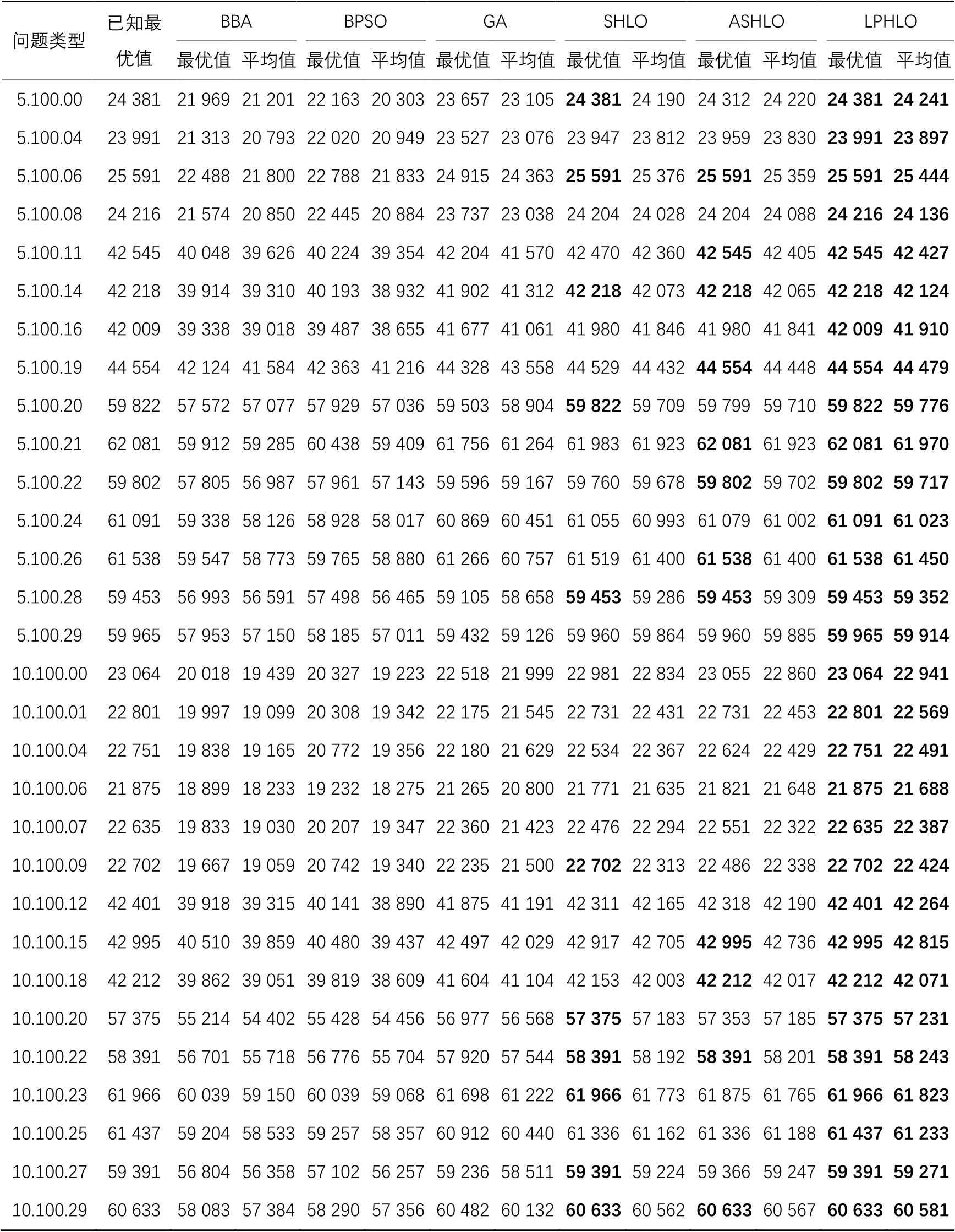
表2 多约束背包问题的结果对比Tab. 2 Comparison of results on MKPs

为了进一步检验两组实验中不同方法准确性差异的显著性，对6种算法在50个背包实例上的测试结果进行Freidman统计检验，结果如图2所示，其中每个算法原点为其平均序值，线段为临界阈值的大小，若两种算法有交集，则说明没有显著差异，否则有显著差异。统计检验表明，LPHLO在Friedman检验中排名第一，和50个已知最优值一样。BBA、BPSO、GA、SHLO、ASHLO这五种算法得到的解和已知最优值之间存在显著差异，而LPHLO的结果和目前已知最优结果之间的差异不具有统计学意义，直观地表明了LPHLO优于BBA、BPSO、GA、SHLO、ASHLO这五种算法，且给出了目前已知最优的结果。

表1～2以及图1～2的结果表明，本文提出的LPHLO具有较高的寻优精度、较快的收敛速度以及解决实际问题的可靠性等优势，这得益于人类学习优化算法和学习心理学理论的结合。从学习心理学角度分析人类学习优化算法，结合小组学习理论引入小组学习算子，使个体和群体之间的信息得到了充分的交流，提升了学习的效果，提高了算法的求解精度；结合记忆编码理论引入动态调参策略，增加了学习的灵活性，使算法更易跳出局部最优，提高了算法的寻优效率。小组学习算子和动态调参策略的配合使用，使算法的寻优精度和收敛速度得到同步提升，提高了算法的鲁棒性以及解决实际问题的能力。

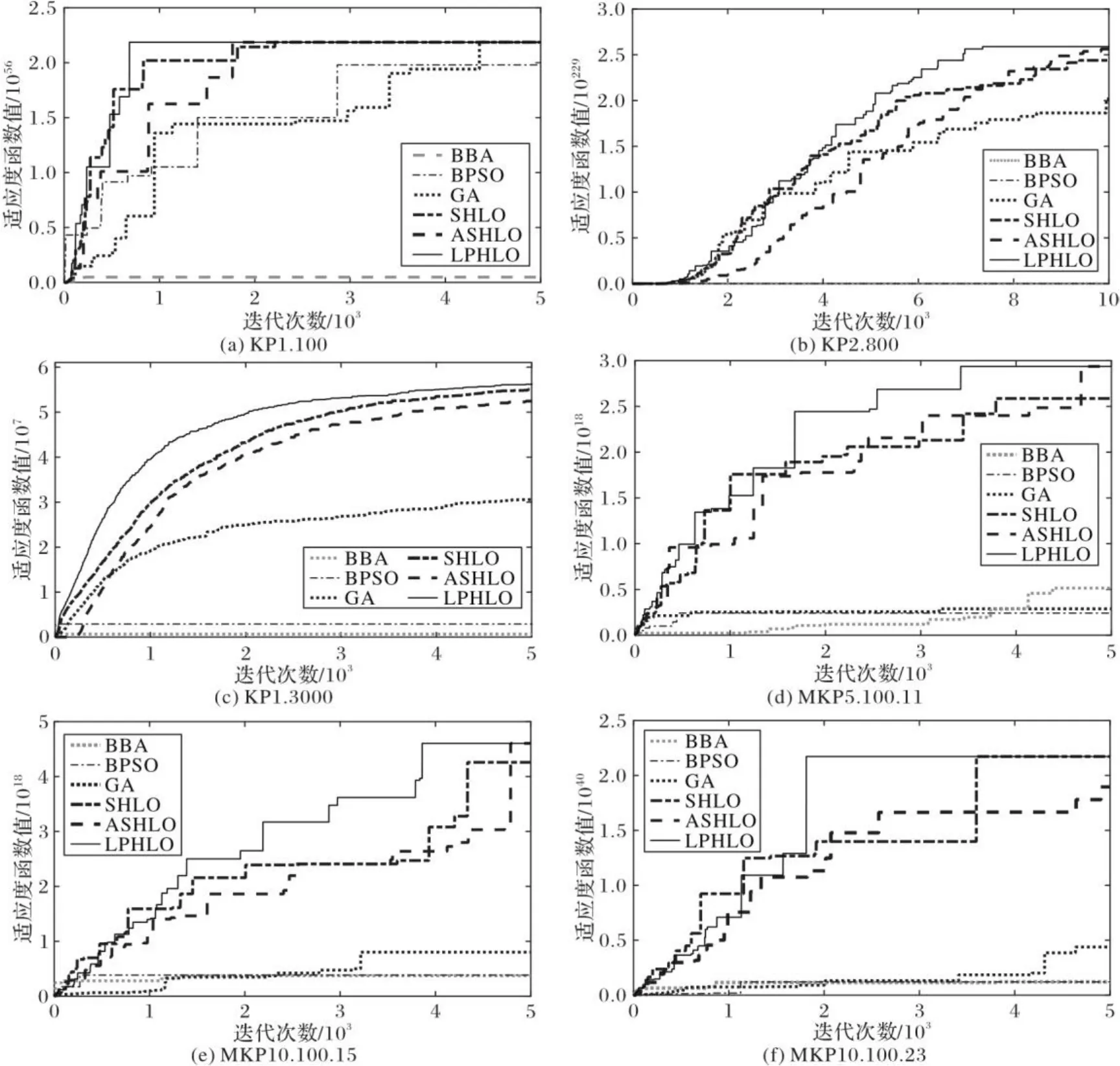
图1 部分背包问题的最优值收敛曲线Fig. 1 Optimal value convergence curves of partial knapsack problems

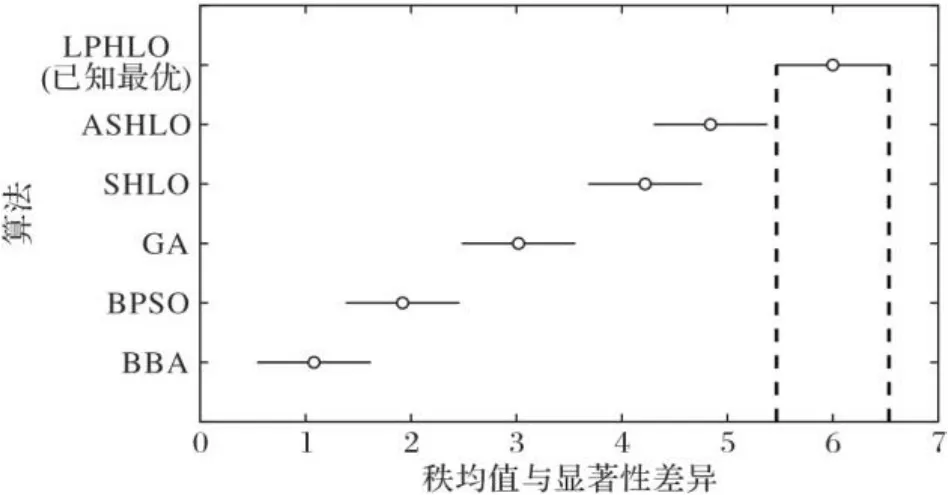
图2 六种算法的Friedman检验结果Fig. 2 Friedman test results of six algorithms

4 结语

针对人类学习优化算法寻优精度不高、收敛较慢的问题，本文提出了融合学习心理学的人类学习优化算法，结合学习心理学理论对人类学习优化算法进行改进。从学习心理学角度分析，所提算法通过提升人类学习效果来提高算法性能。结合小组学习理论提出了小组学习策略，然后结合记忆编码理论提出了动态学习策略，并在算法中引入了与两种学习策略相对应的小组学习算子和动态调参策略，提高了算法的收敛速度和寻优精度，增强了算法解决实际问题的能力。将提出的LPHLO应用于求解经典的NP问题——背包问题，实验结果验证了LPHLO的可行性和有效性。下一步的工作是将LPHLO应用到其他类型的组合优化问题中，如应急选址问题等。

[1] WANG L， NI H Q， YANG R X， et al. A simple human learning optimization algorithm ［C］// Proceedings of the 2014 International Conference on Intelligent Computing for Sustainable Energy and Environment and the 2014 International Conference of Life System Modeling and Simulation， CCIS 462. Berlin： Springer， 2014：56-65.

[2] LIEPINS G E， HILLIARD M R. Genetic algorithms： foundations and applications ［J］. Annals of Operations Research， 1989， 21（1）： 31-57.

[3] ALIGULIYEV R， ALIGULIYEV R， ISAZADE N. A sentence selection model and HLO algorithm for extractive text summarization ［C］// Proceedings of the 2016 IEEE 10th International Conference on Application of Information and Communication Technologies. Piscataway： IEEE， 2016： 1-4.

[4] 张旭，郭东恩.基于DCT与自适应人类学习优化算法的图像匹配算法［J］.电子测量与仪器学报，2018，32（6）：148-154.（ZHANG X， GUO D E. Image matching approach based on DCT and adaptive human learning optimization algorithm ［J］. Journal of Electronic Measurement and Instrumentation， 2018， 32（6）： 148-154.）

[5] 张安发，张玮，童鑫，等.基于人类学习优化算法的变论域模糊PID控制研究［J］.工业控制计算机，2017，30（7）：45-47.（ZHANG A F，ZHANG W， TONG X， et al. Variable universe fuzzy-PID control based on human learning optimization algorithm ［J］. Industrial Control Computer， 2017， 30（7）： 45-47.）

[6] WANG L， YANG R X， NI H Q， et al. A human learning optimization algorithm and its application to multi-dimensional knapsack problems ［J］. Applied Soft Computing， 2015， 34： 736-743.

[7] WANG L， NI H Q， YANG R X， et al. An adaptive simplified human learning optimization algorithm ［J］. Information Sciences， 2015， 320： 126-139.

[8] WANG L， AN L， PI J X， et al. A diverse human learning optimization algorithm ［J］. Journal of Global Optimization， 2017， 67（1/2）： 283-323.

[9] WANG L， PEI J， MENHAS M I， et al. A Hybrid-coded Human Learning Optimization for mixed-variable optimization problems ［J］. Knowledge-Based Systems， 2017， 127： 114-125.

[10] BURGESS A， VAN DIGGELE C， ROBERTS C， et al. Team-based learning： design， facilitation and participation ［J］. BMC Medical Education， 2020， 20（S2）： Article No.461.

[11] EGUCHI H， SAKIYAMA H， NARUSE H， et al. Introduction of team-based learning improves understanding of glucose metabolism in biochemistry among undergraduate students ［J］. Biochemistry and Molecular Biology Education， 2021， 49（3）： 383-391.

[12] CRAIK F I M， SALTHOUSE T A. The Handbook of Aging and Cognition ［M］. 3rd ed. New York： Psychology Press， 2008： 445-484.

[13] 陈桢，钟一文，林娟.求解0-1背包问题的混合贪婪遗传算法［J］.计算机应用，2021，41（1）：87-94.（CHEN Z， ZHONG Y W， LIN J. Hybrid greedy genetic algorithm for solving 0-1 knapsack problem ［J］. Journal of Computer Applications， 2021， 41（1）： 87-94.）

[14] ZOU D X， GAO L Q， LI S， et al. Solving 0-1 knapsack problem by a novel global harmony search algorithm ［J］. Applied Soft Computing， 2011， 11（2）： 1556-1564.

[15] EL-MALEH A H， SHEIKH A T， SAIT S M. Binary Particle Swarm Optimization （BPSO） based state assignment for area minimization of sequential circuits ［J］. Applied Soft Computing， 2013， 13（12）： 4832-4840.

[16] MIRJALILI S， MIRJALILI S M， YANG X S. Binary bat algorithm ［J］. Neural Computing and Applications， 2014， 25（3/4）： 663-681.

Human learning optimization algorithm based on learning psychology

MENG Han*， MA Liang， LIU Yong

（Business School，University of Shanghai for Science and Technology，Shanghai200093，China）

Aiming at the problems of low optimization accuracy and slow convergence of Simple Human Learning Optimization （SHLO）algorithm， a new Human Learning Optimization algorithm based on Learning Psychology （LPHLO） was proposed. Firstly， based on Team-Based Learning （TBL） theory in learning psychology， the TBL operator was introduced， so that on the basis of individual experience and social experience， team experience was added to control individual learning state to avoid the premature convergence of algorithm. Then， the memory coding theory was combined to propose the dynamic parameter adjustment strategy， thereby effectively integrating the individual information， social information and team information. And the abilities of the algorithm to explore locally and develop globally were better balanced. Two examples of knapsack problem of typical combinatorial optimization problems， 0-1 knapsack problem and multi-constraint knapsack problem， were selected for simulation experiments. Experimental results show that， compared with the algorithms such as SHLO algorithm， Genetic Algorithm （GA） and Binary Particle Swarm Optimization （BPSO） algorithm， the proposed LPHLO has more advantages in optimization accuracy and convergence speed， and has a better ability to solve the practical problems.

Simple Human Learning Optimization (SHLO) algorithm; learning psychology; learning strategy; Team-Based Learning (TBL) operator; dynamic parameter adjustment strategy

TP273

A

1001-9081（2022）05-1367-08

10.11772/j.issn.1001-9081.2021030505

2021⁃04⁃02；

2021⁃06⁃01；

2021⁃06⁃02。

上海市“科技创新行动计划”软科学研究重点项目（18692110500）；上海市哲学社会科学规划项目（2019BGL014）；上海市高原科学建设项目（第2期）；上海理工大学科技发展项目（2020KJFZ040）。

孟晗（1996—），女，河南漯河人，硕士研究生，主要研究方向：系统工程、智能优化； 马良（1964—），男，上海人，教授，博士，主要研究方向：管理科学与工程、系统工程； 刘勇（1982—），男，江苏金湖人，副教授，博士，主要研究方向：智能优化、服务网络设计与优化、系统工程。

This work is partially supported by Key Soft Science Research Project of Shanghai “Scientific and Technological Innovation Action Plan” （18692110500），Shanghai Philosophy and Social Science Planning Project （2019BGL014）， Shanghai Plateau Science Construction Project （Phase 2），Science and Technology Development Project of University of Shanghai for Science and Technology （2020KJFZ040）.

MENG Han， born in 1996， M. S. candidate. Her research interests include system engineering， intelligent optimization.

MA Liang， born in 1964， Ph. D.， professor. His research interests include management science and engineering， system engineering.

LIU Yong， born in 1982， Ph. D.， associate professor. His research interests include intelligent optimization， service network design and optimization， system engineering.