基于局部策略交互探索的深度确定性策略梯度的工业过程控制方法

邓绍斌，朱军，周晓锋*，李帅，刘舒锐

（1.中国科学院 网络化控制系统重点实验室，沈阳 110016； 2.中国科学院 沈阳自动化研究所，沈阳 110169；3.中国科学院 机器人与智能制造创新研究院，沈阳 110169； 4.中国科学院大学，北京 100049）（∗通信作者电子邮箱zhouxf@sia.cn）

基于局部策略交互探索的深度确定性策略梯度的工业过程控制方法

邓绍斌1，2，3，4，朱军1，2，3，周晓锋1，2，3*，李帅1，2，3，4，刘舒锐1，2，3

（1.中国科学院 网络化控制系统重点实验室，沈阳 110016； 2.中国科学院 沈阳自动化研究所，沈阳 110169；3.中国科学院 机器人与智能制造创新研究院，沈阳 110169； 4.中国科学院大学，北京 100049）（∗通信作者电子邮箱zhouxf@sia.cn）

为了实现对非线性、滞后性和强耦合的工业过程稳定精确的控制，提出了一种基于局部策略交互探索的深度确定性策略梯度（LPIE-DDPG）的控制方法用于深度强化学习的连续控制。首先，使用深度确定性策略梯度（DDPG）算法作为控制策略，从而极大地减小控制过程中的超调和振荡现象；同时，使用原控制器的控制策略作为局部策略进行搜索，并以交互探索规则进行学习，提高了学习效率和学习稳定性；最后，在Gym框架下搭建青霉素发酵过程仿真平台并进行实验。仿真结果表明，相较于DDPG，LPIE-DDPG在收敛效率上提升了27.3%；相较于比例-积分-微分（PID），LPIE-DDPG在温度控制效果上有更少的超调和振荡现象，在产量上青霉素浓度提高了3.8%。可见所提方法能有效提升训练效率，同时提高工业过程控制的稳定性。

工业过程控制；深度强化学习；深度确定性策略梯度；局部策略交互探索；青霉素发酵过程

0 引言

随着现代化工业过程集成化加深，动态控制性能要求越来越高。精准有效的控制可以促进工业过程的稳定、产品质量的提高和经济效益的增长，因此控制策略扮演着越来越重要的角色。

大多数工业过程是非线性、滞后性和强耦合的多输入单输出过程，青霉素发酵过程是典型之一，面对不同的工业要求，往往需要制定不同的控制策略。针对受时变干扰和时不变不确定的蒸馏塔过程，Bansal等［1］使用单变量比例-积分-微分（Proportion-Integration-Differentiation， PID）控制器对蒸馏塔过程进行控制，取得了较好的经济效益，但面对多目标的情况存在控制不足的问题；Asteasuain等［2］提出了使用多变量PID控制器对连续搅拌釜反应器进行控制，实现了单变量到多变量的控制，但未考虑到控制系统的自适应性；赵海丞等［3］提出变调节周期PID方法来控制温度系统，解决了温控系统精度受限的问题，一定程度上提高了系统自适应性；包元兴等［4］提出模糊PID与跟随控制相结合的控制策略，实现了对具有纯滞后、大惯性及通道间强耦合特性炉温的准确控制，进一步提高了系统自适应性。PID参数少、便于掌握，但随着控制过程复杂化，参数调整往往需要专家长时间的调整。

为了提高复杂工业系统的控制性能，研究者们引入了不同的控制方法。吴鹏松等［5］采用多变量解耦和内模控制，实现了对具有大滞后、强耦合特性系统的稳定控制；张惠琳等［6］针对复杂的浮标控制系统，提出了基于双闭环反馈回路的模糊PID定深控制，实现了对浮标良好的控制和稳定；庄绪君等［7］通过遗传算法和迭代动态规划结合的混合优化控制策略，解决了青霉素发酵模型的不确定性敏感的问题。但上述方法都无法实现在线学习，造成控制系统设计过程复杂，同时无法满足最优控制。

深度强化学习是一种利用数据驱动，通过与系统交互实现端到端控制的方法，将深度强化学习应用到这类工业控制过程中，可以有效实现最优控制，再进一步通过对不同场景进行设定，能够有效地提高算法的自适应性。郝鹃等［8］针对车间不确定环境调度问题，提出了使用平均强化学习进行控制，实现了车间的自适应控制，但该方法的应用局限于离散动作的工业环境；王建平等［9］针对工业制造中传统二连杆控制效率低和适用性低等缺点，提出了使用基于深度强化学习的方法，实现了连续控制稳定性和适用性的提高，但忽略了复杂工业数据导致训练困难的问题。

针对非线性、滞后性和强耦合的工业过程难以满足控制器的在线稳定训练需求和精准稳定的连续控制需求，本文提出了基于局部策略交互探索的深度确定性策略梯度（Local Policy Interaction Exploration-based Deep Deterministic Policy Gradient， LPIE-DDPG）的控制方法。一方面，深度确定性策略梯度（Deep Deterministic Policy Gradient， DDPG）有很强的自我学习能力，可以根据不同环境学习最优控制策略，在最优控制中展现出直接自适应性。另一方面，针对DDPG学习效率不足，引入PID在工业控制中的控制逻辑，将PID的控制策略以专家经验的形式作为局部策略，并通过交互规则学习PID的控制策略，最后进行再探索和再利用，完成最优策略的学习。其中，交互规则保证了代理在强相似的工业数据中正常学习，在线局部策略提高了代理的收敛速度，再探索和再利用保留了代理的寻优能力，使得DDPG能收敛于最优策略。最后，本文通过具有代表性的多输出单输出过程——青霉素发酵过程进行仿真实验，验证了本文方法的有效性。

1 基于LPIE‑DDPG的控制方法

1.1 深度强化学习理论

强化学习是机器学习中一种以系统状态为输入、以策略函数为输出的方法，作为自监督的学习方式，一方面基于行动和奖励数据进行反复训练，优化行动策略，另一方面自主地与环境互动，观测并获取环境反馈［10］。

深度强化学习是深度学习与强化学习的结合，深度神经网络克服了强化学习方法只能应用于非凸策略函数的局限，解决了强化学习算法不能应用到非常复杂的决策情景的问题，实现了端到端的学习。

1.2 DDPG

DDPG是深度强化学习中一种基于策略的强化学习方法，可以在连续行为空间中寻找最优策略［11］。

对行动价值网络的训练是基于最小化损失函数：

而现实网络中演说家网络使用策略梯度算法更新的参数为：

网络参数复制采用软更新方式：

1.3 LPIE-DDPG

DDPG仍然存在如何权衡探索和利用的矛盾，学习过程中样本效率低，学习成本高。针对学习效率不足的问题，Hou等［12］使用优先经验重放池代替经验重放缓冲池，可以极大缩短网络总训练时间。但采用比例优先性定义时，经验被抽取的概率正比于经验时序误差值，时序误差值越大，经验被回放的概率更大。因此在工业过程中，非良性控制经验将在回放经验池被一直回放，良性控制的经验得不到回放，代理的学习效果受时序误差离群值的不利影响，优先经验重放池失效。

在模仿学习中，代理像人类专家那样执行一种行为，最大化预期总回报，可以有效地解决探索的问题，但是由于代理通常只模仿专家的标注行为，代理的表现不能超过主题专家或主管［13］。

本文将专家知识应用到探索和策略估计中，提出了基于局部策略交互探索的深度确定性策略梯度算法，通过在线收集原控制器的控制经验，以模仿学习的方式，加快训练智能体，LPIE-DDPG的结构如图1所示。

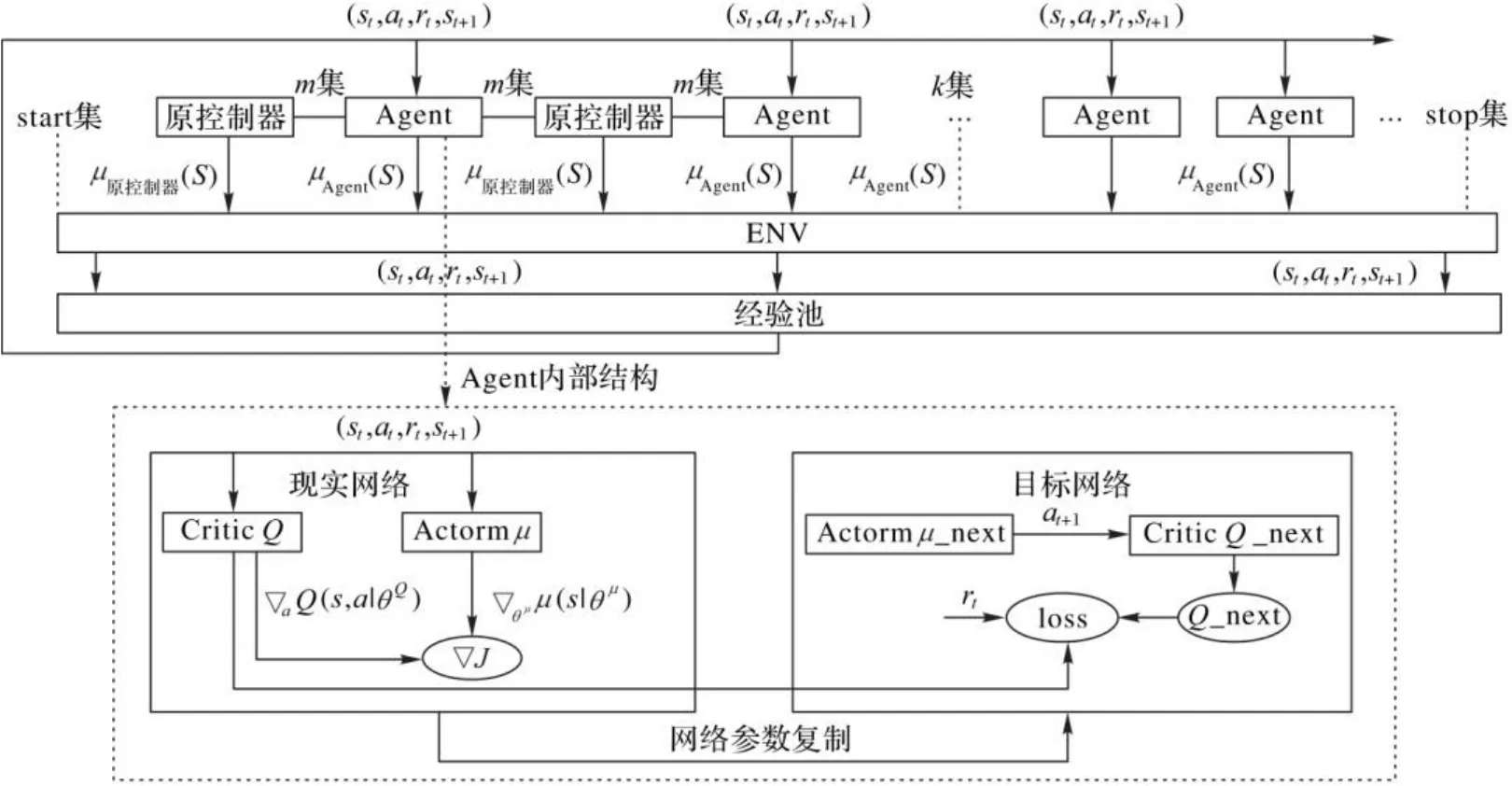
图1 LPIE-DDPG的结构Fig. 1 Structure of LPIE-DDPG

Agent内部结构（DDPG）：现实网络中演说家Actor从经验池中取出作为输入，并输出一个表示从连续动作空间中选择的动作的单一实值，经过环境得到当前奖励，随后目标网络中演说家Actor根据下一个状态输出动作并传给目标网络中评论家Critic。

基于局部策略交互探索（Local Policy Interaction Exploration， LPIE）的流程结构包括以下两部分。

策略更新 随机地从经验池取出经验进行网络更新。

探索阶段 使用Agent网络进行自主探索，通过试错的形式完成搜索和经验获取。

策略更新 从经验池取出经验进行网络更新。

自由探索保证了Agent网络更新不会陷入局部策略，朝着最优策略探索和学习。

LPIE-DDPG算法的具体步骤如算法1所示。

算法1 基于局部策略交互探索的深度确定性策略梯度。

3） 获取初始状态

7） else

9） end if

13） if 达到网络的策略优化更新条件then：

15） 评论家根据式（1）更新网络参数

16） 演说家根据式（2）更新网络参数

18） end if

19） end for

20） end for

2 基于LPIE‑DDPG的青霉素仿真控制

将深度强化学习控制应用到多输入单输出的工业过程的控制流程如下：

1）建立实际系统交互模型。

2）根据实际系统模型建立马尔可夫模型。

3）验证实际系统交互模型的准确性和马尔可夫模型的可行性。

4）根据马尔可夫模型设置模型参数，如状态空间、动作空间、奖励函数等。

5）借鉴原控制器的控制策略，对代理进行多次训练。

6）将代理应用到控制过程，实现对系统的有效控制。

2.1 青霉素发酵过程

青霉素仿真过程是青霉素发酵的一系列过程：青霉素菌种在合适的培养基、PH、温度和通气搅拌等发酵条件下进行生长和合成青霉素的代谢活动［14］。青霉素发酵过程用到发酵罐、冷水调节器、热水调节器、搅拌器和酸碱液调节器，青霉素生产发酵过程的流程如图2所示。

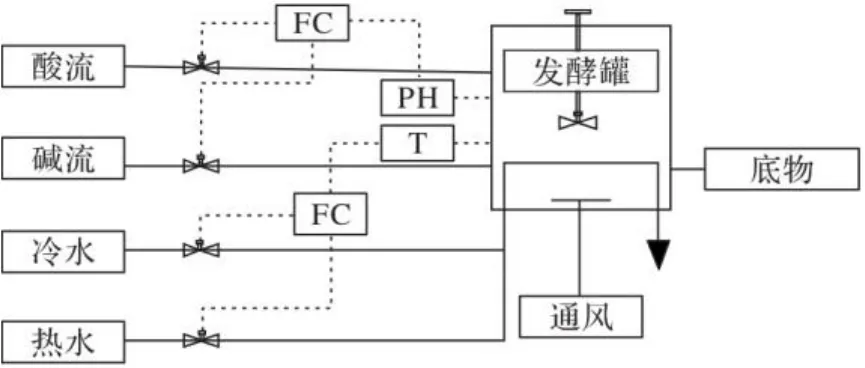
图2 青霉素发酵过程Fig. 2 Penicillin fermentation process

青霉素发酵过程是一个典型的非线性、强耦合和滞后性的间歇过程。青霉素发酵过程被划分为两个阶段：菌体生长期和青霉素合成期［15］。青霉素发酵过程是一个长时间持续的生产过程，其总过程大约在400 h。前一个阶段是菌种生长阶段，持续50 h～60 h，后两个阶段是青霉素合成和菌体衰老阶段，持续340 h～350 h。在不同时期，菌体的生长环境又受诸多因素影响，在前两个阶段，青霉素生长的最佳温度是303 K，最佳PH是6.2～6.5，在后两个阶段，青霉素合成的最佳温度是298 K，最佳PH是6.5～6.9。这使得青霉素发酵过程是一个非线性和多动态的过程，并且发酵过程有9个初始变量、7个过程变量，这使得青霉素发酵过程是一个多输入和强耦合过程。

2.2 青霉素发酵马尔可夫模型

本文选取的研究对象是青霉素发酵过程，青霉素发酵过程的控制与强化学习结合的前提就是建立青霉素发酵的马尔可夫模型。定义青霉素发酵的马尔可夫模型如图3所示：是由青霉素发酵过程的初始状态和可变的操纵变量组成的状态空间，是由青霉素发酵过程的可控变量组成的动作空间，是青霉素发酵过程不同状态之间的转移概率，是在当前状态执行策略获得的即时奖励。

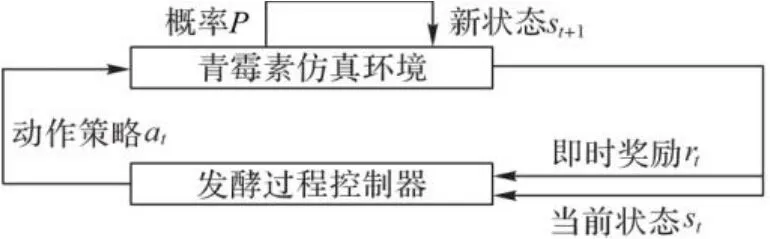
图3 青霉素发酵马尔可夫模型Fig. 3 Markov model of penicillin fermentation

2.3 深度强化学习状态参数

青霉素合成期和菌体自溶期是青霉素合成的关键时期，温度和PH是青霉素合成的关键影响因素，因此本文选取青霉素合成期和菌体自溶期作为实验的背景，青霉素合成过程中以温度控制作为实验内容。针对选取实验内容的实际控制情况，青霉素发酵过程马尔可夫模型的具体参数规定如下：

在保证PH稳定控制的情况下，基于生化反应各个状态值的强耦合性和强相关性，选择当前时刻的氧气浓度、菌体浓度、青霉素浓度（g/L）、培养基体积（L）、二氧化碳浓度、发酵器反应温度和温度差作为状态空间参数。

根据实际控制原则，选择实际控制过程中的被控变量-冷水值作为控制动作。

转移概率取决于当前状态执行动作策略后的新状态。

由于青霉素合成的需要，温度应保持在298 K，因此，奖励函数定义如下：

3 仿真实验及结果分析

3.1 仿真环境

本文的仿真环境是基于Matlab/Simulink环境的青霉素发酵过程仿真平台［16］，使用Python语言，在Gym框架下完成了青霉素仿真模型的迁移。

部分主要状态方程如生物质浓度的计算式为：

温度对微生物比生长速率的影响为：

青霉素浓度的生产用非生长伴随产物形成动力学模型表示：

考虑到温度对发酵过程的影响，本文对完成控制过程的目标设定为：在PH稳定控制的情况下，实现温度值调控的低超调和低振荡。

3.2 实验设置

1）神经网络参数。

LPIE-DDPG网络分为演说家网络（Actor）和评论家网络（Critic），输入神经元数和输出神经元数分别对应状态个数和动作个数，隐含神经元数由实验测试所得，根据损失函数的下降趋势，分别确定学习率的大小，激活函数选择能使模型收敛速度稳定的ReLU（Rectified Linear Unit）函数，具体神经网络参数设置如表1所示。

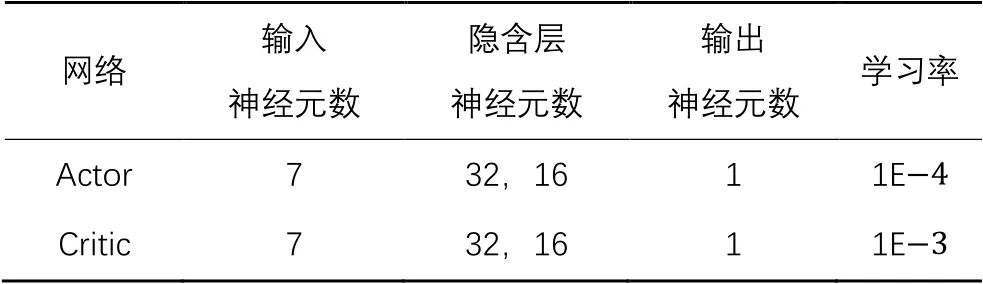
表1 神经网络参数设置Tab. 1 Neural network parameter setting

2）仿真平台初始参数。

在仿真模型中，故障变量包含通风率、搅拌机功率和底物的喂养速率。通风率噪声设置为1 L/h，搅拌功率噪声设置为0.06 W，底物的喂养速率不变。仿真平台其他初始参数如表2所示，其中青霉素浓度指青霉素产量在培养基中的占比，发酵器反应温度是在发酵过程中受外界环境和产生热影响的温度值。

3）算法超参数。

训练总集数为2 000，总步数为200步，折扣因子和经验池容量等超参数的设置如表3所示。

本文规定3个指标来对控制策略进行评价，分别为温度变化、青霉素产量和抗干扰能力。其中，温度变化指控制温度和目标温度298 K的差值大小，青霉素产量为在培养基中的青霉素浓度，抗干扰能力为在干扰信号下对温度的稳定控制能力（相同条件下，温度变化差值越小，青霉素产量越高，抗干扰能力越强，控制策略越优）。

3.3 结果分析

训练过程如图4所示，其中15 000为PID控制情况下每集的奖励累加，并将其作为局部策略引入到DDPG。此外，还将LPIE引入到DQN（Deep Q-learning Network）中，形成局部策略交互探索DQN（Local Policy Interaction Exploration-based Deep Q-learning Network， LPIE-DQN）。轴是训练集数，轴是平均奖励，考虑到奖励受训练过程中探索的影响，本文采用9∶1的奖励累加形式，具体如式（12）所示：

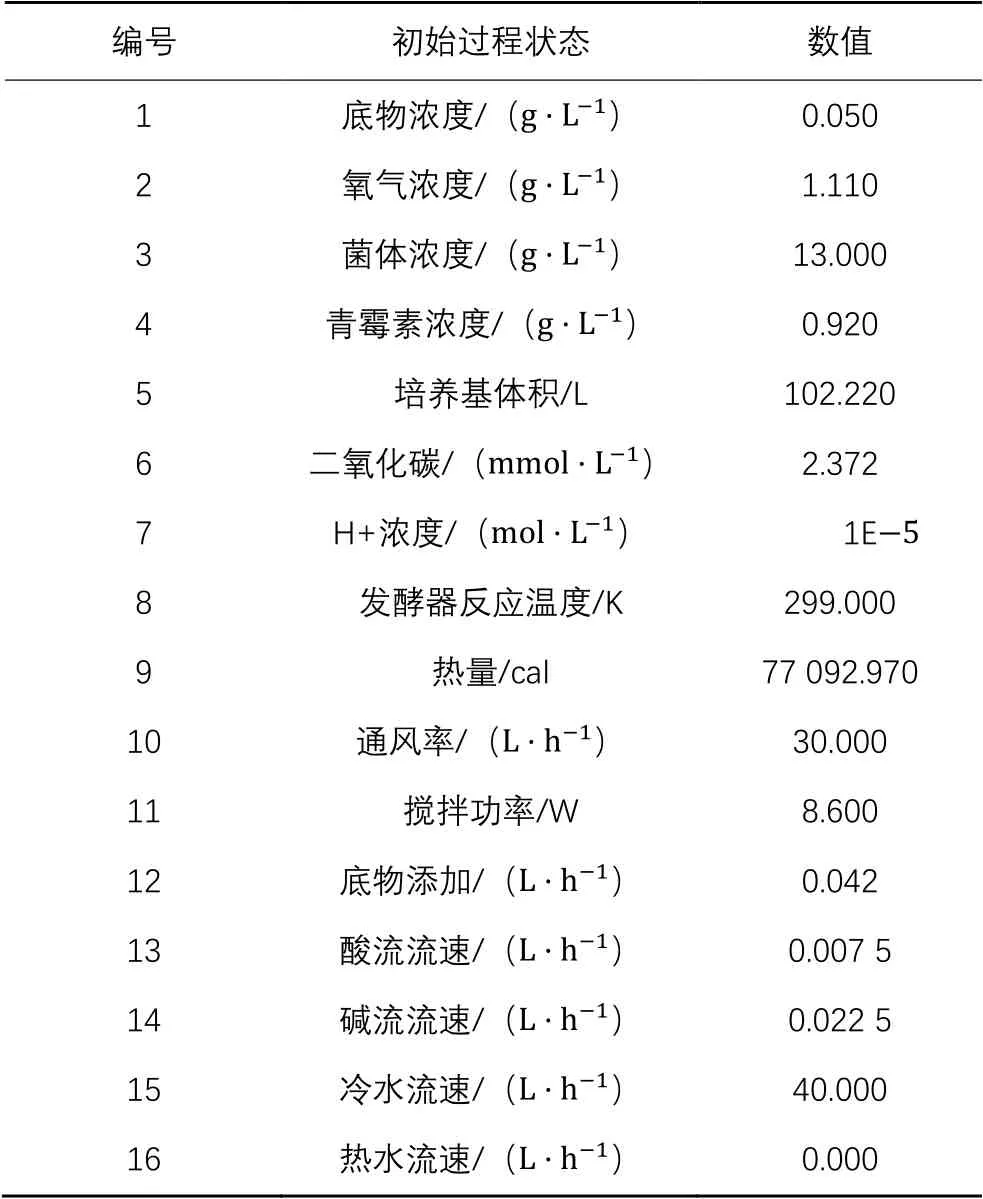
表2 青霉素发酵过程变量的初始值Tab. 2 Initial values of penicillin fermentation process variables

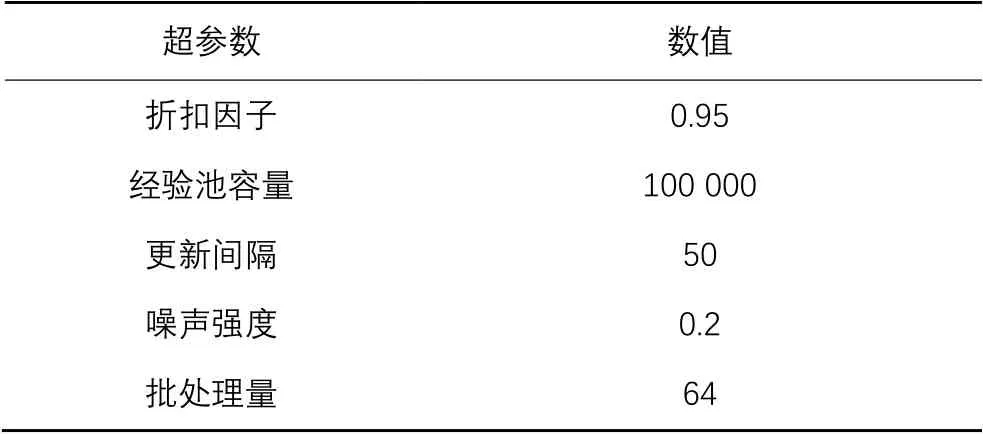
表3 算法超参数设置Tab. 3 Algorithm hyperparameter setting

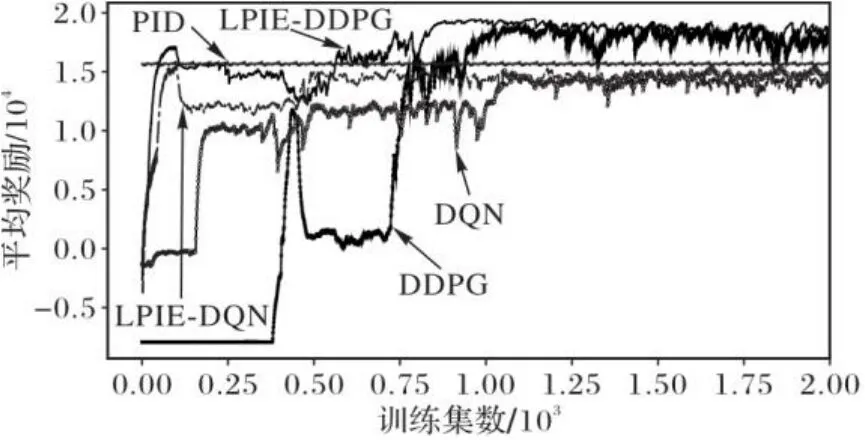
图4 不同算法随迭代次数变化的奖励值Fig. 4 Reward values of different algorithms changing with number of iterations

相较于DDPG，LPIE-DDPG迅速地在100集左右达到局部收敛，并在800集处达到最优，收敛总平均奖励达到18 000，收敛效率提升了27.3%。此外，还对比了DQN和LPIE-DQN的学习效率，LPIE-DQN相较DQN更早达到收敛，在100集就完成了局部收敛，具体结果如表4所示。

通过对代理进行仿真训练，生成最优代理。最优代理对青霉素发酵过程的控制结果如下3个指标所示。

1）温度变化指标。在初始温度为299 K和无干扰的条件下，不同方法的温度变化如图5所示。从图5可以看出，相较于PID和LPIE-DQN，LPIE-DDPG的温度控制表现出无超调和无振荡。

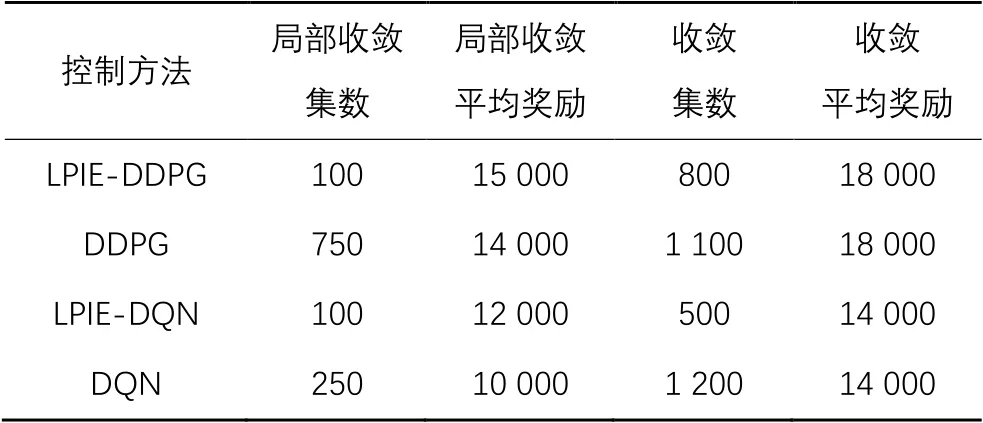
表4 不同方法的学习效率对比Tab. 4 Comparison of learning efficiency of different methods

2）青霉素产量指标。在同等初始条件下，青霉素发酵过程的产量结果如图6所示。由图6可以看出，相较于PID控制，使用LPIE-DDPG控制的青霉素产量浓度值提高了3.8%；相较于LPIE-DQN，LPIE-DDPG具有稳定持续的高青霉素浓度值产量。

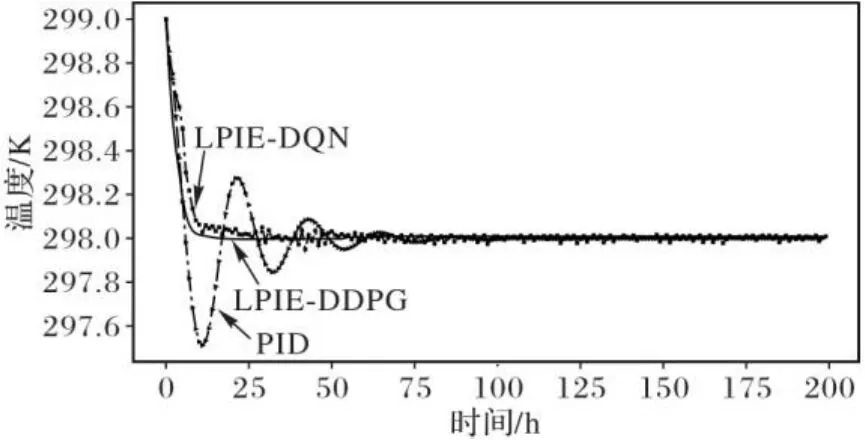
图5 LPIE-DDPG、LPIE-DQN和PID的温度控制效果对比Fig. 5 Comparison of temperature control effect of LPIE-DDPG， LPIE-DQN and PID

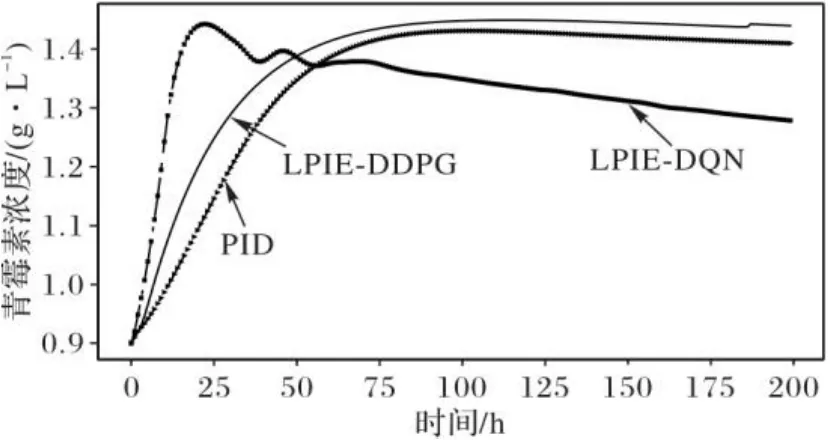
图6 LPIE-DDPG、LPIE-DQN和PID控制下的青霉素产量对比Fig. 6 Comparison of penicillin yield under LPIE-DDPG，LPIE-DQN and PID control

3）抗干扰能力指标。为了检验系统的抗干扰能力，分别在20 h时刻和120 h时刻引入正向脉冲干扰和负向脉冲干扰，结果如图7所示。由图7可以看出，相较于PID和LPIE-DQN，LPIE-DDPG对含有干扰信号的环境具有更加平缓稳定的控制性能。

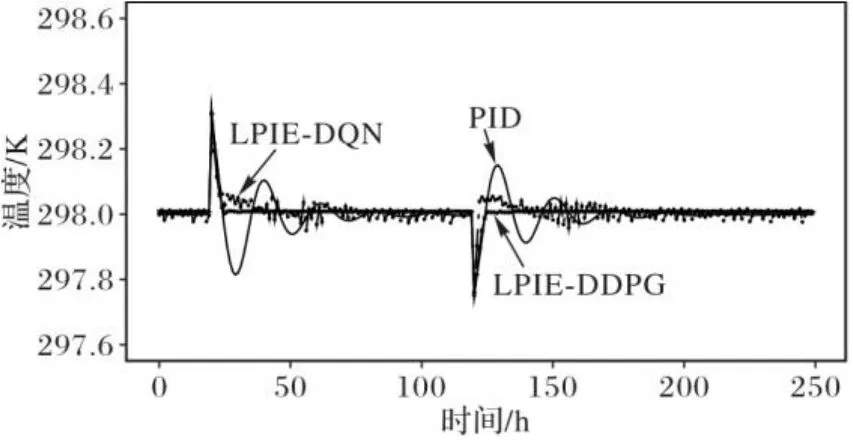
图7 LPIE-DDPG、LPIE-DQN和PID的抗干扰性对比Fig. 7 Comparison of interference resistance of LPIE-DDPG， LPIE-DQN and PID

4 结语

针对工业控制过程的非线性、强耦合、滞后性等特点， 本文提出了基于局部策略交互探索深度确定性策略梯度的控制方法。该方法以DDPG为框架，使用原控制器的控制策略进行学习，以交互探索的方式保证经验回放的可行性，通过自由探索的形式从环境中直接学习，最后通过与工业系统直接交互，完成精准、稳定的控制。基于青霉素仿真模型进行实验，实验结果表明，本文方法有更高的学习效率和更快速的收敛性能，同时提高了工业过程控制的稳定性。

未来的工作将研究在实际生产中应用LPIE-DDPG，通过在探索过程中添加相关安全措施和优化奖励函数来满足实际生产需求、降低生产成本。

[1] BANSAL V， PERKINS J D， PISTIKOPOULOS E N. A case study in simultaneous design and control using rigorous， mixed-integer dynamic optimization models ［J］. Industrial and Engineering Chemistry Research， 2002， 41（4）： 760-778.

[2] ASTEASUAIN M， BANDONI A， SARMORIA C， et al. Simultaneous process and control system design for grade transition in styrene polymerization ［J］. Chemical Engineering Science， 2006， 61（10）： 3362-3378.

[3] 赵海丞，邹应全，刘睿佳，等.温控系统中变调节周期PID算法［J］.计算机应用，2016，36（S2）：116-119.（ZHAO H C，ZOU Y Q， LIU R J， et al. PID algorithm of variable adjustment period based on temperature control system ［J］. Journal of Computer Applications， 2016， 36（S2）： 116-119.）

[4] 包元兴，丁炯，杨遂军，等.强耦合双通道热分析炉温度跟随控制策略研究［J］.测控技术，2016，35（5）：70-74.（BAO Y X， DING J，YANG S J， et al. Study on temperature following control strategy for strong-coupled dual-channel thermal analysis furnace ［J］. Measurement and Control Technology， 2016， 35（5）： 70-74.）

[5] 吴鹏松，吴朝野，周东华.大纯滞后信号解耦内模控制系统研究［J］.化工自动化及仪表，2012，39（9）：1115-1117，1176.（WU P S， WU C Y， ZHOU D H. Research on signal-decoupling internal mode control system with big time lag ［J］. Control and Instruments in Chemical Industry， 2012， 39（9）： 1115-1117， 1176.）

[6] 张惠琳，李醒飞，杨少波，等.深海自持式智能浮标双闭环模糊PID定深控制［J］.信息与控制，2019，48（2）：202-208，216.（ZHANG H L， LI X F， YANG S B， et al. Dual closed-loop fuzzy PID depth control for deep-sea self-holding intelligent buoy ［J］. Information and Control， 2019， 48（2）： 202-208， 216.）

[7] 庄绪君，李宏光.基于遗传算法与迭代动态规划混合策略的青霉素发酵过程优化控制［J］.计算机与应用化学，2013，30（9）：1051-1054.（ZHUANG X J， LI H G. Optimization control strategies combined genetic algorithms and iterative dynamic programming for penicillin fermentation processes ［J］. Computers and Applied Chemistry， 2013， 30（9）： 1051-1054.）

[8] 郝鹃，余建军，周文慧.基于平均强化学习的订单生产方式企业订单接受策略［J］.计算机应用，2013，33（4）：976-979.（HAO J， YU J J， ZHOU W H. Order acceptance policy in make-to-order manufacturing based on average-reward reinforcement learning ［J］. Journal of Computer Applications， 2013， 33（4）： 976-979.）

[9] 王建平，王刚，毛晓彬，等.基于深度强化学习的二连杆机械臂运动控制方法［J］.计算机应用，2021，41（6）：1799-1804.（WANG J P， WANG G，MAO X B， et al. Motion control method of two-link manipulator based on deep reinforcement learning ［J］. Journal of Computer Applications， 2021， 41（6）： 1799-1804.）

[10] 多南讯，吕强，林辉灿，等.迈进高维连续空间：深度强化学习在机器人领域中的应用［J］.机器人，2019，41（2）：276-288.（DUO N X， LYU Q， LIN H C， et al. Step into high-dimensional and continuous action space： a survey on applications of deep reinforcement learning to robotics ［J］. Robot， 2019， 41（2）： 276-288.）

[11] 刘洋，李建军.深度确定性策略梯度算法优化［J］.辽宁工程技术大学学报（自然科学版），2020，39（6）：545-549.（LIU Y， LI J J. Optimization of deep deterministic policy gradient algorithm ［J］. Journal of Liaoning Technical University （Natural Science）， 2020， 39（6）：545-549.）

[12] HOU Y N， LIU L F， WEI Q， et al. A novel DDPG method with prioritized experience replay ［C］// Proceedings of the 2017 IEEE International Conference on Systems， Man， and Cybernetics. Piscataway： IEEE， 2017：316-321.

[13] NIAN R， LIU J F， HUANG B. A review on reinforcement learning： Introduction and applications in industrial process control ［J］. Computers and Chemical Engineering， 2020， 139： Article No.106886.

[14] 李云龙，唐文俊，白成海，等.青霉素生产工艺优化及代谢分析提高产量［J］.中国抗生素杂志，2019，44（6）：679-686.（LI Y L， TANG W J，BAI C H， et al. Optimization of the feeding process and metabolism analysis to improve the yield of penicillin ［J］. Chinese Journal of Antibiotics， 2019， 44（6）： 679-686.）

[15] 王蕾，陈进东，潘丰.引力搜索算法在青霉素发酵模型参数估计中的应用［J］.计算机应用，2013，33（11）：3296-3299，3304.（WANG L， CHEN J D， PAN F. Applications of gravitational search algorithm in parameters estimation of penicillin fermentation process model ［J］. Journal of Computer Applications， 2013， 33（11）： 3296-3299， 3304.）

[16] 叶凌箭，程江华.基于Matlab/Simulink的青霉素发酵过程仿真平台［J］.系统仿真学报，2015，27（3）：515-520.（YE L J， CHENG J H. Simulation platform of penicillin fermentation process based on Matlab/Simulink ［J］. Journal of System Simulation， 2015， 27（3）： 515-520.）

Industrial process control method based on local policy interaction exploration-based deep deterministic policy gradient

DENG Shaobin1，2，3，4，ZHU Jun1，2，3， ZHOU Xiaofeng1，2，3*， LI Shuai1，2，3，4， LIU Shurui1，2，3

（1.Key Laboratory of Networked Control System，Chinese Academy of Sciences，Shenyang Liaoning110016，China；2.Shenyang Institute of Automation，Chinese Academy of Sciences，Shenyang Liaoning110169，China；3.Institutes for Robotics and Intelligent Manufacturing Innovation，Chinese Academy of Sciences，Shenyang Liaoning110169，China；4.University of Chinese Academy of Sciences，Beijing100049，China）

In order to achieve the stable and precise control of industrial processes with non-linearity， hysteresis， and strong coupling， a new control method based on Local Policy Interaction Exploration-based Deep Deterministic Policy Gradient （LPIE-DDPG） was proposed for the continuous control of deep reinforcement learning. Firstly， the Deep Deterministic Policy Gradient （DDPG） algorithm was used as the control strategy to greatly reduce the phenomena of overshoot and oscillation in the control process. At the same time，the control strategy of original controller was used as the local strategy for searching， and interactive exploration was used as the rule for learning， thereby improving the learning efficiency and stability. Finally， a penicillin fermentation process simulation platform was built under the framework of Gym and the experiments were carried out. Simulation results show that， compared with DDPG， the proposed LPIE-DDPG improves the convergence efficiency by 27.3%； compared with Proportion-Integration-Differentiation （PID）， the proposed LPIE-DDPG has fewer overshoot and oscillation phenomena on temperature control effect， and has the penicillin concentration increased by 3.8% in yield. In conclusion， the proposed method can effectively improve the training efficiency and improve the stability of industrial process control.

industrial process control; deep reinforcement learning; Deep Deterministic Policy Gradient (DDPG); Local Policy Interaction Exploration (LPIE); penicillin fermentation process

TP273.2

A

1001-9081（2022）05-1642-07

10.11772/j.issn.1001-9081.2021050716

2021⁃05⁃07；

2021⁃09⁃27；

2021⁃11⁃26。

辽宁省“兴辽英才计划”项目（XLYC1808009）。

邓绍斌（1997—），男，江西赣州人，硕士研究生，主要研究方向：强化学习、工业过程控制； 朱军（1964—），男，辽宁沈阳人，研究员，硕士，主要研究方向：自动控制、工业自动化； 周晓锋（1978—），女，辽宁本溪人，副研究员，博士，主要研究方向：机器学习、工业过程优化； 李帅（1988—）男，辽宁锦州人，副研究员，博士研究生，主要研究方向：机器学习、数据挖掘； 刘舒锐（1993—）男，湖北襄阳人，助理研究员，硕士，主要研究方向：工业过程建模与控制、机器学习。

This work is partially supported by Program of Liaoning Province “Xingliao Talents Plan” （XLYC1808009）.

DENG Shaobin， born in 1997， M. S. candidate. His research interests include reinforcement learning，industrial process control.

ZHU Jun， born in 1964， M. S.， research follow. His research interests include automatic control， industrial automation.

ZHOU Xiaofeng， born in 1978， Ph. D.， associate research fellow. Her research interests include machine learning， industrial process optimization.

LI Shuai， born in 1988， Ph. D. candidate， associate research fellow. His research interests include machine learning， data mining.

LIU Shurui， born in 1993， M. S.， assistant research fellow. His research interests include industrial process modeling and control， machine learning.