基于改进遗传算法和图神经网络的股市波动预测方法

李晓寒，贾华丁，程雪，李太勇

（西南财经大学 经济信息工程学院，成都 611130）（∗通信作者电子邮箱lixiaohan134@163.com）

基于改进遗传算法和图神经网络的股市波动预测方法

李晓寒*，贾华丁，程雪，李太勇

（西南财经大学 经济信息工程学院，成都 611130）（∗通信作者电子邮箱lixiaohan134@163.com）

针对支持向量机（SVM）、长短期记忆（LSTM）网络等智能算法在股市波动预测过程中股票评价特征选择困难及时序关系维度特征缺失的问题，为能够准确预测股票波动、有效防范金融市场风险，提出了一种基于改进遗传算法（IGA）和图神经网络（GNN）的股市波动预测方法——IGA-GNN。首先，利用相邻交易日间的时序关系构建股市交易指标图数据；其次，通过评价指标特性优化交叉、变异概率来改进遗传算法（GA），从而实现节点特征选择；然后，建立图数据的边与节点特征的权重矩阵；最后，运用GNN进行图数据节点的聚合与分类，实现了股市波动预测。在实验阶段，所研究的股票总评价指标数为130个，其中IGA在GNN方法下提取的有效评价指标87个，使指标数量降低了33.08%。应用所提IGA在智能算法中进行特征提取，得到的算法与未进行特征提取的智能算法相比，预测准确率整体提升了7.38个百分点；而与应用传统GA进行智能算法的特征提取相比，应用所提IGA进行智能算法的特征提取的总训练时间缩短了17.97%。其中，IGA-GNN方法的预测准确率最高，相较未进行特征提取的GNN方法的预测准确率整体提高了19.62个百分点；而该方法与用传统GA进行特征提取的GNN方法相比，训练时间平均缩短了15.97%。实验结果表明，所提方法可对股票特征进行有效提取，预测效果较好。

股市预测；遗传算法；图神经网络；机器学习；特征选择

0 引言

股票价格走势是一种非线性、非稳定的时间序列，在过去三十多年里，为能够有效防范金融风险，对股票价格的分析和预测从未停止过。实际上，关于股票价格预测的研究发展历程与信息技术的迭代息息相关，最早的股价预测研究可以追溯到20世纪末，Lo等［1］证明了股票价格并不会遵循非随机漫步理论，从而佐证了股市价格的可预测性。随着计算机技术的发展，对于股市价格波动的预测从最初的人工逐渐转变为计算机算法：Dierks等［2］采用遗传算法通过历史交易数据实现了对股票价格趋势的捕捉；Kim等［3］提出了支持向量机（Support Vector Machine， SVM）用于股票价格的研究，后续又进一步利用多层感知器研究股票价格的波动［4］。自此之后，越来越多的智能算法被应用到股市价格波动的研究中。Nelson等［5］以历史交易数据和技术分析指标为基础运用长短期记忆（Long Short-Term Memory， LSTM）网络来预测股价波动趋势。基于卷积神经网络（Convolutional Neural Network， CNN）［6-7］、循环神经网络（Recurrent Neural Network， RNN）等神经网络及其改进神经网络的算法在股票价格波动研究领域得到了广泛的应用［8-9］。特征选择是影响智能算法预测性能的重要因素，上述智能算法输入不同的特征指标，呈现出了不同的预测结果。目前股票市场具有多个维度上万种股票特征因子用于预测和评价股票。为解决股票评价特征选择问题，Huang等［10］和He等［11］提出了通过遗传算法进行特征选择，并与智能算法结合预测股市波动；然而所选用的传统遗传算法忽略了评价特征的时间序列特点，特征选择效率较低。如何高效选择用于智能算法的股市评价特征成为亟待解决的问题。过往研究对于已选定的特征指标数据侧重于单个交易日。为获取股市波动趋势信息，Selvin等［7］提出了应用滑动窗口方法［12］来预测短期内的股市波动，但是其忽略了不同交易间隔中变化的相关性。如何有效捕获及准确表示时间序列特征因子的动态趋势也是需要研究和解决的问题。

为能够准确获取股票特征因子及变化趋势信息，本文提出了基于改进遗传算法（Improved Genetic Algorithm， IGA）和图神经网络（Graph Neural Network， GNN）的股市波动预测方法IGA-GNN进行股票特征因子的选择，通过遗传算法（Genetic Algorithm， GA）进行全局搜索，应对量化特征因子的评价选择［13］，并引入自适应交叉概率和变异概率提高全局搜索效率［14］。同时，构建了股票特征图数据，每个交易日为一个节点，将经过选择的特征因子设置为节点特征，相邻交易日设置为节点的边，相邻交易日的特征因子变动量设置为边权重，运用图神经网络对构建的图数据分析预测股市波动。

1 相关工作

1.1 股市预测

股票市场的研究中已经证明，股价趋势预测与金融时间序列的特征密切相关［1］。事实上，金融数据之间具有噪声、非线性、随机的金融时间特征，影响因素众多且复杂［15］。但是Edwards等［16］研究证明金融时间序列走势会重现，个别特殊时间序列走势会极其相似地出现在未来时间序列的走势中。因此，股票价格走势可以被预测，学者们引入各种评价指标，用于股市价格波动的预测。从最初的开盘价、收盘价等直接指标逐渐衍生出动能、重量等有效显示某一特性的间接指标，如：Jegadeesh等［17］提出了股票的价格有延续原来的运动方向的趋势，成交量、换手率均衍生出动量因子用于股票价格走势预测；Fama等［18］利用总市值、账面市值比等衍生指标因子构建了因子定价模型用于解释预期股票报酬率的横截面变化。随着评价指标研究的更新变化，股市预测方法也在不断发展。预测方法从最初的人工通过交易数据进行预测逐渐转变为通过计算机获得的金融时间序列统计特性辅助预测，例如，ARMA（Auto Regressive Moving Average）等方法就是基于时序的统计学特性进行股票价格预测［19］。随着人工智能的飞速发展，股票走势预测逐渐由机器辅助预测转变为计算机可自主迭代学习预测。经典的机器学习算法如SVM、LSTM等广泛应用于股票价格走势预测［20］，但始终存在引言中所述的问题需要进一步探索。

1.2 遗传算法

Holland教授基于优胜劣汰的生物进化理论于1975年提出了遗传算法［21］，遗传算法具有简单易于实现，且具有普遍适用性的特点。在之后的几十年中遗传算法在各个领域得到了广泛应用［22-24］，并且随着算法应用的深入，遗传算法不断得到优化改进［25-26］。金融预测方面遗传算法也得到了广泛应用，如：1）对于智能算法的参数优化，Kim等［27］提出了一种基于遗传算法的特征离散化方法，优化神经网络层间的连接权值和特征离散化的阈值降低特征空间维度，预测股票价格指数；Fang等［28］提出了改进遗传算法优化目标和小波神经网络变化的网络参数以改善神经网络在股市预测中的表现。2）对于时间窗口的优化，Chung等［29］运用现有财务数据建立了长短期记忆网络和遗传算法融合的股票市场预测模型，利用遗传算法来确定长短期记忆网络的时间窗大小及拓扑结构，通过实验选择韩国股票价格指数验证了所提方法的预测准确率优于基准模型。采用遗传算法进行特征选择及权重优化，Bonde等［30］取得了上市公司的6个属性，并使用6个连接权重进行连接，每个连接权重值定义了每个属性在预测股票价格时给出的贡献，运用遗传算法优化连接权重用于量化分析公司股票波动。但是，遗传算法对于股票评价特征选择的维度较少，且对于多维特征选择的效率也并不理想。

1.3 图神经网络

为能够解决图数据的深度学习问题，图神经网络应运而生。短短几年时间图神经网络技术突飞猛进，得到了广泛的应用［31］。Bruna等［32］首次提出了图卷积神经网络，采用谱空间方法定义图卷积。ChebNet（Chebyshev Net）［33］和图神经网络（GNN）［34］为能够降低时空复杂度，从空间角度定义节点的权重矩阵，对核函数进行参数优化。近年来，部分金融领域学者也尝试使用关系数据进行金融领域研究，并提出了运用此类方法预测股市波动。Kim等［35］提出了一种利用关系数据进行股票市场预测的分层注意力网络，用于预测个股价格和市场指数的走势；Liu等［36］提出了一种利用上市公司之间各种关系知识图谱并采用门控循环单元（Gated Recurrent Unit， GRU）的模型用于股市波动预测；Matsunaga等［37］研究了市场预测和图神经网络交叉工作的有效性；Chan［38］则通过构建相关公司关系图的方式采用图卷积神经网络方法进行信息融合分析。虽然学者们针对利用图神经网络方法对股市预测进行了研究探索，但是仍处于起步阶段。对于金融图数据关系维度的表示及应用，特别是股市评价特征的图数据并未有更为深入的探究。

总结以上研究的局限性，主要有以下几个方面：1）首先，遗传算法对于机器学习算法在股市预测方面的优化，多基于对算法参数的优化，而非立足于股市金融属性本身对股市评价特征因子进行相关优化及搜索。2）其次，面对海量股市评价特征因子进行选择，以往的研究多以静态截面数据为主，而忽略了特征因子波动趋势信息，特征节点信息与趋势信息未能较好实现融合。3）另外，传统的机器学习算法缺乏对金融市场波动维度的分析，忽略了股市波动的趋势规律及延续性，主要以欧几里得结构样本进行数据训练及预测，对于股市波动趋势传导机制有待进一步探索。

为了克服现有相关工作的局限性，本文提出了一种基于改进遗传算法和图神经网络的股市波动预测方法，通过提高交叉及变异效率改进遗传算法进行股市评价特征因子的选择，构建包含特征因子波动趋势信息的股市评价图数据，并运用图神经网络方法预测股市波动情况。本文的主要工作如下：

1）解决股市评价特征因子预测股市波动的过拟合问题，利用因子间的相关性更新变异概率优化遗传算法完成股市特征因子选择。

2）以交易日为节点构建股市图数据，创新股市评价特征嵌入方法，以此捕获传递股市趋势信息。

3）鉴于图神经网络对于非欧氏数据处理的优势［39］，本文从图神经网络边的消息传递角度，结合构建的股市图数据特点优化图神经网络的消息传递机制，对股市波动进行预测。

2 本文方法

2.1 模型的整体设计

本文所提出的方法通过改进遗传算法选择股票特征因子构建图数据，并运用图神经网络进行股市波动的预测，模型框架如图1所示，通过接口获取Yahoo财经数据，加工生成股市评价因子。

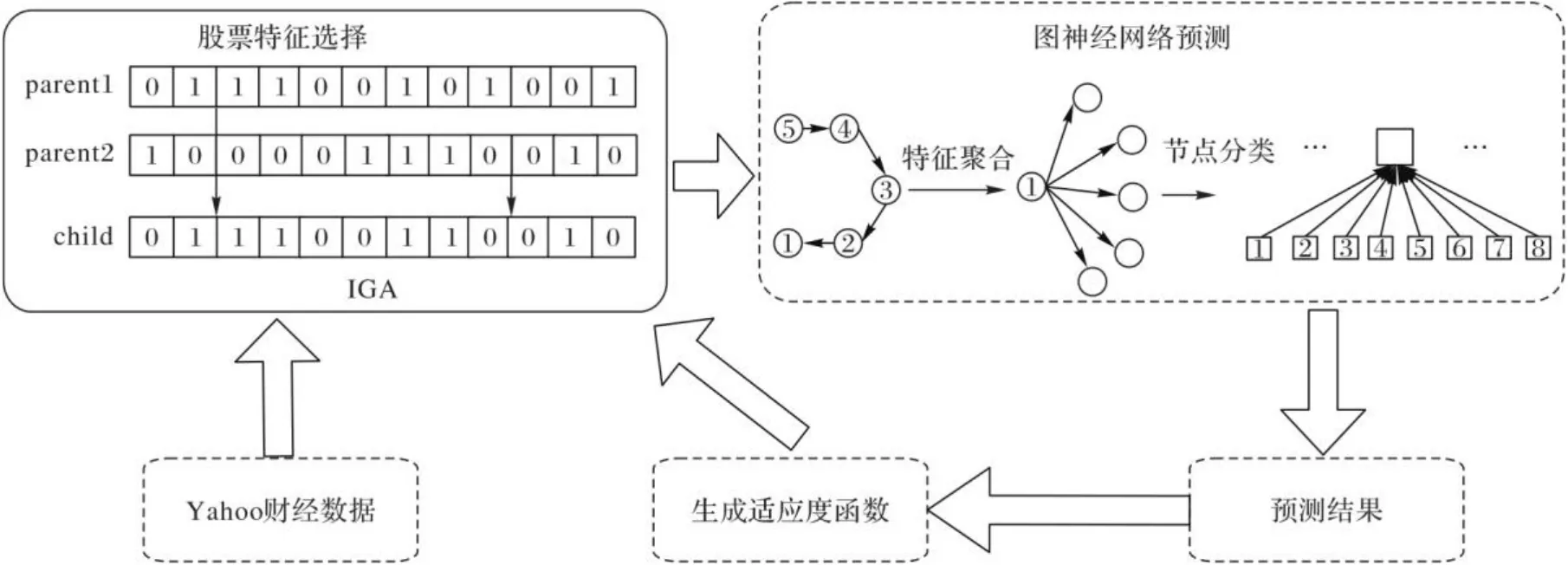
图1 本文模型框架示意图Fig. 1 Schematic diagram of proposed model framework

如图1所示，模型对所要进行选择的因子进行基因编码，并采用改进遗传算法进行全局搜索。本文所提出的IGA的核心为根据股票特征因子的特性动态调整交叉概率和变异概率，以提高GA的效率，避免陷入局部最优。将经选择后的股市评价特征因子用于构建预测股市的图数据，采用图神经网络对图数据节点聚合，以股市涨跌为标记进行节点分类。将量化评价预测准确率作为适应度函数的输出对本文IGA进行迭代优化。最终，得到有效评价股票的特征因子用于股市波动预测，如图2所示。

2.2 图数据构建

本文中选取较为常用的13个股票评价特征指标数据表示为一个二进制向量：。表示第个指标是否用于评价股票，表示第个指标不用于评价预测股票，表示第个指标用于评价预测股票。本文参考文献［16-17］中提及的指标参数，进行了指标参数的合并归纳，本文采用的13个股票指标数据如表1所示，包括：最高价（High price， High）、最低价（Low price， Low）、开盘价（Opening price， Open）、成交量（Volume of transaction， Volume）、复权后的收盘价（Closing price， Close）、简单移动平均值（simple Moving Average， MA）、指数移动平均值（Exponential Moving Average， EMA）、顺势指标（Commodity Channel Index， CCI）、动量指标（MoMenTum， MMT）、动量指标%K（StOchastic K%， SOK）、动能指标%D（StOchastic D%， SOD）、强力指数（Force Index， FI）、重量指数（Mass Index， MI）。在取以上指标参数的基础上，赋予不同的时间跨度（3 d，5 d，10 d和15 d）。

2.3 改进遗传算法

遗传算法是根据生物进化理论衍生出来的搜索最优解的方法，其核心是“适者生存”的理念，通过不停地迭代个体和种群，完成优胜劣汰。本文将量化投资收益作为一个种群适应度，每一个量化投资策略作为一个个体，股票特征因子则作为染色体，染色体将会通过不同的机器学习算法带来盈利，种群个体在迭代进化过程中，算法采用交叉、变异等遗传操作实现最优个体及染色体的选择。寻找最优股票特征因子作为机器学习的训练资源，达到最优适应度，实现量化投资策略收益的最大化。

2.3.1 染色体编码的设置

染色体编码是遗传算法优化机器学习算法的关键，本文选取2.2节中介绍的较为常用的13个股票指标数据作为染色体基因，包括最高价、最低价、开盘价、成交量、复权后的收盘价、简单移动平均值、指数移动平均值、顺势指标、动能指标、动能指标%K、动能指标%D、强力指数、重量指数。

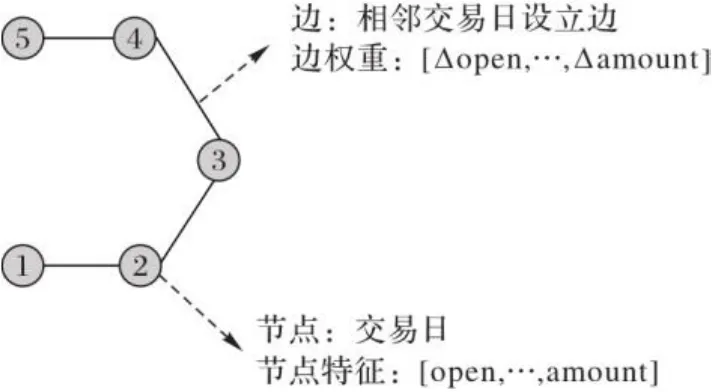
图2 股市评价特征因子Fig. 2 Feature factors of stock market evaluation

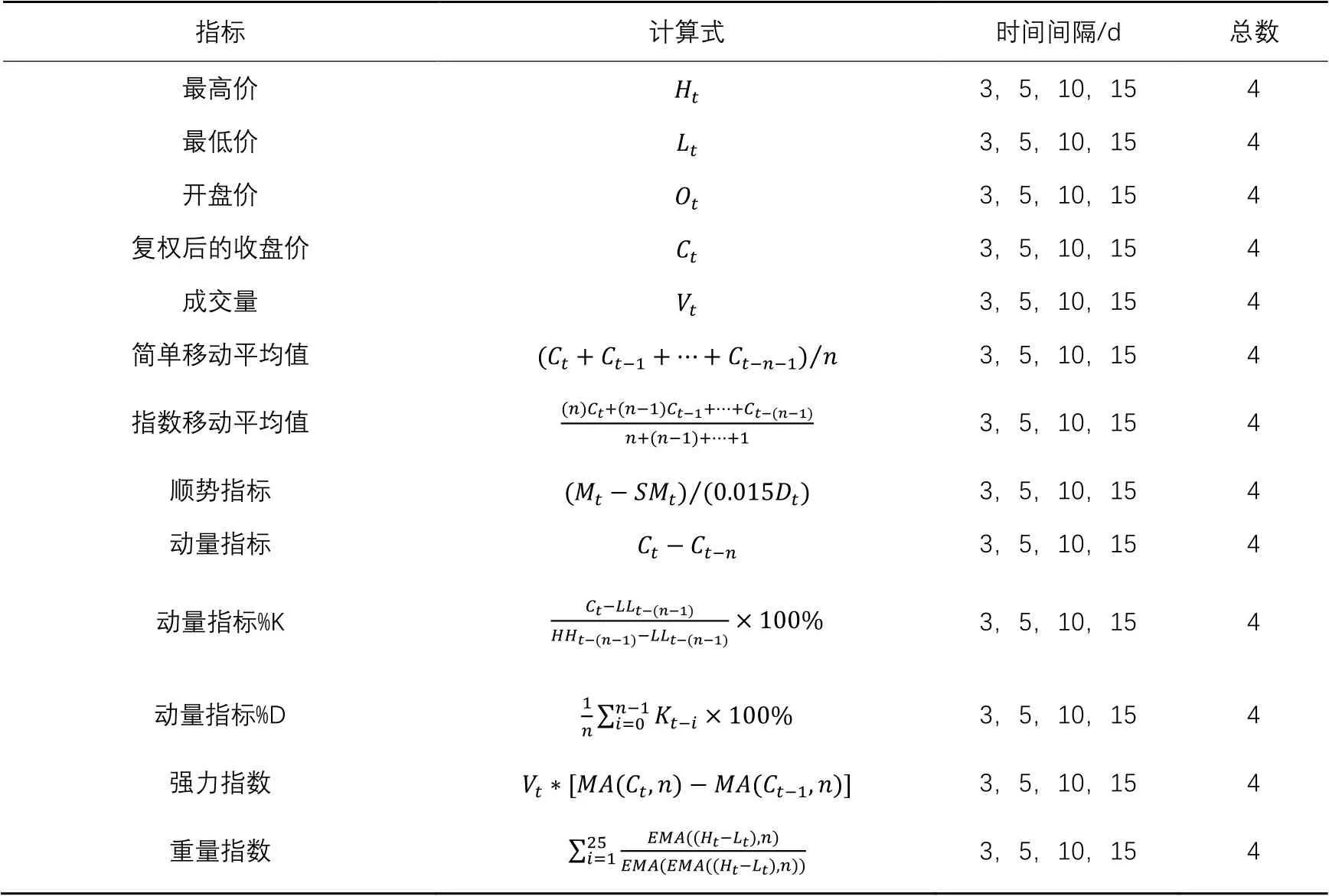
表1 常用的股票指标参数Tab. 1 Common stock index parameters

2.3.2 适应度函数的确定

机器学习模型的准确率是评价机器学习预测模型的重要指标，模型的准确率与预测性能密切相关。个体适应度则为算法的最终追求目标，也是算法迭代的动力，设为适应度函数，机器学习的混淆矩阵如表2所示。

表2 混淆矩阵Tab. 2 Confusion matrix

个体的适应度函数为：

机器学习的准确率为遗传算法不断进化的目标，机器学习的预测准确率越高，个体表现越好，其个体及种群的适应度就越大。

2.3.3 遗传操作的设计

传统选择算子常采用轮盘赌法或最优个体保存策略，采用传统方法选择算子会把适应度高的个体淘汰，或者出现局部最优现象，降低了遗传进化效率。设是种群中个体的个数，是的适应度，采用轮盘法选出的个体的概率依赖于种群向量，概率表达式为：

由大数定理可知，大样本平均值与单个实验结果的期望值接近。随着种群数量不断变多，选择每一个个体的比例会接近于。

具体流程为：初始化种群，计算种群内个体的适应度，将个体适应度按照最优进行排序，如果，即种群中个体适应度大于上一个种群中个体适应度中的最大值，则作为精英个体进行保留，剩余个体按照式（3）给出的随时间、适应度值及初始向量变化的比例向量实施选择动作。

2.3.4 自适应交叉概率和变异概率的设计

通过实验验证可知，传统遗传算法对于不同应用场景并未表现出高效的普适性，结合各个领域、应用场景的改进遗传算法应运而生。改进遗传算法多采用自适应的方式调整交叉概率。适应度好的，赋予一个较小的交叉概率，而且随着迭代不断增加，赋予的交叉概率不断减小。引入这种自适应的交叉概率策略以提高GA的全局搜索能力。

本文基于现有研究［40］（如表3所示）的基础上，对交叉和变异概率进行了重新设计，交叉概率设计如下：

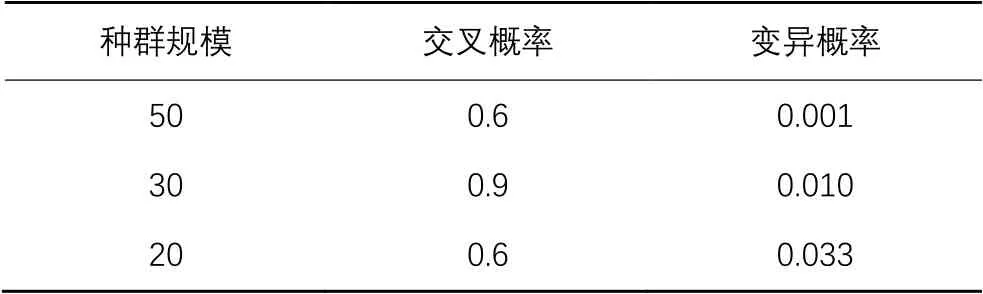
表3 遗传算法的参数设置Tab. 3 Parameter setting of genetic algorithm

本文IGA部分中个体基因是股票特征因子，其之间存在相关关系，变异概率不采用固定值，基因突变是保持物种多样的必要操作，因此选择个体基因之间相关系数的平均值作为变异概率，相关系数平均值越大，变异概率越大。为了避免导致近亲繁殖和进入进化的死胡同，根据式（7）求得各基因之间的相关系数，形成相关系数矩阵。

不同个体结合相关系数矩阵，可以获得基因之间的相关系数平均值，则变异概率设计如下：

2.4 优化图神经网络

本文借鉴GraphSAGE（Graph Sample and AggreGatE）嵌入生成方法［41］，对于股市评价特征因子图数据指标均采用消息传递模式进行相应指标子图的节点更新嵌入。基于图神经网络进行股市波动预测的流程如图3所示。

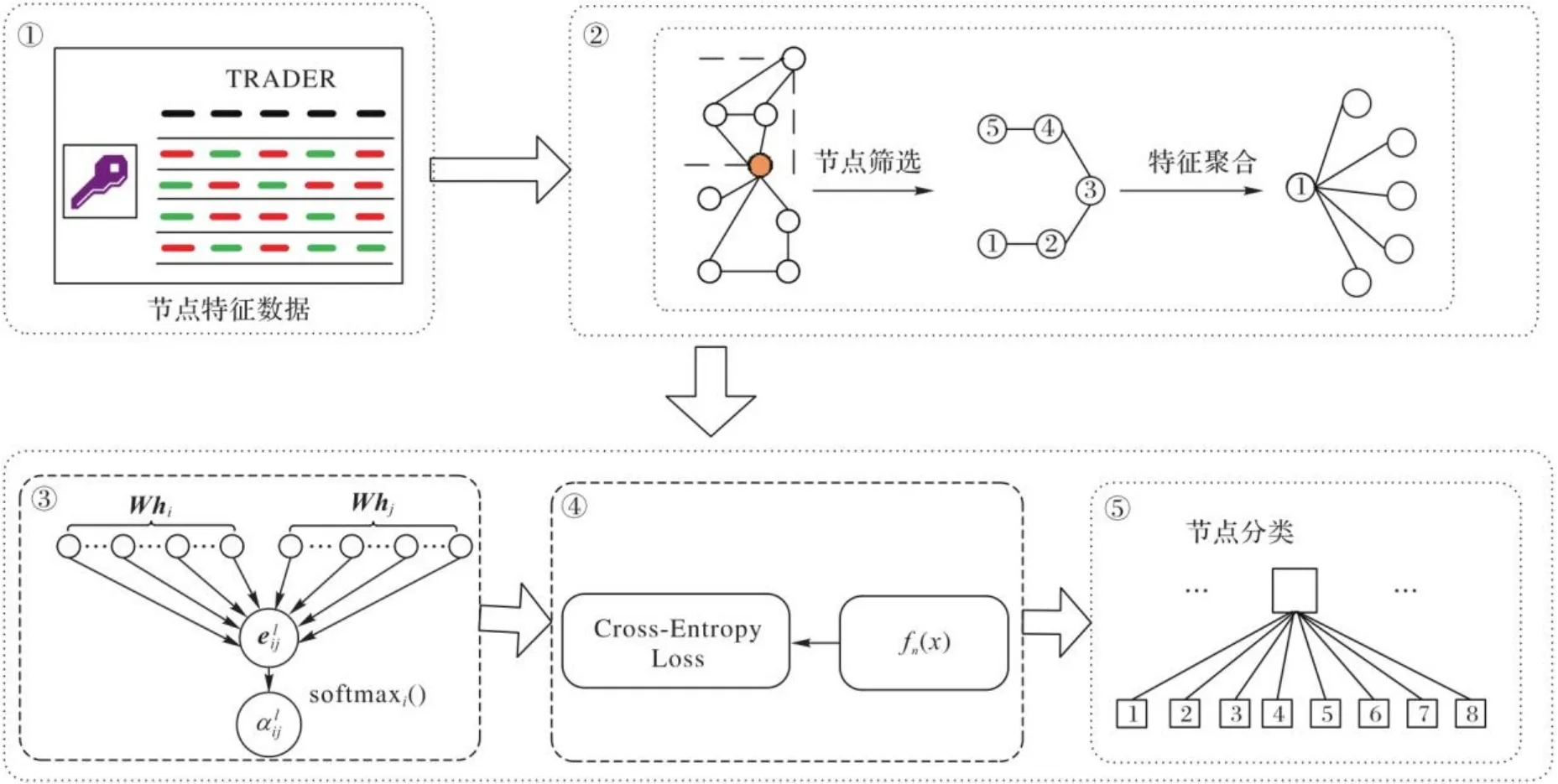
图3 基于图神经网络股市波动预测流程Fig. 3 Flow chart of stock market volatility prediction based on graph neural network

3 实验验证与结果分析

本文数据来源于雅虎财经2000年1月1日至2019年6月15日苹果（AAPL）、脸书（FB）、特斯拉（TSLA）、通用汽车（GM）、国际商业机器公司（IBM）、微软（MSFT）、卡特彼勒（CAT）、埃克森美孚（XOM）、家得宝（HD）、标普500ETF-SPDR（SPY）的指标数据，包括最高价、最低价、开盘价、成交量、复权后的收盘价、移动平均值、指数移动平均值、顺势指标、动量指标、动量指标%K、动量指标%D、强力指标、重量指数，指标构建方式如表1所示。其中，2000年1月1日至2015年12月31日为训练数据，2016年1月1日至2019年6月15日为测试数据。采用标准普尔500指数中的500支成分股进行训练，为能有效测量准确率和收益，采用标准普尔500指数基金进行回测。实验在Intel Xeon Silver4114 CPU RAM 128 GB的服务器上运行完成，软件环境为Python3.6.1。

为能够进一步验证所构建模型的优越性，本文将IGA应用在K最近邻（K-Nearest Neighbor， KNN）分类算法、支持向量机（SVM）算法、长短期记忆（LSTM）网络算法、朴素贝叶斯（Naive Bayesian， NB）算法进行比较。将实验数据按交易日指标数据和波动值组成向量进行其他算法的训练及测试。

KNN算法的理论来源于极限定理，样本的分类主要根据其最近邻的一个或几个样本来决定待分类样本的所属类别。KNN算法更加适合类域的交叉和重叠较多的样本集。

支持向量机（SVM）是一种应用广泛的机器学习分类算法，将特征指标拼接成向量，并将向量输入支持向量机进行预测。

长短期记忆（LSTM）网络在1997年被首次提出，是为了解决RNN存在的问题，避免梯度消失和爆炸。该算法将原来简单的神经网络结构改造为链式结构，通过门结构实现对信息的控制、保护和传递。

朴素贝叶斯（NB）理论是基于贝叶斯定理和特征条件独立假设。朴素贝叶斯算法属于监督机器学习，其核心是基于概率进行分类，概率值则取决于待分类客体的设定特征。用于对比的模型参数设置参考文献［42-45］，如表4所示，其中GNN参数为式（9）～（11）中的变量，指标因子为13个，且图数据中的边为无向边，所以GNN参数设置为。

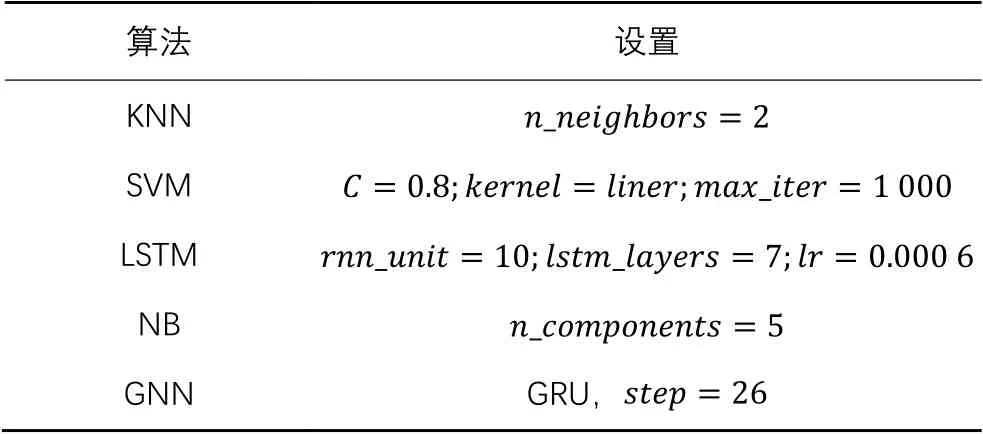
表4 不同算法参数设置Tab. 4 Parameter setting of different algorithms

3.1 模型训练效率

将各经典机器学习算法采用GA和本文IGA的训练时间进行比较，通过图神经网络采用不同的遗传算法策略进行特征选择，图4以苹果公司股票（AAPL）为例展示了特征选择遗传算法的进化过程，同时给出了自适应交叉和变异概率过程，GA为基本遗传算法［46］，IGA1为改进算法采用固定的交叉变异算子进行优化［40］，IGA2为采用了交叉变异算子自调整策略［47］，IGA3为采用了本文提出的改进遗传算法。

图4 不同改进遗传算法的进化过程Fig. 4 Evolution processes of improved genetic algorithms

训练时间的对比结果如表5所示，从表5中可以看出：采用本文提出的IGA进行机器学习的训练速度优于采用传统GA进行特征选择机器学习的训练速度，本文所提的IGA相较于传统GA在特征选择效率方面更有优势。传统GA应用于实验中智能算法进行特征提取的总训练时间为1 520 126 s，本文IGA用于该过程的总训练时间为1 246 886 s，总训练时间缩短了17.97%。其中，IGA有效提升了图神经网络的训练效率，IGA-GNN相较使用GA的图神经网络的训练时间平均缩短了15.97%。

3.2 模型预测性能

表6中，经过本文IGA优化的机器学习算法提高了股市预测精度。实验结果表明，对于遗传算法所选择出的股票评价特征，不同股票和机器学习算法所选择的最优特征体系是不同的，进一步验证了采用本文IGA进行特征选择的必要性，每支股票和机器学习算法通过适配提取出的因子最大限度提高了预测准确率和效率。

表7则给出了改进遗传算法在图神经网络方法下选择的最优评价股票因子。表7中涉及个股10支，总评价指标数130个，结果显示有效指标87个，指标数量下降了33.08%。下文将按照表7所示特征因子体系进行策略回测，验证策略的收益。

表5 不同算法的训练时间对比 单位： sTab. 5 Comparison of training time among different algorithms unit： s

表6 不同算法的准确率对比Tab. 6 Comparison of accuracy among different algorithms

表7 IGA-GNN方法选择的股票评价指标Tab. 7 Stock evaluation indexes selected by IGA- GNN method

3.3 收益情况比较

本文选取2020年6月1日至2020年12月31日的150个交易日的数据进行文本策略的回测。模型预测上涨，则生成买入信号，下降则生成卖出信号，连续相同信号不触发交易操作。策略初始资金为10 000，以交易日收盘价作为收益结算标准。根据表6中的预测准确率，选取IGA-KNN、IGA-SVM、IGA-LSTM、IGA-NB、GNN与本文方法进行比较。图5给出了本文所提方法形成的策略在投资苹果、脸书、特斯拉、通用汽车、国际商业机器公司、微软、卡特彼勒、埃克森美孚、家得宝、标普500ETF-SPDR（AAPL、FB、TSLA、GM、IBM、MSFT、CAT、XOM、HD、SPY）的所得收益情况。

由表6～7可以初步得出，不同的股票及算法对于股票评价特征体系具有不同的要求，但是在几支股票中，特征指标均选择了重量指数、移动平均值和复权后的收盘价。移动平均值能够反映股票价格变化的惯性指标，惯性的特质使其可以作为判断股市走势的有效工具，其波峰、波谷及形态则可以提供量化交易中进行交易的有效信号。复权后的收盘价为每日最终股票状态。两种重要指标也是量化策略经常采用的指标，如金叉死叉策略等。可以看出，本文提出的改进遗传算法具有较好的评价股票特征指标选择的能力。采用该方法进行特征选择的算法的预测准确率优于传统采用全维度特征的算法。

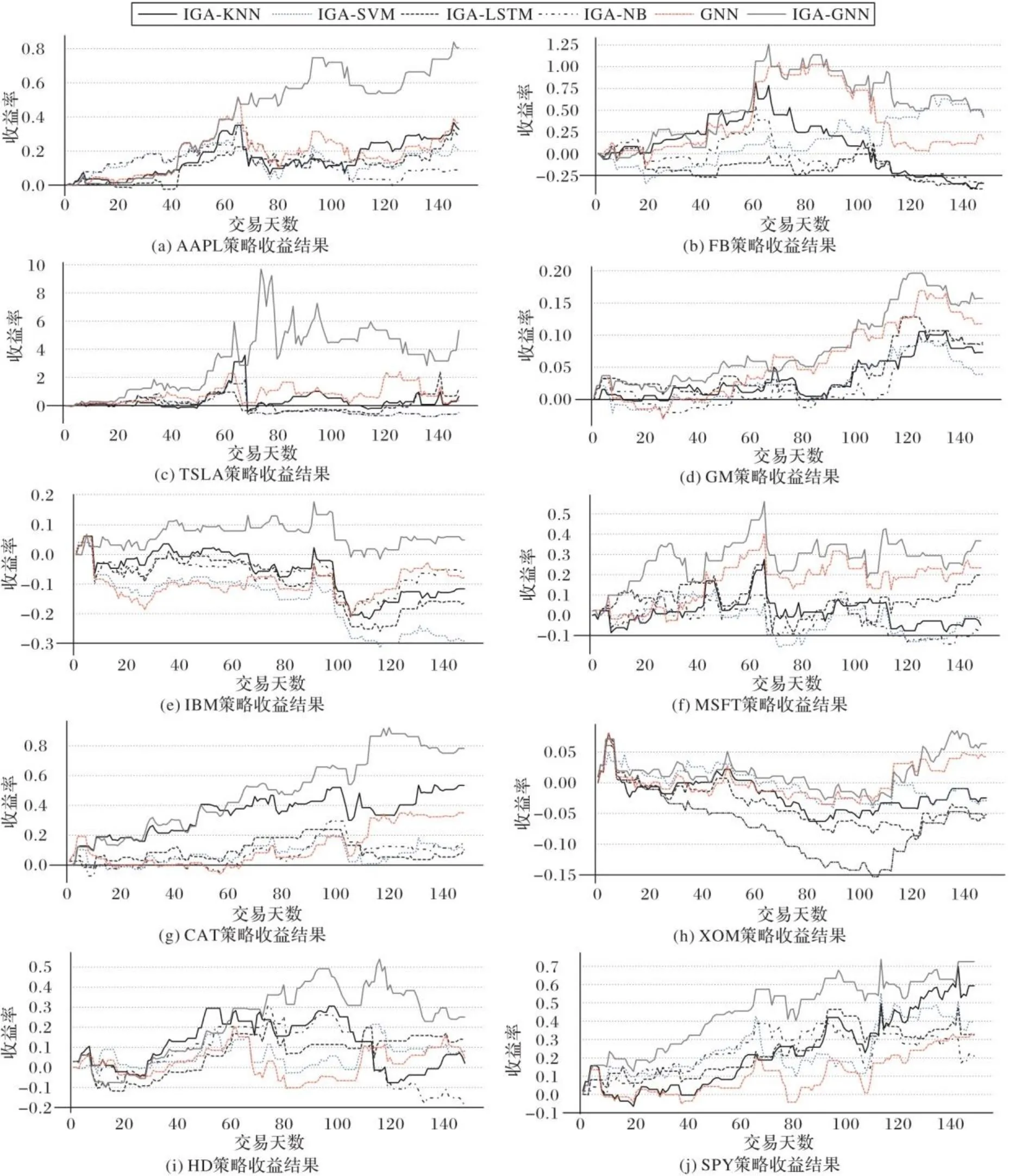
图5 不同算法的量化策略投资收益情况Fig. 5 Investment returns of quantitative strategies in different algorithms

如图5中个股及标准普尔500指数策略收益结果所示，IGA-GNN形成的策略交易收益最优，与表6中呈现的结果基本相符。股市交易指标图数据嵌入和图神经网络预测方法的准确率与经过本文IGA进行特征选择后的LSTM、KNN、SVM、LSTM、NB方法准确率相当，甚至略优于以上方法。表6结果表明本文所提基于改进遗传算法和图神经网络的预测方法远优于未经过该方法进行特征选择的方法，验证了本文所提出的IGA有效提升了智能算法的预测性能。将节点特征作为图数据的核心组成部分，图5给出了经过本文改进遗传算法特征选择的图神经网络IGA-GNN具有更好的预测性能，明显优于GNN方法，进一步验证了改进遗传算法特征选择对于图神经网络的重要性。然而，图5（h）中对于XOM个股的GNN与IGA-GNN方法的策略收益最为接近，经表7的特征选择结果分析可知，采用本文改进遗传算法进行特征选择的方法经训练优化后，最优评价指标中并未选择重量指数（Mass Index）。XOM个股波动的预测最优评价指标维度与全量维度最为接近，进一步验证了特征选择的有效性。综上，实验结果充分验证了本文改进遗传算法与图神经网络方法融合的必要性和优越性。

4 结语

目前主流的机器学习算法广泛应用于量化投资领域，由于机器学习算法存在面对海量的数据和瞬息万变的市场行情算法训练时间过长的问题，模型迭代更新速度严重影响预测准确率，本文提出了IGA-GNN方法以自适应交叉概率和变异概率的方式改进GA，使其作为选择特征的核心，并运用图神经网络方法进行股票评价预测。本文方法在提高股票特征因子使用效率的同时，保证了所选择股票特征因子的可解释性，通过实验验证了本文方法有效提高了股市波动预测准确率。但是，本文采用的评价指标为股票交易数据，而实际金融市场中影响股票波动的因素非常多，对于股票多源异构信息的融合及分析将成为下一步研究的方向。

[1] LO A W， MACKINLAY A C. Stock market prices do not follow random walks：evidence from a simple specification test ［J］. The Review of Financial Studies， 1988， 1（1）： 41-66.

[2] DIERKS T， ALLEN C. The TLS protocol version 1.0： RFC 2246［S］. Reston： Internet Society， 1999.

[3] KIM K. Financial time series forecasting using support vector machines ［J］. Neurocomputing， 2003， 55（1/2）： 307-319.

[4] 邓一沙.多层感知器神经网络构建交易策略——基于沪深300股指期货数据［D］.成都：西南财经大学，2012：62-71.（DENG Y S. Building a trading strategy via multilayer perceptron neural network — base on the CSI300Stock index futures data ［D］. Chengdu：Southwestern University of Finance and Economics， 2012： 62-71.）

[5] NELSON D M Q， PEREIRA A C M， DE OLIVEIRA R A. Stock market’s price movement prediction with LSTM neural networks ［C］// Proceedings of 2017 International Joint Conference on Neural Networks. Piscataway： IEEE，2017： 1419-1426.

[6] WHITE H. Economic prediction using neural networks： the case of IBM daily stock returns ［C］// Proceedings of the IEEE 1988 International Conference on Neural Networks. Piscataway： IEEE， 1988：451-458.

[7] SELVIN S， VINAYAKUMAR R， GOPALAKRISHNAN E A， et al. Stock price prediction using LSTM， RNN and CNN-sliding window model ［C］// Proceedings of the 2017 International Conference on Advances in Computing，Communications and Informatics. Piscataway： IEEE， 2017： 1643-1647.

[8] RATHER A M， AGARWAL A， SASTRY V N. Recurrent neural network and a hybrid model for prediction of stock returns ［J］. Expert Systems with Applications， 2015， 42（6）： 3234-3241.

[9] JAHAN I， SAJAL S. Stock price prediction using Recurrent Neural Network （RNN） algorithm on time-series data ［EB/OL］. ［2021-01-12］. http：//micsymposium.org/mics2018/proceedings/MICS_2018_paper_55.pdf.

[10] HUANG C F， CHANG B R， CHENG D W， et al. Feature selection and parameter optimization of a fuzzy-based stock selection model using genetic algorithms ［J］. International Journal of Fuzzy Systems， 2012，14（1）：65-75.

[11] HE Y Q， FATALIYEV K， WANG L P. Feature selection for stock market analysis ［C］// Proceedings of the 2013 International Conference on Neural Information Processing， LNCS 8227. Berlin： Springer， 2013： 737-744.

[12] CHOU J S， NGUYEN T K. Forward forecast of stock price using sliding-window metaheuristic-optimized machine-learning regression ［J］. IEEE Transactions on Industrial Informatics， 2018， 14（7）： 3132-3142.

[13] BARON M， BROGAARD J， HAGSTRÖMER B， et al. Risk and return in high-frequency trading ［J］. Journal of Financial and Quantitative Analysis， 2019， 54（3）： 993-1024.

[14] BERAT SEZER O， OZBAYOGLU A M. Algorithmic financial trading with deep convolutional neural networks： time series to image conversion approach ［J］. Applied Soft Computing， 2018， 70： 525-538.

[15] 李立辉，田翔，杨海东，等.基于SVR的金融时间序列预测［J］.计算机工程与应用，2005，41（30）：221-224.（LI L H，TIAN X， YANG H D， et al. Financial time series forecasting based on SVR ［J］. Computer Engineering and Applications，2005， 41（30）： 221-224.）

[16] EDWARDS R D， MAGEE J， BASSETTI W H C. Technical Analysis of Stock Trends ［M］. 11th ed. Boca Raton： CRC Press， 2018：34-45.

[17] JEGADEESH N， TITMAN S. Returns to buying winners and selling losers：implications for stock market efficiency ［J］. The Journal of Finance， 1993， 48（1）： 65-91.

[18] FAMA E F， FRENCH K R. Common risk factors in the returns on stocks and bonds ［J］. Journal of Financial Economics， 1993， 33（1）： 3-56.

[19] TANG H， CHIU K C， XU L. Finite mixture of ARMA-GARCH model for stock price prediction ［EB/OL］. ［2021-03-10］. http：//www.cse.cuhk.edu.hk/～lxu/papers/conf-chapters/TangCIEF2003.pdf.

[20] CHEN K， ZHOU Y， DAI F Y. A LSTM-based method for stock returns prediction： a case study of China stock market ［C］// Proceeding of 2015 IEEE International Conference on Big Data. Piscataway： IEEE， 2015： 2823-2824.

[21] 李敏强，寇纪淞，林丹，等.遗传算法的基本理论与应用［M］.北京：科学出版社，2002：31-62.（LI M Q， KOU J S， LIN D， et al. Basic Theory and Application of Genetic Algorithm ［M］. Beijing： Science Press， 2002： 31-62.）

[22] 李壮年，储满生，柳政根，等.基于机器学习和遗传算法的高炉参数预测与优化［J］.东北大学学报（自然科学版），2020，41（9）：1262-1267.（LI Z N， CHU M S， LIU Z G， et al. Prediction and optimization of blast furnace parameters based on machine learning and genetic algorithm ［J］. Journal of Northeastern University （Natural Science）， 2020， 41（9）： 1262-1267.）

[23] SILVA R C C， DE MENEZES JÚNIOR J M P， DE ARAÚJO JÚNIOR J M. Optimization of NARX neural models using PSO and GA algorithms applied to identification of photovoltaic systems ［J］. Journal of Solar Energy Engineering， 2021， 143（5）： Article No. 051001.

[24] 孙波，姜平，周根荣，等.改进遗传算法在移动机器人路径规划中的应用［J］.计算机工程与应用，2019，55（17）：162-168.（SUN B， JIANG P， ZHOU G R， et al. Application of improved genetic algorithm in path planning of mobile robots ［J］. Computer Engineering and Applications，2019， 55（17）： 162-168.）

[25] WHITLEY D， STARKWEATHER T. GENITOR II： a distributed genetic algorithm ［J］. Journal of Experimental and Theoretical Artificial Intelligence， 1990，2（3）： 189-214.

[26] JIAO L C， WANG L. A novel genetic algorithm based on immunity［J］. IEEE Transactions on Systems， Man， and Cybernetics — Part A： Systems and Humans， 2000， 30（5）： 552-561.

[27] KIM K J， HAN I. Genetic algorithms approach to feature discretization in artificial neural networks for the prediction of stock price index ［J］. Expert Systems with Applications， 2000， 19（2）： 125-132.

[28] FANG Y， FATALIYEV K， WANG L P， et al. Improving the genetic-algorithm-optimized wavelet neural network for stock market prediction ［C］// Proceeding of the 2014 International Joint Conference on Neural Networks. Piscataway： IEEE， 2014： 3038-3042.

[29] CHUNG H， SHIN K S. Genetic algorithm-optimized long short-term memory network for stock market prediction ［J］. Sustainability，2018， 10（10）： Article No.3765.

[30] BONDE G， KHALED R. Stock price prediction using genetic algorithms and evolution strategies ［EB/OL］. ［2021-02-10］. http：//worldcomp-proceedings.com/proc/p2012/GEM4716.pdf.

[31] 呼延康，樊鑫，余乐天，等.图神经网络回归的人脸超分辨率重建［J］.软件学报，2018，29（4）：914-925.（HU Y K， FAN X， YU L T， et al. Graph based neural network regression strategy for facial image super-resolution ［J］. Journal of Software， 2018， 29（4）： 914-925.）

[32] BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral networks and locally connected networks on graphs ［EB/OL］. ［2021-02-12］. http：//arxiv.org/pdf/1312.6203.pdf.

[33] DEFFERRARD M， BRESSON X， VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering ［C］// Proceedings of the 2016 30th International Conference on Neural Information Processing Systems. Red Hook： Curran Associates Inc.， 2016：3844-3852.

[34] KIPF T N， WELLING M. Semi-supervised classification with graph convolutional networks ［EB/OL］. ［2021-02-12］. https：//arxiv.org/pdf/1609.02907.pdf.

[35] KIM R， SO C H， JEONG M， et al. HATS： a hierarchical graph attention network for stock movement prediction ［EB/OL］. ［2021-02-12］. https：//arxiv.org/pdf/1908.07999.pdf.

[36] LIU J， LU Z C， DU W. Combining enterprise knowledge graph and news sentiment analysis for stock price volatility prediction ［EB/OL］. ［2021-02-10］. https：//scholarspace.manoa.hawaii.edu/bitstream/10125/59565/1/0125.pdf.

[37] MATSUNAGA D， SUZUMURA T， TAKAHASHI T. Exploring graph neural networks for stock market predictions with rolling window analysis ［EB/OL］. ［2021-02-12］. https：//arxiv.org/pdf/1909.10660.pdf.

[38] CHAN W S. Stock price reaction to news and no-news： drift and reversal after headlines ［J］. Journal of Financial Economics， 2003， 70（2）： 223-260.

[39] BRONSTEIN M M， BRUNA J， LECUN Y， et al. Geometric deep learning： going beyond Euclidean data ［J］. IEEE Signal Processing Magazine， 2017， 34（4）： 18-42.

[40] DE JONG K A， SPEARS W M， GORDON D F. Using genetic algorithms for concept learning ［J］. Machine Learning， 1993， 13（2/3）： 161-188.

[41] HAMILTON W L， YING R， LESKOVEC J. Inductive representation learning on large graphs ［C］// Proceedings of the 2017 31st International Conference on Neural Information Processing Systems. Red Hook： Curran Associates Inc.， 2017： 1025-1035.

[42] CHEN Y J， HAO Y T. A feature weighted support vector machine andK-nearest neighbor algorithm for stock market indices prediction ［J］. Expert Systems with Applications， 2017， 80：340-355.

[43] LI Q， JIANG L L， LI P， et al. Tensor-based learning for predicting stock movements ［C］// Proceedings of the 2015 29th AAAI Conference on Artificial Intelligence. Palo Alto： AAAI Press， 2015： 1784-1790.

[44] LIU X W， DOU Y， YIN J P， et al. Multiple kernelk-means clustering with matrix-induced regularization ［C］// Proceedings of the 2016 30th AAAI Conference on Artificial Intelligence. Palo Alto： AAAI Press， 2016： 1888-1894.

[45] SHIHAVUDDIN A S M， AMBIA M N， AREFIN M M N， et al. Prediction of stock price analyzing the online financial news using Naive Bayes classifier and local economic trends ［C］// Proceedings of the 2010 3rd International Conference on Advanced Computer Theory and Engineering. Piscataway： IEEE， 2010： V4-22-V4-26.

[46] VOSE M D. The Simple Genetic Algorithm： Foundations and Theory ［M］. Cambridge： MIT Press， 1999： 89-95.

[47] JAFAR-ZANJANI S， INAMPUDI S， MOSALLAEI H. Adaptive genetic algorithm for optical metasurfaces design ［J］. Scientific Reports， 2018， 8： Article No.11040.

Stock market volatility prediction method based on improved genetic algorithm and graph neural network

LI Xiaohan*， JIA Huading，CHENG Xue， LI Taiyong

（School of Economic Information Engineering，Southwestern University of Finance and Economics，Chengdu Sichuan611130，China）

Aiming at the difficulty in selecting stock valuation features and the lack of time series relational dimension features during the prediction of stock market volatility by intelligent algorithms such as Support Vector Machine （SVM） and Long Short-Term Memory （LSTM） network， in order to accurately predict stock volatility and effectively prevent financial market risks， a new stock market volatility prediction method based on Improved Genetic Algorithm （IGA） and Graph Neural Network （GNN）named IGA-GNN was proposed. Firstly， the data of stock market trading index graph was constructed based on the time series relation between adjacent trading days. Secondly， the characteristics of evaluation indexes were used to improve Genetic Algorithm （GA） by optimizing crossover and mutation probabilities， thereby realizing the node feature selection. Then， the weight matrix of edge and node features of graph data was established. Finally， the GNN was used for the aggregation and classification of graph data nodes， and the stock market volatility prediction was realized. In the experiment stage， the studied number of total evaluation indexes of stock was 130， and 87 effective evaluation indexes were extracted from the above by IGA under GNN method， making the number of stock evaluation indexes reduced by 33.08%. The proposed IGA was applied to the intelligent algorithms for feature extraction. The obtained algorithms has the overall prediction accuracy improved by 7.38 percentage points compared with the intelligent algorithms without feature extraction. Compared with applying the traditional GA for feature extraction of the intelligent algorithms， applying the proposed IGA for feature extraction of the intelligent algorithms has the total training time shortened by 17.97%. Among them， the prediction accuracy of IGA-GNN method is the highest， which is 19.62 percentage points higher than that of GNN method without feature extraction. Compared with the GNN method applying the traditional GA for feature extraction， the IGA-GNN method has the training time shortened by 15.97% on average. Experimental results show that， the proposed method can effectively extract stock features and has good prediction effect.

stock market prediction; Genetic Algorithm (GA); Graph Neural Network (GNN); machine learning; feature selection

TP391.7

A

1001-9081（2022）05-1624-10

10.11772/j.issn.1001-9081.2021030519

2021⁃04⁃06；

2021⁃07⁃15；

2021⁃07⁃15。

中央高校基本科研业务费专项资金资助项目（JBK2102001）。

李晓寒（1985—），男，山东济南人，博士研究生，CCF会员，主要研究方向：金融信息管理、智能决策、大数据、商务智能； 贾华丁（1956—），男，四川成都人，教授，博士，CCF会员，主要研究方向：机器学习、算法交易、扩频序列设计； 程雪（1997—），女，山西河津人，硕士研究生，CCF会员，主要研究方向：机器学习、量化交易； 李太勇（1979—），男，四川安岳人，教授，博士，CCF高级会员，主要研究方向：机器学习、模式识别、自然计算。

This work is partially supported by Fundamental Research Funds for Central Universities （JBK2102001）.

LI Xiaohan， born in 1985， Ph. D. candidate. His research interests include financial information management， intelligent decision-making， big data， business intelligence.

JIA Huading， born in 1956， Ph. D.， professor. His research interests include machine learning， algorithmic trading， spread spectrum sequence design.

CHENG Xue， born in 1997， M. S. candidate. Her research interests include machine learning，quantitative trading.

LI Taiyong， born in 1979， Ph. D.， professor. His research interests include machine learning， pattern recognition， natural computing.