基于信号处理和深度学习的牛顿环实验

鲁溟峰,武进敏,杨文明，张 峰,陶 然

(1.北京理工大学 信息与电子学院，北京 100081；2.北京信息科技大学 自动化学院，北京 100101；3.上海交通大学 物理与天文学院，上海 200240)

牛顿环实验是大学物理的基础实验，它面向全校理工科开设，受众很广. 实验利用牛顿环干涉条纹测量平凸透镜的曲率半径，研究等厚干涉现象. 图1为牛顿环实验的示意图，将曲率半径很大的平凸透镜放在玻璃板上，使凸面与平板玻璃接触，形成空气劈尖. 用单色光垂直照射，经空气劈尖的上下表面反射得到2束相干光，相干光叠加形成牛顿环干涉条纹. 通过第k级暗环的半径rk可求得平凸透镜的曲率半径为

(1)

图1 牛顿环实验(等厚干涉)

为了使学生能够较好地观察牛顿环，完成曲率半径的测量，可以在传统牛顿环实验仪的基础上增加摄像头(CCD/CMOS)采集整幅牛顿环图像到计算机中，利用数字图像处理软件处理牛顿环，完成曲率半径测量. 例如，利用Matlab软件对牛顿环图的环心和条纹半径/直径进行测量[1-2]，再依据相关公式计算得到曲率半径；或采用数据处理软件(Origin，Excel，Matlab，Python等)进行最小二乘法拟合[3-4]. 这种基于数字图像的数环法较传统数环法更为方便，无回程误差，观测视场范围大. 除此之外，也可利用高级图像处理方法来测量牛顿环的环心、半径/直径，实现一定程度的自动测量. 例如，利用图像灰度阈值化、图像极值跟踪法、梯度矢量场等相关方法提取牛顿环的骨架线(条纹中心线)[5-7]，利用Hough变换及衍生方法检测牛顿环的环心[8-10]，进行各环定级和测量各级圆环的直径/半径，再根据相关公式计算得到平凸透镜的曲率半径. 另外，也有采用线性回归等数据处理方法来获取环心位置和半径/直径[11-12]，或者利用圆内接三角形的思路来获得相关参量[13-14]，增加了测量的便捷性.

以上方法是把基于肉眼的传统数环改为基于数字图像的数环，是针对传统数环法的升级和补充，方法繁琐、鲁棒性差、自动化程度不高，并且这些图像处理方法与牛顿环成像机理及信号本质无太大关系，也不适合纳入大学物理教学中. 本文从2个新的视角来观测牛顿环，分别是基于信号处理和深度学习的牛顿环干涉条纹分析，无需数环，即可对牛顿环进行自动分析，测量平凸透镜的曲率半径和牛顿环的环心，为牛顿环实验提供了具有创新性和实用性的扩展实验手段.

1 牛顿环的信号处理

对于等间隔条纹，可以用傅里叶变换(Fourier transform，FT)来处理，但是对于牛顿环这类非等间隔的闭合干涉条纹，其表征无论是在空域还是在傅里叶域都过于复杂(图2)，很难直接进行分析[15].

(a)空域 (b)傅里叶域图2 牛顿环的空域、傅里叶域

目前，Victor Nascov等人根据牛顿环的信号特性，采用最小二乘法、转动惯量法和傅里叶法对牛顿环进行了分析[16-18]，这些方法虽脱离了数环法的框架，但操作步骤繁琐复杂，测量的精度和鲁棒性也不尽人意.

1.1 牛顿环是Chirp信号

如图1所示，单色光垂直照射被测件和平板玻璃，在空气劈尖的上下表面反射形成2束相干光，其光程差为

(2)

根据光程差,可得2束光之间的相位差为

(3)

根据光波叠加原理，频率相同、振动方向相同、相位差恒定的2束光在某点相遇叠加后，形成稳定的干涉条纹，其叠加后的平均光强为

(4)

其中I1,I2为2束反射光的光强，它们近似一致，可用Ic表示，代入式(4)，联立式(3)，可得

(5)

I(x,y)=2Ic+2Iccos (πKx2-2πKx0x+

(6)

由式(6)可知牛顿环的干涉条纹是二次相位信号，其每行/列都和雷达通信中常用的Chirp信号形式一致，其信号本质是二维Chirp信号[19]，如图3所示.

图3 牛顿环条纹的信号本质

1.2 基于分数傅里叶变换的牛顿环处理

在电子信息领域，Chirp信号处理工具非常丰富，包括分数傅里叶变换(Fractional Fourier transform，FRFT)、Chirp傅里叶变换(Chirp-Fourier transform， CFT)、Chirplet变换、菲涅耳变换等. 本文从牛顿环的信号本质出发，来分析干涉条纹，在分数傅里叶域观测牛顿环，获得被测件的曲率半径等物理参量. 其中，FRFT的定义式为

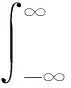
(7)

式中，α为时频平面旋转的角度，Kα(u,x)=Bαexp [jπ(u2cotα-2uxcscα+x2cotα)]为核函数.

基于牛顿环的任何行/列都可表示为Chirp信号，取其中1行为例，其简化的复指数形式可写为Ir(x)=Aexp (jπKx2-j2πKx0x+jφy)，利用FRFT分析，可得冲激函数

(K+cotα)x2]}dx.

(8)

当cotα=-K时，此时α为匹配旋转角，代入式(8)，计算得到

Iαr(u)=Aαyδ(Kx0+ucscα).

(9)

基于以上分析，本文开发了牛顿环信号分析软件用于物理实验教学，从成像信号的角度来观测牛顿环，该方法原理简单、无需数环，利用积分公式即可计算出结果. 由于该方法充分挖掘了信号特征，因此测量的精度和鲁棒性较好. 另外，该信号分析软件还可以让学生在信号视角下观测牛顿环. 学生在理解FRFT积分的基础上，调试参量，观测牛顿环在分数傅里叶域的能量聚集性，测量曲率半径.

1.3 基于Chirp傅里叶变换的牛顿环处理

分数傅里叶变换(FRFT)、Chirp傅里叶变换(CFT)为普通傅里叶变换(FT)的广义形式，FT适合处理正弦信号，而FRFT和CFT适合处理Chirp信号，信号经过变换会形成冲激信号. CFT是FRFT的简化形式，其离散形式更适合数值计算[20-21]. 其中，CFT的定义为

(10)

式中，k为频率，l为线性调频率.当l固定时，对I(x)的Chirp傅里叶变换就变为对I(x)exp (-jlx2)的傅里叶变换.当l=0时，Chirp傅里叶变换就是傅里叶变换.

与分数傅里叶域分析牛顿环过程类似，牛顿环的任何行/列都可表示为Chirp信号，以其中1行为例，其简化的复指数形式可写为

Ir(x)=Ayexp [j(β0x2+α0x)],

(11)

其中，α0=-2Kπx0,β0=Kπ分别为待估计行信号的频率和调频率.使用CFT处理Ir(x)，计算得到

Ay2πδ(k-α0).

(12)

在Chirp傅里叶域中通过搜索峰值，得到α0和β0，进而推导出牛顿环条纹的曲率半径Rrow=2π/(λ0β0)和圆心横坐标x0=-α0/(2β0).同理，对列信号做类似处理，也可以得到列曲率半径Rcol和圆心坐标y0.最后通过对计算得到的行和列信号的半径求均值，得到待测平凸透镜的曲率半径和牛顿环的环心坐标(x0,y0).

CFT比FRFT具有更简明的公式形式，因此更适合进行数值计算，但是这种简化导致CFT不具备FRFT的光学特性，例如在近代物理光学领域中，FRFT经常用来描述光的衍射，CFT则无法描述.

2 牛顿环的深度学习

近年来，深度学习已被各行各业广泛应用，并取得了良好的效果. 但大部分应用是对图像进行分类，诸如对人脸分类，而如何从图像中获取参量的应用属于深度学习的拟合问题，相对分类任务更难. 图4为采用深度卷积神经网络实现牛顿环参量端到端的估计[22-24]. 神经网络采用的VGG卷积神经网络，是2014年牛津大学计算机视觉组和Google DeepMind公司共同研发出的深度卷积神经网络(Visual Geometry Group Network，VGGNet)[25]，由5层卷积层、3层全连接层以及softmax输出层构成. 本文基于该网络架构进行改进，设计了适合牛顿环参量估计的改进VGG网络结构，网络共11层，包含10个卷积层和1层全连接，如图5所示. 其中卷积层采用3×3大小的卷积核，其激活函数为ReLU，用这样的结构来提取牛顿环中的特征；最大池化用于减少特征图的尺寸、冗余的信息和网络参量；非线性激活函数ReLU代替原来的softmax，用来保持网络的非线性拟合能力，并在网络的输出层设置3个神经元，即环心坐标(x0,y0)和曲率半径R.

图4 基于卷积神经网络的牛顿环直接参量估计

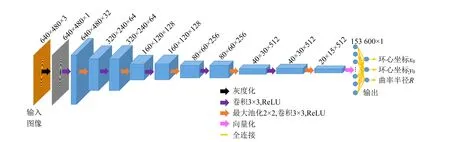
图5 改进VGG网络结构用于牛顿环分析

基于该科研成果，开发了适合牛顿环实验的深度学习实验平台，训练和测试流程基于tensorflow的keras框架，在英伟达Quardro RTX 5000的GPU上进行，如图6～7所示.

图6 深度神经网络训练流程

图7 深度神经网络分析牛顿环结果

1)数据集准备.

120 000张尺寸为640×480的仿真牛顿环. 这些图像以10∶1的比例分为了训练集和测试集，每张图都有标注环心坐标和曲率半径. 另外，利用牛顿环实验仪采集1 500张真实的牛顿环条纹图作为训练集.

2)训练.

损失函数：均方误差函数；

Adam优化器：起始的学习率为0.001，动量更新的参量为0.9和0.999；

批量梯度下降：batchsize为16；

分批训练：12 000张/批.

3)测试验证.

a. 仿真理想牛顿环：曲率半径相对偏差为0.01%～0.05%，环心误差≤1 pixel；

b. 仿真均匀光照牛顿环：

高斯噪声(信噪比为25～-5 dB)：曲率半径相对偏差为0.01%～0.18%，环心误差≤1 pixel；

椒盐噪声(噪声密度为0～60)：曲率半径相对偏差为0.01%～0.23%，环心误差≤1 pixel；

c. 仿真非均匀光照牛顿环：

高斯噪声(信噪比为25～-5 dB)：曲率半径相对偏差为0.02%～0.35%，环心误差≤1 pixel；

椒盐噪声(噪声密度为0～60)：曲率半径相对偏差为0.02%～0.25%，环心误差≤1 pixel；

d. 实测牛顿环：曲率半径相对估计误差<0.62%，环心误差≤1 pixel，单张(640×480)测试时间约为0.01 s.

3 教学效果

3.1 具有创新启发性

基于信号处理和深度学习的牛顿环实验不拘泥于传统的数环法，而是从2个新颖的角度观测牛顿环. 该实验可以作为数环法实验的补充，以扩展传统教学思路，具有较好的创新性和启发性. 通过牛顿环干涉条纹在分数傅里叶变换域的能量聚集性，深刻理解牛顿环干涉成像的机理和数学本质. 通过大数据训练深度神经网络，使其具有分析牛顿环的智能性，帮助学生理解牛顿环的数据特征，激发学生对干涉现象的深入思考，培养学生的创新精神，拓宽学生的视野.

3.2 具有知识拓展性和通用性

基于信号处理和深度学习的牛顿环实验是对传统等厚干涉实验的良好补充，在完成传统基础实验后，通过拓展实验完成新视角下的牛顿环观测，扩展新知识，可以支撑大学物理、信号处理、人工智能等多学科课程乃至大创和竞赛.

3.2.1 基础实验(面向理工科专业)

实验名称：基于数环法分析的透镜曲率半径测量(4学时).

实验目的：理解牛顿环等厚干涉成像原理，掌握基本光路的搭建和调试，了解visio画圆.

实验原理：牛顿环本质上属于等厚干涉，由1块曲率半径较大的平凸透镜放在光学平板玻璃上构成，平板玻璃表面与凸透镜球面之间形成楔形的空气间隙. 当用单色光照射牛顿环仪时，在球面与平玻璃接触点周围形成同心圆干涉环——牛顿环. 如果已知入射光波长λ，测得第k级暗环直径Dk，则可求得透镜曲率半径R.

实验步骤：

1) 根据透、反射式牛顿环实验光路示意图搭建光路；

2) 观察、拍摄反射式牛顿环；

3) 定标图像拍摄；

4) 利用visio工具，标定各级圆环，记录相应级数直径，计算曲率半径，完成实验报告.

3.2.2 扩展实验1(面向物理、光学、信息专业)

实验名称：基于分数傅里叶变换(FRFT)的透镜曲率半径测量(4学时).

实验目的：了解牛顿环成像原理并完成光路搭建和调试，理解基于FRFT算法的牛顿环条纹分析原理.

实验原理：将1块曲率半径较大的平凸透镜放在光学平板玻璃上，使其凸面与平面接触，两者之间形成楔形的空气间隙，当用单色平行光照射牛顿环仪时，在球面与平玻璃接触点周围形成同心圆干涉环——牛顿环. 作为傅里叶变换(FT)的一般形式，从信号处理角度出发，FRFT是基于Chirp基函数分解的信号处理工具，从光学传播角度出发，FRFT可以描述光的衍射.

实验步骤：

1) 根据透、反射式牛顿环实验光路示意图搭建光路；

2) 观察、拍摄反射式牛顿环，拍摄定标图像；

3) 理解基于FRFT的牛顿环参量估计原理；

4) 根据实验指导书，熟悉基于FRFT的牛顿环分析软件；

5) 输入所需参量，计算曲率半径，记录结果；

6) 调整输入参量，记录曲率半径测量结果，完成实验报告.

3.2.3 扩展实验2(面向物理、光学、信息专业)

实验名称：基于深度学习的透镜曲率半径测量(4学时).

实验目的：了解牛顿环成像原理并完成光路搭建和调试，理解基于深度学习的牛顿环条纹分析原理.

实验原理：将1块曲率半径较大的平凸透镜放在光学平板玻璃上，使其凸面与平面接触，两者之间形成楔形的空气间隙，当用平行单色光照射牛顿环仪时，在球面与平玻璃接触点周围形成同心圆干涉环——牛顿环. 从数据处理角度出发，深度神经网络是先进的数据分析工具，可以通过训练使神经网络从牛顿环条纹中学习参量.

实验步骤：

1) 根据透、反射式牛顿环实验光路示意图搭建光路；

2) 观察、拍摄反射式牛顿环，拍摄定标图像；

3) 理解基于深度学习的牛顿环参量估计原理；

4) 根据实验指导书，熟悉基于深度学习的牛顿环分析方法；

5) 设置超参量，训练网络，测量曲率半径，记录结果，完成实验报告.

3.3 具有实用性

基于信号处理(FRFT和VGG)的牛顿环实验法比数环法具有更好的精度和鲁棒性，即使在图像被污损的情况下也能保证测量精度，这是由于牛顿环的信号特性和数据特性是数环法及基于数字图像处理后的改进数环法所无法比拟的. 而且，比起Victor Nascov等人提出的最小二乘法、傅里叶法[16-18]，本文介绍的牛顿环实验法测量的精度和鲁棒性更好. 本文仿真不同噪声情况下的牛顿环图(图8)，测试各种方法的鲁棒性，如表1～2所示.

(a)理想情况 (b)均匀光照含高斯噪声

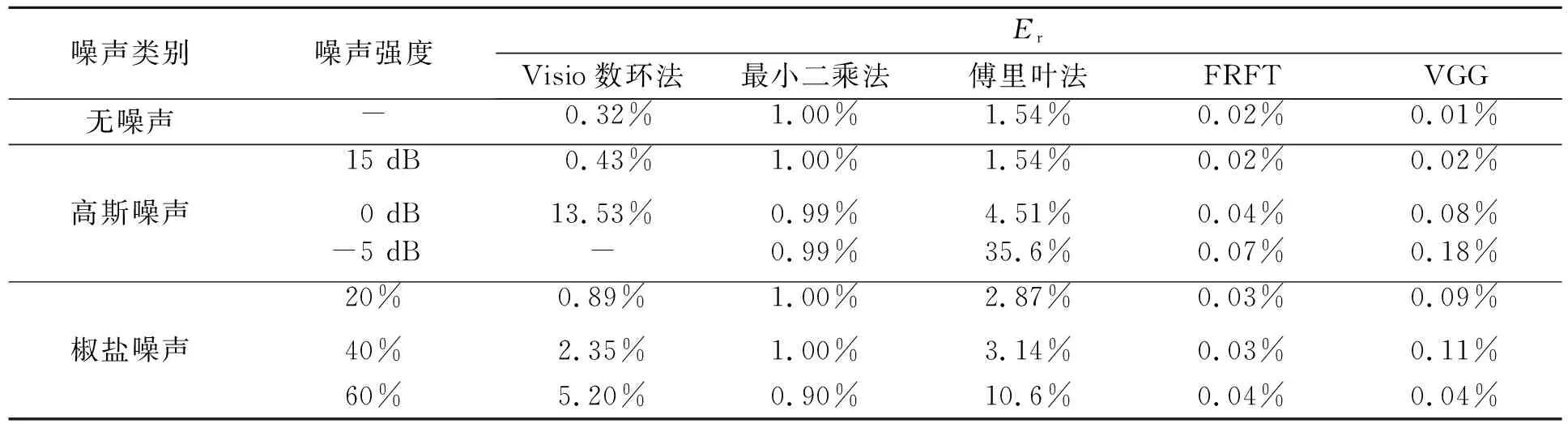
表1 不同方法对均匀光照牛顿环仿真图的曲率半径估计(相对偏差)效果比较

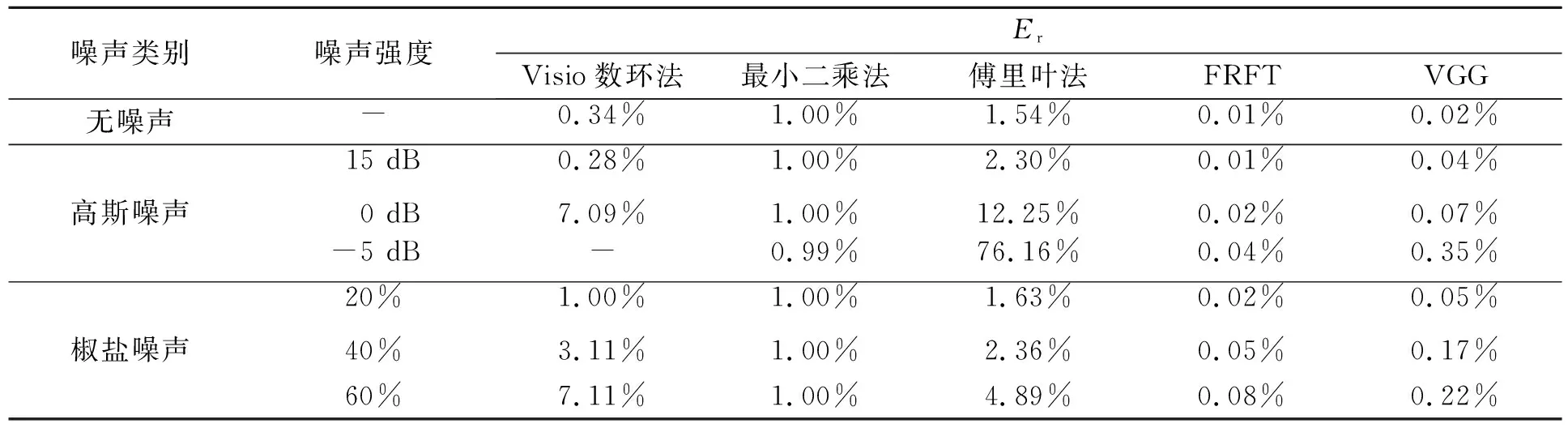
表2 不同方法对非均匀光照牛顿环仿真图的曲率半径估计(相对偏差)效果比较

用大学物理等厚干涉实验仪测量不同曲率半径的平凸透镜(0.855～1.443 m),采集到的真实牛顿环条纹如图9所示，进行各种方法的鲁棒性测试，进一步证实本文介绍的牛顿环实验法的测量精度和鲁棒性更好的结论，如表3所示.

(a) (b)

表3 不同方法对真实牛顿环图像的曲率半径估计(相对偏差)效果比较

基于信号处理和深度学习的实验方法可以完成传统数环法所不能实现的环心定位，在仿真图(640×480)中，FRFT和VGG的环心定位精度≤1 pixel；在实测图(640×480)中，FRFT和VGG环心定位精度≤3 pixel. 无论是信号处理还是深度学习实验法，单张牛顿环图(640×480)的测试时间都在1 s以内，而visio数环则需要10 min左右.

大部分高校采用显微镜观测牛顿环，可以在显微镜上加装电子目镜，实现对牛顿环图像的获取，如图10所示，配上信号处理和深度学习软件就可以实现内容翔实的实验，该实验方案所需装置成本低、易于推广.

图10 电子目镜方案

4 结束语

基于信号处理和深度学习的牛顿环实验是对经典等厚干涉实验的创造性改进，无需数环即可完成曲率半径测量，还可进一步得到牛顿环的环心坐标. 有别于基于数字图像处理的数环法，本文所提出的基于信号处理的方法根据牛顿环干涉信号形成机理，提出牛顿环是具有二次相位的二维Chirp信号，引入FRFT和CFT分析牛顿环；基于深度学习的方法充分挖掘牛顿环的数据特性，采用改进的VGG卷积神经网络分析牛顿环. 该方法将信息技术与传统实验融合，将科学前沿融入教学，在传统等厚干涉实验的基础上进行拓展，不仅满足大学物理实验的教学需求，还可扩展到信号处理、人工智能等信息学科领域的教学中，锻炼学生的综合能力和创新性思维. 此外，该实验方法具有实用性，可以用于球面光学元件的专业测量.