基于金刚石NV色心的量子调控教学实验拓展

赵铮阳，周诗韵

(复旦大学 物理学系，上海 200433)

随着现代半导体行业的快速发展，经典计算机中的晶体管尺寸不断变小，量子效应凸显，影响原有器件的功能. 此外，经典计算在本质上是不可逆的，热耗散难以避免. 在这两方面，基于量子力学原理、通过可逆的幺正量子门进行操作[1]的量子计算机具有明显优势. 同时，由于能对叠加态进行操作，量子计算在算法上具有并行加速的优势，其中典型例子有大数分解算法[2]和量子搜索算法[3]等.

近年来，量子计算相关的量子科技发展迅速，成为新一轮科技革命和产业变革的前沿领域，而量子科技研究相关的人才亟待培养. 为此，复旦大学在本科教学中开设了与量子计算相关的实验课程，能够让学生开拓眼界、了解前沿技术，并在动手实践中综合应用所学的理论知识，从而对量子科技产生更深入的理解.

量子计算实验理论内容丰富，操作难度较大，顺利完成实验并不代表学生真正理解其内涵. 因此，讨论量子计算实验内容的教学设计与拓展十分必要. 本文以国仪量子生产的基于金刚石NV色心的量子计算实验仪为基础开展量子计算教学实验，包含2部分内容：a.学习基础的量子调控，了解量子计算基本知识，如量子比特的初始化、操控和读出等；b.进行实际应用，学生通过实现经典的量子D-J算法，理解量子算法的优越性[4-5]. 基于复旦大学的教学实践，着重讨论该实验的第一部分，即量子调控部分的教学内容与方法.

1 实验原理

1.1 量子计算简介

经典计算机的单比特为|0〉或|1〉，但是量子单比特具有叠加态，可以用|0〉和|1〉进行线性组合，形式为

|ψ〉对应单位球(Bloch球)面上的点(sinθcosφ,sinθsinφ,cosθ)，其中|0〉和|1〉分别沿z轴的正半轴和负半轴，θ为|ψ〉与z轴的夹角，φ为|ψ〉与x轴的夹角.对该量子态|ψ〉进行测量时，将会以概率|a|2测得|0〉，以概率|b|2测得|1〉.

典型的量子二能级系统可以看成量子单比特，比较热门的研究体系有光子体系[6]、量子点[7]、离子阱[8]、超导[9]和金刚石[10]等. 金刚石NV色心是室温、常压下即可进行量子计算的实验体系，适合本科教学，本文使用的是基于金刚石NV色心的量子计算实验仪.

1.2 金刚石NV色心的特性

NV色心是金刚石中的氮-空位点缺陷，指1个氮原子取代了金刚石晶格中的1个碳原子，并与临近的1个空位缺陷相结合形成的结构. NV色心结构中的未成对电子表现出自旋为1的特性. 基态3A2是自旋三重态，由晶格导致的零场劈裂1.19×10-5eV, 对应微波频段(频率为2.87 GHz). 外加磁场进一步使简并的|ms=±1〉 态发生塞曼分裂，在实验室磁场(约1.7 mT)下形成的能级差约为2.1×10-7eV,对应频率为50 MHz.第一激发态中，三重态记作3E，与基态的能级差约为1.95 eV，对应零声子线荧光波长为637 nm. 此外，还有2个单态亚稳态1A1和1E，其寿命分别小于1 ns和250 ns，有实验观察到零声子线为1 042 nm的辐射跃迁[11-12]. NV色心的能级结构如图1所示.

图1 金刚石NV色心的能级结构图

室温下常用的非共振激发方法采用波长为520 nm的绿色激光将NV色心从基态激发到激发态的声子边带. 在室温大气环境，NV色心的零声子线会展宽，难以实现选择性的光学激发[12]. 从激发态回到基态有2种途径：一种途径是辐射跃迁，发出零声子线637 nm的荧光，如图1中红色线所示，该过程满足自旋守恒. 由于声子边带的影响，实际上荧光范围为637～750 nm；另一种途径如图1中虚线所示，是由于自旋-轨道耦合导致的内部交叉弛豫过程. 这种方式的跃迁概率依赖于自旋的状态，是NV色心可以被激光初始化和读出的本质原因. 对于|ms=0〉的自旋态，辐射跃迁为主导，灰色虚线所示的非辐射跃迁概率较低；而|ms=±1〉的自旋态，倾向于通过蓝色虚线所示的内部交叉弛豫，经亚稳态1A1和1E回到|ms=0〉，该过程相当于削弱了荧光强度.由于非辐射跃迁的影响，自旋|ms=0〉和|ms=±1〉的荧光对比度最高可达30%[11-12]. 因此，收集激光作用后的荧光强度，能够反映激光作用前的体系状态. 如果激光持续作用，上述过程将持续进行，|ms=±1〉的自旋态不断翻转到|ms=0〉的自旋态，可以实现高达90%的自旋极化效率[12].

把|ms=0〉和|ms=-1〉的自旋态编码为量子比特|0〉和|1〉，则可认为当激光作用一段时间后，体系被初始化到|0〉态.而施加合适频率的微波，自旋将在|ms=0〉与|ms=-1〉的状态间切换，该过程称为拉比振荡，相当于对量子态施加了量子门操作，从而实现量子调控.同理，把|ms=0〉和|ms=+1〉的自旋态编码为|0〉和|1〉，其结果也是类似的.

1.3 拉比振荡原理

(1)

at=a0eiω0t/2,bt=b0e-iω0t/2.

(2)

在XY平面上施加频率为ω的圆偏振磁场

B=[B1cos (ωt),-B1sin (ωt),0],

(3)

代入初态|ψ0〉=|0〉，可以解出|ψt〉.此时|ψt〉的演化可看成是量子态在Bloch球上既以频率ω0绕着z轴进动，又以频率ω1(ω1=γB1，其中γ为旋磁比)做章动.在t时刻进行测量时，量子态|ψt〉处于|0〉态和|1〉态的概率[13]分别为

(4)

(5)

当满足共振条件ω=ω0时，量子态|ψ〉处于|0〉态和|1〉态的概率分别为

(6)

(7)

共振条件下拉比振荡的物理意义可理解为：|0〉态表示自旋沿z轴向上，|1〉态表示自旋沿z轴向下.当外加频率等于ω的圆偏振磁场B1时，初态|ψ0〉=|0〉随着微波作用的时长t演化到叠加态|ψt〉.对|ψt〉进行测量，测得其处于|0〉态的概率|at|2是时长t的余弦函数，振荡频率δ=ω1，与微波场的大小B1成正比.

2 实验装置

图2所示为国仪量子教学机的光路模块. 520 nm的激光通过透镜会聚在金刚石NV色心上，产生的荧光经过透镜会聚，经滤光片滤掉激光后，被光电探测器收集. 微波装置能够发射频率ω可调的线偏振微波，被微波开关调制成方波脉冲，经功率放大器放大后，通过微波辐射结构作用到金刚石上. 通过电脑软件控制激光和微波的脉冲作用，进行信号采集，并同步时序[5].

(a)实物图

3 实验内容及讨论

3.1 拉比振荡实验

1)施加一段时间的激光，初始化NV色心.

2)打开微波，调节ω和t.拉比振荡实验中，保持ω=ω0不变，调节t；连续波实验中，固定t，调节ω.

3)再次打开激光并进行荧光测量.

在实验中，为了避免不同信号开关的延迟，各脉冲序列间一般会等待5 μs.

图3 拉比振荡和连续波实验脉冲序列图

在准共振频率附近进行拉比振荡实验，其他参量设置为：微波功为率-10 dBm，小磁铁位置为-5.25 cm(出厂位置).实验结果如图4(蓝色数据)所示，对应颜色的实线为拟合结果，拟合公式为y=y0+Ae-t/τcos [δ(t-t0)]，考虑到微波场的不均匀性，加入了e-t/τ项[14-15].

图4 偏共振拉比振荡实验结果

3.2 微波频率对拉比振荡的影响

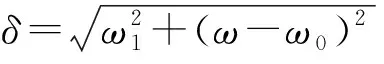
改变ω-ω0，重复拉比振荡实验，可以得到荧光强度随微波作用时间t的变化(以2 848 MHz作用时，荧光光强的最大值和最小值进行归一)，并进行拟合，结果如图4所示.可见微波频率2 848 MHz最接近共振频率，对应的荧光极小值最小.相应地，2 844 MHz和2 840 MHz的拉比振荡频率更高，荧光极小值也更高.

3.3 连续波实验

通过上述讨论可知，只有频率ω=ω0的微波作用后荧光强度最低.从图4中也可以看出，尽管拉比振荡的频率有差异，但荧光取极小值对应的微波时长比较接近.因此，采用“连续波实验”，即连续地改变微波频率测量荧光强度的方法来测量共振频率ω0.

该实验中，荧光信号的测量方法与拉比振荡类似，脉冲序列如图3所示，此时改变微波频率ω，而作用时长t不变(软件中t不可调)，实验结果如图5所示.由于磁场作用，|ms=±1〉的能级去简并，因此荧光强度出现2个低谷，分别为(2 848±2) MHz和(2 896±2) MHz，对应|ms=0〉和|ms=-1〉以及|ms=+1〉之间的共振频率ω0i/(2π)(i=1,2).

图5 连续波实验测量结果

3.4 微波时长对共振频率判断的影响

在连续波实验中，微波的作用时长t不可调.而从图4中可以发现，荧光值随t振荡变化.固定t，将导致所测荧光强度大于等于真实π脉冲下的荧光强度. 下面，讨论这种测量方法对测量ω0的影响.

在ω0=2 848 MHz 附近，每改变0.5 MHz测量1次拉比振荡，并从拉比振荡曲线中读取特定t所对应的荧光强度，做荧光强度与微波频率的关系，如图6(a)所示. 其中t选取2 848 MHz对应的π脉冲时长115 ns，以及(115±25) ns这3个不同的时长. 可以看到，3条曲线的相似度较高，极小值均在(2 846.5±0.5) MHz范围内. 因此，可猜测在实验所测量的荧光强度不确定度范围内，t的选取对共振频率的确定影响不大.

用Mathematica进一步验证上述猜测. 对NV色心的2个共振频率ω0i(i=1,2)，分别考虑微波频率偏离共振频率的影响，根据式(4)，并乘以衰减项e-t/τ，得到相对荧光强度Ii(i=1,2)

(8)

总荧光强度

I=I1+I2-1.

(9)

将ω01/(2π)=2 846.5 MHz，ω02/(2π)=2 896.0 MHz代入式(8)，参考图4中的拟合结果，取ω1/(2π)=5.2 MHz，τ=276 ns，t=90 ns，115 ns和140 ns，t0为时间零点矫正，得到ω01附近荧光强度随f的变化，如图6(b)所示.从模拟结果可见，不同的t会影响荧光强度的数值，但不会改变峰的位置.峰的位置只与ω01有关.时间零点矫正项t0的作用与t是类似的.

(a)实验结果

从图(6)中可以看出，连续波实验中，固定微波作用时长t是可行的，因为t不会影响共振峰的位置. 由于t的取值会改变荧光的相对大小，因而荧光测量精度的限制更可能是导致共振峰测量误差的主要原因.

3.5 静磁场对连续波实验的影响

在本实验中，静磁场导致了|ms=±1〉能级的去简并，即塞曼效应. 改变磁场会使荧光强度-微波频率图中的共振峰间距发生改变，然而在实验装置中，静磁场是由1块可以在底座上左右平移的小磁铁提供(见图2). 磁铁的移动会导致金刚石处的磁场大小和方向同时改变.

左右移动磁铁，共振峰的位置发生了对称移动，如图7所示. 更特别的是，当小磁铁距离金刚石较远(-6 cm和-5.25 cm)时，荧光曲线只有1组对称峰；当磁铁靠近金刚石时，在位置-4 cm处出现2组对称峰，在位置-3 cm处，产生最多4组对称峰. 该现象容易给学生造成困扰.

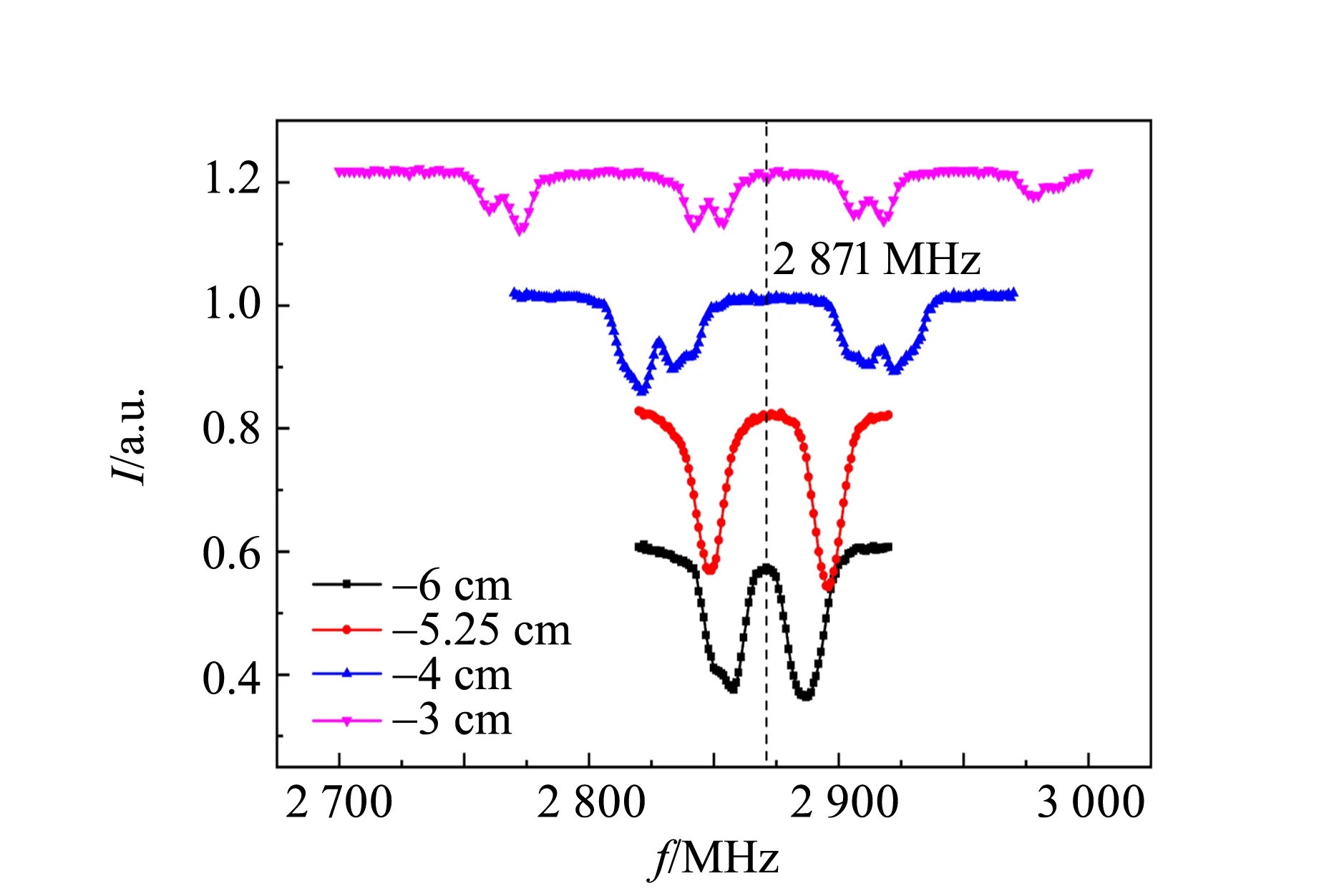
图7 小磁铁位置的影响

事实上，上述分析均只考虑单个(或者单一取向)NV色心. 由于单个NV色心的荧光信号非常弱，也较难制备，因此实验中所用的金刚石为多个NV色心的系综. NV色心有4个可能的取向，外磁场在这4个方向上的投影大小不同，导致能级产生不同程度的劈裂[16].

通过该实验现象的定性解释，学生能够理解在实验前应如何调节磁场参量：使磁场在某个NV色心取向上的投影最强，表现为连续波实验中只观察到2个共振峰. 这样，可以近似认为实验符合单一取向的NV色心模型，降低对之后量子计算的影响. 科研中一般使用单自旋的NV色心[5]，可以避免此问题. 同时，基于外磁场和4个不同取向的NV色心间的相互作用，NV色心系综还可以用于磁场的精密测量[17].

4 结束语

介绍了基于金刚石NV色心体系进行量子计算的基础内容，即量子比特的初始化、调控及读出. 为更好地帮助学生理解，设计并拓展了拉比振荡相关教学内容：通过拉比振荡实验，了解微波与自旋的相互作用，熟悉量子态的初始化及读出方法；讨论拉比振荡实验中微波频率的影响，从而引出测量共振频率的方法；通过连续波实验测量共振频率，并讨论测量过程中微波时长参量对测量结果的影响；改变磁铁位置，定性展示了NV色心的系综特性，让学生了解实际仪器中如何进行参量优化. 通过该教学设计，对学生进行启发式教学，引导学生主动思考，帮助学生对量子调控的原理和技术理解得更加全面，为进一步实现量子计算打下良好的基础.