基于Vine Copula的投资组合风险度量和相关结构研究

闫海波，李明明

摘 要：本文选取了沪深300下六个行业指数，分别用C-Vine、D-Vine、R-Vine进行相关结构建模。研究发现：D-Vine结构对相关结构的拟合程度最好，在不断引入新行业指数后，可以明显地发现降低其结构的相关性。然后对其投资组合进行风险性度量，VaR经常作为衡量风险的指标，但VaR不符合资产的一致性风险测度和无法捕捉尾部极端风险，故使用CVaR作为投资组合风险的指标。综上，资产之间的相依结构能起到优化投资组合的效果，在降低投资组合风险的同时增加了回报率。

关键词：Vine Copula;GARCH-EVT;CVaR;投资组合

中图分类号：F830.59  文献标识码：A  文章编号：1673-260X（2022）05-0040-05

引言

投资组合问题一直是投资者所关注的问题，随着金融一体化的进行，市场间的波动相依性逐渐加强。尤其是在全球疫情期间，全球经济低迷，给投资者带来了巨大的损失。因此研究投资组合风险和相关结构具有重大的意义。

自从Sklar在1959年引入Copula的概念以来，Copula在金融领域的应用逐渐趋于成熟。鉴于股票市场间的波动相依是非线性和条件相关的事实，学者引入了Vine Copula的图形化思想来构建资产间的条件相依结构。马薇、马会元、邓梦馨[1]对亚洲国家进行条件相依性结构稳健性分析。林宇、梁州、林子枭、吴庆贺[2]用R-Vine Copula对全球代表性的七只股票进行相依性结构分析。结果表明：在资产的风险和结构性不一的情况下，投资组合可以有效地降低风险，同时也可获取可观的收益。吴玉宝、汪金菊[3]用ARFIMA-GARCH-Copula模型对沪深股市的相关结构与投资组合风险度量进行分析。邢可可[4]使用Vine-Copula模型对原油、黄金等六种资产进行相关结构研究和投资组合风险度量。罗华健[5]运用马尔可夫Copula模型对不同经济时期的量价关系进行研究。叶五一、郭人榛、缪柏其[6，7]基于R藤Copula分析金砖四国的主要股指与全球指数之间的相依性结构，继而对各个国家的稳定性和风险传染进行研究。张帮正、魏宇、余江、李云红[8]基于EVT，分别C-Vine、D-Vine、R-Vine综合探讨中国不同金融市场之间的净相关关系。梁州、李昊、林宇[9]用Vine-Copula对全球的七大股指期货进行相依结构研究，更加准确的测量其投资组合的风险。佘笑荷、王晓芳、杨来科[10]基于藤式Copula对股票、黄金、能源类资产以及美元等六种资产进行资产间的相依性和组合波动风险研究。Han X， Liu Z， Wang S[11]使用R-vine copula方法研究了伦敦金属交易所有色金属商品期货之间的依赖结构，重点比较了结构断裂前后的依赖结构。杨坤、于文华、马静[12]运用Vine Copula和滚动时间窗的蒙特卡罗模拟方法刻画资产间的相依性和动态风险测度。

通过上述学者对Vine Copula研究的梳理，从中可以发现一些不足部分。许多学者注重对Vine Copula建模的研究，而忽略了对边缘分布拟合的精确性和尾部风险的捕捉。因为金融时间序列经常出现尖峰厚尾的特征，可能还会出现长期记忆性，故本文使用EVT的广义帕累托分布来对标准残差进行拟合。VaR经常作为衡量风险的指标，但VaR不符合资产的一致性风险测度和无法捕捉尾部极端风险，故本文使用CVaR作为投资组合风险的指标。使得本文研究更加具有现实意义。

1 理论部分

1.1 Sklar定理

设H（x1，x2，…，xn）为n维随机变量x1，x2，x3，…，xn的联合分布函数，其对应的边际分布别为F1（x1），  F（x2），…，F（xn），则存在一个函数C（·）满足：

H（x1，x2，…，xn）=C（F1（x1），F（x2），…，F（xn））

若F1（x1），F（x2），…，F（xn）是连续的，则C是唯一的。否则C仅在Rank（F1）×Rank（F2）…×Rank（Fn）上唯一。

1.2 Vine Copula模型

参数估计Vine Copula模型常用于资产投资组合的相关结构研究。Vine Copula模型是由节点和边组成的一系列树的组合，n维的Vine Copula结构含有n-1棵树和n-1个节点，设n维的Vine Copula的邊集合为Ei，节点集合为Ni，任意边为e= j（e），k（e）/D（e）∈Ei。其中D（e）表示两个节点之间的连接条件。k（e）和j（e）分别代表边e和树T（i）的两个节点。cj（e），k（e）/D（e）可以表示边e的pair-Copula的密度函数，Y={Xi}，i=1，2，…，n，YD（e）表示D（E）的条件向量。Fi和fi分别为Xi的边际分布和边缘密度函数，则Y的联合密度函数可以表示为[1]：

f（y，y，…，y）=■fk（yk）■■cj（e），k（e）/D（e）（F（yj（e）/yD（e）），F（yk（e）/yD（e）））

其中yj（e）/yD（e）和yk（e）/yD（e）为条件分布函数。

1.3 参数估计

本文选用ARMA-GARCH-EVT模型对边缘分布进行模拟，因为金融数据一般会出现尖峰厚尾的特征，故使用EVT中的广义帕累托分布对其经验分布函数进行拟合。估计Vine Copula参数使用全局似然估计方法，其函数表达式如下所示：

■■■ln（c■）（F■

（x■，t），F■（x■，t））

算法步骤如下：

（1）计算资产间的Kendall相关系数，采用最大生成树的方法确定第一棵树结构。

（2）先对其进行独立性检验，进而采用独立的Copula函数拟合数据，然后应用AIC准则为第一棵树的边确立Copula函数的类型。

（3）通过第一棵树的Copula函数运用确定条件观测值，从而又可以采用最大生成树算法来确定第二颗树的结构[7]。

（4）不断迭代下去直到所有结构及参数确定[7]。

（5）用全局似然估计方法计算模型的最终参数值。

2 实证部分

数据来源：该数据来自wind数据库中沪深300指数中金融指数、医疗指数，材料指数，能源指数，工业指数，房地产指数六个指数。选取2011年11月16日到2021年11月15日，共5092组数据。

2.1 ARMA-GARCH-EVT的建模

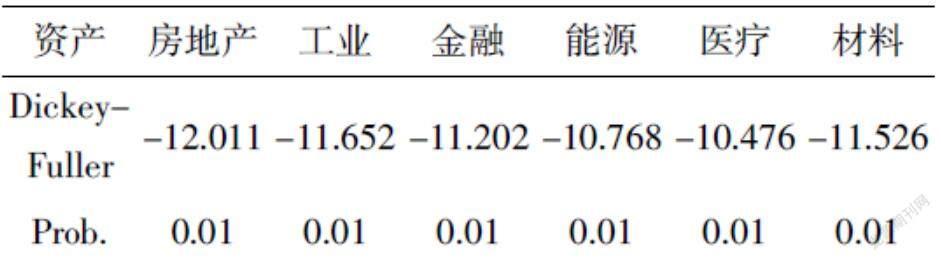
选取2011年11月16日到2019年11月15日的日收盘价数据，先对其日收盘价进行对数收益率计算，然后对其进行单位根检验，其ADF检验的结果如下：

从上表可以看出，该六组资产都通过了单位根检验，说明该序列为平稳序列。

对数收益率进行GARCH模型建模的前提就是要保证该数据具有ARCH效应。经检验，该六组数据都具有ARCH效应，在此对这六组数据进行ARMA-GARCH模型的建模，根据AIC，BIC等指标，选取最佳的ARMA-GARCH模型。基于篇幅的原因，我将最后的建模结果列于下表：

对其对数收益率进行ARMA-GARCH模型建模后，提取其标准残差进行边概率积分变化，因其分布常常呈现尖峰厚尾的特征，故使用极值理论中的广义帕累托分布对其经验分布函数进行拟合，为下一步vine-copula的建模奠定基础。

2.2 C-Vine Copula模型的建模

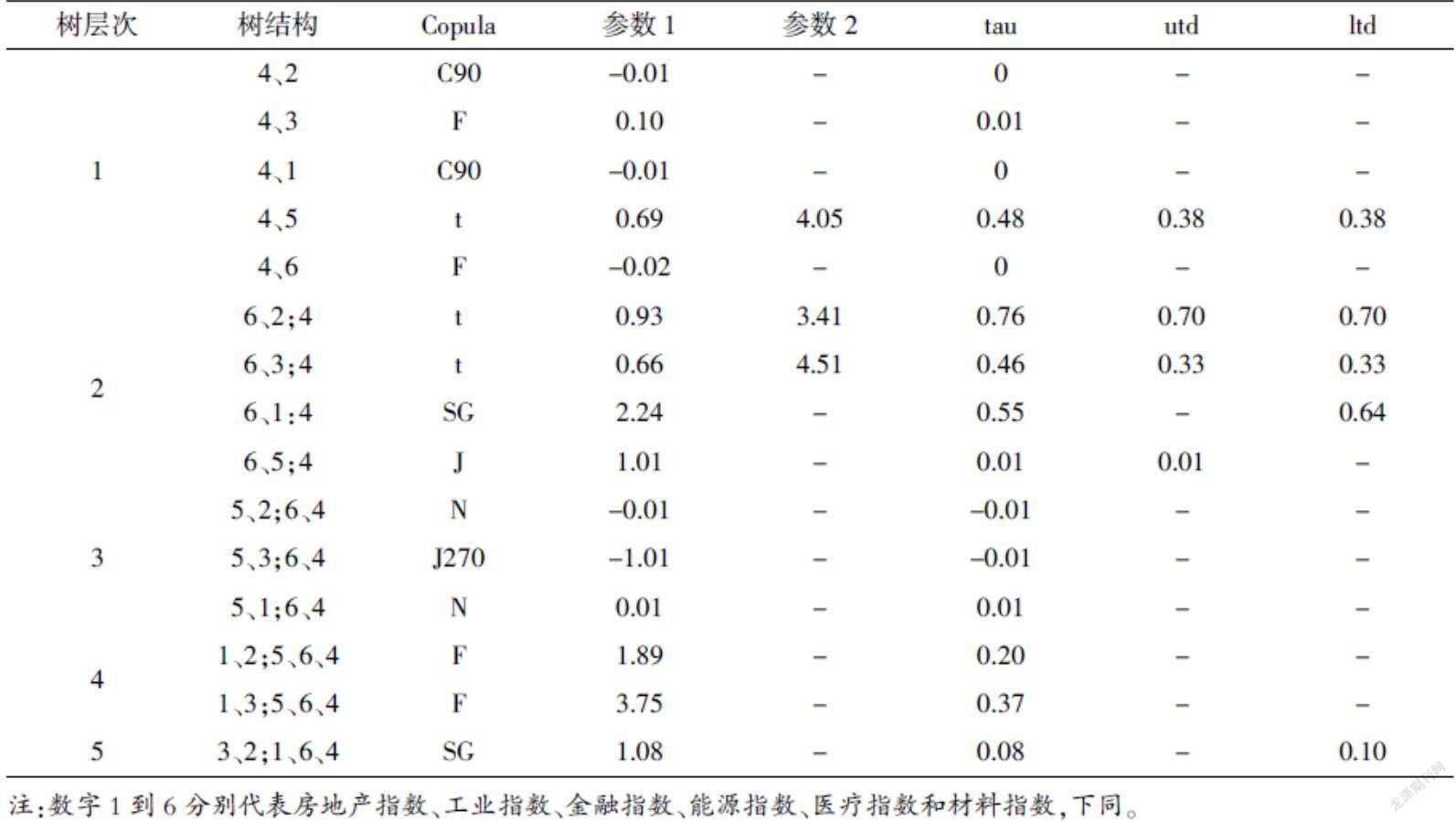
用R语言来构造C-Vine Copula模型，其结果如下表所示：

在C-Vine Copula模型第一层树中，能源指数（4）处于树的结点的位置，说明能源指数（4）与其它指数之间的相关性是最大的。可以发现工业指数（2）和能源指数（4），房地产（1）的Kendall相关系数均为-0.01，上下尾部对称，故它们的连接Clayton copula函数旋转90度来描述。从第一层树中可以发现能源指数（4）和医疗指数（5）具有很强的正相关性，当股市处于熊市时，能源指数（4）和医疗指数（5）很大可能性会出现同时下跌，会大大地增加投资的风险。其上下尾部相关系数相同，故可以用t copula函数来进行连接。能源指数（4）和材料指数（6）的Kendall相关系数为负值，则表明能源指数（4）和材料指数（6）进行投资组合降低了整体的风险，使用Frank Copula函数来描述它们的相关结构。

在第二层结构中，引入能源指数（4）的情况下，工业指数（2）、金融指数（3）与材料指数（6）之间的相关结构均用t Copula函数来衔接。可以发现引入能源指数（3）后，整体的风险降低了，尤其医疗指数（5）和材料指数（6）之间更加明显。从第三层树到第四层树中可以发现，随着新的行业指数的进入，整体的风险逐渐降低。但在第五层树中，随着房地产指数（1）和医疗指数（5）的加入，整体风险增加了。这是在于房地产指数（1）和医疗指数（5）与其它指数之间的相关系数为正值，它们的加入，非但没有降低风险，反而增加了风险。因此在进行投资过程中，尽量避开相关性较强的资产进行组合，这样才能有效地规避风险。

2.3 D-Vine Copula模型的建模

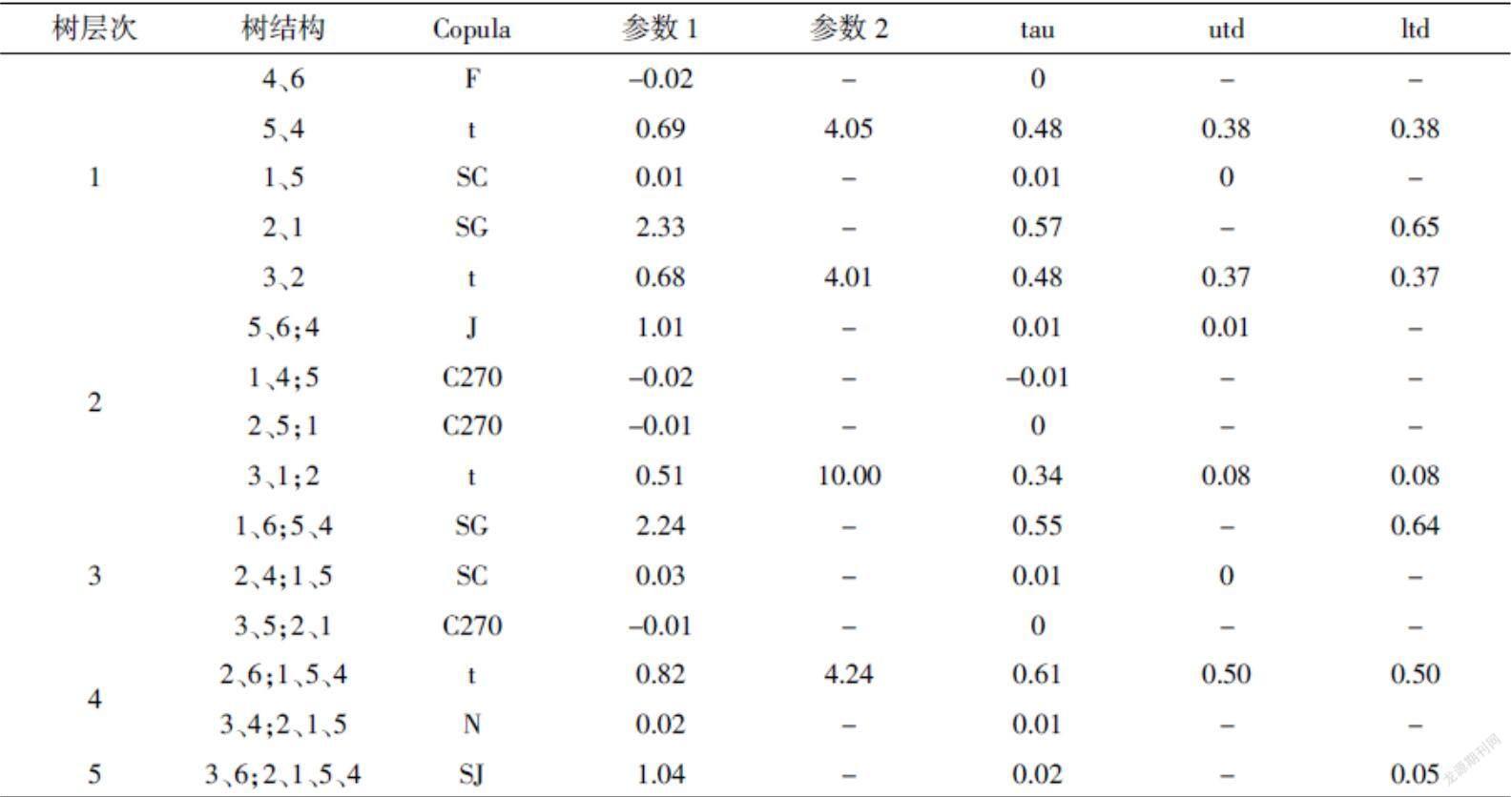
用R语言来构造D-Vine Copula模型，其结果如下表所示：

在D-Vine Copula模型第一層树中，它没有中心节点，金融指数（3）和材料指数（6）处于树的边缘部分，表明金融指数（3）和材料指数（6）与其他四个指数关联程度不大。据模型可以看出：工业指数（2）和金融指数（3）、能源指数（4）和医疗指数（5）均用t Copula函数进行相关结构研究。在第二层树中，在引入能源指数（4）的情况下，医疗指数（5）、材料指数（6）和能源指数（4）的投资组合有效地降低整体风险。在引入房地产指数（1）和医疗指数（5）的情况下，房地产指数（1）和能源指数（4）及工业指数（2）和医疗指数（5）均用Clayton copula函数旋转270度来描述其相关结构。在第二层树到第五层树从中可以发现，引入一个新的市场指数之后，都有效地降低了其投资组合的风险。

2.4 R-Vine Copula模型的建模

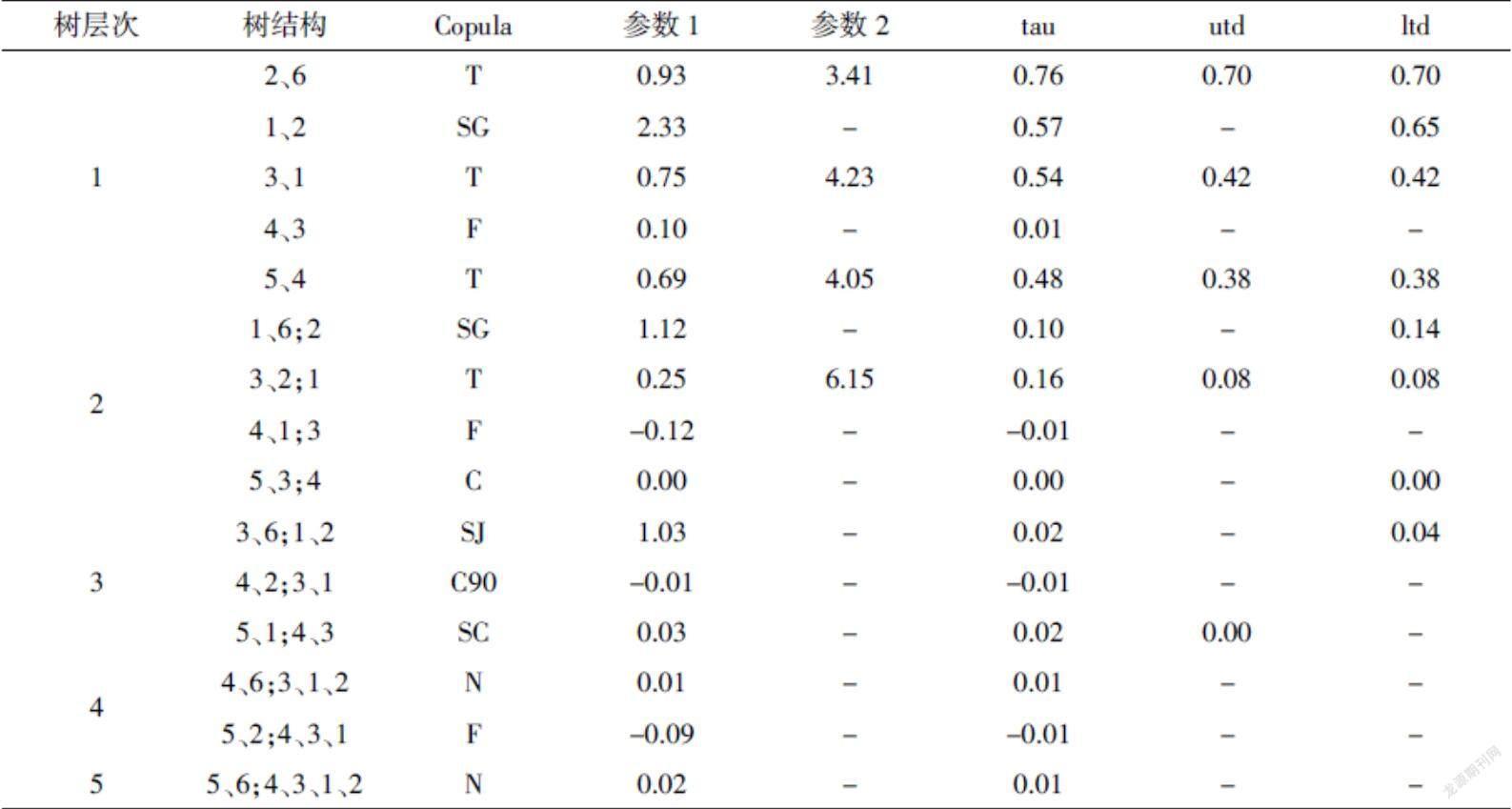
用R语言来构造R-Vine Copula模型，其结果如下表所示：

在R-Vine Copula模型第一层树中，它与D-Vine模型一样没有中心节点。医疗指数（5）和材料指数（6）处于树的边缘部分，表明医疗指数（5）和材料指数（6）与其他四个指数关联程度不大。从中可以看出每两个行业指数之间的Kendall系数都为正值，其意味着当熊市来临时，任何两个资产进行投资组合在很大可能面临同时下跌的危险。从中可以看出工业指数（2）和材料指数（6）、金融指数（3）和房地产指数（1）、能源指数（4）和医疗指数（5）之间均用t Copula函数来描述其相关结构。在第二层带第五层，可以明显地看到，随着资产数量的不断增加，资产间的Kendall系数逐渐变小，其风险的逐渐变小。

2.5 Vine Copula模型的拟合效果比较

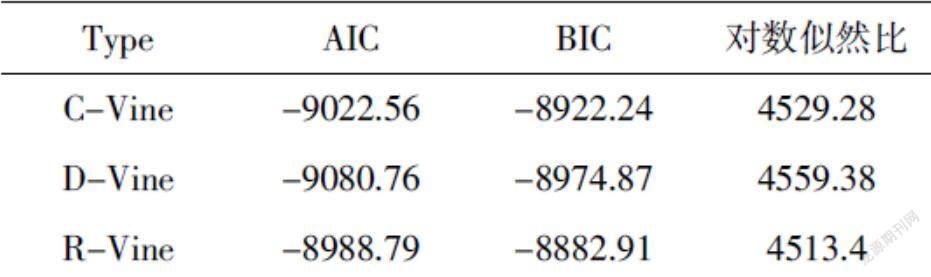
本文使用极大似然估计对Vine Copula模型进行拟合效果比较，结果如下表所示：

从上表可以看出：根据AIC、BIC、对数似然比可以看出，D-Vine模型的拟合程度最好，能相对准确的描述资产组合的相关结构。

2.6 CVaR的度量

VaR经常作为衡量风险的指标，但VaR不符合资产的一致性风险测度和无法捕捉到尾部极端风险，故使用CVaR作为投资组合风险的指标。

从上表可以看出，金融指数属于低风险产品，而其它五个指数都属于中高风险产品，当对其进行投资组合时，其明显降低了投资风险。对于不同的置信水平，假如投资者是一个风险偏好者，可以选择比较高的置信水平，同时也会面临比较大的损失。

2.7 Kupeic检验

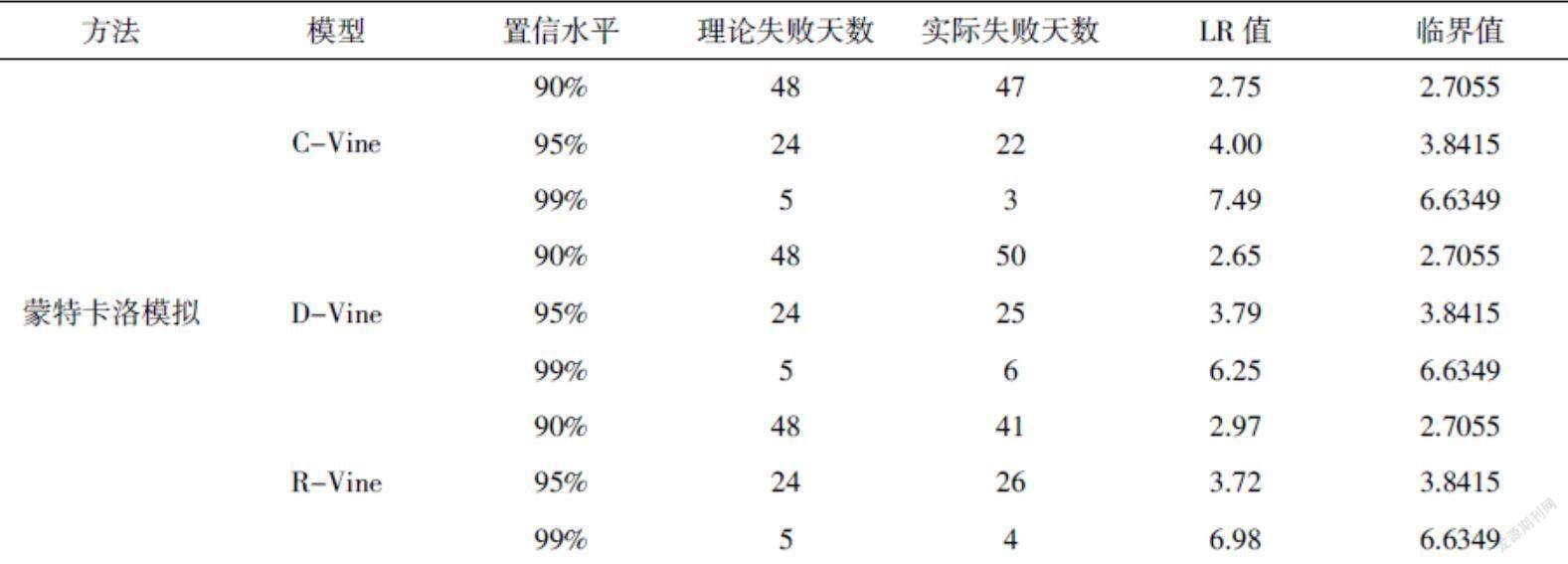
将使用2019年10月25日到2021年11月15日的数据，共500组数据，对CVaR进行回溯检验，使用Kupeic检验。

从上表可以看出D-Vine模型的拟合效果最好，更能对投资组合风险进行相对准确的刻画。

3 结论及建议

（1）合理配置资产比例。从Vine Copula结构可以看出，每个资产之间的Kendall系数不一样的，材料指数的风险较高，可以适量减少其资产投资比例。金融资产的风险较低，可以适当的增加其资产投资比例。这样可以有效地规避其投资风险。

（2）合理选择和分散投资风险。从Vine Copula模型的结果可以看出，引入一个新的行业指数之后，整体的风险逐渐降低。但各个资产之间的相关性不同，在进行投资组合时，尽量避免将相关性强的资产进行投资组合。例如工业指数和材料指数之间的相关性很强，在熊市时，会出现同时下跌的可能性，这样不能分散其投资风险。因此在进行投资时，要选择相关性较弱或者相关性为负的产品种类，这样可以有效地规避风险。

（3）重视小概率事件风险。CVaR对不同投资组合的反应更为敏感，也就是在小概率下的风险值。忽视小概率事件会导致严重后果，如恒大公司的濒临破产等“黑天鹅”事件。因此注重小概率事件是很有必要的。

参考文献：

〔1〕马薇，马会元，邓梦馨.基于R Vine Copula模型的条件相依结构稳健性研究[J].统计与决策，2021， 37（20）：30-34.

〔2〕林宇，梁州，林子枭，吴庆贺.基于高维R-vine Copula的金融市场投资组合优化研究[J].系统工程理论与实践，2019，39（12）：3061-3072.

〔3〕吴玉宝，汪金菊.沪深股市的相关结构分析与投资组合风险度量——基于ARFIMA-GARCH -Copula模型[J].运筹与管理，2016，25（02）：220-225.

〔4〕邢可可.基于Vine Copula的投资组合相关结构和风险测度研究[D].安徽财经大学，2021.

〔5〕罗华健.基于Copula金融市场间的相关性及风险预测[D].山东科技大学，2020.

〔6〕郭人榛.基于R藤Copula变点模型的金融传染性与稳定性检验[D].中国科学技术大学，2018.

〔7〕叶五一，郭人榛，缪柏其.基于R藤copula变点模型的金砖四国金融传染性与稳定性检验[J].中国科学技术大学学报，2018，48（08）：655-666.

〔8〕张帮正，魏宇，余江，李云红.基于EVT-Vine-copula的多市场相关性及投资组合选择研究[J].管理科学，2014，27（03）：133-144.

〔9〕梁州，李昊，林宇.R-Vine Copula、极值理论与股票市场组合风险测度[J].南方金融，2018，34（07）：28-38.

〔10〕佘笑荷，王晓芳，杨来科.基于极值理论与藤式Copula模型的多市场投资组合选择[J].统计与决策，2017，37（20）：49-51.

〔11〕Han X， Liu Z， Wang S. A R-Vine Copula Analysis of Non-ferrous Metal Futures with Application in Forecasting Value-at-Risk[J]. SSRN Electronic Journal， 2020.

〔12〕楊坤，于文华，马静.基于vine copula的股市风格资产组合风险预警研究[J].武汉金融，2019，25（11）：51-59.