负载口独立控制系统主被动加载试验台振动特性分析

陶 扬， 刘凯磊,2,3， 康绍鹏， 强红宾， 王友定， 郭 言

(1.江苏理工学院 机械工程学院， 江苏 常州 213001；2.江苏大学 国家水泵及系统工程技术研究中心， 江苏 镇江 212013；3.国机重工集团 常林有限公司，江苏 常州 213136；4.江苏恒立液压科技有限公司， 江苏 常州 213000)

引言

近年来，随着世界能源危机的爆发，节能、高效、低碳、环保已经成为当今世界的主题，在液压技术领域内，如何降低能耗一直是备受关注的话题[1-2]。

在传统阀控液压系统中，由于采用了1根阀芯，液压阀在进口节流的时，出口同时进行节流，造成了重复的节流损失[3]。为了解决该问题，1987年BACKÉ教授首次提出了利用4个插装阀控制液压执行器的负载口独立控制系统，通过不同的逻辑控制完成了液压执行器的正反向运动控制[4]，随后，VALENTINO C等[5]、KYUJEONG C等[6]、丁孺琦等[7]、王涛等[8]分别对负载口独立控制系统中液压泵的转速、流量再生、耦合特性、阀芯位移控制等不同方面进行了研究，并取得了一定的进展。

与传统阀控液压系统类似，在负载口独立控制系统中，同样存在着主动型负载工况和被动型负载工况，液压执行器在两种工况下的运动控制亦称为主动控制和被动控制。因此，在对负载口独立控制系统进行运动控制性能试验测试时，需要分别对主动控制和被动控制进行性能测试。

根据负载口独立控制系统主被动控制加载试验测试要求，本研究采用了双缸对顶或双缸互拉的方式，完成了试验台的设计，从而可以实现主动加载、被动加载和主被动交替加载试验。然而，在实际加载过程中，主被动加载力的大小、方向、振动频率等会对试验台的振动特性产生一定影响，从而影响试验效果。

为了分析不同因素对多种试验台振动特性的影响，王成军等[9]抽取六自由度变胞试验台中变形最大的蛇形板簧和加速度载荷最大的动平台进行前四阶振动模态和谐响应的分析，验证了结构薄弱部件蛇形板簧和动平台的振动频率满足工作需求；寸文渊等[10]通过ANSYS建立飞机液压管路有限元模型并通过模态分析法对管路进行了改进，避免了危险固有频率的产生；周杰等[11]通过赫兹弹性体接触理论优化丝杠可靠性试验台有限元模型，并与原模型的固有频率进行对比优化；邓敏泰等[12]对新能源汽车高速变速试验台进行振动测试，验证了谐响应分析中转子最大转速是安全可靠的；马晓等[13]利用横向和纵向的模态分析使海水泵转子系统的一阶转速远离固有频率；魏冰阳等[14]将闭功率流锥试验台的SolidWorks模型导入ANSYS中进行了静力学和模态分析，并验证齿轮箱满足设计要求；TSUKAMOTO Y等[15]检查了刚性圆形地基试验台位于饱和砂层结构中的沉降工作，通过地震响应时间、激励信号强度等方面对试验台的振动频率进行了测试；CHRISTOPHE N等[16]搭建了预加载试验台振动系统，研究了不同静态预加载力下固有频率变化的大小，并指出了振幅衰减现象。

本研究以负载口独立控制系统主被动加载试验台为研究对象，建立试验台力学模型，分别通过静力学分析、模态分析、位移响应分析、加速度响应分析等，研究试验台的静态变形量、固有频率的振动形态、结构薄弱下的振动频率、横向加速度传递路径，从而为加载试验性能测试提供有效依据。

1 加载试验台结构组成与工作原理

负载口独立控制系统主被动加载试验台主要包括工作液压缸、加载液压缸、油缸底座机架、脚座、拉杆、联轴器、位移传感器等，试验台的结构如图1所示。工作液压缸和加载液压缸的材料均为结构钢，两液压缸的基本参数相同，如表1所示。

表1 液压缸基本参数Tab.1 Basic parameters of hydraulic cylinder

试验台分为左右两部分，左侧为工作部分，右侧为加载部分。左侧工作液压缸通过管路与负载口独立控制阀相连，并且通过位移传感器检测工作液压缸活塞杆的运动状态，从而通过对负载口独立控制阀的控制实现工作液压缸的伸出或缩回运动控制；右侧加载部分中，加载液压缸的活塞杆通过联轴器与工作液压缸的活塞杆相连，通过对加载液压缸实施恒定推力或拉力的加载运动控制，可以实现对工作液压缸的主被动加载。试验台主体部分包括机架、拉杆、脚座等，为试验台提供稳定的支撑。

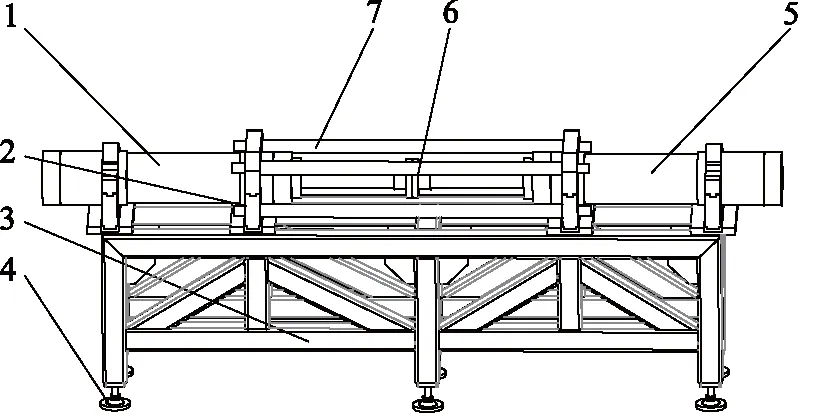
1.工作液压缸 2.位移传感器 3.机架 4.脚座5.加载液压缸 6.联轴器 7.拉杆图1 负载口独立控制系统主被动加载试验台结构图Fig.1 Structure of active and passive loading test bench for independent metering control system

从试验台的结构可以看出，在加载液压缸加载过程中，其加载力不仅影响试验台整机的静力学特性，而且随着加载力的大小、方向、频率等不断变化，会引起整机振动，因此，本研究对试验台进行静力学分析与振动分析。

2 有限元分析前处理

2.1 网格划分

为了方便展开仿真分析，对液压缸和底座的试验台模型进行了简化，去除了液压控制元件和传感器。考虑到液压试验台的体积较大，所需绘制的网格单元较多，采用有限元网格划分软件Hypermesh对其进行网格划分，设置单位网格为5 mm，如图2所示，共得到1043959个节点、725350个网格单元。

2.2 定义材料属性

试验台的材料大多为钢材，因此为了简化模型，将结构钢设置为模型材料，查阅相关资料，结构钢的参数性能如表2所示。

3 试验台静力学分析与模态分析

3.1 静力学分析

在加载液压缸对工作液压缸施加加载力的过程中，两缸腔内均会产生压力，加载力稳定性控制试验要求将液压系统压力控制在20～30 MPa区间内的一个值，因此以最大压力30 MPa进行分析，将有限元网格模型导入进Workbench并建立静力学分析模块， 分别对两缸施加30 MPa的压力， 其中，主动型负载工况下的压力方向为无杆腔到液压缸缸头，将其简称为正向压力；被动型负载工况下的压力方向则施加在活塞套、活塞杆上，简称为反向压力。得出正向和反向压力的位移、应力云图，如图3～图6所示，正向压力和反向压力所产生的最大位移为别为0.37 mm和0.22 mm，最大应力分别为109 MPa和94 MPa，正向压力产生的位移和应力较大，产生的振动分析也会越明显，因而越容易对试验台物理结构产生危害性影响。因此，对正向压力的分析比反向压力重要，且只要保证正向压力的加载频率对试验台物理结构无损害，即可保证反正压力同样无损害，因此选择正向压力作为研究对象更为合理。正向压力产生的总体位移在试验台的正中间，即拉杆、联轴器以及底部支架的中间，最小变形量在脚座和支架两侧， 其最大变形量满足设计要求。最大应力和应变均在拉杆和压板的连接处，最小应力集中在底部支架结构，大部分应力值远小于结构钢屈服强度，且最大等效应力的109 MPa远小于结构钢屈服强度的235 MPa，满足设计要求。通过静力学分析可知，试验台的网格模型较为准确，静力学模型搭建合理，在实际工况中将加载力控制在30 MPa以内，试验台处于安全工作范围内。因此，可以将静力学分析中的正向腔内压力作为后续谐响应分析中的激励信号。

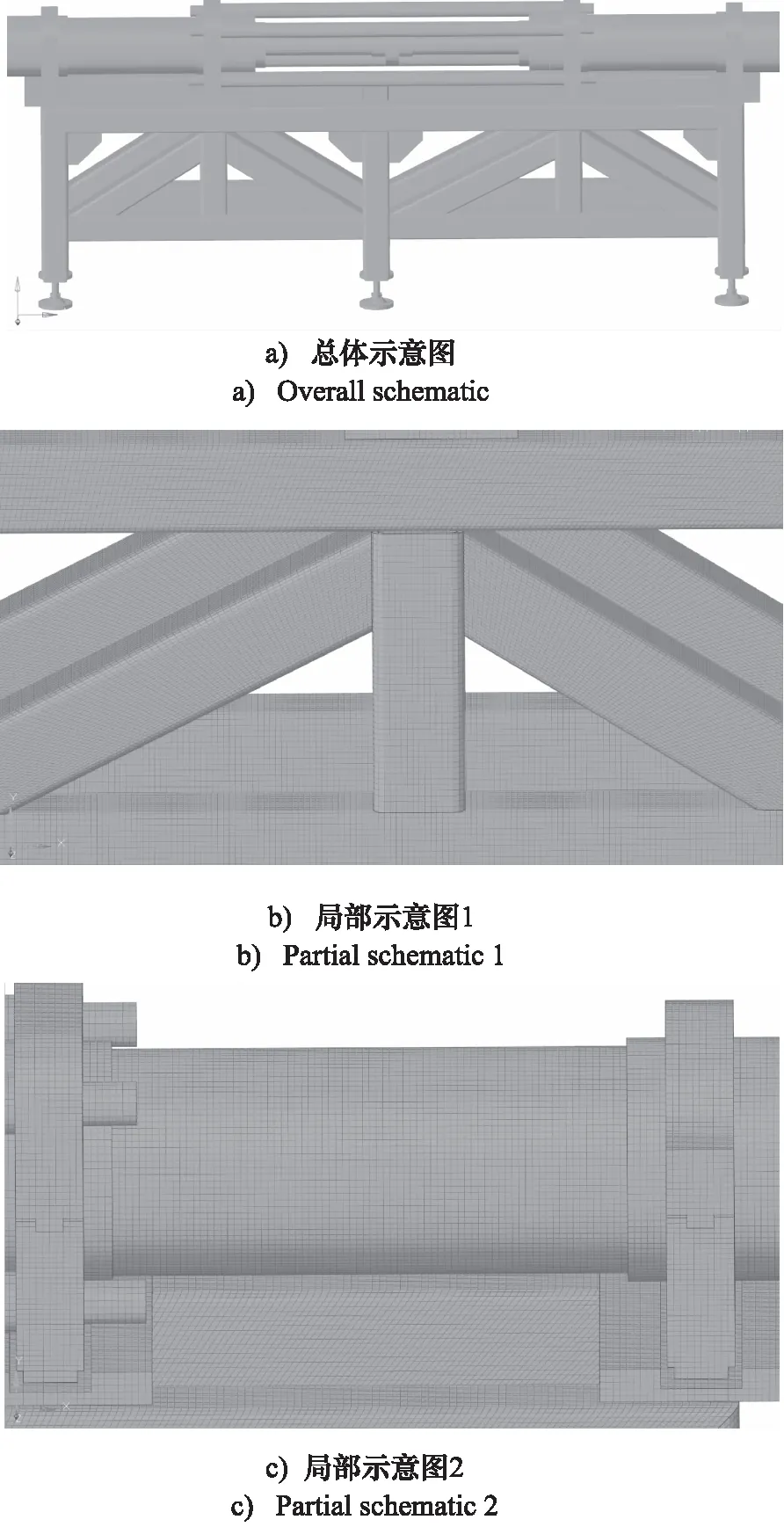
图2 Hypermesh下绘制的试验台网格图Fig.2 Test bench meshed by Hypermesh

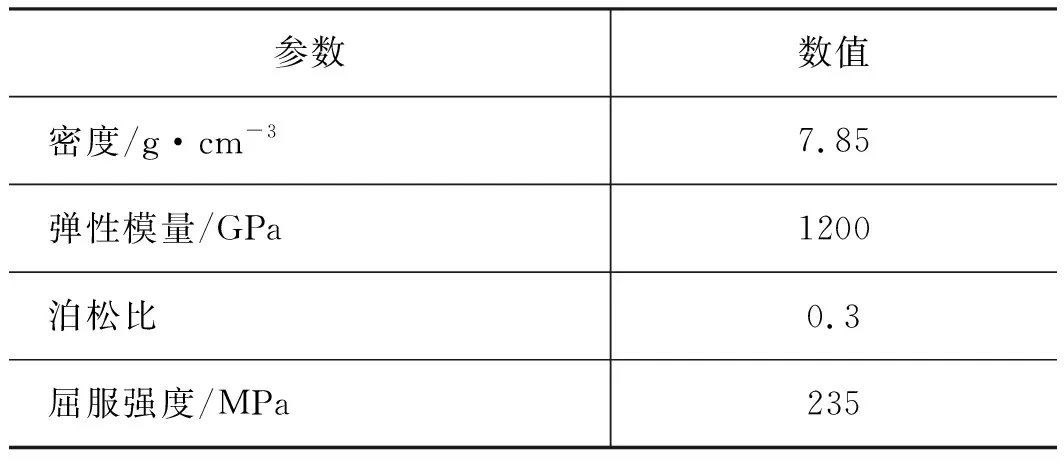
表2 结构钢基本参数Tab.2 Basic parameters of structural steel

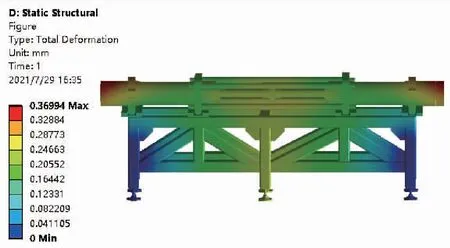
图3 正向压力的位移云图Fig.3 Displacement of positive pressure

图4 正向压力的应力云图Fig.4 Stress of positive pressure

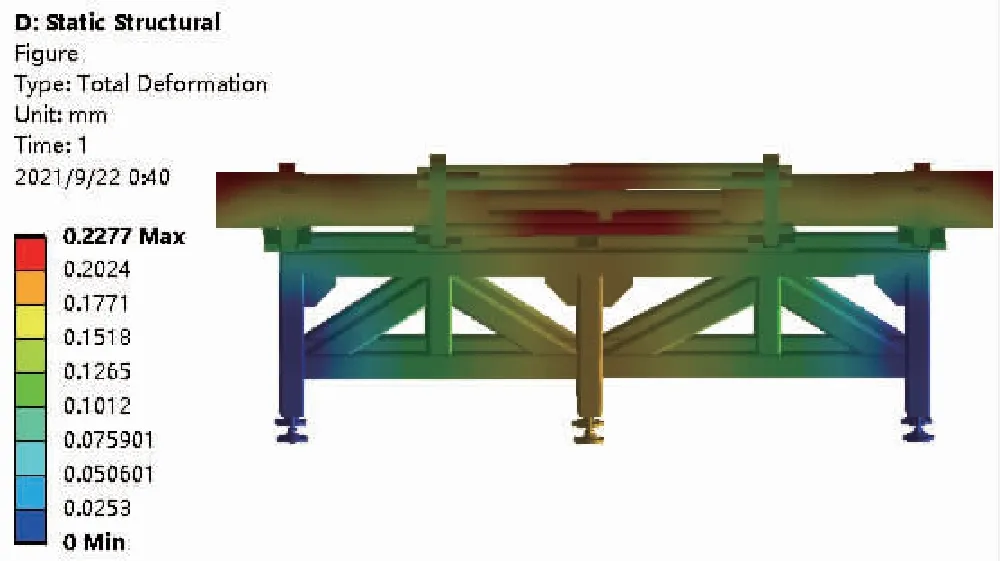
图5 反向压力的位移云图Fig.5 Displacement of reverse pressure

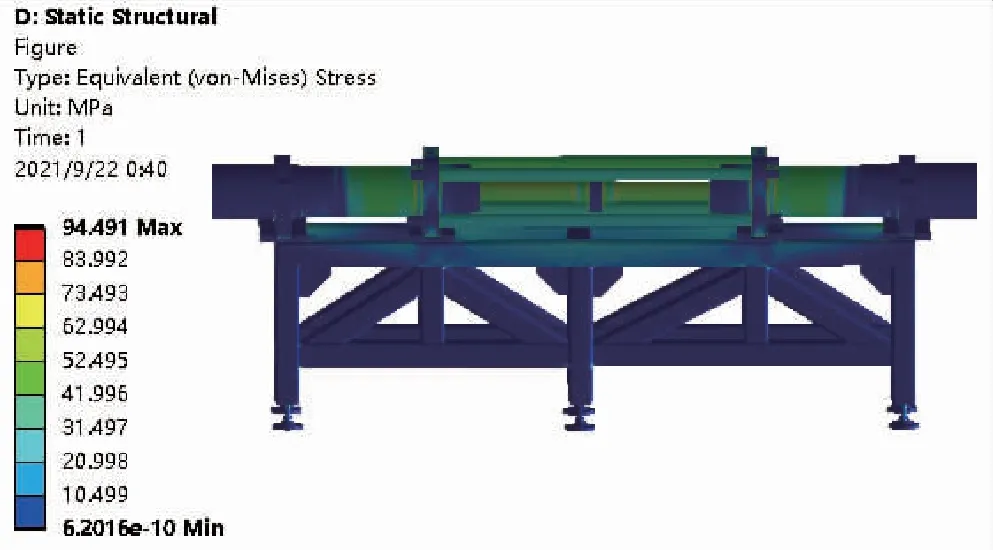
图6 反向压力的应力云图Fig.6 Stress of reverse pressure

3.2 振动模态分析

由经典力学理论可知，物体运动的通用动力学方程如下：

Mx″+Cx′+Kx=F(t)

(1)

式中，M—— 质量矩阵

C—— 阻尼矩阵

K—— 刚度矩阵

x—— 位移矢量

x′ —— 速度矢量

x″ —— 加速度矢量

F(t) —— 力矢量

由于振动模态分析是试验台的自由振动，不考虑任何外力影响，且自由振动状态下阻尼矩阵对力学特性的影响较小，可以忽略不记，因此，该动力学方程可以简化为如下：

Mx″+Kx=0

(2)

另外，试验台自由状态下的振动为简谐振动，位移为正弦函数，因此公式可以简化为：

K-(2πf)2Mx=0

(3)

式中，f—— 物体振动频率。

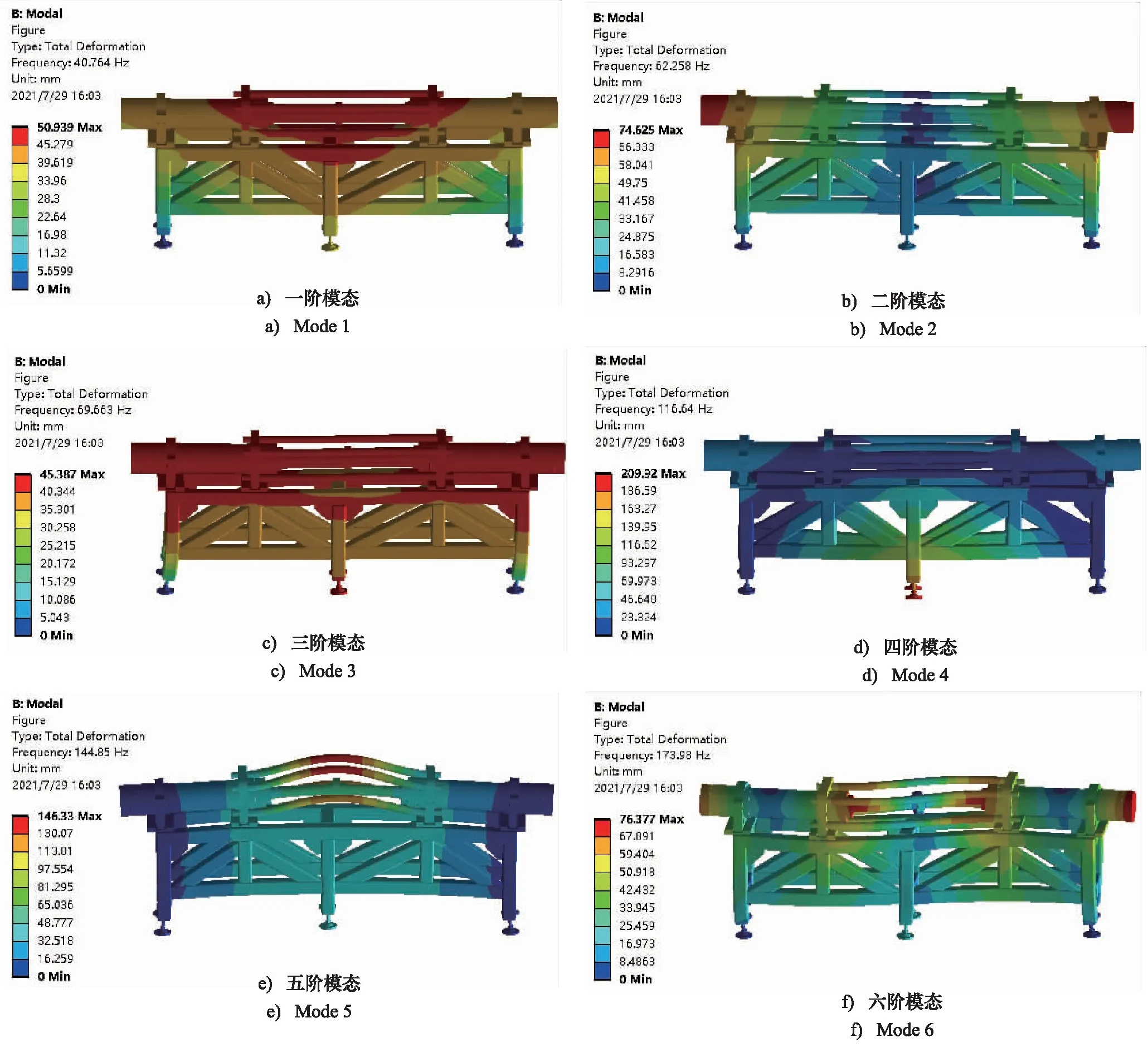
图7 试验台前六阶模态Fig.7 Mode 1 to 6 of test bench

考虑到低阶模态对物体振动特性影响最大，采用有限元分析软件ANSYS Workbench的Modal模块对试验台的前六阶模态进行仿真分析。由于加载缸的加载运动会使得试验台受两侧挤压，从而上下振动，因此将4个角的脚座处设置约束，中间两脚座不做约束，仿真得出试验台前六阶的固有频率，固有频率的大小与试验台本身的质量、刚度和尺寸有关，仿真结果如图7所示。

从图7可以看出，一阶振动的位移响应分布在整个试验台中，其中拉杆位移量最大，呈现拉杆弯曲振动；二阶振动的位移响应主要分布在两侧液压缸上，中间部分几乎没有位移响应，呈现液压缸弯曲振动；三阶振动的位移响应与一阶类似，呈现整体弯曲振动；四阶振动的位移响应主要分布在中间钢管以及斜钢管，呈现中间支架弯曲振动；五阶振动的试验台出现明显变形，拉杆向上弯曲，且液压缸底座出现横移；六阶振动的位移响应较大且液压缸的活塞杆和右侧活塞盖出现明显的扭转弯曲振动现象，如表3所示。

考虑到加载系统无法实现太高的振动频率，因此，影响试验台振动的主要模态为一、二、三、四阶模态，而在实际加载过程中，影响试验台整机振动的主要模态为一阶模态，固有频率为40.764 Hz，最大振幅为50.939 mm。另外，固有频率由小到大变化，而频率太小则又无法清晰表达出仿真结果，因此将前四阶的固有频率作为后续谐响应分析中的扫描频率范围。

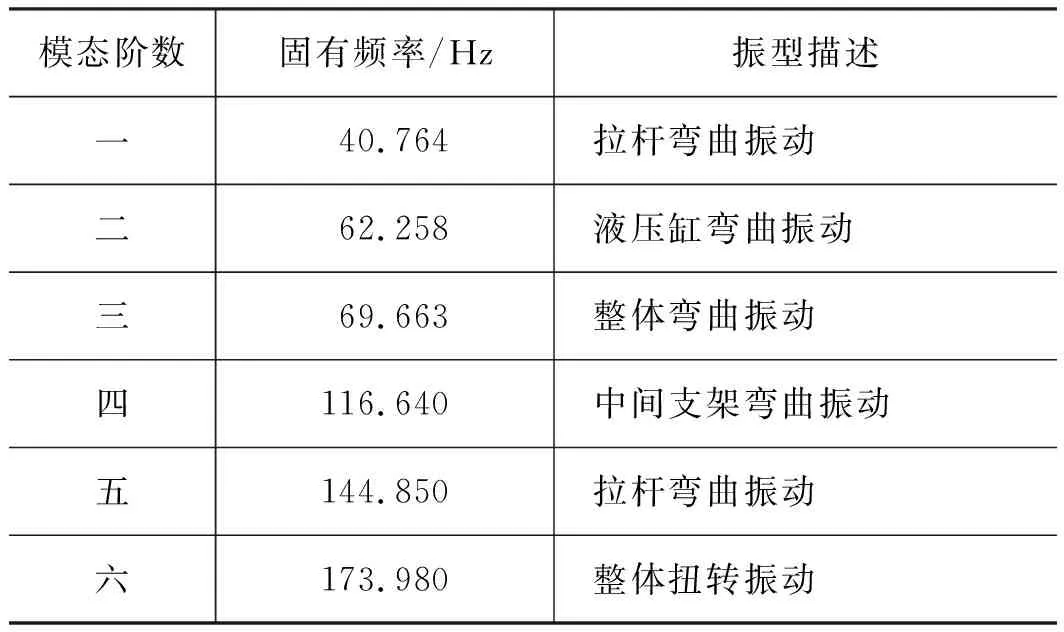
表3 前六阶固有频率及振型Tab.3 Once to sixth natural frequency and mode shape

由于试验台是对液压系统进行测试，因此，工作缸是在液压系统的驱动下作往复运动，工作缸的往复运动频率将是影响试验台振动的主要因素，如若工作缸的往复运动的振动频率达到试验台的一阶模态固有频率40.764 Hz，试验台将会产生共振，从而对试验台造成不良影响。工作缸的往复运动是在液压系统驱动下完成的，因此其往复运动的振动频率取决于液压系统的动态特性，而液压系统的动态特性又由液压系统的固有频率决定[17]，因此，当液压系统的固有频率超过试验台的一阶模态固有频率40.764 Hz时，工作缸的往复运动的振动频率必须控制在40.764 Hz以下，从而避免产生共振。

4 试验台谐响应分析

4.1 位移谐响应分析

谐响应分析又称受迫振动分析，是一种在正弦激励信号作用下的稳态振动的计算，这种正弦激励信号可以是加速度，也可以是力或者压力，再通过一段连续变化的扫频可计算出位移、速度、加速度和扫描频率的关系，本研究采用模态叠加法进行计算机仿真。根据式(1)可知物体动力学通用方程，计算固有频率时由于不受外力影响，力矢量默认为0，而在谐响应分析中力F为：

F=F0cos(2πf0t)

(4)

式中，F0—— 用作正弦激励信号的固定初始力

f0—— 扫描频率

t—— 时间

由静力学分析可知，双缸互拉、双缸对顶的加载方式所产生的正反向压力仅需要控制在30 MPa以内，因此将此加载力作为激励信号输入，由于此输入信号为x轴的轴向力，因此无需分析轴向位移，再通过模态分析得出的第四阶固有频率附近作为扫频区间，得出100 Hz下的试验台总体位移响应如图8所示。

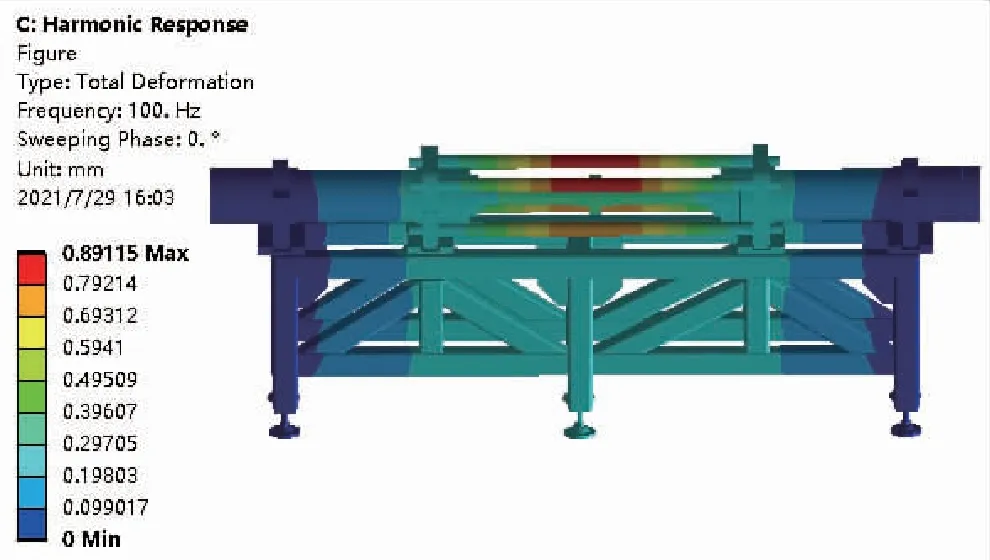
图8 总体位移响应图Fig.8 Total displacement response

根据图8可知，试验台位移响应最大处在拉杆中间，最大位移为0.89 mm，而最小处则在两侧的活塞盖与支架上。可以明显看出，最大位移只集中在整个试验台中上一小部分，大部分位移响应为0.30 mm，集中在液压缸最右侧的导套以及下方支架的正中间，位移响应越往试验台的两侧越小，且最小处在试验台最左侧和最右侧，起到固定约束处的脚座位移响应为0 mm。另外，通过上述模态分析的位移变化量选取试验台的4处节点：活塞杆、活塞盖、液压缸和支架上表面，得出横向位移x1和垂直位移x2响应变化随扫描频率的变化关系，如图9所示。

根据所得径向位移响应曲线图可知，加载系统所受激励信号所产生的振动中，垂直位移响应总体上远大于横向位移响应，可见试验台的振动幅度主要为上下振动，左右振动的幅度较小。在横向位移响应中，所有节点在扫描频率处于40 Hz附近时数值均发生明显变化，可知此区间内试验台的位移会发生突变，另外，除了支架上表面变化不明显外，其余节点在70 Hz附近时同样发生明显的位移突变，上述2个区间结构钢容易发生断裂；在垂直位移响应中，所有节点同样在70 Hz附近发生位移突变，产生断裂。通过对比模态分析所得固有频率可知，位移响应发生突变的位置区间与试验台的一阶、二阶固有频率接近，可见模态分析与谐响应分析处理结果较为正确，且试验台自身的固有频率对自身的振动影响很大，容易引起共振，因此，在试验台加载试验中，应当将加载力的振动频率控制在35 Hz以内，避免产生试验台物理结构的断裂以及共振现象。

图9 谐响应分析位移响应Fig.9 Displacement harmonic response analysis

4.2 加速度谐响应及振动传递路径分析

加速度的大小能有效地表示试验台受激励信号后的振动状态，同样采用位移响应分析中的激励信号对试验台的加速度响应进行分析，结果如图10所示。

从图10中可以看出，加速度响应的整体分布与位移响应分布一致，说明试验台在位移响应分析和加速度响应分析中，整机变形情况相同。

根据位移响应分析可知，试验台横向加速度响应受试验台固有频率的影响较大，利用谐响应分析中加速度变化响应线图对试验台横向加载力分布所产生的振动路径进行分析，为了对试验台的减振提供参考依据，分别选取试验台中若干主要、次要振动节点进行仿真分析，主要振动节点与次要的区别在于，主要振动节点由于承载的加速度载荷较大，在所分析的扫描频率范围内仍无法到达最大值，次要振动节点承载的加速度载荷较小，在小范围的振动频率内即可监测到加速度载荷的变化。

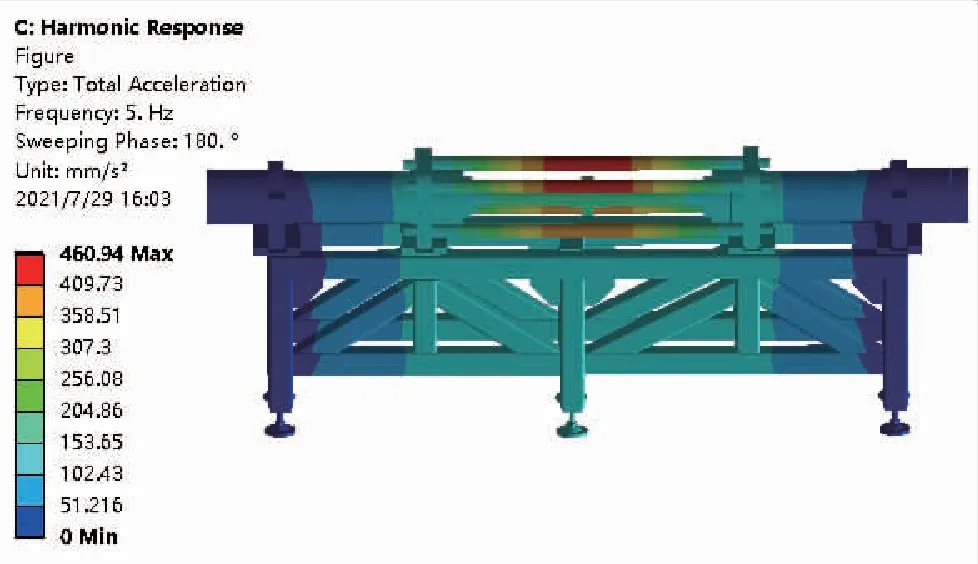
图10 总体加速度响应Fig.10 Total acceleration response

如图11所示，与总体加速度响应不同，在横向加速度响应a上， 试验台上半部分的加速度载荷主要集中在拉杆，上侧2根拉杆远大于下侧2根，第二大的加速度载荷分布在底部支架的各个钢管上，且右侧第2根钢管处最大，而液压缸、活塞盖、导套等承载的横向加速度载荷普遍较小。试验台上部的物理结构除了拉杆，其他部件加速度载荷值均远小于下部，可见拉杆的横向加速度值直接从中间传递到边缘再传递到下方右侧第2根钢管，在底部支架的结构中，中间钢管和底部钢管、右侧斜钢管和底部脚座的加速度载荷值相近，且前者小于后者，右侧钢管加速度值小于以上四者。由此可以推算出横向振动传递的主要路径为：上拉杆→下拉杆→右侧第2根钢管→压板底座→右侧斜钢管、中间脚座→右斜钢管、中间钢管→右钢管；次要振动传递的路径为：活塞盖→液压缸→导套→联轴器。

通过谐响应分析可知，双缸互拉或双缸对顶的加载方式均在两侧液压缸产生无杆腔压力，将此压力作为激励信号可以计算出位移和加速度的分布情况；另外，此压力可以模拟出加载系统工作时所产生的加载力，由此推算出的位移与扫描频率的非线性关系、横向加速度载荷传递路径可分别为试验台的加载频率控制和减振措施提供有效的数值依据，从而避免由于加载而产生共振现象。

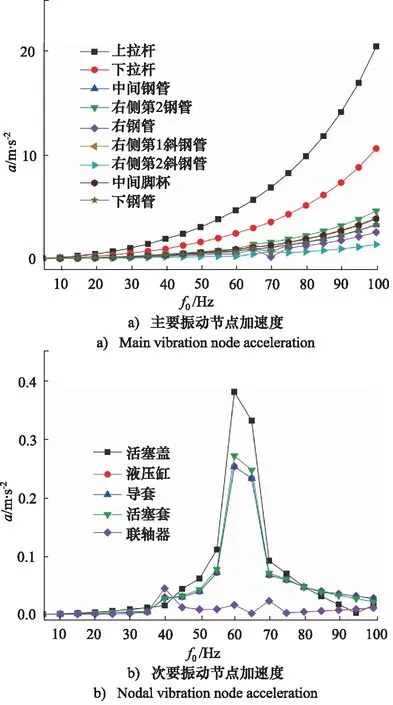
图11 谐响应分析加速度响应Fig.11 Acceleration harmonic response analysis

5 结论

(1) 采用有限元网格划分软件Hypermesh对试验台的整体结构进行了网格划分，并定义了材料属性，通过有限元分析软件ANSYS Workbench进行了静力学仿真分析，仿真结果表明，朝向缸筒的缸内压力方向更合理，且最大应力和应变均发生在两液压缸的连接处，最大应力为109 MPa，小于结构钢的屈服强度，满足设计要求；

(2) 采用有限元分析软件ANSYS Workbench的modal模块对试验台进行了模态分析，仿真结果表明，影响试验台振动的主要模态为一、二、三、四阶模态，而在实际加载过程中，影响试验台整机振动的主要模态为一阶模态，固有频率为40.764 Hz，最大振幅为50.939 mm；

(3) 将第四阶固有频率作为扫描频率变化范围，分别进行了位移谐响应分析和加速度谐响应分析，根据模态分析结果选取若干关键节点，获得了位移、加速度响应的分布情况，从试验台的振幅变化、频率变化、振动传动路径结果等可知，试验台加载试验中，将加载力的频率控制在35 Hz以内，可以避免由于加载而产生试验台共振现象。