越野车半主动悬架的变论域模糊PID控制

潘乾鹏， 周 龙， 吕宝占， 王禹龙

(河南理工大学 机械与动力工程学院， 河南 焦作 454003)

引言

悬架是车辆的重要组成部分，其性能的好坏影响着车辆的行驶平顺性。目前，应用到车辆的悬架大多是被动悬架，刚度和阻尼经过设定后固定不变，无法满足路面激励和工况变化时的性能需求[1]。

半主动悬架是在被动悬架基础上添加阻尼力调节装置形成的，具有较大的可控力值范围，其性能接近主动悬架而且耗能较低、鲁棒性较强[2]。利用PID控制[3]、模糊控制[4]、滑模控制[5]、最优控制[6]以及神经网络控制[7]等方式调节半主动悬架系统的阻尼力，可以使悬架系统更好地适应实际路况，发挥最佳的减振性能。

近些年，以模糊控制和PID控制为基础的控制技术迅速发展。董炳辰等[8]将增量式算法与PID控制器结合，改善了半主动悬架系统的性能，提高了工程车辆的行驶平顺性和操作稳定性。BASHIR A O等[9]采用粒子群优化算法整定PID滑模控制器(SMC-PID)的参数，改善了控制器的效果，提高了磁流变减振器的性能。程自力等[10]采用模糊控制策略，在怠速工况和启动工况下，对发动机磁流变悬置系统的振动特性进行仿真分析，相较于被动悬置，模糊控制的磁流变悬置系统有着较好的隔振性能。李刚等[11]建立1/4车辆半主动悬架系统模型，采用模糊LQG控制策略，分别施加正弦激励与随机路面激励进行仿真，并与被动悬架进行对比分析。BHARDAWAJ S等[12]提出模糊控制和果蝇优化混合控制策略，调节轨道车辆半主动悬架系统的可控阻尼力。胡国良等[13]基于五自由度人体座椅悬架系统模型，采用模糊ANFIS-PID复合控制策略，改善了人体座椅悬架系统的隔振效果。

由于模糊PID控制器的论域范围通常是不变的，其精度容易受到模糊论域的影响。因此，根据设计的阻尼可调两级压力式油气悬架，分析悬架系统的力学特性，建立半车半主动悬架动力学模型，基于变论域理论，实现模糊PID控制器输入和输出论域的自适应调节。在MATLAB/Simulink中构建半车半主动悬架控制模型，分别施加随机路面和冲击路面激励，以车身垂直加速度、车身俯仰角加速度、悬架动挠度和轮胎动载荷为评价指标进行仿真，并与被动悬架和模糊PID控制悬架的性能进行对比分析。

1 悬架系统力学模型

油气悬架主要利用液压传动油来传递系统压力，利用氮气作为弹性物质，有良好的压缩性能[14]。图1所示的两级压力式油气悬架由内置高压气室C、外置低压气室D、单向阀组和节流阀等部分组成，其中蓄能器D腔和E腔之间由橡胶隔膜隔开。通过调节单向阀组和节流阀的过流面积，可以改变悬架系统阻尼力的大小。

压缩行程中，A腔的体积增大，压力减小，油液由B腔经过阻尼孔、节流阀和单向阀组流入A腔和E腔，压力气室气体被压缩，浮动活塞向下移动。载荷较小时，只有低压气室发挥作用，载荷较大时，两级气室同时发挥作用。复原行程中，A腔的体积减小，压力增大，单向阀组关闭，一部分油液由A腔经过阻尼孔回流到B腔，一部分油液由蓄能器E腔经过节流阀回流到B腔平衡缸内压力，工作原理与压缩行程相同。

1.1 刚度模型

考虑到两级气室内氮气的真实气体状态，用RK状态方程来描述油气悬架的刚度特性：

(1)

式中，p—— 气室气体压力

R —— 通用气体常数

T—— 实际气体绝对温度

Vm—— 气体摩尔体积

a—— 气体分子间引力修正系数

b—— 气体体积修正系数

油气悬架系统的缸筒支撑着车身，假设缸筒不动，活塞杆相对于缸筒往复运动[15]。空载状态下，只有低压气室发挥作用，活塞与缸筒之间的相对位移为x1，推导出油气悬架系统的弹性力：

(2)

N1=pd0Vd0+ms1gx1

(3)

式中，M—— 气体摩尔质量

m—— 气体质量

ms1—— 只有低压气室发挥作用时单悬架的簧载质量

g—— 重力加速度

A1—— B腔有效工作面积

pd0—— 低压气室初始压力

Vd0—— 低压气室初始体积

满载状态下，低压气室和高压气室同时发挥作用，平衡时2个气室压力相同。假设活塞与缸筒之间的相对位移为x2，推导出油气悬架系统的弹性力：

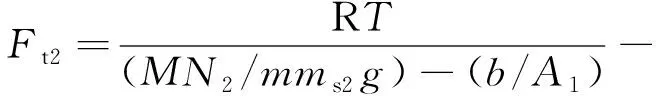
(4)

N2=pd0Vd0+pc0Vc0+ms2gx2

(5)

式中，ms2—— 两级气室同时发挥作用时单悬架的簧载质量

pc0—— 高压气室初始压力

Vc0—— 高压气室初始体积

1.2 阻尼模型

油气悬架系统的阻尼力主要来源于：密封件之间的黏性摩擦力和库伦摩擦力，工作过程中，悬架系统处于颤振状态，润滑良好，摩擦力可忽略；油液流经阻尼阀系产生的主要阻尼；油液流经橡胶油管产生的压力损失[16]。

阻尼孔和单向阀孔口为薄壁孔，节流阀孔口为细长孔。油气悬架系统的参数如表1所示，忽略缸筒与活塞间的摩擦、油液的可压缩性和油液温度变化等因素[17]，推导出悬架系统整个工作行程的流量为：

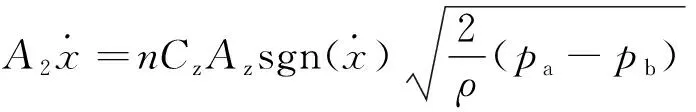
(6)

(7)

式中，A2—— A腔有效工作面积

Cz—— 阻尼孔孔口流量系数

Az—— 阻尼孔过流面积

pa—— A腔瞬时压力

pb—— B腔瞬时压力

Cd—— 单向阀孔口流量系数

dd—— 单向阀过流直径

pe—— E腔瞬时压力

ρ—— 油液密度

dj—— 节流阀过流直径

μ—— 油液动力黏度

lj—— 节流阀过流长度

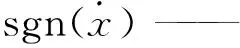
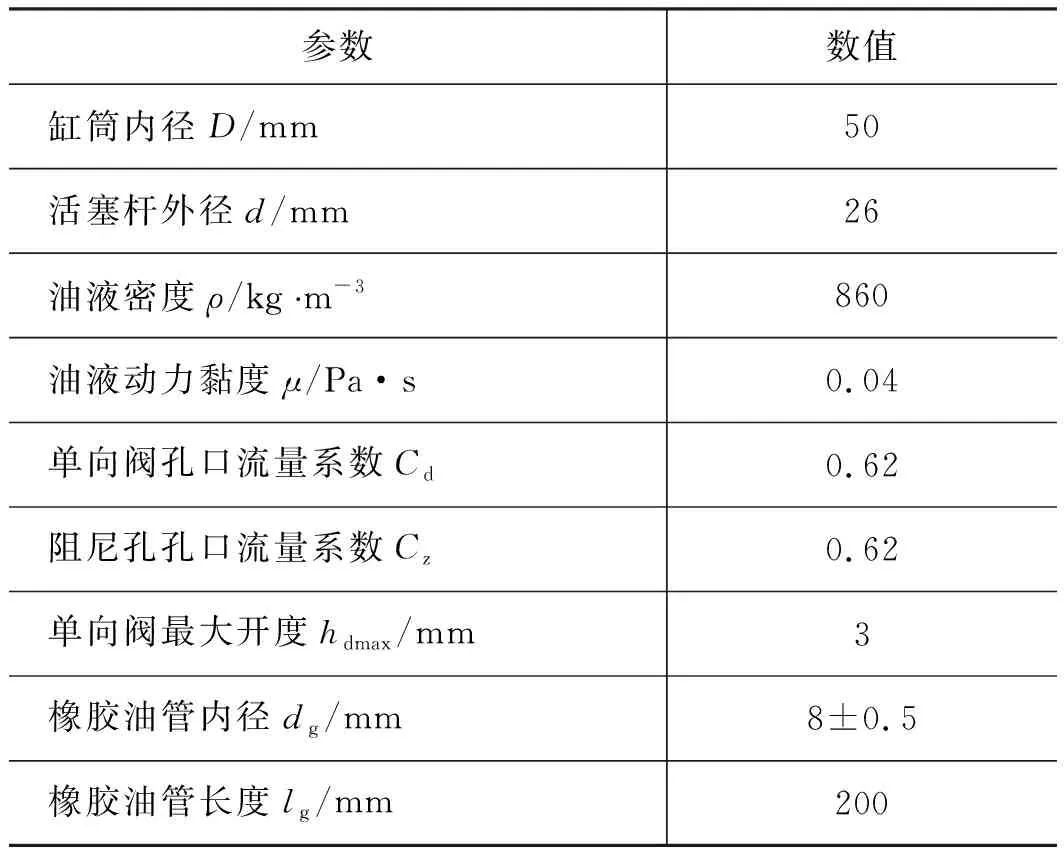
表1 悬架系统参数Tab.1 Parameters of suspension system

令：

代入式(6)和式(7)可以得到，油液流经阻尼阀系的过程中，悬架系统产生的阻尼力为:

(8)

当油液从B腔和蓄能器E腔流入橡胶油管或者从橡胶油管流入B腔和蓄能器E腔时，油液的过流面积突然发生变化，产生局部压力损失引起的阻尼力[18]为：

1.2 主要仪器及试剂 采用免疫印迹法检测Furin的蛋白表达水平。主要仪器有Trans-Blot SD Semi-Dry半干转膜仪(Bio-Radshang分子量Marker(NEB公司，美国)；电泳仪及电泳槽(Bio-rad公司，美国)；VC13OPB型超声波震碎仪(Sonies公司，美国)；Cocktail (Roche公司，德国)；Furin抗体(Santa Cruz Biotechnology公司，美国)；1N NaOH(Sigma公司，美国)、MTT和山羊抗兔和山羊抗鼠二抗；BCA蛋白质定量试剂盒(Pierce公司，美国)。

(9)

式中，Ag—— 橡胶油管截面积。

油液在橡胶油管中流动会产生沿程压力损失，油液从悬架B腔出口处流动到蓄能器E腔入口处的压力损失引起的阻尼力[16]为：

(10)

式中，lg—— 橡胶油管长度

dg—— 橡胶油管内径

将式(8)～式(10)相加，可以得到油气悬架系统的总阻尼力：

fz=fb+fc1+fc2

(11)

2 半车半主动悬架动力学模型

图2所示是利用集中质量法建立的半车半主动悬架模型，该模型具有车身垂直振动、前车轮垂直振动、后车轮垂直振动和车身俯仰振动4个自由度。

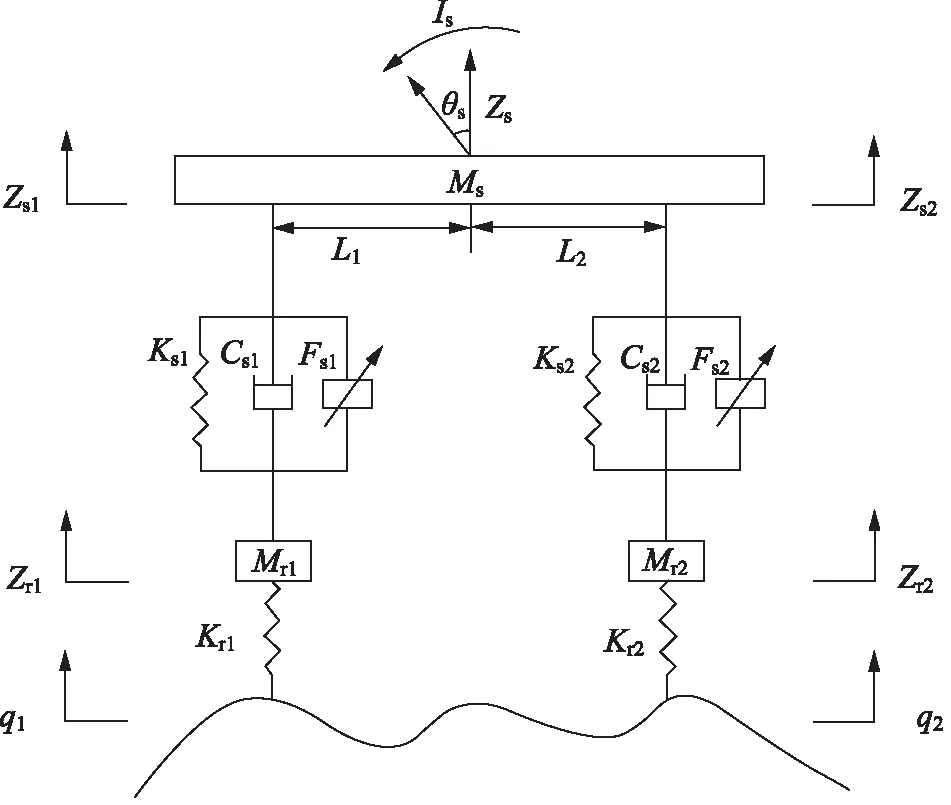
图2 半车半主动悬架模型Fig.2 Semi-active suspension model of semi-vehicle

对半车半主动悬架模型进行受力分析，车身质心运动微分方程为：

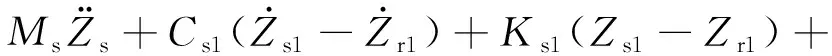
(12)

前、后悬架非簧载质量运动微分方程为：

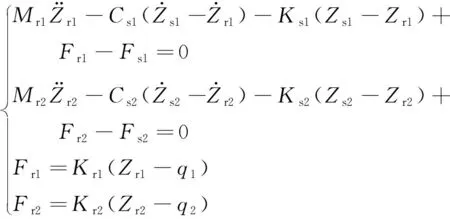
(13)

车身俯仰运动微分方程为：

(14)

前、后悬架垂直加速度与车身质心加速度、俯仰角加速度之间的关系为：

(15)

前、后悬架车身动挠度与车身绝对位移、非簧载质量绝对位移之间的关系为：

(16)

式中，Ms—— 簧载质量

Zs—— 车身质心绝对位移

Zs1,Zs2—— 前、后悬架车身绝对位移

Cs1,Cs2—— 前、后悬架系统阻尼系数

Ks1,Ks2—— 前、后悬架系统等效刚度

Zr1,Zr2—— 前、后悬架非簧载质量绝对位移

Fs1,Fs2—— 前、后悬架系统产生的可调阻尼力

Mr1,Mr2—— 前、后悬架非簧载质量

Fr1,Fr2—— 前、后车轮动载荷

Kr1,Kr2—— 前、后车轮等效刚度

q1,q2—— 前、后悬架处的路面激励

L1,L2—— 前、后轮与车身质心之间的距离

Is—— 车身转动惯量

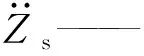
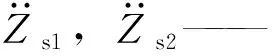
Zd1,Zd2—— 前、后悬架车身动挠度

3 半主动悬架变论域模糊PID控制器

在模糊控制器中，模糊规则、比例因子和变量基本论域通常是预先设定的，固定的变量基本论域直接影响着模糊PID控制器的性能[19]。因此，结合变论域理论，在模糊PID控制器的基础上增加变论域控制器，通过选择合适的论域伸缩因子，使得输入和输出变量的基本论域能够根据系统误差变化实时伸展或收缩。

变论域模糊PID控制器发出指令， 通过调节油气悬架系统中节流阀和单向阀的过流面积，改变悬架系统阻尼力的大小， 变论域控制器和模糊控制器都采用两输入三输出的二维控制器，如图3所示。

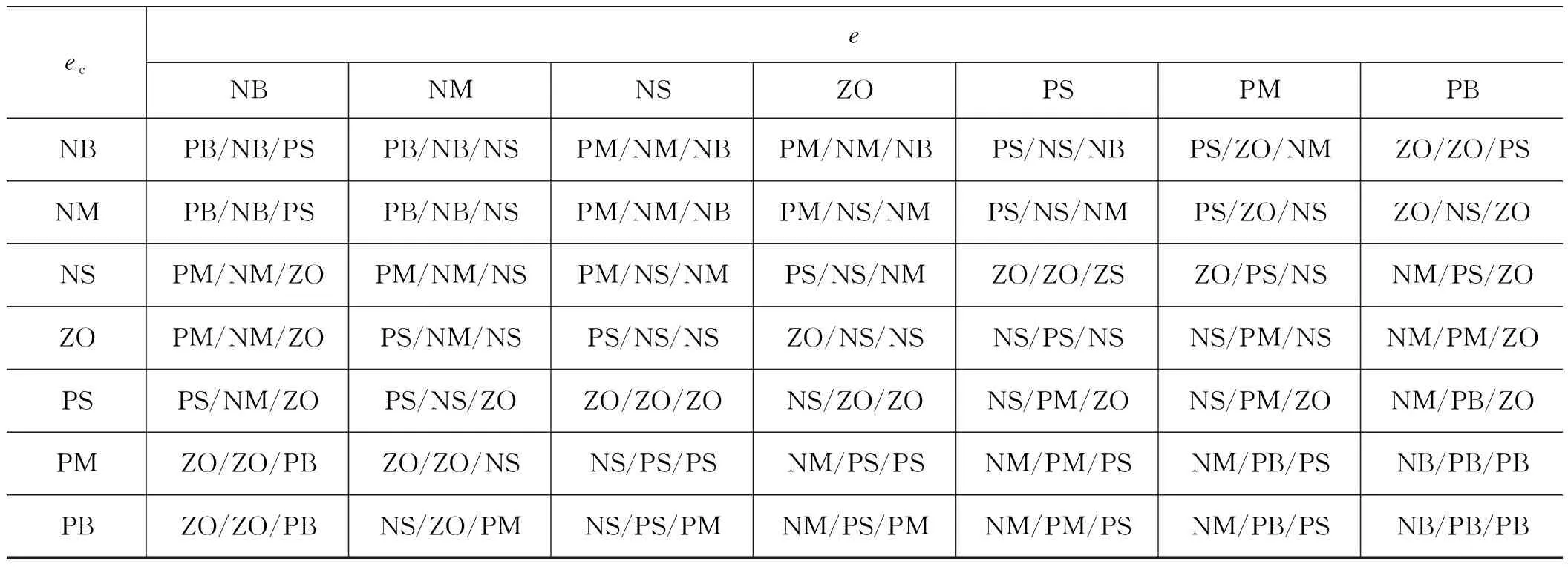
表2 ΔKp，ΔKi，ΔKd的模糊控制规则Tab.2 Fuzzy control rules of ΔKp,ΔKi and ΔKd

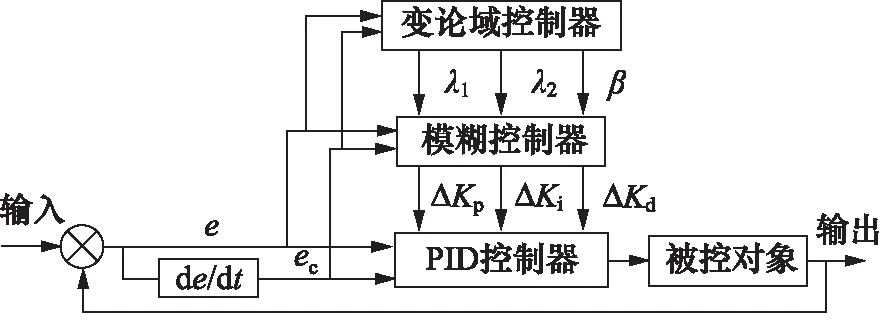
图3 变论域模糊PID控制结构Fig.3 Structure of variable universe Fuzzy PID control

选取车身速度与参考值(取0)的偏差e和偏差变化率ec为输入变量，假设变论域控制器中输入变量X的基本论域为[-E，E]，输出变量Y的基本论域为[-U，U]，可以得到变量伸缩因子的论域公式：

(17)

式中，λ1，λ2—— 偏差e和偏差变化率ec的伸缩因子

β—— 输出变量的伸缩因子

通过制定相应的模糊规则来优化PID控制器的参数，修正后的PID参数值为：

(18)

式中，Kp，Ki，Kd—— PID最终参数设定值

Kp0，Ki0，Kd0—— PID初始参数设定值

ΔKp，ΔKi，ΔKd—— 模糊修正值

变论域控制器中偏差e的基本论域为[-0.2，0.2]，偏差变化率ec的基本论域为[-2，2]，伸缩因子的基本论域均为[0，1]。分别选用5个模糊子集来描述偏差、偏差变化率和变量伸缩因子，即负大(NB)、负小(NS)、零(ZO)、正小(PS)、正大(PB)，变量的模糊论域均取为[-1，1]，其模糊子集为[NB，NS，ZO，PS，PB]。

模糊控制器中变量的基本论域是随着变论域控制器的调整而变化的，设计模糊控制器时只需要考虑变量的模糊论域。分别选用7个模糊子集来描述变量，即负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB)。变量的模糊论域均取为[-1，1]，其模糊子集为[NB，NM，NS，ZO，PS，PM，PB]。

考虑到控制系统的滞后性，要尽量缩短计算时间，偏差e和偏差变化率ec的隶属函数选用Gaussmf函数，输出变量的隶属函数选用Trimf函数。模糊推理方法采用Mamdani法，模糊判决采用重心法，模糊控制器的控制规则如表2所示，变论域控制器的控制规则如表3所示。

图4 半车半主动悬架控制模型Fig.4 Control model of semi-active suspension of semi-vehicle

4 系统仿真及结果分析

考虑到相同路面激励下，越野车空载状态下的行驶平顺性较差。利用MATLAB/Simulink建立半车半主动悬架变论域模糊PID控制模型，对空载状态下越野车的行驶平顺性进行仿真。

选取的某越野车参数如下：车身簧载质量为1980 kg，车身俯仰转动惯量为3779 kg·m2，前轮非簧载质量为94.5 kg，后轮非簧载质量为122.5 kg， 轮胎等效刚度系数为207500 N/m，前轴距车辆质心距离为1.241 m，后轴距车辆质心距离为1.559 m。

4.1 冲击路面激励仿真

越野车行驶的实际路面中存在减速带、坑洼路面以及凸块路面等，车轮与障碍物的撞击会使车身产生明显晃动[20]，进而影响越野车的行驶平顺性。

以凸块路面为例，考虑到越野车前轮与后轮之间的滞后量，可以得到越野车前、后轮经过凸块路面的数学模型：

式中，q1—— 前轮路面激励

Hr—— 凸块路面高度

u—— 车辆行驶速度

Lr—— 凸块路面长度

(20)

式中，q2—— 后轮路面激励

Δt—— 滞后量，Δt=Lz/u

Lz—— 车辆轴距

假设越野车行驶速度为30 km/h，以凸块路面作为输入激励，对半车半主动悬架控制模型进行仿真，仿真时间为6 s。图5为凸块路面激励下悬架系统的响应曲线，表4为凸块路面激励下悬架系统的性能参数。

由图5仿真结果分析，在凸块路面激励下，变论域模糊PID控制悬架相较于被动悬架和模糊PID控制悬架，曲线的波动范围最小，最先趋于平衡，其减振性能较好。

与模糊PID控制相比，采用变论域模糊PID控制，越野车前、 后车身加速度和车身俯仰角加速度的均方根分别减小30.89%,34.36%,37.00%，越野车前、 后车轮动载荷的均方根分别减小18.21%,12.62%，越野车前、后车身动挠度的均方根比较接近。综合来看，变论域模糊PID控制悬架的性能明显优于模糊PID控制悬架，有效提高了越野车的行驶平顺性。

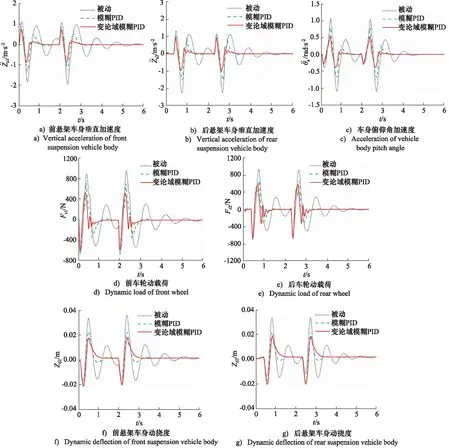
图5 凸块路面激励下悬架系统的响应曲线Fig.5 Response curve of suspension system under excitation of convex block pavement

4.2 随机路面激励仿真

建立随机路面输入模型要考虑前后轮输入的滞后性，采用滤波白噪声法，考虑路面截止频率，建立前、后轮输入的路面不平度时域模型[21]：

(21)

(22)

式中，qf(t) —— 前轮路面位移

qg(t) —— 后轮路面位移

表4 凸块路面激励下悬架系统的性能参数Tab.4 Performance parameters of suspension system under excitation of convex block pavement

fmin—— 下截止频率，取0.063

n0—— 空间参考频率，取0.1

w(t) —— 滤波白噪声信号

Gq(n0) —— 路面不平度系数

为了进一步验证变论域模糊PID控制策略的有效性，以D级路面作为输入激励，车速取30 km/h，仿真时间为6 s，对半车半主动悬架控制模型进行仿真。图6为D级随机路面激励下悬架系统的响应曲线。

由图6分析，D级路面激励下，被动悬架的车身质心加速度波动范围为[-0.8181，0.7647]，均方根为0.3274 m·s-2；模糊PID控制悬架的车身质心加速度波动范围为[-0.4903，0.5689]，均方根为0.2016 m·s-2；变论域模糊PID控制悬架的车身质心加速度波动范围为[-0.4676，0.4933]，均方根为0.1710 m·s-2。被动悬架的车身俯仰角加速度波动范围为[-0.7599，0.9249]，均方根为0.3093 rad·s-2；模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.5116，0.6582]，均方根为0.1857 rad·s-2；变论域模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.4155，0.5417]，均方根为0.1469 rad·s-2。

与被动悬架相比，变论域模糊PID控制悬架的车身质心加速度和车身俯仰角加速度的均方根分别减小47.77%和52.51%，与模糊PID控制悬架相比，变论域模糊PID控制悬架的车身质心加速度和车身俯仰角加速度的均方根分别减小15.18%和20.89%。

4.3 控制系统的时滞分析

半主动悬架控制系统存在的时滞主要是控制器信号传输过程中的时滞[22]，导致油气悬架系统可控阻尼力的不同步，甚至会导致控制系统失稳，降低悬架系统的减振性能，进而影响越野车的行驶平顺性。因此，施加D级路面激励，仿真时间为6 s，通过比较车身质心加速度和车身俯仰角加速度来分析时滞对控制系统的影响。

图7为采用变论域模糊PID控制时，不同时滞量悬架系统的响应曲线。时滞量越大，变论域模糊PID控制器的控制效果越差。时滞为0.15 s时，车身质心加速度波动范围为[-11.73，11.45]，均方根为3.474 m·s-2，车身俯仰角加速度波动范围为[-3.446，3.662]，均方根为1.167 rad·s-2，相较于无时滞的变论域模糊PID控制悬架，车身质心加速度和车身俯仰角加速度的均方根分别增大1931.58%和694.42%，车身质心加速度和车身俯仰角加速度的波动幅度较大。

图6 D级随机路面激励下悬架系统的响应曲线Fig.6 Response curve of suspension system under excitation of class D random road

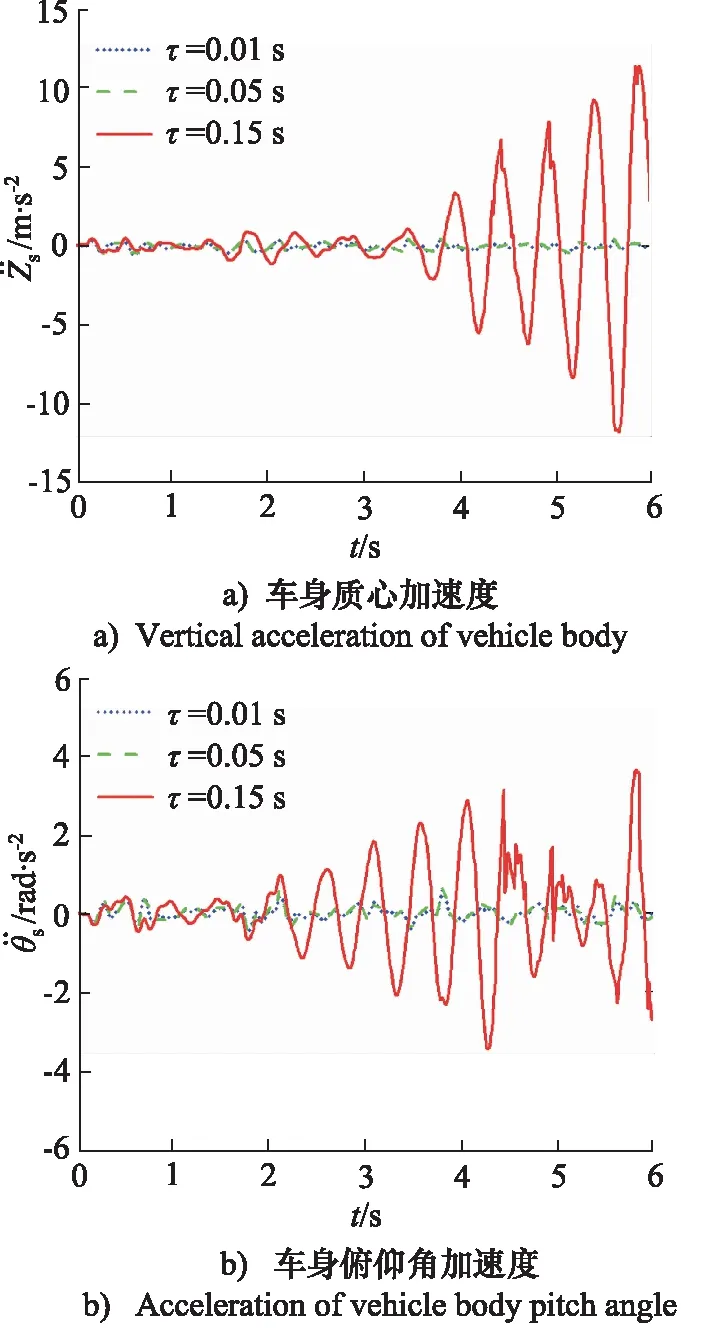
图7 不同时滞量悬架系统的响应曲线Fig.7 Response curves of suspension systems with different time delays

时滞量一定时，采用的控制策略不同，优化的效果有所差异。以时滞量为0.01 s和0.05 s为例，采用变论域模糊PID控制和模糊PID控制，比较车身质心加速度和车身俯仰角加速度的波动范围和均方根。图8和图9为时滞量分别为0.01 s和0.05 s时，2种控制策略下悬架系统的响应曲线。

由图8分析，时滞量为0.01 s时，模糊PID控制悬架的车身质心加速度波动范围为[-0.5563，0.6488]，均方根为0.2087 m·s-2，变论域模糊PID控制悬架的车身质心加速度波动范围为[-0.4980，0.5279]，均方根为0.1816 m·s-2；模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.5186，0.6707]，均方根为0.1918 rad·s-2，变论域模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.4408，0.5672]，均方根为0.1543 rad·s-2。与模糊PID控制悬架相比，变论域模糊PID控制悬架车身质心加速度和车身俯仰角加速度的均方根分别减小12.98%和19.55%。

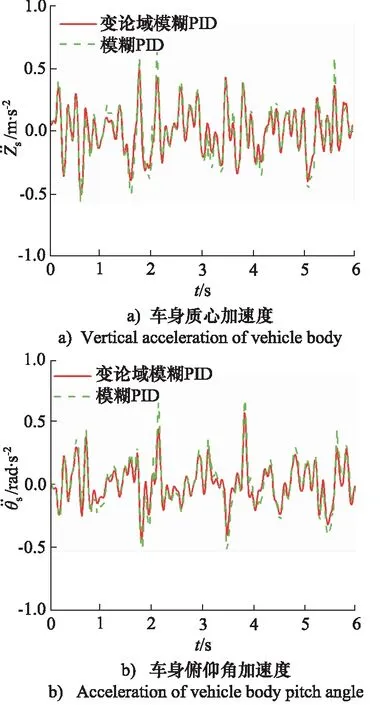
图8 τ=0.01 s，2种控制策略下悬架系统的响应曲线Fig.8 Response curves of suspension system under two control strategies when τ=0.01 s

由图9分析，时滞量为0.05 s时，模糊PID控制悬架的车身质心加速度波动范围为[-0.7001，0.7554]，均方根为0.2420 m·s-2，变论域模糊PID控制悬架的车身质心加速度波动范围为[-0.7052，0.7274]，均方根为0.2402 m·s-2；模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.5861，0.7343]，均方根为0.2229 rad·s-2，变论域模糊PID控制悬架的车身俯仰角加速度波动范围为[-0.5511，0.6428]，均方根为0.1926 rad·s-2。与模糊PID控制悬架相比，变论域模糊PID控制悬架的车身质心加速度和车身俯仰角加速度的均方根分别减小0.74%和13.59%。

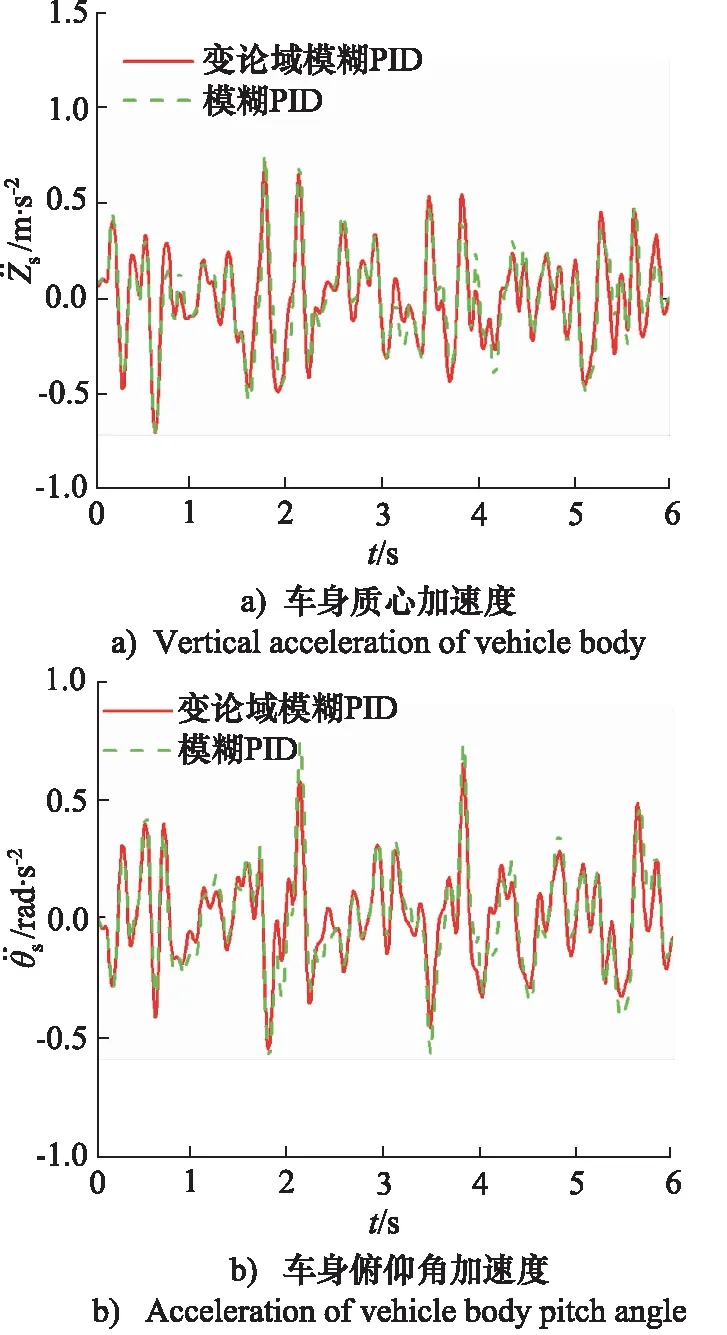
图9 τ=0.05 s，2种控制策略下悬架系统的响应曲线Fig.9 Response curves of suspension system under two control strategies when τ=0.05 s

综合分析可得，半主动悬架控制系统的时滞量处于稳定范围时，采用变论域模糊PID控制明显优于模糊PID控制，时滞量过大，控制系统失稳，影响悬架系统的减振性能。

5 结论

为了改善越野车的行驶平顺性，根据阻尼可调两级压力式油气悬架的力学特性，建立半车半主动悬架动力学模型，在MATLAB/Simulink中建立变论域模糊PID控制模型，分别施加冲击路面和随机路面激励进行仿真分析。

(1) 在2种路面激励下，采用变论域模糊PID控制对越野车行驶平顺性均有一定程度的优化，在冲击路面激励下优化效果较好；相较于被动悬架，变论域模糊PID控制悬架的前、后车身垂直加速度和车身俯仰角加速度均方根分别减小60.93%，61.31%，61.57%；相较于模糊PID控制悬架，变论域模糊PID控制悬架的前、后车身垂直加速度和车身俯仰角加速度均方根分别减小30.89%，34.36%，37.00%，能够进一步改善悬架的性能，提高越野车的行驶平顺性；

(2) 时滞的存在影响着半主动悬架控制系统的性能，时滞量处于稳定范围时，采用变论域模糊PID控制明显优于模糊PID控制；时滞量越大，半主动悬架控制系统受到的影响也就越大，甚至会导致控制系统失稳。