一枝独秀不如百花齐放——高中数学多元化教学研究

◎施良结 (福建省晋江市永和中学，福建 晋江 362235)

一、高中数学教学中实施多元化教学的意义

(一)满足学生多样性学习需求

多元化教学不是为了多元而多元，而是基于学生多样性学习需求的多元.众所周知，一刀切的数学教学模式忽视了学生个体的差异性，不能真正地挖掘学生的学习潜能，也不能有效地培育学生的数学核心素养.对此，教师摒弃一刀切的灌输模式，积极设计多元化教学模式，既能为“因材施教”这一古老的教育理念注入新的活力，又能使每位学生找寻到适合自己的角色，从而满足了学生多样性的学习需求.

(二)有助于学生发现数学之美

数学课堂不只是数学题、数学符号、数学卷子，还有美丽的图案、精致的模型、高妙的智慧……作为数学教师的我们，有责任也有义务引导学生发现数学的美.如何做到这一点呢？须知，多元化教学模式一改传统题海战术的单调乏味，融合了多种新的元素、新的资源.教师设计多元化教学模式，不仅能激活数学教学之活力，还能使数学教学变得多姿多彩，美不胜收.鉴于此，高中数学教师应当瞄准多元化教学模式，并将之化为实际行动，从而使学生在数学的乐园中进行一次次寻美之旅.

二、多元化教学在高中数学教学中的运用实践

(一)教学方法的多元化

1.利用启发式教学法，构建智慧化课堂

把启发式教学法引入数学教学中，不仅能锻炼学生的数学思维，还能激活学生的数学智慧.基于这一情况，高中数学教师应当主动地利用启发式教学法，以此来使学生挖掘数学中的智慧.例如，教师在引导学生学习《三角恒等变换》这一知识的时候，就利用了启发式教学法.首先，教师启发学生自行梳理本节课要学习的几个关键知识点.在教师的启发下，学生找出了如下几个要点：①两角和与差的正弦、余弦公式；②二倍角的正弦、余弦公式；③辅助角公式.其次，教师引导学生分析“三角函数式的化简与求值”.教师启发：“在化简求值的过程中我们要遵循三看的原则.你们说一说是哪三看呢？”在教师的启发下，学生对“三看”进行分析与解答.有的学生说：“第一要看角，对角进行合理拆分.”有的学生说：“第二要看函数名称，这常常体现在切化弦之中.”还有的学生补充说：“第三点就要看结构特征.”最后，教师引导学生对“给值求值”的这类问题进行分析.等学习了这类问题后，教师启发学生利用同样的方法自行分析“给值求角”的问题.于是，在教师的启发下，学生在“给值求值”与“给值求角”两者之间搭建了一座“转化”的桥梁.

2.利用互动式教学法，构建动感式课堂

教学本应是教与学的双向互动.然而，很多数学教师为了赶进度而忽视了与学生的互动.这就不利于调动学生的参与感.为了解决这一问题，教师应当主动地利用互动式教学方法，构建动感式数学课堂，从而唤醒学生沉睡的思维，使学生动起来.例如，在学习《双曲线及其标准方程》的时候，教师与学生进行了如下互动.【互动一】“关于双曲线的定义”.教师对学生说：“在双曲线的定义中，必须要求常数小于两个定点之间的距离，那么常数等于两个定点之间的距离，或是常数为零的时候，动点的轨迹是怎样的？”于是，有的学生说：“常数等于两个定点之间的距离，此时轨迹是以动点为端点的两条射线.”有的学生说：“常数大于两个定点之间的距离的时候，动点的轨迹是不存在的.”还有的学生补充说：“假如常数为零，那么动点的轨迹为两个定点间的线段长度.”经过这样的互动，学生对双曲线的定义产生了全面的认识.【互动二】“双曲线的标准方程”.教师对学生说：“对于双曲线的标准方程，我们应该注意哪些呢？”于是，有的学生说：“焦点跟着正项走.假如x平方这一项的系数为正，那么焦点会在x轴上；假如y的平方这一项的系数为正，那么焦点会在y轴上面.”而后，其他学生也分别表达了自己的看法.【互动三】双曲线定义的应用.在这一环节中，教师与学生就“与双曲线有关的轨迹问题、如何求双曲线的标准方程”等内容进行了积极互动.通过这么几轮的互动，学生对双曲线有关内容产生了深刻的印象.

3.利用留白式教学法，构建探究型课堂

很多时候，教师在教学中讲得过多.这在使学生获得大量知识的同时也加大了他们的学习负担.久而久之，学生失去了自我思考的空间.为了使学生获得应有的自我思考空间，教师不应该讲得过多，而应该学会留白.如此一来，这在给予学生自由的同时还能促进探究型数学课堂的构建.例如，在学习《平面向量的概念》这一内容的时候，教师没有直接告诉学生什么是平面向量的概念，而是留下悬念留出空白，让学生对这一概念的具体内容进行自主探究.【留白一】在物理之中，位移与速度都是既有大小又有方向的量.那么，在数学中能不能对这些量展开抽象，构成一种新的量呢？【留白二】数轴可以表示数量，那么如何表示向量呢？有向线段包含了哪些元素呢？【留白三】平行向量与相等向量具有哪些差异？这些“留白”一下子激发了学生对于平面向量有关内容的探究欲望.于是，学生对教材中的有关向量的概念这一节进行了深度解读，并在解读的过程中认真地研究了平面向量的特点、本质.几分钟过后，教师让一些学生说一说他们是如何填补这些“留白”的.在进行发言的过程中，大多数学生都充分地说出了他们对平面向量有关内容的独特理解.由此可见，留白的方式不仅使学生自主地填补了知识上的“空白”，还在一定程度上锻炼了他们的数学思维活跃度.

4.利用情境化教学法，构建活泼型课堂

各种各样的教学情境犹如万花筒，不仅能够使课程教学变得丰富化多彩化，还可以点燃大多数学生的学习热情，从而促进活泼型课堂的构建.考虑到情境化教学所具有的这样的优势，数学教师应该自觉地改变课堂教学之中没有情境或者缺少情境的状态，把有效的情境带入到课堂教学之中，从而使情境发挥“火焰”的效果，进而点燃学生学习热情、探究热情、思考热情之火焰.

例如，在讲授《简单几何体的表面积与体积》这一内容的时候，教师就创设了一些有助于点燃学生学习热情的情境.首先，教师对学生说：“同学们，我们先来看几组图片情境，在观看的过程中请大家说一说你们所观察到的几何体的名称.”话音刚刚落下，教师就立即利用电子白板向学生播放了一些简单几何体的图片.在对这些图片情境进行观察的过程中，学生不由自主地说出了这些图形的名称.有的学生说：“第一张图片展示的是棱柱.”有的学生说：“第二张图片展示的是棱台.”还有的学生说：“第三张图片展示的是棱锥.”然后，教师对学生说：“在这些图片情境之中，我们发现了一些立体化的几个图形.它们各有各的特点.刚才大家对这些图形的名称进行了回答.你们说得很好.”而后，教师创设了一些问题情境：“大家知道什么是几何体的表面积吗？对于棱柱、棱台、棱锥，你们知道如何计算它们的表面积吗？”于是，在问题情境的启发下，大多数学生就几何体的表面积的概念进行了思考.几分钟过后，学生基于之前的学习经验与知识积累得出了如下结论：围成多面体的各个面的面积之和.接着，教师创设了同桌讨论的情境：请同桌之间就如何计算棱锥、棱台的表面积进行探究与讨论.在这个过程之中，同桌之间就多面体表面积的突破口、切入点、计算步骤等信息进行了研讨.最后，教师创设了“竞赛”情境.在这个情境之中，谁先算出多面体的表面积谁就获得一分.为了获得更多的分数，所有学生都聚精会神地进行观察，兵贵神速地进行计算.这样的竞赛情境瞬间激发了学生的学习劲头.由此可见，这些情境的创设既使数学课堂的氛围变得活泼，又使学生对多面体的表面积产生了深刻认识.

(二)教学资源的多元化

1.巧借微课资源，促进学生高效学习

微课具有直观形象，短小精悍的特点.把微课这一资源运用到数学教学之中，既能使学生获取丰富的学习资料，还能提升学生的学习效率.为此，教师应该巧借微课资源，促使学生进行高效学习.例如，在讲授《平面向量基本定理》这一内容的时候，教师就充分地发挥了微课的优势.首先，让学生利用微课进行自主预习.在观看微课的时候，学生有效地预习了本节内容，并了解了基底、基向量等概念，在此基础上，还制作了重点突出的预习清单.其次，教师利用微课讲解了“向量的分解”这一难点.由于这节微课设计得精准到位，结合了最典型的例题，所以，在倾听的过程中，学生对这一难点知识产生了透彻的理解.再次，教师还向学生提供了《小试牛刀之平面向量基本定理》的微课.这里面有不同难度的练习题.学生根据自身的掌握情况选择适合自己的练习题进行操作.总之，微课在数学教学中的全面运用，有效地提升数学教学的针对性，也使学生获得了事半功倍的学习体验.

2.利用导学案，培育自主学习能力

导学案犹如方向盘，对学生具有引路的作用.教师在高中数学中巧妙地运用导学案，不仅能使学生少走一些弯路，也能使学生获得更多的自由.例如，在学习《平面向量的应用》这一课的时候，教师就为学生设计了导学案.在这份导学案中，学生可以看到如下内容.【学习清单】①能够自行总结向量应用的常用结论.②掌握向量应用的分类概述.③分析向量的具体应用.【学法指引】在这一环节中，教师做出了如下提示与指引：①利用向量解决平面几何问题.②向量在物理中的运用.③向量与三角形的结合.④向量在函数不等式中的运用.【我的收获】谈一谈你从本节中收获了哪些数学知识或数学思想.在导学案的引导下，学生自主探究了《平面向量的应用》有关内容.

3.引入思维导图，激活学生数学思维

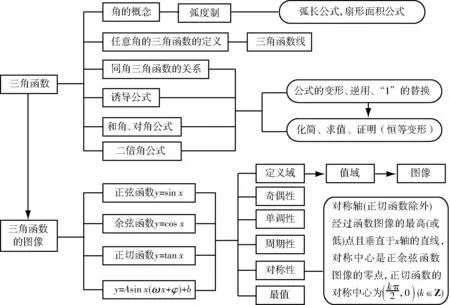
数学教学的主要任务之一是唤醒学生沉睡的思维.如何唤醒呢？依靠灌输知识的方式肯定是行不通的.对此，教师可以引入思维导图这一资源.在绘制思维导图的过程中，学生的思维能够发生由点到面的转化.如此一来，具有系统性的知识体系在学生的脑海中得以诞生.例如，学习了《三角函数》这一内容后，教师让学生利用思维导图总结归纳本节重点内容.于是，学生从学习实际出发，从教材中提炼了若干个知识点，绘制了有关本课的思维导图.这一导图包含了“角的概念、任意三角函数的定义、诱导公式”等几个分支，并把相关的具体内容附加在了分支的旁边.此外，每个分支都有对应的典型例题以及变式题.这样的思维导图使学生对三角函数产生了系统化的认知.

(三)教学评价的多元化

1.教师点评，精准到位

教师的点评具有激励、引导、启发等作用.在对学生进行点评的时候，教师应当掌握点评的艺术与技巧，使学生在心理上乐于接受.比如说，教师可以利用先扬后抑的方法进行点评.首先，指出学生在回答问题的过程中所展现出的闪光点，而后以转折的方式指出他的不足之处.这样总比直接说出学生的不足要更加人性化.再比如说，教师可以利用一针见血的方式进行点评.这种点评方式摒弃了重复啰唆的弊端，直接切中了最核心最关键的地方，使点评具有了针对性.总之，在点评的过程中，教师要从每位学生的实际情况出发，为学生提供具有建设性的评语，而不是一味地讲一些套话，空话.

2.学生互评，共同进步

评价不仅仅存在于教师与学生之间，还可以是学生与学生之间的互评.这一评价方式具有很多好处.一方面，可以激发学生的学习积极性，提升学生的课堂参与感.另一方面，可以锻炼学生的口语表达能力，也可以使学生获得为人处事的学问.例如，在学习《三角函数的诱导公式》这一内容的时候，教师就实施了学生互评的评价方式.具体如下：首先，教师对学生说：“当局者迷旁观者清.很多时候，自己不能更好地发现自己的问题.但是别人就能够很好地指出自身的问题.所以，倾听别人对自己的评价还是有一定的道理的.下面，咱们就进行互评的活动.”其次，教师让同桌之间相互讨论三角函数的诱导公式，并让同桌之间对彼此的回答情况进行客观公正的相互评价.在同桌进行相互点评的过程中，同桌两人都要分别指出对方的优点与缺点，并相互借鉴对方的优点.有的学生说：“你刚才说得很好.但是，有一个要点漏掉了.如果加上这个要点就更好了.你自己能够想起来是漏掉了哪个要点吗？”有的学生说：“对于你刚才的回答，我听得很认真.一方面，你对三角函数的诱导公式进行了有条有理的归纳；另一方面，你还提出了对三角函数诱导公式的一些独特性看法.这些都是一些闪光点.”还有的学生……如此一来，这样的互评模式既促进同桌双方的共同进步，还增进了双方的情感.

三、结束语

综上所述，数学教学不是面向一个学生或某些学生的教学，而是面向人人的教学.每个学生的实际情况并非一样，他们各有各的特点、各有各的追求.因此，用多元化教学模式取代千篇一律的教学模式是教改的必然趋势.在高中数学教学中，教师应当从学情出发，而不是从考试本身出发；应当真正瞄准学生的学习需求，而不是仅仅关注教学本身.在此基础上，教师还要以多元化的教学方法引导学生自主建构知识，以多元化的教学资源丰富学生的学习体验，以多元化的教学评价激励学生努力上进，从而使学生在获得数学知识的同时还能具备数学核心素养，进而使高中数学教学呈现“春色满园”的盎然之景.