教材一个例子引发的思考——椭圆中一个定值问题

广东省揭阳市揭阳第一中学(522000) 张喜金

课堂教学与反思相辅相成,即要掌握好基础知识基本方法,也在拓展其内在属性,找出看似没关的内容之间的内在联系,更容易让学生掌握并学会应用.

圆锥曲线的“两率”(斜率、离心率)问题是高中数学的重要内容,也是高考命题者的“必争之地”,在高考数学试题中,圆锥曲线中的斜率的积为定值的问题经常亮相,重点考查,已经成为高考数学试题中绕不开的“情结”,值得我们探讨研究.

下面就教材(选择性必修第一册)的例题进行思考:

1 问题探索

例题如图,设A,B两点的坐标分别为A(−5,0),B(5,0).直线AM,BM相交于点M,且它们的斜率之积是求点M的轨迹方程.

思考例题求得点M的轨迹方程为1(x ̸=±5),其轨迹是除去(−5,0),(5,0)两点的椭圆.可见例题是由斜率积得到了椭圆,对于这个具体的椭圆,直观形象的体现了焦点在x轴的上的椭圆上异于左右顶点A,B的任一点M,直线AM,BM的斜率之积是定值简单求法,内蕴十足,那么,对于一般的椭圆=1(a>b>0),是否具备这样的特征?

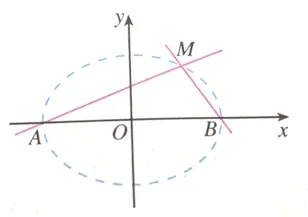
探究椭圆=1(a >b >0) 左右顶点A(−a,0),B(a,0),M(x,y)在椭圆上(异于A,B),则kAM=所以kAM·kBM==

总结由此可以看出,椭圆上异于左右顶点A,B的另一点M与左右顶点连线斜率的乘积为定值,即kAM·kBM=

延伸焦点在y轴上的椭圆=1(a>b>0)也是有相似特征,可得kAM·kBM=其中A,B是上下顶点.

进一步思考:A,B两点是长轴端点,关于原点对称,那是否可以是短轴端点呢? 是否可以是更一般的关于原点对称的椭圆上任两点呢?

结论1设椭圆=1(a>b>0)上关于原点对称的两点A(x1,y1),B(−x1,−y1),P(x0,y0)在椭圆上(异于A,B),且直线PA,PB斜率存在,则kP A·kP B=

证明A(x1,y1),P(x0,y0) 坐标代入椭圆方程得两式作差得即即

结论2焦点在y轴的椭圆=1(a>b>0)上,有

结论1、结论2 得到斜率积为定值,前提条件是A,B关于原点对称或A,B连线过原点,结论如果换成双曲线,同样有相似性质成立.以上这个性质在圆锥曲线问题中起到了化繁为简的作用,使得很多问题的解决变得有章可循,直奔问题的本源.

2 结论应用举例

例1已知椭圆C:=1(a >b >0)的左、右顶点分别为A,B,直线l过点B且与x轴垂直,点P是椭圆C上异于A,B的动点,直线AP与直线l交于点M,若OM⊥PB,则椭圆的离心率是____.

分析注意到题目涉及三个斜率kP A,kP B,kOM,如图所示,则

又因为OM⊥PB,所以

又

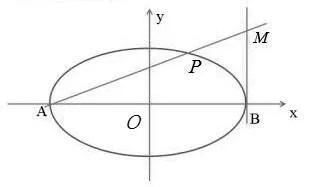
解析由分析①②③可得又kP A=所以所以e==

强化训练1如图,A1,A2为椭圆=1 的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,求|OS|2+|OT|2的值.

分析平行四边形OPQR中,斜率可转移,即直线QA1斜率与直线OS斜率相等,直线QA2斜率与直线OT斜率相等.

解析设Q(x,y),T(x1,y1),S(x2,y2),直线QA1,QA2的斜率分别为k1,k2,则直线OT,OS的斜率分别为k1,k2,由分析可得k1k2=所以|OT|2=x21+k21x21=同理|OS|2=因此

评注问题的本质在于斜率的转移与斜率积为定值,把握住内在规律,化繁为简.

3 联结中点弦问题

结论3由图可知OM//PB,故kOM=kP B,又因为kP A·kP B=所以kP A·kOM=即中点弦问题.

结论4同样的,对于椭圆=1(a >b >0)任意一条弦CD(斜率存在且非零),弦CD的中点为N的时候,则kON·kCD=

荷兰著名数学教育家弗赖登塔尔认为:学习数学的唯一正确方法是对知识进行“再创造”,所以,在我们学习中有必要对例题、试题进行延伸与拓展.

4 中点弦问题应用

例2已知椭圆+y2=1.

(2)求斜率为2 的平行弦的中点轨迹方程;

(3)过A(2,1)引椭圆的割线,求截得的弦的中点的轨迹方程.

分析设涉及弦两端点分别为M(x1,y1),N(x2,y2),线段MN的中点P(x,y),由上面结论3 可以知道:(1)当AP不平行坐标轴时,kl·kOP=再补充说明特殊情况即可.

解析由分析知(1)由点得kOP=1,得kMN=故所求直线方程为:y−即2x+4y−3=0.代入椭圆方程x2+2y2=2 得符合题意,2x+4y−3=0 为所求.

(2)由题意kl=2 恒成立,代入可得kOP=是定值,故知P轨迹为过原点且斜率为的线段,由解得所求轨迹方程为:x+4y=

(3)过A的直线不平行坐标轴时,将代入kl·kOP=得x2+2y2−2x−2y=0(x ̸=2,x ̸=0),当过A的直线平行x轴或y轴时,可得弦中点为(0,1)或(2,0)满足上式方程,故所求轨迹方程为:x2+2y2−2x−2y=0.

评注本题利用中点弦模型,即弦所在直线的斜率与弦中点和原点所在直线的斜率相乘的定值关系,简单快速的解决了学生平常觉得困难的问题.考生实践做题时,对于中点弦模型基本用上面结论可轻松解决,掌握了相关结论的内涵及外延可以完善知识结构和构建完整的知识网络,在考试中可以迅速找到解题的切入点与突破点.

另外,做为解答题解决椭圆中点弦问题可用点差法:利用端点在曲线上,坐标满足方程,将端点坐标分别代入椭圆方程,然后作差,构造出中点坐标和相关斜率得到定值关系再进行求解.

强化训练2(1)过点M(1,2)作直线l:y=+m与椭圆=1(a>b>0)相交于A,B两点,若M是线段AB的中点,则该椭圆的离心率是( ).

(2)已知椭圆E:=1(a >b >0)的右焦点为F(3,0),过点F的直线交椭圆E于A,B两点.若AB的中点M坐标为(1,−1),则E的方程为______.

(3)椭圆E:mx2+ny2=1 与直线l:x+y=1 相交于A,B两点,过AB中点M与坐标原点连线斜率为则=( ).

分析作为选择题或填空题,应用相应结论可快速解决问题,根据结论3 在(1)小题中,kl·kOM=且kl=kOM=2 可求得的值;在(2)小题中kl·kOM=kF M·kOM=结合F(3,0) 可得的值;(3)小题中kl·kOM=

解析(1)由分析可得所以该椭圆的离心率

(2)由已知c=3,kl·kOM=kF M·kOM=·(−1)=所以即a2=2b2.又a2=b2+c2=b2+9,所以b2=9,a2=18,即E的方程为

强化训练 3如图,已知某椭圆的焦点是F1(−4,0),F2(4,0),过 点F2并垂直于x轴的直线与椭圆的一个交点为B,且|F1B|+|F2B|=10,椭圆上不同的两点A(x1,y1),C(x2,y2)满足条件:2|F2B|=|F2A|+|F2C|.

(1)求该椭圆的方程;

(2)求弦AC中点的横坐标;

(3)设弦AC的垂直平分线的方程为y=kx+m,求m的取值范围.

研究区内土壤总体偏酸性，养分含量较为丰富，但部分地区缺乏有机质、速效钾，大部分地区微量元素缺乏。除此之外，高等级地土层厚度、灌溉保证率等立地条件、理化性状较好，基本不受限制；中等级地受部分土层厚度、灌溉保证率的影响，存在一定限制性；低等级地土层厚度、耕层质地、灌溉保证率影响较大，存在较多限制性因素。

分析利用定义或待定系数法可解决椭圆方程,利用两点距离公式可解决|F2A|,|F2C|,同时可知道弦AC的中点落在线段BB′上,对于(3)小题,设弦AC的中点为P(x0,y0),由前面可知y0=kx0+m,根据定值kOP·kAC=且kAC=可得所以kx0=则m=y0−kx0=结合y0范围可求得m范围.

解析(1)由椭圆定义及条件知,2a=|F1B|+|F2B|=10,得a=5,又c=4,所以故椭圆方程为

(2)由点B(4,yB) 在椭圆上,得|F2B|=|yB|=有因为由此得出x1+x2=8.设弦AC的中点为P(x0,y0),则x0==4.

(3)由分析可得4k=(当k=0 时也成立).由点P(4,y0) 在弦AC的垂直平分线上,得y0=4k+m,所以m=y0−4k=由点P(4,y0)在线段BB′(B′与B关于x轴对称)的内部,得所以

评注此题考查直线、椭圆等综合知识,前两问较简单,第三问巧妙地借助中垂线性质,利用已学的中点弦模型可把问题化归为关系式进行范围求解,设计新颖,综合性,灵活性强.

当涉及弦的中点问题,解答题常用“点差法”设而不求,将弦所在直线的斜率、弦的中点坐标原点连线斜率联系起来,相互转化.同时还应充分挖掘题目的隐含的代数几何关系,灵活转化,往往能取得意想不到、事半功倍的效果.选择题和填空题只要直接用上面结论可轻松解决,结论看似简单,应用却非常广泛,值得关注.

5 综合应用

例3(2020年全国I 文21 理20)已知A,B分别为椭圆=1(a >1)的左、右顶点,G为E的上顶点,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(2)证明:直线CD过定点.

分析(1)由已知可得:A(−a,0),B(a,0),G(0,1),即可求得结合已知即可求解;(2)注意到A,B两点关于原点对称,由结论1 可得

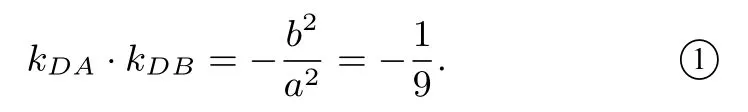
设P(6,y0),可得直线AP的斜率为:kAP=即kAC=另一方面,直线DB的斜率为kDB=可知

由①②可知,kAC·kAD=进而设直线CD方程可求解.

解析(1)依据题意作出如下图象: 由椭圆方程E:+y2=1(a >1)可得:A(−a,0),B(a,0),G(0,1),=(a,1),−−→GB=(a,−1),所以=a2−1=8,a2=9,故椭圆方程为:+y2=1.

(2)证明:设P(6,y0),由分析可知kAC·kAD=设C(x1,y1),D(x2,y2),直线CD的方程为x=ty+m,联立椭圆方程可得:整理得(t2+9)y2+2tmy+m2−9=0,则有所以

评注此题通过直线DA与DB斜率积为定值,转化为直线DA与DC斜率积为定值,应用之妙,存乎一心,找到问题本质,切中要害,迎刃而解.

美国心理学家布鲁纳认为“探索是数学的生命线”.我们可以借助一些经典例题,进行“点拨与剖析”“延伸与拓展”和“类比推理”三重途径,提高学习效率.

圆锥曲线命题灵活多变,只有通过不断的探究和发现,掌握好其包含的各种代数、几何特征,探究三种圆锥曲线相似、相异的地方,大胆类比,大胆想像,才能更好的深入学习到圆锥曲线的精髓,在双曲线与抛物线中,相似特征比比皆是,请读者认真总结,把相关结论推广到双曲线、抛物线.