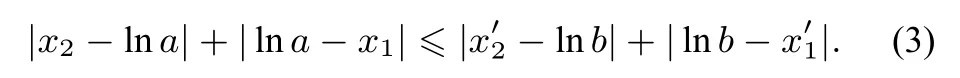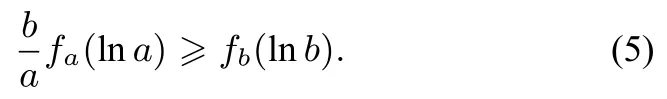多角度解透一道导数题

四川省成都市第七中学(610041) 巢中俊 周莉莉

1 题目

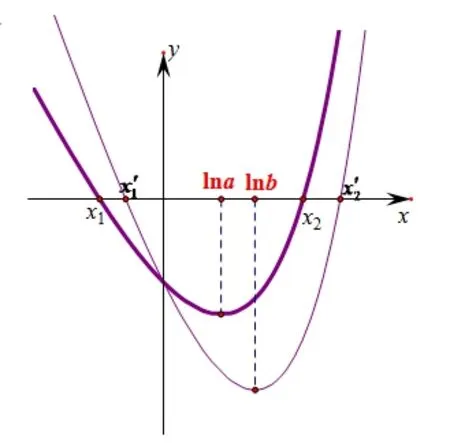
已知f(x)=ex−ax−2 有两个不同的零点x1,x2,且x1

这道题简洁优美,有一定的难度.下面将从四个不同的角度来分析求解.

2 多角度求解

角度1x1,x2是方程ex−ax−2=0 的两个不同的实数根,a易表达为x1,x2的显函数,这似乎与求解方向背道而行;逆向思维提示用a来表达x1,x2,但遗憾的是x1,x2无法用a的显式来表示.退而求其次借助隐函数工具(x1=x1(a),x2=x2(a))来求解,于是乎柳暗花明.

我们不难知a>0,x1<00.对方程ex−ax−2=0 两边关于a求导得exx′−x−ax′=0,解得即所以

把ex1=ax1+2,ex2=ax2+2 代入(1)式得注意到ex1−a=f′(x1)<0,ex2−a=f′(x2)>0,x2−x1>0.当a <2 时,当a>2 时,>0,所以x2−x1取到最小值时a=2.

角度2x1,x2是方程ex−ax−2=0 的两个不同的实数根,参变分离得a=数形结合帮助我们洞察到x2−x1的几何意义为直线y=a与y=的两交点之间的距离,于是乎船到桥头.

可以得到g(x)=的图象是两支且分别位于y轴两侧,直线y=a分别交g(x) 两支于A(x1,a),B(x2,a)把g(x)的图象的左支沿着平行移动直到与g(x)的图象的右支首次相接触,移动距离即为x2−x1的最小值.此时触点处的切线为平移后的左支与右支的公切线.所以当x2−x1取最小值时对应的A,B两点处的切线为平行直线,故g′(x1)=g′(x2).

注意到g′(x)=且ex1=ax1+2,ex2=ax2+2,故即因为x1̸=x2,所以a=2,所以x2−x1取到最小值时a=2.

角度3x1,x2是方程ex−ax−2=0 的两个不同的实数根,我们表达为

(2)式中两式相减得a(x2−x1)=ex2−ex1=即结合ex1−ax1−2=0我们把x2−x1的最小值转化化归为单变量函数的最值问题,于是乎别有洞天.

令x2−x1=t,则记g(t)=,t >0,二次求导得g(t) 关于t单调递减.故x2−x1=t取最小值转化为取最大值.结合ex1−ax1−2=0,求的最大值的处理方法较多:例如解出a=代入得求导分析得ex1−2x1−2=0时,取最大值,此时a==2;再例如记m=则x1=lnam,于是am−alnam−2=0,故m−lnm=lna+注意到f′(x1)=ex1−a <0,a >0,故m ∈(0,1).易知m−lnm关于m单调递减,m=取最大值再次转化为lna+取最小值.不难论证lna+在a=2 时取到最小值.所以x2−x1取到最小值时a=2.

角度4x1,x2是方程ex−ax−2=0 的两个不同的实数根,a的变化引起x1,x2的变化,传导引起x2−x1的变化.考虑x2−x1取最小值的实数a,对比不同于a的实数b产生的x′2−x′1,分析出a满足的条件关系,于是乎返朴归真.记fa(x)=f(x)=ex−ax−2.

不难得到a >0 且fa(x)的最小值为fa(lna)=a−alna−2<0.考虑使得x2−x1取最小值的实数a,则x10,b ̸=a,设fb(x)=ex−bx−2 的两个不同的零点为x′1,x′2,则x′1

图1

由x2−x1的最小性知x2−x1≤x′2−x′1,即(x2−lna)+(lna−x1)≤(x′2−lnb)+(lnb−x′1),也即

由(3)式知存在i ∈{1,2}使得

记f′a(x)=f′(x)=ex−a,对任意的t ∈R,计算得f′b(lnb+t)=从而即fb(lnb+t)−fb(lnb)=t)−fa(lna)].令xi−lna=t,由(4)式可得fb(lnb+t)≤fb(x′i)=0.注意到fa(lna+t)=fa(xi)=0,从而

令λ=于是(5)式为λ(a−alna−2)≥λa−λalnλa−2,化简得a(λlnλ)≥2(λ−1).注意到lnλ≤λ−1,所以于是λlnλ≥λ−1.若λ>1,则故a≥2;若0<λ<1,则故a≤2.于是a=2,所以x2−x1取到最小值时a=2.

通过这四个不同的角度解穿[1]、解透[2][3]这道导数题,我们可以清晰地认知到这道导数题的内在本质.