以小见大探细节 深入思维寻方法
——以一道教材应用题为例
广东省广州市二中苏元实验学校(510000) 张亚茹
1 原题呈现
从甲地到乙地有一段上坡与一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
本题源自人教版教材七年级下册第102 页第6 题,考查的基本知识为:实际问题与二元一次方程组——行程问题,考查的基本能力为:能够根据题意,设立恰当的未知数,列出方程或方程组;能够选择恰当的方法,求出方程组的解,解决实际问题.用二元一次方程组解决的应用题类型很多,其中的行程问题、工程问题、分配问题等,都是近几年考试的热点问题.
2 试题分析
在这道行程问题的应用题中,涉及的路程有:从甲地到乙地的路程、从乙地到甲地的路程、上坡路、平路、下坡路.学生审题时,结合生活实际,不难得出这几段路程之间的关系:从甲地到乙地的路程=从乙地到甲地的路程,从甲地到乙地的路程=上坡路+平路,从乙地到甲地的路程=平路+下坡路,还应该注意的是,平路的长度不变,上坡路的的长度=下坡路的长度.
在本题中,涉及的速度有:上坡时的速度是每小时3km,平路每小时走4km,下坡每小时走5km,在不同的路段,因为速度不同,所用的时间也就不同.涉及的时间有:从甲地到乙地的时间是54min,从乙地到甲地的时间是42min,时间的单位是以“min”也就是“分钟”为单位,速度的单位是“km/h”也就是“千米/小时”,所以,在时间的单位上,存在着巨大的陷阱,审题时没能引起对“时间单位不统一”的关注的同学,本题做错的风险大大提升了.
在本题中,路程、速度、时间,三者之间的关系为:路程=速度×时间,速度=路程÷时间,时间=路程÷速度,用哪个量建立等量关系好呢? 选取的等量关系不同,决定设立的未知数以及建立的方程都会有所不同.
结合以上对试题的分析,如果以时间为等量关系,则比较容易得出:从甲地到乙地的时间=上坡路所用的时间+平路所用的时间,从乙地到甲地所用的时间=平路所用的时间+下坡路所用的时间.关于时间的统一,可以将分钟转化为小时,也可以将“千米/小时”转化为“千米/分钟”,尽管后者不常用.
3 解法探究
解法1设坡路长为xkm,平路长为ykm.54 min依题意列方程组得:或者列成均可,解得
如果以路程相等建立等量关系,则有:从甲地到乙地的路程=从乙地到甲地的路程.因为在平路所用的时间是相同的,而平路所用的时间又与上坡所用的时间和下坡所用的时间都有联系,所以可以设平路的时间为未知数,利用路程相等建立方程,此种解法仍需转化时间单位.
解法2设平路所用的时间为th,则上坡所用的时间为下坡所用的时间为根据路程相等,列一元一次方程得:解得t=0.4,计算+4t=2.7−1.2+1.6=3.1km.
从解法2 中,我们可以获得新的灵感,既然从甲地到乙地的平路路程=从乙地到甲地的平路路程,平路的路程与速度都相等,则所用的时间也是相等的,那么54 min-42 min=12 min=就是这段坡路因为上坡和下坡的速度不同产生的时间差,由此,我们可以得到更为简洁的方法.
解法3解:设坡路长为xkm,依题意得:解得:x=1.5,再计算=1.5+1.6=3.1km.这种解法在计算上非常简便,但是在思维能力方面的要求上,明显比解法1 和解法2 的要求更高一些.
在思考的过程中,也可以同时抓住“时间”和“路程”两个量来建立等量关系,此时可以列出如下的三元一次方程组.
解法4设上坡路用xh,平路用yh,下坡路用zh,依题意列方程组得: 54 min=0.9 h,42 min=0.7 h.解得:再计算3×0.5+4×0.4=3.1km.这种解法也很有自己的优势,在列方程和求解方程上都非常自然和简洁.
4 学生思维障碍分析
本题在七年级第二学期期末检测中作为第20 题考查过,该题满分6 分,全级得分平均为为3.27 分,从阅卷情况看,答题情况很不理想,零分的人数占40%左右,特别值得关注.笔者通过对全级学生的答题情况进行分析,发现学生的解题思维障碍主要体现在以下几个方面.
4.1 审题不仔细,忽略细节
学生在审题时,不够细心,没有发现时间的单位不统一,得零分的学生,有一大部分比例是因为这个细节出错.典型错误如下:
解设坡路长为xkm,平路长为ykm,依题意列方程组得解得:然后计算得x+y=90+96=186km.
更为关键的是,学生没有结合实际检验一下,这个结果是否可能,也就是说,从结果来看,从甲地到乙地共186km,步行竟然只需54min,这完全不符合生活实际,如果有这种检验的意识,也会发现自己列的方程是有问题的.
4.2 转化能力弱,不能准确找出等量关系
部分成绩比较弱的学生,读不懂题意,或者直接用错路程、速度、时间三者之间的关系,典型错误如下:
解设坡路长为xkm,平路长为ykm,依题意列方程组得或者方程中出现了“路程×速度=时间”这样的错误,平时的教学中,也常常发现学生对“顺水逆水问题”、“相遇问题”、“追及问题”等行程问题的理解和掌握,都还有很大的提升空间.
4.3 计算能力不过关
除了单位转化这个难点之外,解方程组成为了另一个难点,计算能力不过关,或导致计算过程中的各种失误.
错误1少数学生列出方程组之后,不会利用“加减消元法”进行消元,或者不会去分母,将方程组化为整数系数的方程组,出现了混乱的计算.也有学生将方程成功的化简为后,计算的结果没有约分,得到了然后在计算时,数据比较大,导致了计算的失误.个别学生计算对了一个结果,代入求另一个结果时出现错误,还有学生写反了分子分母,得到等.
错误2成功的转化了3km/h=却将方程组错误的列为:非常可惜.
错误3个别学生把数据写反了,方程组列成了虽然只是很少数的学生,但是也提醒我们,一定要看清楚数据,写错一个数据就全盘皆输了.
错误4时间单位转化错误,将54 min=0.54 h,42 min=0.42 h,方程组错误的列成了分钟与小时的转化,是60 进制,学生错误的按百分制进行了转化.
5 反思与启示
通过对学生答题的思维障碍分析,我们发现,教师在教授应用题解题时,可以注重以下方面的一些改进.
(1)通过一些典型的例子,教学生如何审好题,在读条件、分析条件、利用条件的同时,一定要特别留意细节,比如本题的单位转化,比如人教版教材七年级下册第126 页第7题,也同样存在“元”与“万元”的单位转化.
(2)在解应用题时,列图表、画示意图等都有利于分解题目难度,帮助学生快速、准确的找出等量关系.比如,此题中,涉及的路程、速度、时间等,在审题时,可以列出下列的表格帮助分析:
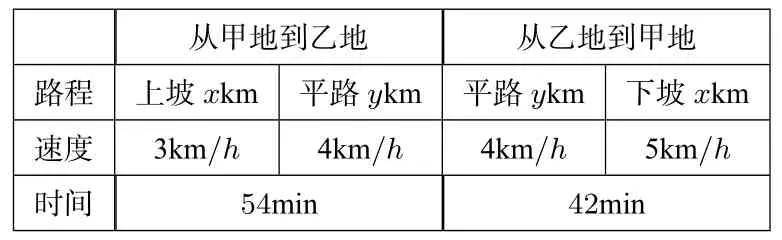
从甲地到乙地从乙地到甲地路程上坡xkm 平路ykm 平路ykm 下坡xkm速度3km/h 4km/h 4km/h 5km/h时间54min 42min
画出这样的示意图帮助分析:
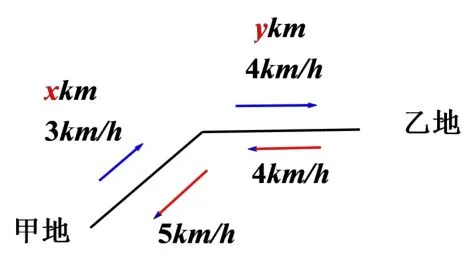
(3)在应用题的“审”、“设”、“列”、“解”、“检验”、“答”环节中,教学中要注意各种应用题模型在以上环节中的技巧,尽量减少计算方面的丢分,并强调在问题解决之后的检验.
(4)教学中不能脱离教材,用好教材中的例题、课后题,深挖典型题目的作用,引导学生发散思维,深入学习和探讨多种方法解决问题,培养和提升学生分析问题、解决问题的能力.

