例谈回归椭圆定义解题,提升学生运算素养

江苏省盱眙中学(211700) 周志国

认识事物需要透过现象看本质,解题更是如此,只要理清问题本质,回归本源,解题便是水到渠成之事.椭圆是高中数学中非常重要的内容之一,也是难点,如何处理与椭圆有关的问题? 首先要深刻认识椭圆的各种定义,并学会串联,关注与其它内容之间的联系.下面通过例析如何回归椭圆定义解题,以飨读者.

1 椭圆第一定义是本,解题不忘本

1.1 利用椭圆第一定义,从几何视角认知并化简方程

例1在实数范围内解方程

分析常规解法是移项,平方,将两个根号退化成仅有一个根号,再移项,平方,将无理式化成有理式,并解方程,但其运算过程繁杂,难以在短时间内完成.倘若联想到椭圆第一定义,将方程配方后令1=y2,得则点M(x,y)的轨迹是以F1(−1,0),F2(1,0)为焦点,长轴长为4 的椭圆,进而原方程的解等价于已知椭圆上点的纵坐标,求该点的横坐标.

解析由原方程可得所以解得

评析解题过程是思维过程的体现,解较复杂的代数方程时,方程化简运算过程,更加凸显出多想一点,少算一些.从不同的认知角度观察,关注方程整体结构特征,发散思维,用不同视角等价转化条件,从数与形两个方面相互转化,寻找实切的运算对象,从解题中不断提升自身的思维能力.

1.2 巧用椭圆第一定义,搭起均值不等式桥梁

例2(2004年高考数学全国卷III)设椭圆=1 的两个焦点分别是F1(−c,0),F2(c,0)(c >0),且椭圆上存在点P,使得直线PF1与直线PF2垂直,求m的取值范围.

分析根据焦点三角形ΔF1PF2为直角三角形,得到三边之间的平方关系:|PF1|2+|PF2|2=|F1F2|2,再结合点P在椭圆上,应满足椭圆第一定义,再通过均值不等式建立关于m的不等式,进而求出m的取值范围.

解析由题意知m >0,a=且满足

②2−①得,|PF1|·|PF2|=2a2−2c2=2b2,又所以2b2≤a2,即2≤m+1,所以m≥1.

评析椭圆第一定义中“|PF1|+|PF2|=2a”恰与均值不等式“|PF1|·|PF2|≤”一端直接有关,因此,在处理与焦点三角形ΔF1PF2中的PF1,PF2有关的最值范围问题时,可以尝试利用椭圆第一定义,将条件等价表示,搭起与均值不等式的桥梁.

1.3 活用椭圆第一定义,变“折线”为“直线”求最值

例3(1999年全国数学联赛) 已知椭圆内有一点P(1,−1),F为椭圆右焦点,M是椭圆上动点,求|MP|+|MF|的最小值.

分析联想到求一条直线上一个动点到两个定点的距离之和的最值时,两点需要分布在直线的两侧,而两点如果在直线的同一侧时,距离只差的绝对值应该有最大值.类比,尝试利用椭圆定义把|MP|+|MF|转化成|MP|+2a−|MF′|,即4+|MP|−|MF′|,再根据平面几何知识,两边之和大于第三边,转化成两个定点之间的距离问题.

解析设椭圆的左焦点为F′,所以|MP|+|MF|=|MP|+2a−|MF′|=4+|MP|−|MF′|≥4−|PF′|=当且仅当M为线段F′P的延长线与椭圆交点时取等号.所以|MP|+|MF|的最小值为

评析从本题转化中看出,在使用椭圆第二定义时,不仅要把点点距离转化为点线距离,而且还调整了中|BF|前面的系数,让|BF|前面的系数和|AB|前面的系数一致,真可谓一举两得.因而,涉及椭圆中有关折线的最值问题时,可以通过椭圆的两种定义,设法将折线拉直,转化为两点间的距离或者点到直线的距离问题,原问题便迎刃而解.

1.4 逆用椭圆第一定义,求轨迹

例4(2002年春季高考) 已知椭圆的焦点是F1,F2,P是椭圆上一个动点,如果延长F1P到Q,使得|PQ|=|PF2|,那么动点Q的轨迹是( )

A.圆 B.椭圆

C.双曲线一支 D.抛物线

分析将延长F1P到Q,使得|PQ|=|PF2|,相当于把PF2绕着点P旋转使得和F1P在一条直线上,满足QF1为定值,Q点轨迹是圆.

解析因为|PQ|=|PF2|,所以|QF1|=|PQ|+|PF1|=|PF2|+|PF1|,由椭圆第一定义得|PF1|+|PF2|=2a,故|QF1|=2a,即Q点轨迹是以F1为圆心,以2a为半径的圆,选A.

评析在2021年苏教版教材选择性必修一中,通过折纸实验操作,探究得知椭圆可以由圆折叠,折痕交点的轨迹生成椭圆;反之,由椭圆上的点通过旋转变换(或者对称变换)也可以还原成圆,两者可以互相生成,在解题过程中要关注它们之间内在联系,借助图形,架起两者之间沟通的桥梁.

1.5 调用椭圆第一定义,解焦点三角形

例5已知点P是椭圆(a>b>0)上的一点,F1,F2是两个焦点,且∠F1PF2=α,求ΔF1PF2的面积S.

分析联系已知条件∠F1PF2=α和所求ΔF1PF2的面积,根据点P是椭圆(a >b >0)上的一点,用余弦定理和椭圆定义即可求出|PF1||PF2|的值,再利用SΔP F1F2=|PF1||PF2|sinα求出ΔF1PF2的面积S.

解析因为点P是椭圆(a >b >0) 上的一点,F1,F2是两个焦点,所以|PF1|+|PF2|=2a,在ΔPF1F2中,由余弦定理,得

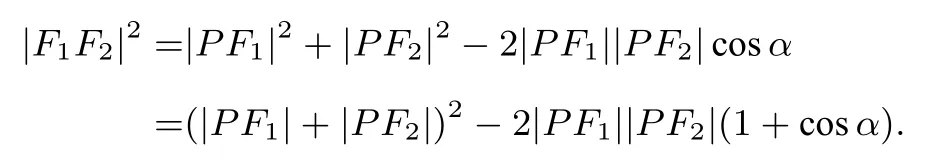
所以|PF1||PF2|=故SΔP F1F2=

评析椭圆的第一定义涉及焦点三角形的两条边,因而在涉及焦点三角形问题时,要心怀椭圆定义,从椭圆定义出发,用定义刻画椭圆上点的几何意义,并联合三角形中的正弦定理或余弦定理,再从方程组的角度认知条件,解决问题便水到渠成.

例6已知P是椭圆C:(a>b>0)上一点,F1,F2是椭圆的左、右焦点,若∠PF1F2=α,∠PF2F1=β,求椭圆C的离心率(用α,β表示).

分析由焦点三角形ΔPF1F2中的两个角∠PF1F2=α,∠PF2F1=β,利用正弦定理,得到等式

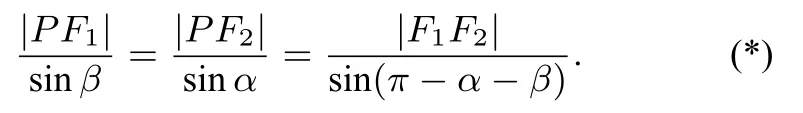
解析设椭圆C的离心率为e,在ΔPF1F2中,由正弦定理有用合比定理,得到即所以

评析椭圆的焦点三角形中含有了离心率所需的两个量a,c,在处理此类问题中,利用解三角形知识,设法寻找焦点三角形中的边角等量关系,打通条件和设问之间的通道.

1.6 妙用椭圆第一定义,搭桥椭圆与圆

例7(2019年高考数学江苏卷) 如图,在平面直角坐标系xOy中,椭圆C:=1(a >b >0) 的焦点F1(−1,0),F2(1,0).过F2作x轴的垂线l,在x轴的上方,l与圆F2: (x−1)2+y2=4a2交于点A,与椭圆C交于点D.连结AF1并延长交圆F2于点B,连结BF2交椭圆C于点E,连结DF1.已知

(1)求椭圆C的标准方程;

(2)求点E的坐标.

分析根据条件“圆F2: (x−1)2+y2=4a2”可得圆F2的圆心F2(1,0)恰好为椭圆C:=1(a>b>0)的右焦点,半径长2a,也恰好等于椭圆C的长轴长,结合椭圆的定义,可得EF1=EB,即从而∠BF1E=∠B,再结合圆的特征,得到∠A=∠B,从而EF1//F2A,EF1⊥x轴,最后转化成求直线x=−1 与椭圆C的交点的坐标.

例7 图1

例7 图2

解析(1)略;(2)由(1)知,椭圆C:=1.如图所示,联结EF1.因为BF2=2a,EF1+EF2=2a,活用定义,在结合圆的条件,所以EF1=EB,从而∠BF1E=∠B.因为F2A=F2B,所以∠A=∠B,所以∠A=∠BF1E,从而EF1//F2A.因为AF2⊥x轴,所以EF1⊥x轴.因为F1(−1,0),由得又因为E是线段BF2与椭圆的交点,所以y=因此

评析本题如按照构图过程,逐步求解,求解过程复杂,中间衔接的过渡点,不必要求解的也一并求解了,且加大了运算的复杂程度和难度.利用椭圆的第一定义,从几何的角度分析,直接得到问题的解决.

2 椭圆第二定义是魂,解题不能丢魂

2.1 关注结构,从“形”到“数”

例8已知x,y ∈R,且满足试判断点M的轨迹是怎样的曲线.

分析从“形”的角度上认知,等式左边可看作两点M(x,y)和(2,0)之间的距离,进一步观察,发现右边与点M到直线x+y−2=0 的距离有关,按此路径,结合椭圆第二定义,便得到了所求点M的轨迹是椭圆.

解析由原方程可得这式子表明点M到点(2,0)的距离和点M到直线x+y−2=0 的距离之比为

评析若将原方程平方,化简不易,即使化简完成,根据化简后的结果判断其轨迹特征也是比较困难的.我们面对这类问题,倘若我们有着“横看成岭侧成峰,远近高低各不同”意识,变换角度,挖掘等式中所隐藏的几何特征,善于向着目标变形转化,寻找其形的特征,便不难突破难点,问题便顺利解决.

2.2 关注差异,求同存异

例9(1999年全国数学联赛)给定A(−2,2),已知B是椭圆=1 上动点,F是左焦点,当取最小值时,求B点坐标.

分析此题如果按一般求最值的方法先建立目标函数,再求最值,因含有两个根式的和,代入消元不易,难以求解,但如果我们关注到所求的问题涉及椭圆上的点到焦点的距离,借助椭圆定义,从“形”上,结合平面几何知识,合理化归转化.

解析(1)因为所以点A在椭圆内部,由椭圆第二定义可得:B到椭圆左准线l的距离所以结合平面几何知识,可知,当AB⊥l时,|AB|+d最小,此时易求B点坐标为

评析从本题转化中看出,在使用椭圆第二定义时,不仅仅把点点距离转化为点线距离,而且还调整了中|BF|前面的系数,让两其系数和|AB|前系数一致,可谓一举两得.因而,涉及椭圆中有关折线的最值问题,通过椭圆的第二定义,设法将其拉直,实现转化,顺利求解.

3 椭圆第三定义是神,解题需神来助

例10(2011年高考数学江苏卷) 如图,在平面直角坐标系xOy中,M,N分别是椭圆的顶点,过坐标原点的直线交椭圆于P,A两点,其中点P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B.设直线PA的斜率为k.

图(例10)

(1)当直线PA平分线段MN,求k的值;

(2)当k=2 时,求点P到直线AB的距离d;

(3)对任意k >0,求证:PA⊥PB.

分析本题设问PA⊥PB,只要证明出kP A·kP B=−1,而结合椭圆第三定义得知,kBA·kP B=因而只要能够证明kBA=即可.

解析(1)(2)略:(3)设B(x,y)(|x|̸=x0),P(x0,y0)(x0>0,y0>0),则A(−x0,−y0)(x0>0,y0>0),所以作差,得则kBA·kBP=而kBA=kAC=所以kP A·kP B=−1,所以PA⊥PB.

评析在处理与椭圆有关的多条直线斜率相互关系的问题中,不要忘记椭圆有一种定义与直线斜率也直接相关,即:动点P和两定点构成直线的斜率乘积为定值µ(λ<0 且λ ̸=−1),则动点P的轨迹是椭圆,在解决问题时,要善于寻找它们之间关联直线,搭起解决问题的桥梁,提升我们的运算求解能力和推理论证能力.

4 借力变换,“椭圆”还“圆”

例11(2019年南通二模)如图,在平面直角坐标系xOy中,已知椭圆C1:椭圆=1(a>b>0),C2与C1的长轴长之比为离心率相同.

(1)求椭圆C2的标准方程;

(2)设点P为椭圆C2上一点.

①射线PO与椭圆C1依次交于点A,B,求证:为定值;

②过点P作两条斜率分别为k1,k2的直线l1,l2,且直线l1,l2与椭圆C1均有且只有一个公共点,求证:k1·k2为定值.

分析根据条件可知,椭圆C1:椭圆离心率相同,对于两曲线和直线都实施变换:所有的点横坐标变为原来的一半(纵坐标不变),便可以把两曲线都变换成圆,问题转化成变换后的直线与圆的相关问题.

例11 图1

例11 图2

解析(1)过程略,椭圆C2的标准方程为

(2)①略

评析我们熟知,在处理直线与圆的位置关系问题时,可以通过联立直线和圆的方程,转化成二次方程来求解,还可以根据“形”的特征,用几何意义来转化求解.而椭圆是由圆通过线性变换(伸压变换)而来的,变换过程中仍然保证位置关系不变性.因而,在处理椭圆问题中,调整了运算对象,还“圆”处理,紧扣圆的特殊性,借助于圆的几何意义,以形助数,优化了算理,简化了运算过程,提高了运算正确率,进而提升了数学运算素养.

总结数学中的定义是问题的起源,本文通过对几道与椭圆有关的例子分析、解析与评析,点明了数学中的定义在解题过程中不可忽视,在解题过程中要能抓住问题核心,要善于从不同的角度理解认识问题,抓住问题本质,问题从哪里来回到哪里去,不能舍近求远,本木倒置,多思少算,思与想贯穿数学解题的始终,用数学的眼光解题,提升我们的思维能力和运算素养.