概率统计教学中思维品质培养例谈

李立明

（吉林大学数学学院公共数学教学与研究中心，吉林长春 130012）

概率统计是大学数学教育的一门重要课程，与其他研究确定性现象的数学学科不同，概率统计研究的是随机现象的内在统计规律性，是解决随机性问题的强有力工具[1]。在概率统计的教学中一定要重视培养学生的思维品质，以及培养学生用概率统计的思维方式解决各种随机问题的能力。通过养成良好的思维习惯，来提升内在的数学素养，实现大学数学教育的价值。概率统计教学中应培养学生的哪些思维品质呢?下面从四个方面结合教学实例进行探讨。

1 “比较与联想”的思维品质

概率统计教学中的很多内容，表面上看似毫无关联，实际却是可以沟通互化的。在讲授比较抽象晦涩的概念时，教师应遵循学生的认知规律，从学生比较熟悉、易于理解的旧的概念出发，挖掘新旧知识之间的联系，找到二者之间的契合点，然后启发和引导学生深入思考，通过区分比较和广泛联想，由旧概念顺其自然地延伸和推广出新的概念。学生亲历了概念的形成过程，不仅加深了对新概念的理解，而且主动思考的过程，会激发学生探究的兴趣和探索的精神，既锻炼了思维品质，也实现了思维的延伸和推广。

1.1 在“数学期望”的概念教学中，培养学生“比较与联想”的思维品质

“离散型”和“连续型”随机变量是概率论中最重要的随机变量类型[2]。“离散型”随机变量的数学期望，直观、易懂，而“连续型”随机变量的数学期望，则较为抽象，不易被接受。在教学实施过程中，教师要启发和引导学生将这两种随机变量的特征加以比较，分析它们的不同点和相同点，找到联系二者的桥梁，将这两种随机变量沟通互化，先将连续取值的随机变量X“离散化”，求出它的数学期望，再将离散取值的随机变量X“连续化”，就可以轻松地把数学期望的概念由“离散型”随机变量延伸和推广到“连续型”随机变量[3]。

设X 为密度函数为f(x)的连续型随机变量，取很密集的分点x0＜x1＜…＜xn，则X 在区间△xi=(xi, xi+1)内取值的概率为当△xi充分小时，就有P(X∈△xi)≈f(xi)△xi。此时连续型随机变量X 就被“离散化”，它可以近似地看成是具有概率分布的离散型随机变量，从而数学期望为

最后只需将离散取值的随机变量X“连续化”就行了。事实上，让分点无限变密就可以实现X“连续化”，同时对和式取极限便得到，这就是连续型随机变量X 的数学期望的定义表达式。

1.2 在“几何概型”的概念教学中，培养学生“比较与联想”的思维品质

“古典概型”与“几何概型”是概率统计教学中的两种重要的概率模型。“古典概型”的定义，具体、直观，其中n(A)表示随机事件A 中的样本点个数，n(Ω)表示样本空间Ω中的样本点个数。在讲授“几何概型”的定义时，教师启发学生将“几何概型”与“古典概型”进行类比，牢牢抓住“样本点等可能出现”这个本质属性，把样本点的个数由有限推广到无限，就可以顺其自然地得到“几何概型”的定义，其中L(A)表示随机事件A 对应的区域的测度，L(Ω)表示样本空间Ω对应的区域的测度。

在概率统计的课堂教学中类似的实例还有很多，比如，两个随机事件的独立性通过比较可以联想到2个随机变量的独立性；一维随机变量的均匀分布通过类比可以推测二维随机变量的均匀分布；连续型随机变量X 的数学期望通过类比可以得到它的函数g(X)的数学期望，等等。

2 随机性思维品质

人类生活在一个充斥着随机现象的世界，各种不确定因素随处可见。然而随机现象并非杂乱无章，当同类随机现象大量涌现时，就会呈现出一定的数量变化规律。在概率统计的教学中，教师应紧密联系生活中的随机事件，引导学生改变传统的确定性思维方式，学会运用随机性思维来分析和处理问题，激发学生的随机性数学意识，培养他们的随机性思维品质。

2.1 运用案例教学，培养学生的随机性思维品质

例题1：假设每位学生的生日在一年365 天中的任何一天是等可能的，即都等于1/365，求64 位学生中至少有2 人生日相同的概率。

解：试验的样本点总数为36564，事件“64 位学生生日各不相同”包含的样本点数为365 364…(365-64+1)，于是64 位学生生日各不相同的概率为，故64 位学生中至少有2人生日相同的概率为

例题1 完成后，让全班64 个学生依次有序地写出自己的生日，然后教师略做统计，很快发现确实有两个学生生日完全相同。随着结果的公布，许多学生都感到很惊奇，不由得感慨概率统计的奇妙。通过这个有趣的随机性问题，既激发了学生运用随机性思维的兴趣，也增强了学生用随机性思维解决实际问题的能力。

2.2 利用MATLAB 数学软件进行实验教学，培养学生的随机性思维品质

“列维—林德伯格（Levy-Lindberg）定理”，也称“独立同分布的中心极限定理”，是概率统计教学内容中的一个重要定理[4]。该定理表明，相互独立同分布、具有数学期望和方差的随机变量序列之和，其标准化变量以标准正态分布为极限分布。

例题2：利用MATLAB 数学软件实现中心极限定理的直观演示。

（1）产生n 个服从均匀分布U(0,1)的随机数，取n=50，计算n 个随机数的和y 以及。（2）将步骤（1）重复m=1000 次，用m 组的数据作频率直方图[5]。

解编程如下：

输出结果，如图1所示。由图形可以直观看出，当n 比较大时，n 个独立且都服从U(0,1)分布的随机变量之和近似服从正态分布。

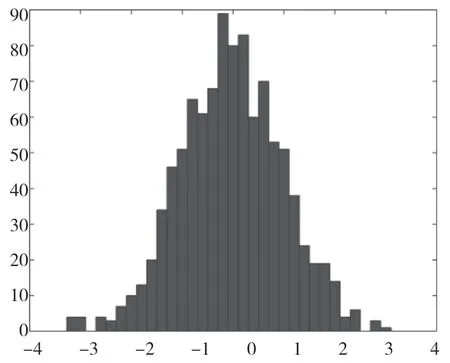
图1 输出结果

利用MATLAB 数学软件进行实验教学，让概率统计的知识具体化、形象化，使学生对概率统计的思想内涵有了更直观、明晰的领悟，在实际操作过程中，既提高了学生的应用能力，也锻炼了他们的思维品质。

3 多向的发散思维品质

聚合思维和发散思维是两种不同的思维模式。聚合思维是单一方向的思维模式；发散思维则是无规律、无定式的多方向的思维模式。聚合思维是发散思维的基础，发散思维是聚合思维的升华与发展。在概率统计的教学中，教师引导学生突破思维定式，从聚合思维方式上升到发散思维方式，就可以通过拓宽学生思维的广度、深度，增加学生思维的灵活性，达到提升思维品质、提高数学素养的目的。

概率统计教学内容中包含着各种各样的随机问题，其求解方法灵活多样，尤其是关于古典概率的计算问题，往往一题多解，一题多变，从不同的思考角度和途径出发，有着不同的解题方法。发散性思维就是要打破常规，从与众不同、别出心裁的角度出发来解决问题，往往会获得很好的效果，同时也提高了创新能力。

例题3：有5 张签，其中2 张签写着“有”字，3 张签不写字，5 人依次抽取，求第k（1≤k≤5）个人抽到写着“有”字的签的概率。

解法1：用全概率公式求解。设Ak表示求第k(1≤k≤5)个人抽到写着“有”字的签的概率。则

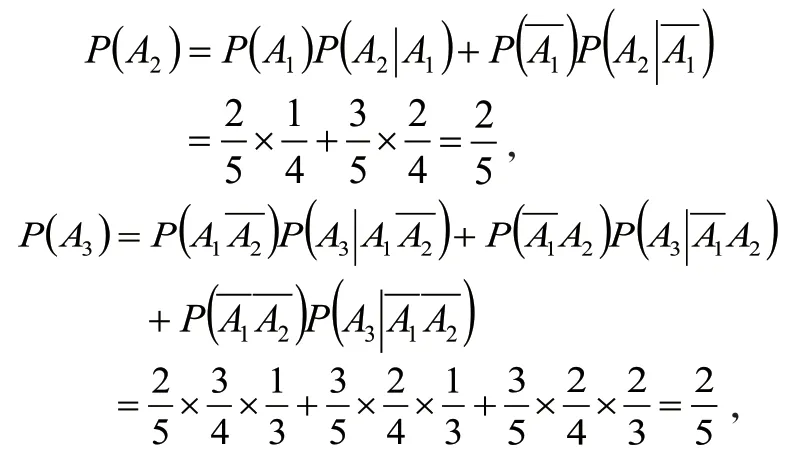
解法2：用排列的方法求解。把5 张签编号，将它们看作是彼此不同的签。把抽出的5 张签依次排列在5 个位置上，则排列法总数为5!。又因为第k 个人抽到写着“有”字的签有2 种取法，而其余的4 张签排列法为4!，因此所求概率为：

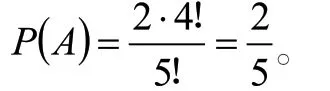
解法3：用组合的方法求解。把2 张写着“有”字的签看作是没有差别的，把3 张无字签也看作是没有差别的。把抽出的5 张签依次排列在5 个位置上，写着“有”字的签的位置有C25种放法，而其余位置必然放的是无字签，放法总数为C25。又因为第k 个人抽到了“有”字签，所以第k 个位置必须放“有”字签，另一个“有”字签在其余4 个位置上任取一个位置，因此所求概率为：

解法4：只考虑第k 次抽签。5 张签中的任何一张都有可能在第k 次被抽到，所以样本点总数为5，而抽到“有”字签只有两种可能，因此所求概率为：

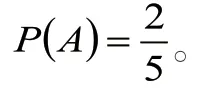
由例题3 可见，解法1 化整为零计算量较大。解法2、3、4 虽然都使用古典概率的计算方法，但随着样本空间选取的不同，解题的繁杂程度也不同。如果样本空间选取得好，那么解题会更加简便。事实上，解法4 的样本空间是最小的，它抓住了随机事件的本质特点，不考虑无关因素，化繁为简，标新立异，解法很奇妙，运算量最小。

4 逆向思维品质

逆向思维是多向的发散思维中比较重要的一个方面，在概率统计的教学中，培养学生的逆向思维品质，通过正反两方面思考问题，能够使学生的思维方式更加灵活多变，分析和解决问题的方法更加新颖和独特，有利于学生透过现象看到事物的本质，对所学的知识更好地融会贯通，而不是仅仅停留在表面上。

4.1 在典型例题的讲解过程中，培养学生的逆向思维品质

例题4：设A、B、C是同一个试验E的三个随机事件，化简（A∪B）（B∪C）[6]。

解法1：根据事件运算的分配律，有：

(A∪B)(B∪C)=[(A∪B)B][(A∪B)C]

=[(AB)∪B][(AC)∪(BC)]

=B∪(AC)∪(BC)

=B∪(AC)。

解法2：反用事件运算的分配律，直接有：

(A∪B)(B∪C)=B∪(AC) 。

由例题4 可见，正向思维的解法1 按部就班、循序渐进；逆向思维的解法2 简洁明了，一步到位，事半功倍。通过正向、逆向两种不同的思维方式，让学生对事件运算的分配律运用得更加熟练，对事件的关系理解得更加透彻。

例题5：在1，2，3，…，9 这9 个数中可重复地任取n（≥2）个数，设A 表示事件“取出的n 个数的乘积能被10 整除”，求A 的概率P(A)。

分析：直接去求事件A 的概率，要考虑的情形非常复杂，会相当麻烦。如果另辟蹊径，利用逆向思维求出A 的逆事件的概率P()，再利用概率的性质P(A)=1-P()，计算P(A)就会简单得多（注：例题1 也是用同样的思路求解的）。

4.2 在重要的统计方法教学中，培养学生的逆向思维品质

概率统计教学内容中的假设检验，是一种基本的统计推断方法。假设检验的思想方法别具一格，是基于“实际推断原理”的反证法的思想。

假设检验的过程如下：首先提出原假设H0及它的对立假设H1，在假定H0正确的条件下，构造小概率事件，接下来依据样本观测值看小概率事件发生与否，来做出决策。若小概率事件发生了，意味着不合乎情理的情况出现了，就拒绝原假设H0，接受它的对立假设H1；若小概率事件没有发生，意味着没有不合乎情理的情况出现，就接受原假设H0。

假设检验的思想方法，不仅是一种概率性质下的反证法，同时也是一种非常重要的逆向思维。

5 结语

总之，在概率统计的课堂教学中，注重培养学生“比较与联想”的思维品质、随机性思维品质、多向的发散思维品质、逆向思维品质，让学生的思维真正“活”起来，既提高了学生分析和处理随机问题的能力，提高了创新能力，也使学生获得“受用终身”的东西，最终实现学生的全面发展。