异丙醇-二氯甲烷缔合行为的实验与理论研究

黄荣谊，齐 轩，王丹丹

（安庆师范大学 化学化工学院，安徽 安庆 246133）

分子间缔合行为的复杂性及其在材料科学、生物化学、超分子化学等众多领域的潜在应用一直备受关注[1-2]。尤其是，对基于氢键作用的分子间缔合行为在实验和理论方面已进行了广泛研究[3-6]。众所周知，物质的许多物理化学性质和热力学过程均受到氢键作用的影响[7-8]，因此含氢键物质体系的分子间缔合行为引起了人们的兴趣。其中，醇是一类重要的化工原料，其羟基基团既是氢受体也是氢供体，可以与有机分子和水通过氢键作用形成交叉缔合体，也可以经自缔合作用形成氢键框架。目前，在含醇混合物的结构和性质方面已开展了较多的实验和理论工作[9-13]。然而，由于存在许多影响因素，如分子间缔合程度、分子间堆积方式、混合物组成等，分子间缔合行为的本质探讨仍是一个具有挑战性的科学问题。基于上述考虑和我们前期对分子间缔合行为的研究[14-17]，该研究通过实验和理论方法探讨了异丙醇与二氯甲烷混合物的分子间缔合行为和介电行为。

1 实验和计算部分

试剂与仪器：IPA和DCM购于国药集团化学试剂有限公司，分析纯，质量分数均大于99.5%；分析设备有瑞士Mettler-Teledo DE40型数字密度计（测量精度为±0.000 1 g·cm-3）、上海FA2204B型电子天平（测量精度为±0.000 1 g）、美国Nicolet iS50傅里叶红外光谱仪（光谱分辨率为4 cm-1）和德国Novocontrol宽频介电阻抗谱仪。

实验过程：采用称量法配制IPA和DCM混合物。采用Mettler-eledo DE40型数字密度计测定IPA、DCM及其混合物的密度。采用Nicolet iS50红外光谱仪进行样品红外光谱测试。采用Concept 41介电阻抗谱仪测定该二元混合物在摩尔分数为0.25和0.85时的介电常数和介电损耗。

计算方法：运用Gaussian 09 D01程序包[18]和DFT/M06-2x-D3方法，在6-311++G(d,p)基组下对异丙醇和二氯甲烷及其形成的缔合体进行了基态几何结构全优化，振动频率分析表明这些构型均为稳定的几何构型。分子间相互作用能的计算采用Boy和Bernardi提出的均衡校正方法以消除基组重叠误差，同时在相应基组水平下进行了零点能校正。采用Multiwfn程序[19]分析IPA和DCM的分子表面静电势以及缔合体中分子间相互作用的强度和类型。利用统计热力学方法计算缔合体在288.15 K～303.15 K范围的热力学性质。

2 超额摩尔体积和红外光谱分析

IPA、DCM及其组成的混合物在常压、不同温度及不同组成下的密度测定结果见表1。基于测定密度数据，不同组成混合物的超额摩尔体积（VE）由方程：

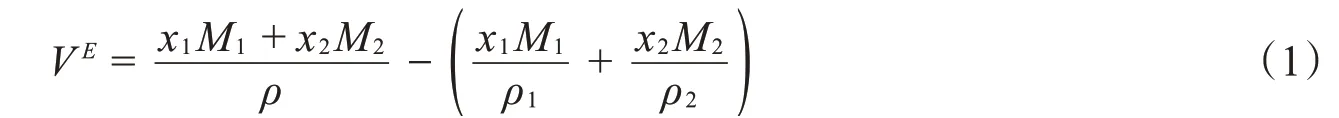
直接计算获得，其中，x1和x2分别为IPA和DCM的摩尔分数；M1和M2分别为IPA和DCM的摩尔质量；ρ、ρ1和ρ2分别为二元混合物、IPA和DCM的密度。VE的计算结果如表1所示。

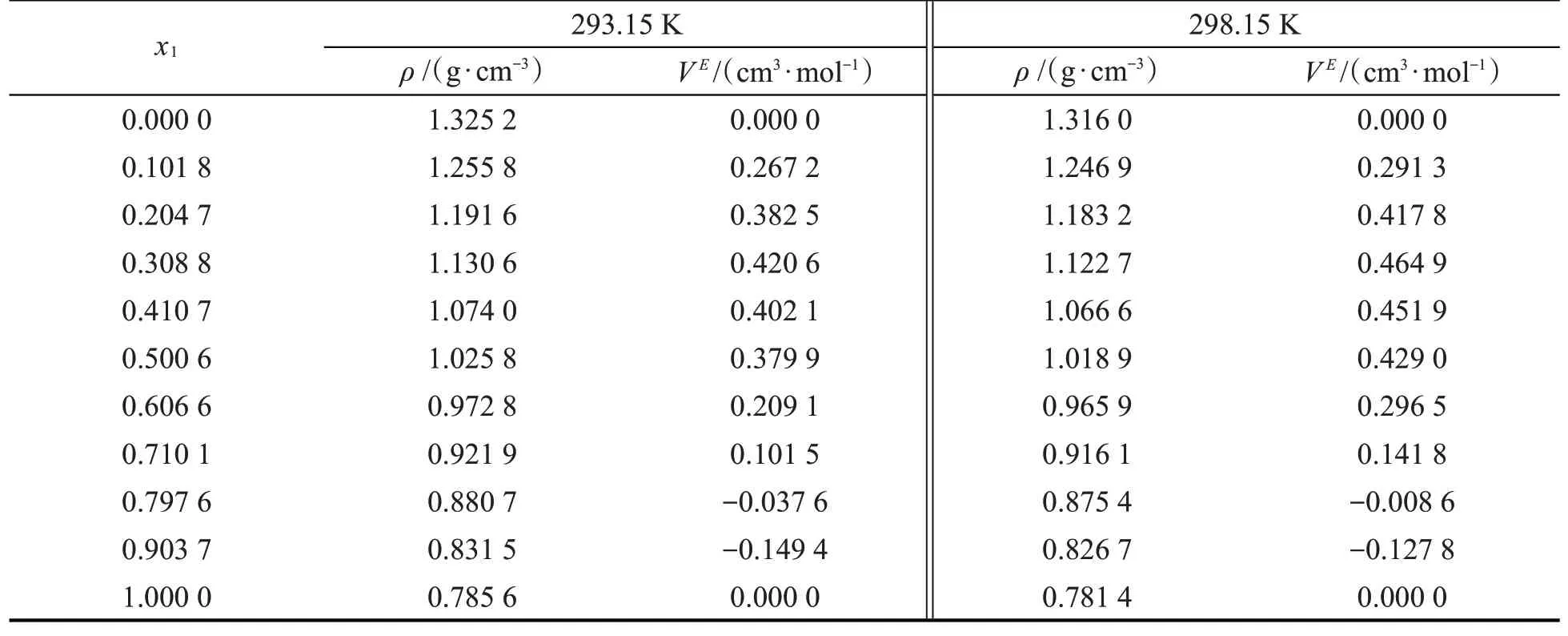
表1 二元混合物在不同温度下的密度和超额摩尔体积

混合物的VE与组成关系可以通过Redich-Kister方程关联。

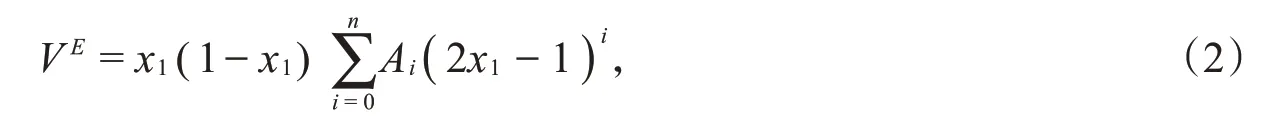
其中，x1为IPA的摩尔分数，Ai为最小二乘法拟合得到的关联系数。所有的拟合参数和标准偏差见表2。

表2 二元混合物的Redich-Kister方程拟合系数和标准偏差

从图1可见，IPA和DCM混合物的VE在低摩尔分数范围内均为正值，在较高摩尔分数范围内为负值。在不同温度下，混合物的VE变化趋势极相似，均呈不对称的S形曲线特征，且在组成一定的情况下随着温度的升高其VE绝对值在低摩尔分数范围内变大而在较高范围内变小。对于混合物，影响其VE的主要因素为各单体之间的化学、物理相互作用和结构特性。基于分子微观结构特征，IPA分子可以通过氢键（O-H…O）产生强自缔合作用，也可以和DCM分子通过氢键（C-H…O）或卤键（C-Cl…O）发生弱交叉缔合作用，而DCM分子间仅存在弱的自缔合作用。在低摩尔分数范围内，IPA与DCM分子间交叉缔合作用对VE的负贡献低于IPA分子间的解缔所引起的正贡献。而在较高摩尔分数范围内，足够多的IPA分子可以通过强自缔合作用形成氢键框架，而DCM分子可以填充在框架空隙中，此时体积填充效应对VE起负贡献，导致VE为负值。另外，从该混合物的VE与温度关系来看，随着温度升高，分子间缔合作用被削弱、距离增大，从而导致VE正偏差增大、负偏差减小，该结果表明温度也是影响VE的一个决定因素。

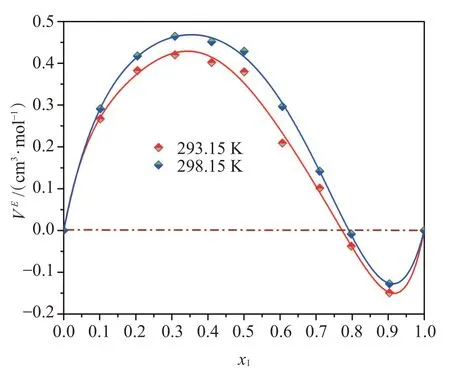
图1 二元混合物的超额摩尔体积随组成变化的关系图

红外光谱技术也可以方便、有力地揭示溶液分子间缔合作用。我们测定了室温下IPA、DCM及二者混合物的红外光谱。图2给出了在305 0 cm-1～355 0 cm-1间O-H键的伸缩振动吸收峰。可以看出，振动吸收峰的波数随着异丙醇摩尔分数的增大而减小。O-H键伸缩振动峰发生较大的红移表明在低摩尔分数时混合物中形成了IPA和DCM的交叉缔合体，而在较高摩尔分数时IPA分子间形成了强自缔合体。尤其是，在x1≈0.90时的混合物中O-H键伸缩振动峰的位置与异丙醇的基本一致，表明在此浓度下IPA形成了氢键框架。红外光谱分析结果也支持了超额摩尔体积的S形曲线变化特征。

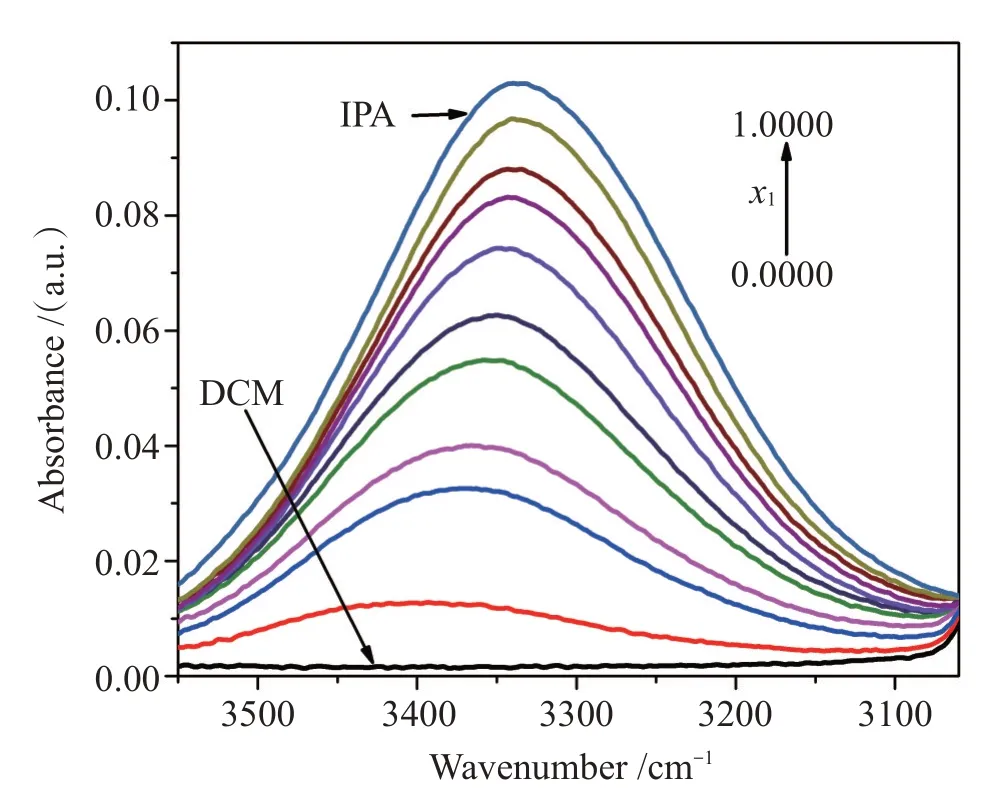
图2 异丙醇、二氯甲烷和二元混合物的红外光谱图

3 几何结构和电子密度拓扑分析

为了更好地理解IPA和DCM混合物的分子间缔合行为，进行了基于IPA和DCM分子表面静电势分析。图3为IPA和DCM的分子表面静电势图。对于IPA分子而言，其羟基氢原子和氧原子周围出现了静电势最大值和最小值位置，其静电势值分别为+40.39和-37.22 kcal·mol-1，另外IPA分子的其它原子也出现静电势极大值点。在DCM分子的氢原子和氯原子附近也出现了静电势最大值和最小值点，其值分别为29.14和-13.51 kcal·mol-1，在氯原子周围出现了σ空穴，其静电势值为8.43 kcal·mol-1。基于分子表面静电势分析表明混合物中IPA分子间可以通过强的O-H…O氢键形成自缔合体，而IPA和DCM分子间可通过C-H…O氢键或C-Cl…O卤键形成交叉缔合体，此外，DCM分子间也可以通过弱的C-H…Cl氢键形成自缔合体。

图3 异丙醇和二氯甲烷的分子静电势图

图4是在M06-2x-D3/6-311++G(d,p)水平上优化获得的4种稳定缔合体，相应结构参数见表3。可以看出，4种缔合体的氢键/卤键键长和键角数值均在典型氢键/卤键的范围内。此外，衡量化学键强度的特征参数ΔR（H/Cl…A）见表3，其数值大小可以用来预测键的强弱。在4个缔合体中，最大的ΔR（H…A）值为自缔合体I的O1-H…O2氢键，表明该氢键强度最大。因此，4个稳定缔合体中分子间化学键的强度顺序为

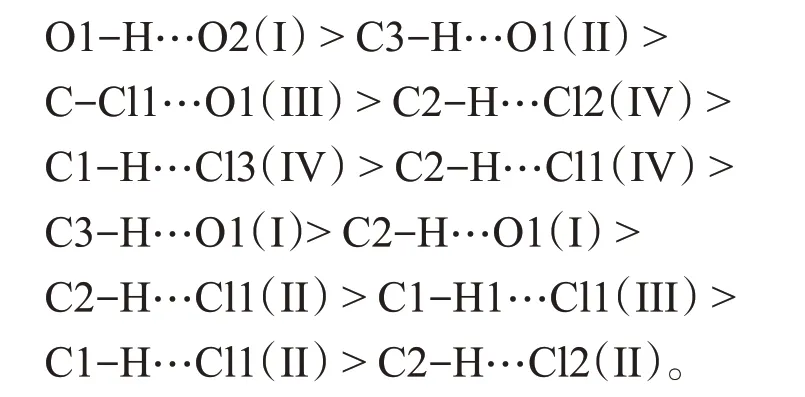
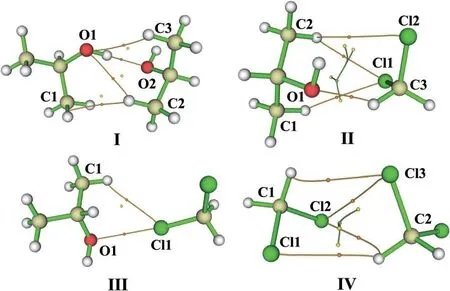
图4 4种稳定缔合体的分子拓扑图

表3 4种缔合体的氢键/卤键键长（Å）、键角（°）及其键临界点处的拓扑参数

利用分子中原子（AIM）理论方法研究了上述4个缔合体分子间相互作用的本质，其分子拓扑结构如图4所示，相应键临界点的特征参数电荷密度ρ(r)、拉普拉斯值▽2ρ(r)和总能量密度H(r)见表3。基于ρ(r)计算，4个稳定缔合体中分子间氢键/卤键的强度顺序和上述ΔR（H…A）分析结果一致。正的▽2ρ(r)和H(r)值表明4个缔合体的分子间作用均为闭壳层作用，是典型的非共价相互作用。这种非共价相互作用的可视化如图5和6所示，分别给出了优化缔合体的电子约化密度梯度散点图及其梯度等值面图（s=0.50 a.u.）。在sign(λ2)ρ=-0.027 3 a.u和-0.017 4 a.u处的尖峰分别表明形成了强的O1-H…O2（I）和C3-H…O1（II）氢键；在sign(λ2)ρ=-0.012 4 a.u处的尖峰表明缔合体III中存在C-Cl1…O1卤键作用。此外在sign(λ2)ρ=-0.005 a.u附近的尖峰表明4个缔合体中也存在弱的氢键作用和范德华吸引作用，而在sign(λ2)ρ=～0.005 a.u附近的尖峰表明4个缔合体中存在范德华排斥作用。电子约化密度梯度等值面图（图6）也表明4种缔合体中存在弱相互作用，蓝色圆盘状表明分子间形成了强的O1-H…O2（I）和C3-H…O1（II）氢键，绿色区域表明存在弱的氢键/卤键和范德华吸引作用，暗黄色区域表明缔合体中存在分子间的范德华排斥作用。该处分析结果和上述几何结构和电子拓扑分析结果相一致。

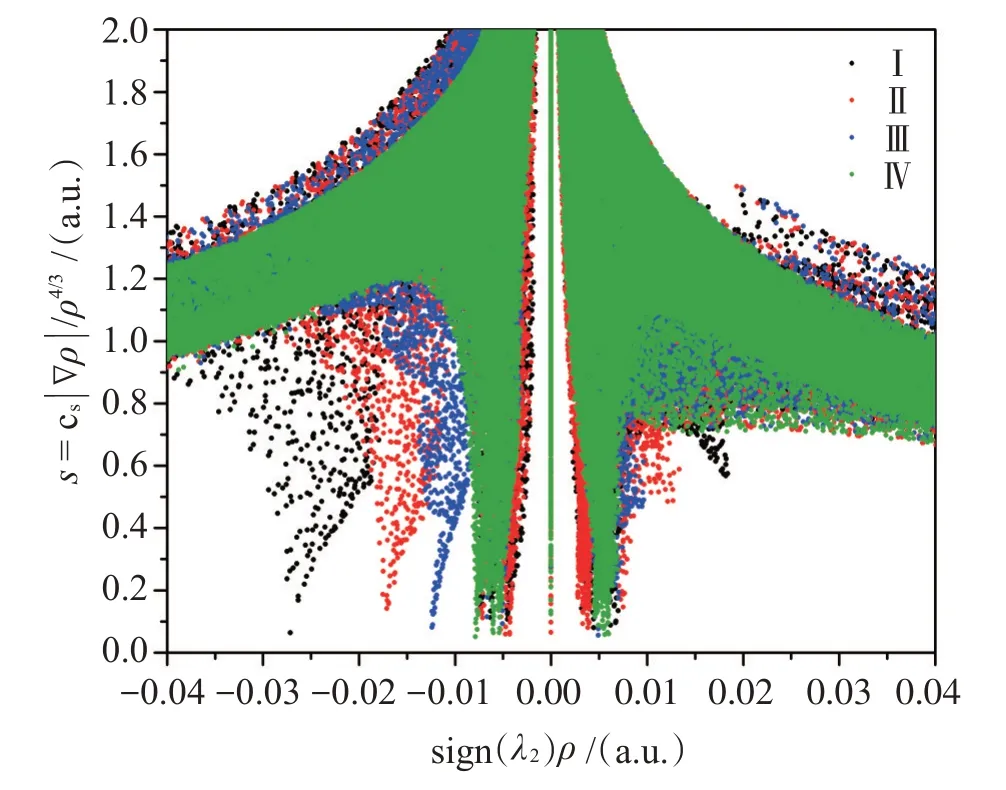
图5 4种缔合体的约化密度梯度函数散点图

图6 4种缔合体的约化密度梯度函数等值面图

4 分子间相互作用能和热力学函数分析

为了进一步研究含多个氢键/卤键的稳定缔合体中分子间作用机制，其分子间相互作用能的计算结果见表4。可以看出，4种缔合体的分子间相互作用能从小到大的顺序为I、II、IV、III，表明在二元混合物中IPA分子间的自缔合作用强于IPA与DCM间的交叉缔合作用。因此，在低摩尔分数范围内混合物的VE值为正值。在较高摩尔分数范围内，较多的IPA分子可以形成稳定的氢键框架，以及由于DCM的填充效应，导致混合物的VE为负值。上述分析结果和实验测定结果相一致。此外，基于振动和统计热力学分析，4种缔合体在288.15 K～303.15 K范围内的熵、焓和自由能的变化值见表5，可以看出形成缔合体的ΔST和ΔHT均为负值，表明由单体形成缔合体的过程是熵减、放热过程。同时，4种缔合体的熵和焓变化值均随温度升高而减小，表明该二元混合物的分子间相互作用随温度升高而变弱。此外，4种缔合体的ΔGT值均为正值，且随温度的升高而增大，表明4种缔合体的形成过程是非自发过程，所形成缔合体的稳定性随温度升高而逐渐降低，使得混合物的VE正偏差增大、负偏差减小，该结论和实验测定的结果一致。

表4 4种缔合体的分子间相互作用能（kJ·mol-1）

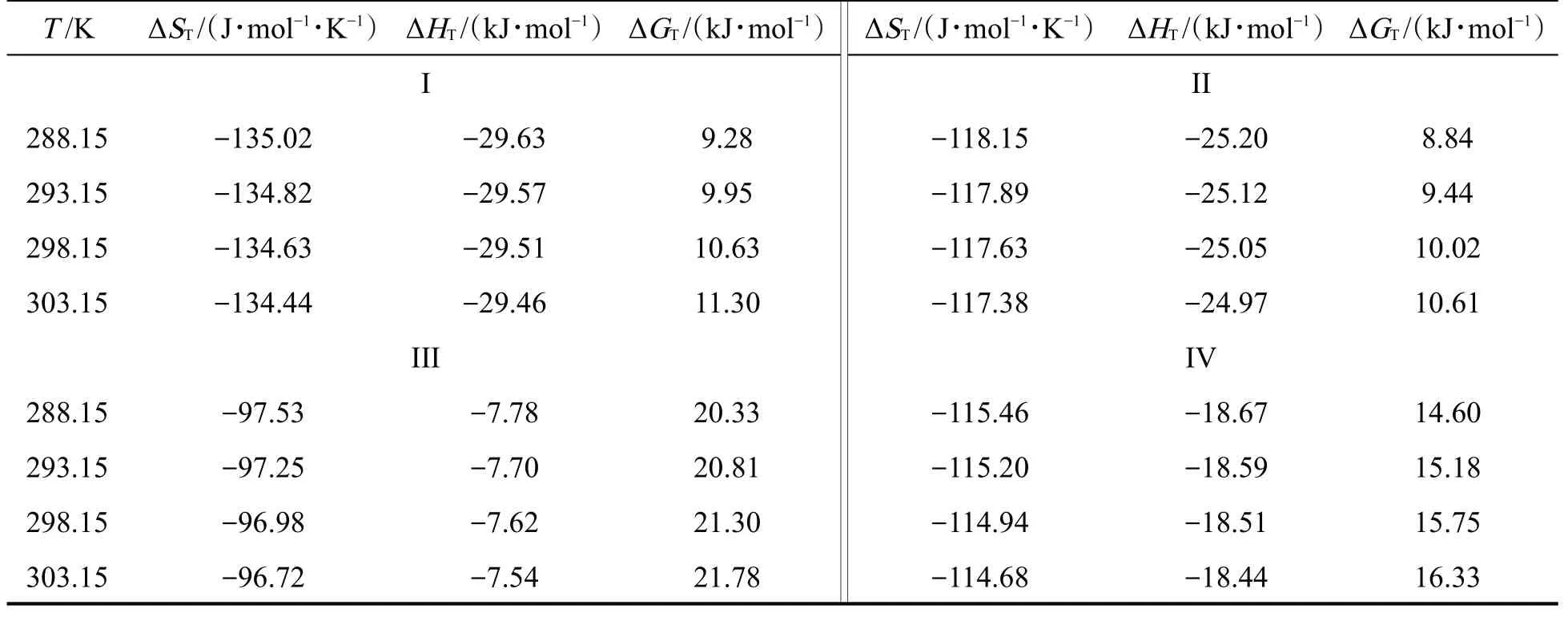
表5 4种缔合体在不同温度下的热力学性质

5 介电和玻璃化行为分析

图7给出了在273.15 K～298.15 K范围内低摩尔分数（x1≈0.25）和高摩尔分数（x1≈0.85）浓度的等温介电常数偏差随频率变化。其中，在x1≈0.25时的高频区域，除了在273.15 K时的介电常数偏差为负，其他3个温度下均为正偏差，且随温度升高偏差值增大；在低频区域，其介电常数偏差出现了极小值峰，且随温度升高峰值更负。而在x1≈0.85时的介电常数偏差变化特征不同于x1≈0.25时的变化特征。在高频区域的介电常数偏差均为负值，且随温度升高绝对值减小；在低频区域的介电常数偏差为正值，且随温度升高而增大。该二元混合物在高摩尔分数和低摩尔分数时介电常数偏差所表现出的不同特征主要由该混合物分子的不同堆积行为所致。

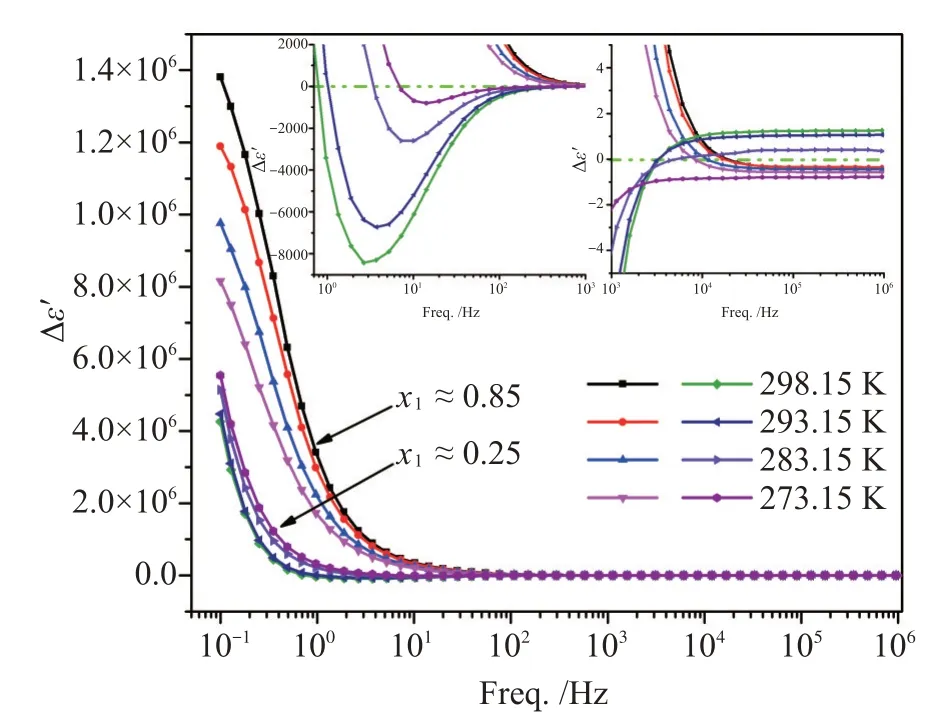
图7 二元混合物的等温介电常数偏差变化图

此外，还研究了该二元混合物在x1≈0.25和0.85摩尔分数时的等温介电损耗谱，分别如图8（a）（b）所示。可以发现，在低摩尔分数（x1≈0.25）和高摩尔分数（x1≈0.85）浓度时都只有一个动力学弛豫过程，且随温度升高，其弛豫峰位置从低频处逐渐向高频处移动。在相同温度下，x1≈0.85时其峰位置所在的频率小于x1≈0.25时峰的位置。采用Havriliak-Negai方程对这一弛豫过程进行拟合，获得了重要参数——弛豫时间。图8也给出了该二元混合物在两种浓度时的结构弛豫激活能谱曲线，揭示了结构弛豫时间随温度的变化关系。同时利用Vogel-Fucher-Tamman方程对弛豫时间（log10τ）和温度进行了拟合，图中黄色实线为拟合曲线，其拟合的方程分别为log10τ=-12.83+798.16/（T-55.66）（x1≈0.85）和log10τ=-10.95+171.74/（T-128.71）（x1≈0.25）。由于结构弛豫时间为100 s时的温度为动力学玻璃化转变温度，因此，由上述拟合方程计算了该二元混合物在x1≈0.85和0.25浓度时的玻璃化转变温度分别为109.48 K和141.97 K。介电损耗谱和结构弛豫激活能谱研究结果均表明该二元混合物在高摩尔分数和低摩尔分数时存在不同分子排列方式，这一研究结果和上述超额摩尔体积、红外光谱和理论计算结果均相一致。

图8 二元混合物的结构弛豫激活能谱，插图为等温介电损耗谱。（a）x1≈0.25；（b）x1≈0.85

6 结论

在常压下测定了IPA与DCM二元化合物在全摩尔分数范围内和不同温度下的密度，并计算了其超额摩尔体积，发现其呈不对称的S形曲线特征；在组成一定的情况下，随温度升高其超额摩尔体积绝对值在低摩尔分数范围内变大而在较高范围内变小。此外，结合红外光谱分析和密度泛函理论方法研究了该二元混合物的分子间相互作用。结果表明在二元混合物中IPA分子间的自缔合作用强于IPA与DCM分子间的交叉缔合作用。通过统计热力学方法研究了该二元混合物中形成的4种稳定二聚体的热力学性质，表明缔合体的形成过程是一个放热、熵减、非自发过程，其稳定性随温度升高而逐渐降低。研究了该二元混合物在摩尔分数为0.25和0.85时的介电行为和玻璃化转变温度，结果表明混合物组成对其结构和性质具有重要作用。