具有复合隔离策略的计算机病毒传播模型的时滞动力学研究

杨芳芳，张子振，段爱华，门秀萍

（安徽财经大学 管理科学与工程学院，安徽 蚌埠 233030）

随着网络规模的日益扩大[1]，计算机病毒的传播变得更加迅猛，为了更好地研究计算机病毒的传播机理，建立准确的计算机病毒传播模型是十分必要的。根据计算机病毒和生物病毒的相似性，CHEN和GAN建立了多个数学模型来研究计算机病毒的传播规律[2-3]，UMBREEN、YAO和ZHENG等将隔离策略应用到计算机病毒模型的研究中，并据此提出了一系列模型[4-6]，但是他们的模型没有考虑到各个状态的节点都以不同的概率被隔离。基于此，文献[7]提出了一类具有复合隔离策略的计算机病毒传播模型，但在建模过程中，假设处于恢复状态的计算机会直接转变为易感状态，忽略了临时免疫期时滞对计算机病毒传播的影响。考虑到这种情况，在文献[7]的基础上，本文建立了一个具有临时免疫期时滞和复合隔离策略的SLBQRS（Susceptible Latent Breaking out Quarantine Recovered Susceptible）计算机病毒传播模型：

建立上述模型时，做如下假设：（1）虽然易感状态、潜伏期状态和已感染状态的计算机都会以σ1、,σ2、σ3的概率被隔离，但是由于潜伏期状态和已感染状态的计算机已经携带病毒，他们会比易感染状态的计算机有更大概率被隔离，所以σ2＞σ1＞0,σ3＞σ1＞0；（2）处于恢复状态的计算机因为获得了临时免疫能力，在再次成为易感计算机前存在一个临时免疫期时滞τ，其中，τ为常数。

1 有毒平衡点稳定性和Hopf分岔存在性

根据文献[7]的分析，模型（1）有且仅有一个有毒平衡点E*(S*,L*,B*,Q*,R*)。令模型（1）的等式右边等于零，可求得：

由Routh-Hurwitz定理可知，如果假设G0成立，则方程（4）存在负实根，即当τ=0时，E*(S*,L*,B*,Q*,R*)是局部渐近稳定的。当τ＞0时，令λ=iω(ω＞0)为方程（3）的根，则

定理1如果假设G0～G2成立，当τ∈[0,τ0)时，时滞模型（1）在有毒平衡点E*(S*,L*,B*,Q*,R*)处是局部渐近稳定的；当τ≥τ0时，模型（1）产生Hopf分岔。

2 Hopf分岔的方向和周期解

规范型定理和中心流形定理是研究Hopf分岔性质的常用理论，基于此，本节采用文献[10-11]的方法对模型（1）的Hopf分岔方向和周期解进行分析。

定理2当μ2＞0时，模型（1）产生超临界Hopf分岔；当β2＜0时，模型（1）有稳定的分岔周期解；当T2＞0时，模型（1）的分岔周期是递增的。

3 数值模拟

为了验证上述结论的正确性，我们将以下实验数据带入模型（1）进行仿真实验：μ1=0.05，μ2=0.05，μ3=0.1，γ1=0.01，γ2=0.015，γ3=0.15，β1=0.01，β2=0.012，β3=0.085，η=0.000 2，σ1=0.01，σ2=0.025，σ3=0.015，α=0.060 4。利用Matlab软件进行数值模拟，仿真结果分别如图1所示。仿真实验模型有且仅有一个有毒平衡点E*(0.420 2,0.189 2,0.087 87,0.102 3,0.200 3)，进而计算得到τ0=18.990 5。由定理1可知，当τ∈[0,τ0)时，模型在有毒平衡点E*处局部渐近稳定；当τ的取值超越临界点τ0时，模型产生Hopf分岔。为验证定理1，我们选取不同的时滞进行仿真模拟。首先，考虑时滞小于临界值的情况，为此选取τ=17.560 5＜τ0进行仿真模拟，图1（a）（左列）展示了时滞小于临界值时S（t），L（t），B（t），Q（t），R（t）的变化情况，此时，仿真实验模型在有毒平衡点处局部渐近稳定。然后，考虑时滞大于临界值时的情况，为此选取τ=20.221＞τ0进行仿真模拟，图1（b）（右列）展示了时滞大于临界值时S（t），L（t），B（t），Q（t），R（t）的变化情况，仿真实验模型在有毒平衡点处产生Hopf分岔。

4 结论

综上所述，本文在文献[7]的基础上，考虑临时免疫期时滞，建立了更贴近实际情况的时滞SLBQRS计算机病毒传播模型，该模型充分考虑了杀毒软件的广泛利用对计算机病毒传播带来的影响，与计算机病毒的实际传播情况更吻合。首先，将临时免疫期时滞作为一个重要参数建立模型，通过分析模型特征根的分布情况，进一步得到模型的有毒平衡点和Hopf分岔条件，并计算得到有毒平衡点E*(S*,L*,B*,Q*,R*)和临界值τ0；然后，分析模型（1）的Hopf分岔性质；最后，为了验证结论的正确性，选取合适的数值进行仿真模拟。结果发现，当时滞τ在临界值之下时，系统逐渐趋于稳定，此时计算机病毒的控制效果更好；当时滞τ超过临界值τ0时，系统产生分岔，即计算机病毒将失去控制。综合考虑复合隔离策略与临时免疫期时滞，建立具有复合隔离策略的时滞SLBQRS模型，对于计算机病毒的防御和治理具有重要意义。但是在研究过程中仅仅考虑单一时滞造成的影响是不够的，在今后的研究中将综合考虑潜伏期时滞和临时免疫期时滞，研究具有双时滞的计算机病毒传播模型的动力学行为。

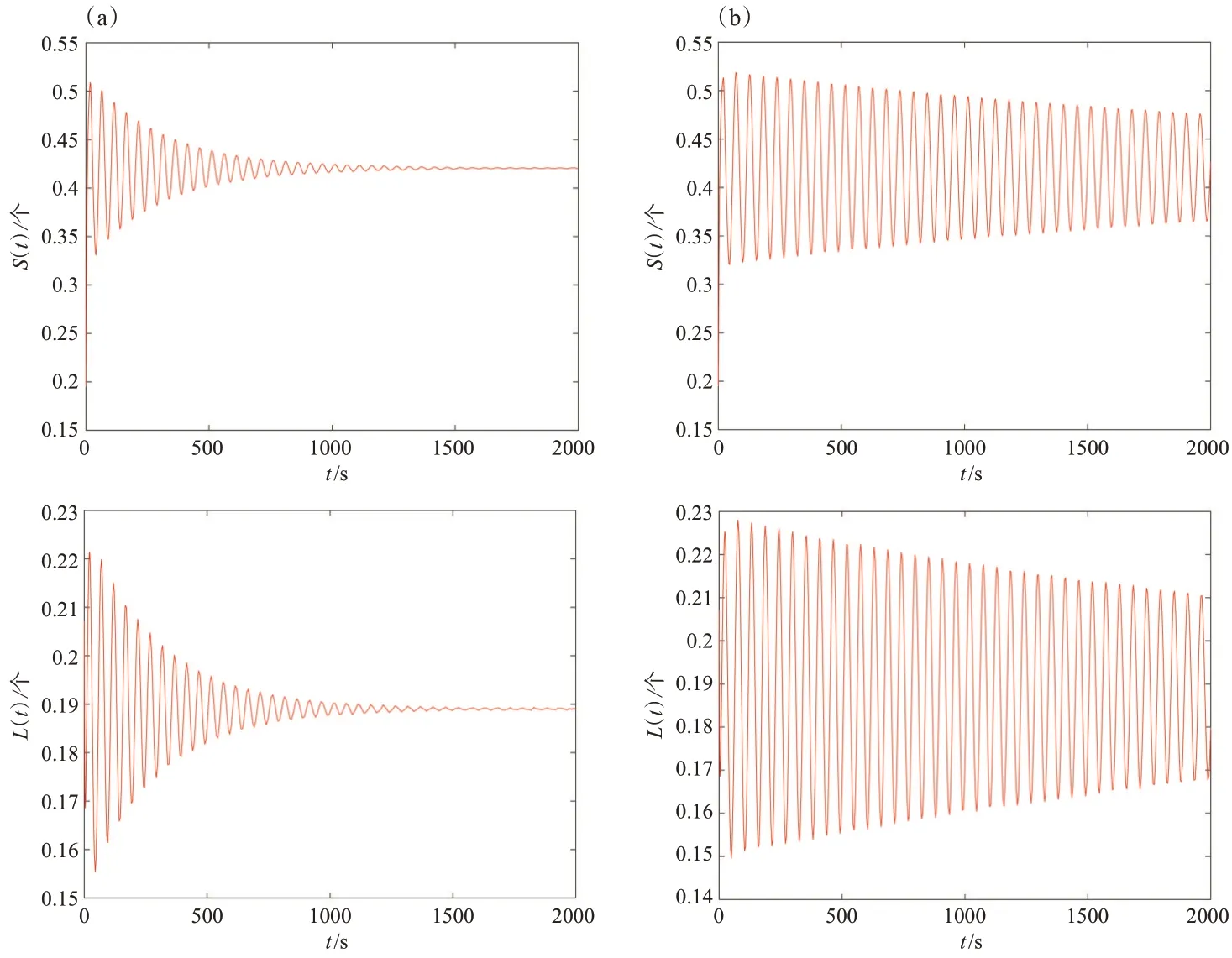
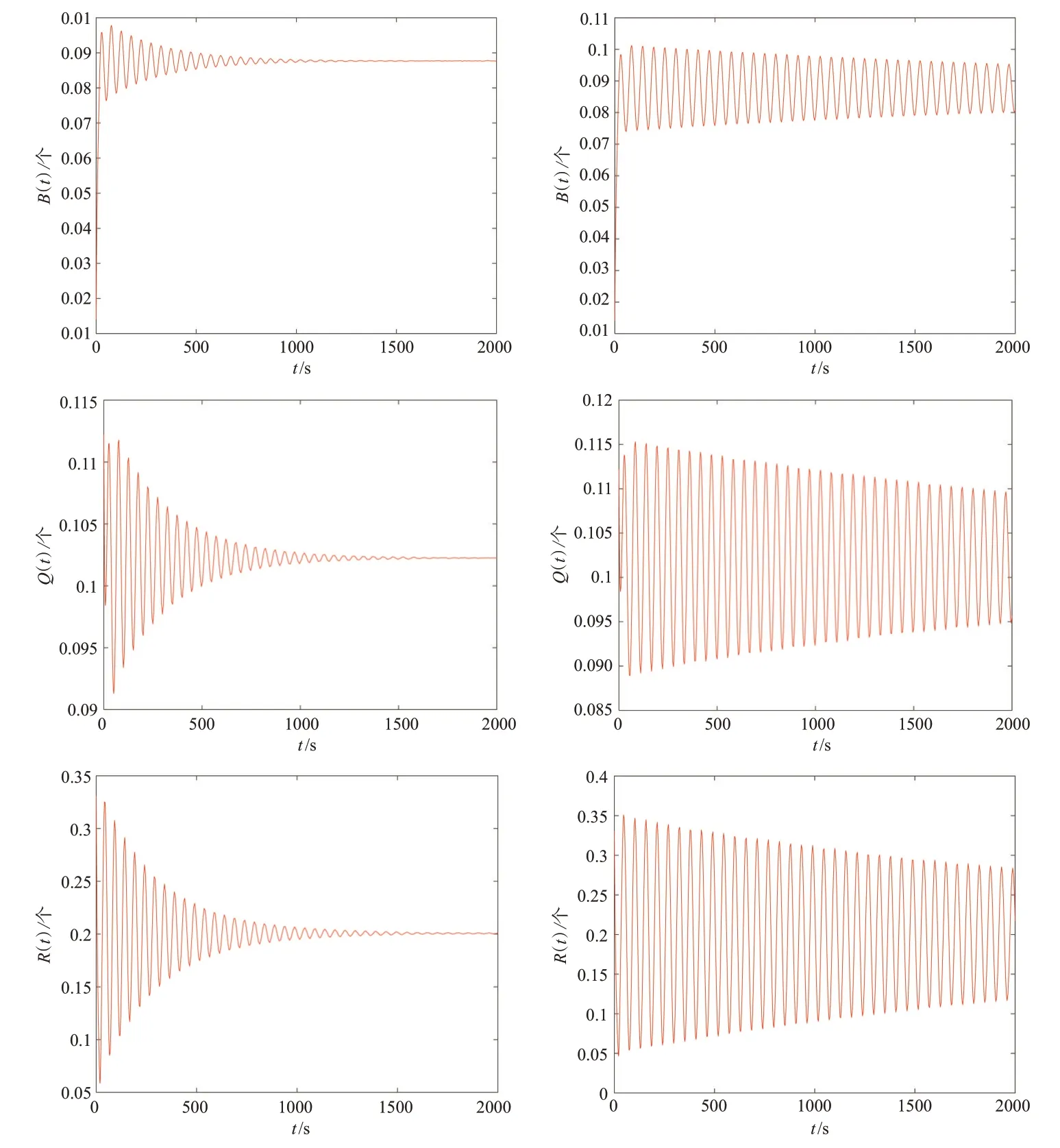
图1（a）τ＜τ0和（b）τ＞τ0时，S（t）、L（t）、B（t）、Q（t）、R（t）的变化情况