部分线性Logistic模型在大学生挂科率预测中的应用

赵 波, 卞纪兰， 王纯杰， 王淑影, 赵桂燕

(1.长春工业大学 数学与统计学院， 长春 130012；2.黑龙江八一农垦大学 经济管理学院， 大庆 163319)

0 引 言

近年来，随着我国高等教育由精英化教育转向大众化教育的转变，高校的高速度扩招，使得我国高等教育快速普及。但是，也不可避免地为高校的教育质量带来一些新的问题[1]。特别是当代大学生挂科(考试不及格)问题越发凸显。因此，如何预防学生挂科已经成为当前学生管理研究的主要任务之一。

截至目前，已有不少学者对当代大学生的挂科现象进行了分析。罗晨辉指出当代大学生受到物质和精神世界的双重诱惑，思想上对学习的过度轻视、学习的盲从等因素是造成大学生挂科的主要原因[2]；李丹花指出学习目标不明确，沉迷于网络、学习期间兼职打工以及为情所困，迷失自我是导致大学生挂科的主要原因[3]；高朋敏等从环境变化、目标缺失等方面揭示大学生的挂科原因[4]等等。这些文章均是通过定性分析方法得到的，因此缺少一些数据的支撑。当然，也有一些学者已经对其展开了定量分析，例如，马丹妮从机器学习角度建立了学生学业预警模型，通过分析统计某大学学生成绩等数据，分别实现学生课程挂科预测和学生毕业情况预测，从而实现异常学生学业预警[5]；张丽华等利用Logistic回归模型分析了大学数学考试成绩，发现学生入学高考成绩与性别对该校学生大学数学挂科有着显著性影响[6]；韦新星基于Logistic回归分析与判别分析相结合，对大学生挂科的预测问题进行研究，但是该文献中忽略了分类阈值选择以及忽略了连续变量对挂科概率的非现线性影响，因而造成信息的损失，以至于分类问题没有达到最优解[7]。

因此，本文将从定量分析的角度出发，结合东北地区高校管理背景，考虑非线性因素的影响，提出部分线性Logistic回归模型，并利用Sieve方法逼近非线性函数，基于极大似然推断模型参数。根据参数结果分析非线性函数以及其余分类变量对挂科概率的影响。最后画出ROC曲线说明该模型可以有效地分出挂科与不挂科的学生，约登指数为学生分类提供了一个最优的分类阈值。

1 数据来源及指标体系

从定量分析的角度，随机收取黑龙江某高校在校二年级学生对其挂科问题进行研究。原始数据来源于该校在校二年级学生的生活状况，以及该校的相关政策。将学生是否挂科作为因变量y，如果存在挂科，则y=1，如果没有挂科，则y=0。从学校的相关政策以及管理角度出发，为了分析学生挂科的情况，收集到138个样本，包括第二课堂成绩(课外成绩以及一些定性变量量化后的综合得分-由某高校的文件支撑)、性别、专业(收集到的数据中仅有两个专业，分为A类和B类)、恋爱情况、文科生还是理科生(抽样的班级高考录取时文理兼招)、高考生源所在地、兼职情况以及是否有逃课经历(不论请假与否，均视为旷课)等8个影响因素作为协变量，其中第二课堂成绩是根据在校学生在大二学年获得的奖项、荣誉以及参加学校、学院和班级活动情况的分值量化，有各项活动分的一个累积值，因此是一个取值大于0的连续变量(如果参加活动足够多，该变量的取值会足够大)，其他变量均是离散的分类变量。具体的变量取值及其对应含义如表1所示。

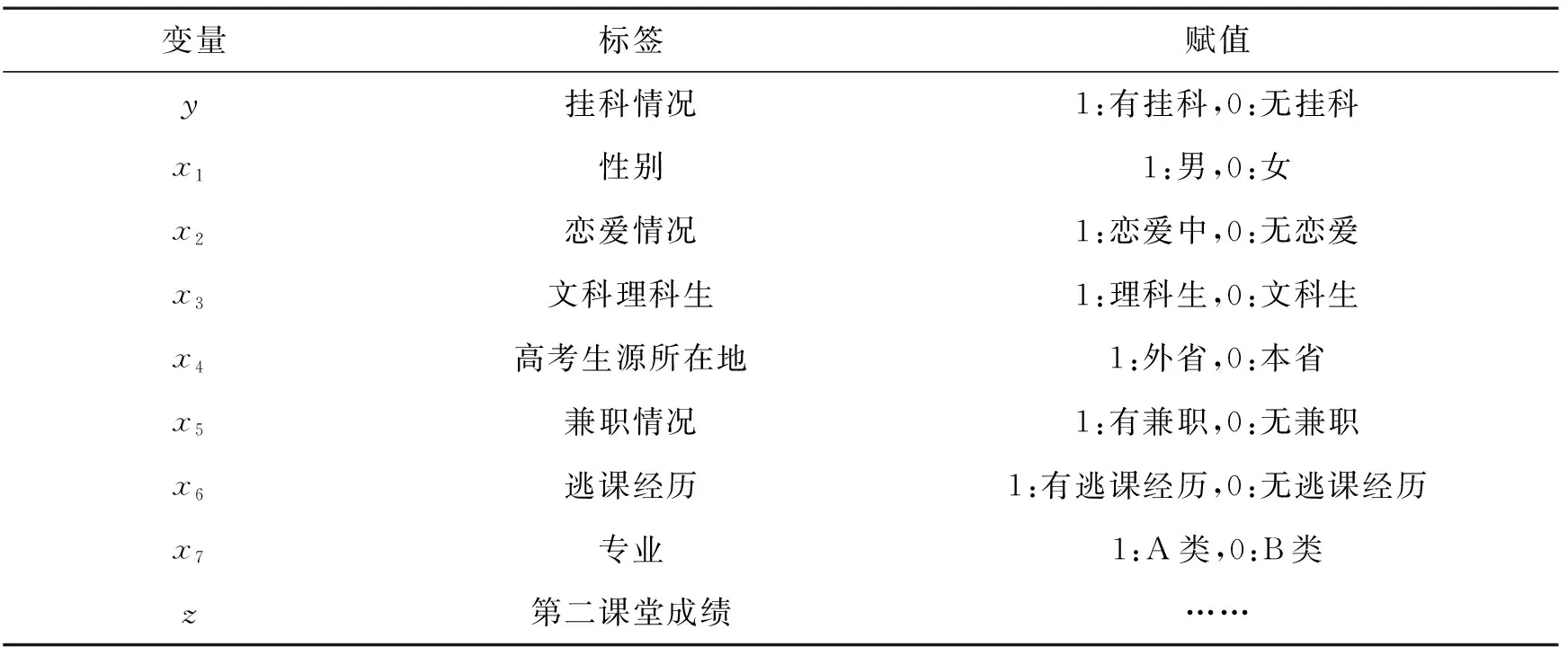
表1 变量取值及其对应含义

2 部分线性Logistic模型

Logistic回归分析是一种广义的线性预测回归模型[7]，在社会学、人口学、计量经济学、环境科学、医学、气象学以及生物学等领域有着广泛的应用[8-11]。假设y是感兴趣的0-1型变量，y=1表示设定的感兴趣的类别，发生的概率P(y=1)=π；y=0表示设定的不感兴趣的类别，发生的概率P(y=0)=1-π。传统的Logistic回归模型假设兴趣事件的概率与各个协变量之间呈现线性关系，因此Logistic模型的一般形式表示为：

(1)

然而，在实际应用中兴趣事件的概率受到一些非线性因素的影响，从而考虑下面部分线性Logistic回归模型：

(2)

式中：β0,β1,β2,…,βp-1,βp表示回归系数；x1,x2,…,xp-1,xp表示协变量；z表示连续型协变量；f(·)表示非线性函数。

在模型(2)下考虑样本量为n的样本，对个体i,i=1,2,…,n，则对数似然函数为：

(3)

为了估计非线性函数，选择Sieve方法[12-16]对未知函数f(z)逼近，具体过程如下：

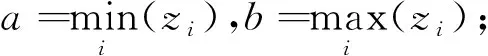
Step2： 在区间[a,b]生成B样条基函数Bj(z)，j=1,2,…,J;

Step3： 定义Sieve空间Φ={f(z):z∈[a,b],|f(z)|≤M,γ∈RJ}，其中

式中：γj(j=1,2,…,J)表示Sieve空间未知样条参数；M为预先设置的常数；J为满足增加速率为O(nυ)整数，且0<υ<0.5。

设θ=(β0,β1,β2,…,βp-1,βp,γ1,γ2,…,γJ-1,γJ)T，对数似然函数式(3)可以写作：

(4)

为了获得模型中的参数，考虑两阶段优化算法，推断模型参数，先优化回归参数，再优化出样条参数，具体过程如下：

Step1： 选择初始参数β(0)和γ(0);

Step2： 在第s+1次迭代步骤中，给定第s次迭代步骤γ的值γ(s)，更新β(s)为β(s+1);

Step3： 在第s+1次迭代步骤中，给定第s+1次迭代步骤β的值β(s+1)，更新γ(s)为γ(s+1);

Step4： 直至在给定的条件阈值下收敛，即‖θ(s+1)-θ(s)‖≤0.001。

式中k,l=1,2,…,p+J+1。

3 实证分析

3.1 结果及分析

基于部分线性Logistic回归来分析预测黑龙江某高校在校二年级学生挂科情况的影响因素，其中变量z表示第二课堂成绩，是连续型协变量。假设第二课堂成绩与挂科概率呈现的影响呈非线性关系，其余变量x1,x2,…,x7均是离散变量，与挂科概率呈线性关系。为了估计模型中的非线性函数，选择三次B样条，两个随机节点组成样条基函数[17-18]，即J=5，从而逼近未知函数。最后在部分线性模型下，基于R软件计算该模型参数估计，获得结果如表2与图1所示。为了研究数据与模型的适用程度，选择 Hosmer-Lemeshow(H-L)统计量检验模型的拟合优度[19]，且计算得H-L统计量的值为4.012 7，P值=0.856，所以部分线性Logistic回归模型对实际数据拟合度较高，可以有效地应用该结果来预测该校二年级学生是否属于挂科类，从而给予警示。

表2 部分线性Logistic模型分析结果

由表2可知，在部分线性Logistic回归模型下，所收集到的138个数据中，x1(性别)所对应的回归系数β1=4.476 8，标准差为1.355，P值=0.000 95，因此在给定显著性水平α=0.05时，性别对挂科概率有着显著的影响，表明在控制其他因素的情况下，男性的挂科率远高于女性；x6(逃课经历)对应的回归系数β6=6.306 3，标准差为1.572 5，P值=0.000 06，因此在给定显著性水平α=0.05时，逃课经历对挂科概率有着显著的影响，且在控制其他因素的情况下，存在逃课经历的学生的挂科率远高于从没逃课的学生；x7(专业) 对应的回归系数β7=-2.094 8，标准差为0.882 7，P值=0.017 63，因此在给定显著性水平α=0.05时，不同专业的班级对挂科概率有着显著的影响，且在控制其他因素的情况下，专业A类的学生的挂科率远低于专业B类的学生；大学生时代是否恋爱、考生属于文科考生还是理科考生、是本省考生还是外省考生以及是否在校内外兼职等变量对应的P值均大于给定显著性水平(α=0.05)，因此在误差允许的范围内，这些变量对于挂科概率并没有显著影响。

第二课堂成绩的函数曲线如图1所示，在有限的样本下，函数曲线的单调性先增加，再降低，后平稳，最后又增加。第二课堂成绩对于挂科概率的影响具有波动性，先增加，再降低，平稳，最后上升。第二课堂成绩主要是基于各种活动与荣誉获奖加分获得的，因此，若要取得高分需花费大量的时间去参与各项活动，第二课堂成绩较低时，学生花费的时间很少，可能会增加学生的惰性。因此，为了更好地促使学生发挥主观能动性，主动学习，避免学生有过高的挂科率，应该设置合理的取值范围(如图1中展示的15至35分)，从而实现学生积极参与活动时间与投入学习时间的平衡。即在保证锻炼自身能力的同时，还要保证充分有效的学习时间，从而降低学生挂科概率。

图1 第二课堂成绩函数曲线

3.2 分类判别

在二分类问题的预测问题中，结果仅可能出现四种：(1)真正类(TP)-样本点属于正类并且被预测为正类；(2)假正类(FP)-样本点属于负类且被预测为正类；(3)真负类(TN)-样本点属于负类且被预测为负类；(4)假负类(FN)-样本点属于正类且被预测为负类。根据这四种情况可得表3。

表3 混淆矩阵以及评价标准

因此，在表3中可得分类模型整体正确率为：

(5)

基于部分线性Logistic回归模型结合判别分析分类方法[6,20]，根据学生平时的情况，计算学生挂科的概率，选择阈值p0将学生分为挂科与不挂科两类，预测学生是否具有挂科的危险，从而给予警示。因此选取合理阈值p0，当计算的学生的挂科概率大于p0时，视为学生具有挂科的危险；当计算的学生的挂科概率小于p0时，认为学生不存在挂科危险。基于收集到的样本数据，为了找到合理的p0，给出ROC曲线(图2)、灵敏度指数曲线(图3)、特异度指数曲线(图4)以及约登指数曲线(图5)。

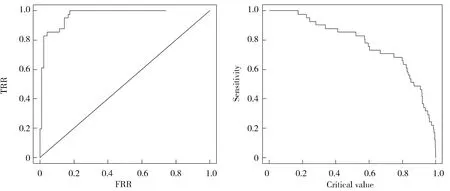
图2 ROC曲线 图3 灵敏度指数

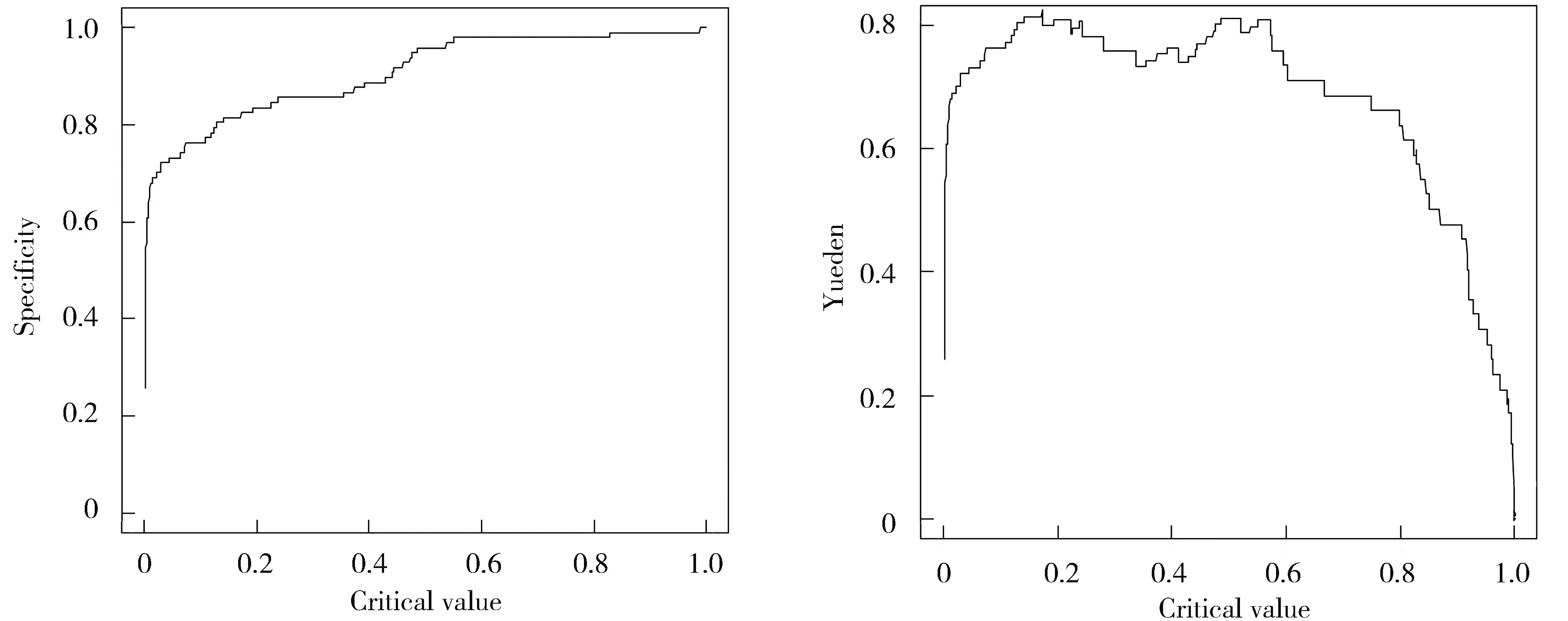
图4 特异度指数 图5 约登指数

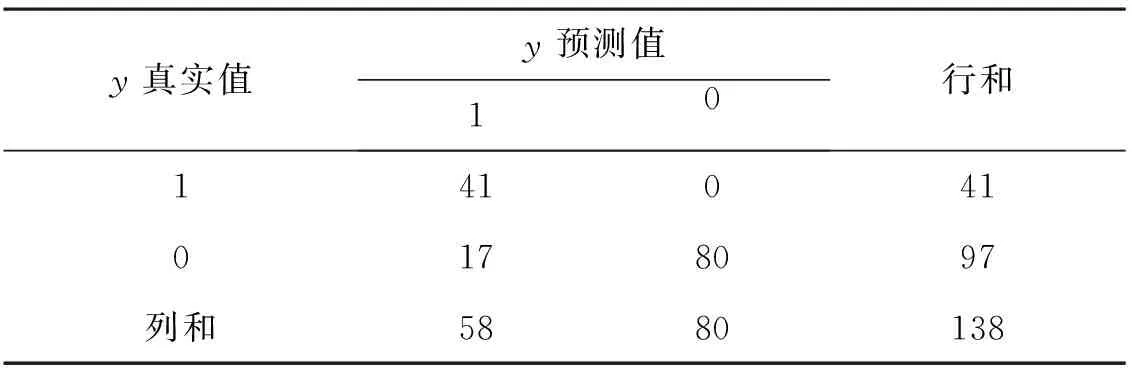
表4 分类预测结果

为了获得合理的阈值，使得阈值p0从0到1移动获得FPR(第一类错误的概率=1-specificity(特异度))以及TPR(Sensitivity(灵敏度)=1-第二类错误的概率)。以FPR为横轴、TPR为纵轴可得ROC曲线图如图2所示。ROC曲线下方的区域面积(Area under the ROC Curve，AUC)包含了分类时取不同阈值时的可能变现，其面积越大模型用来预测的效果越好，且图中AUC>0.5，接近于1，说明该模型有很好的优势；根据灵敏度指数图3与特异度指数图4定义约登指数=灵敏度+特异度-1，获得约登指数图5，优化出约登指数跳跃最大的点对应的概率值作为阈值p0=0.172。根据阈值p0=0.172区分出学生是否挂科的类别，预测结果如表4所示。根据预测结果表4以及式(5)计算的该模型分类的准确率为:

4 结 论

利用部分线性Logistic回归模型来定量分析大学生挂科的影响。运用三次样条逼近非线性函数，并基于极大似然推断模型参数。从推断结果可知，学生的性别、专业、逃课情况对挂科有着显著影响；第二课堂成绩在一定范围内可降低挂科概率；大学生时代是否恋爱、考生属于文科考生还是理科考生、是本省考生还是外省考生以及是否在校内外兼职因素对于挂科概率没有显著影响。

同时，依赖于部分线性Logistic回归模型分类预警学生是否有挂科危险，进而有利于学校及学生自身采取相应的措施来防止学生发生挂科。为了验证该方法分类的优越性以及后分类的最优阈值，给出了ROC曲线图以及约登指数图，继而获得最优分类器。

最后，基于部分线性Logistic回归模型分类的结果，为控制学生挂科率，给出以下建议：(1)应对男生给予更多关注，给予适当的帮扶；(2)考虑不同专业学生相同课程的大纲要求不同，应给予不同的考核方式或者考核内容；(3)加强学生的缺课管理，降低缺课次数；(4)适当控制第二课堂任务量，给出有效的第二课堂成绩区间。