一种多策略的变异果蝇优化算法

吴经纬，余玲珍，龙道银，杨 靖*

(1. 贵州大学电气工程学院，贵州 贵阳 550025;2. 中国电建集团贵州工程有限公司，贵州 贵阳 550001)

1 引言

果蝇优化算法(FOA)是一种通过模拟果蝇觅食行为来寻找全局最优解的群体智能算法[1]。与其它群体智能算法比较，FOA具有机制结构简单、代码易于实现、调节参数较少[2]的优点。当前，FOA已被成功应用于多核相关向量机预测模型[3]、模拟电路故障诊断[4]、传感器网络节点定位[5]、路径覆盖测试[6]等方面，具有很好的应用前景。

FOA算法由于优化过程中的随机性，在搜寻过程中存在盲目搜索，会导致算法早熟收敛、陷入局部最优。与其它典型群体智能算法类似，FOA算法相关参数的设置决定了该算法的性能。为了改善原算法的性能，文献[7]利用混沌映射所产生的混沌现象具有良好的遍历性、多样性的特点来改进果蝇算法的固定步长，在一定程度上提高了果蝇优化算法的优化性能；文献[8]从搜索方向的自适应选择机制、迭代步长值的自适应调整机制、自适应交叉变异机制和多子群机制四个方面对基本FOA算法进行改进，但该算法的复杂度较高；文献[9]在寻优过程中引入动态步长因子对基本果蝇优化算法的步长实现持续动态更新；文献[10]根据种群进化信息动态调整进化指导方向和搜索步长，但相对标准FOA算法需要较长的运行时间；文献[11]对果蝇个体的寻优步长进行了适应性的改变，但在多峰函数的寻优求解中得到的结果不太理想。

在上述研究基础之上，本文提出一种多策略的变异果蝇优化算法。首先，利用混沌映射的遍历性和随机性初始化果蝇种群，提高种群的多样性；其次，对寻优过程的随机步长引入可调整的动态变化收敛因子，有效平衡局部和全局搜索能力；最后，对寻优迭代中最优果蝇个体位置引入柯西变异保证群体的多样性，防止陷入局部最优。这些改进能有效地均衡果蝇优化算法的全局搜索与局部开发能力，提高了算法的收敛速度和寻优精度。

2 果蝇优化算法

果蝇在嗅觉和视觉上比其它物种有一定的优势。在寻找食物的过程中，首先，果蝇通过收集空气中不同的气味来寻找可能的食物来源；然后，果蝇群逐渐接近最佳气味浓度的位置；最后，它们可以通过敏锐的视觉来确定食物来源的准确位置，如此循环直到找到食物为止[12]。

FOA可以总结为7个步骤：

步骤1：初始化参数：种群规模数N、最大迭代次数Maxt和随机初始化果蝇群体位置X＿axis、Y＿axis。

步骤2：给果蝇方向和距离分配随机搜索的方向和距离

(1)

步骤3：估算果蝇与原点之间距离Di，再计算味道浓度判定值Si

(2)

Si=1/Di

(3)

步骤4： 将Si分别代入味道浓度判定函数，求出果蝇位置味道浓度Smelli

Smelli=Function(Si)

(4)

步骤5：寻找该果蝇群体中味道浓度(适应度)最佳的果蝇个体：

[bestSmell，bestIndex]=min(Smell)

(5)

步骤6：根据最佳果蝇位置，此时所有果蝇利用视觉向最佳位置飞去：

(6)

步骤7：最后迭代运算，重复步骤2～步骤5，在寻优过程中判断当前最佳味道浓度是否优于上一迭代结果，且判断当前迭代次数是否小于最大迭代数；若是则执行步骤6，否则结束。

3 改进的果蝇优化算法(MFOA)

3.1 基于混沌的种群初始化

FOA算法在解决函数优化问题中，一般利用随机产生的数据作为初始种群信息，虽在一定程度上保证了初始位置的均匀分布，但难以保留种群的多样性，导致算法的寻优效果较差。混沌是一种复杂的非线性系统动态行为，具有遍历性、随机性和规律性的特点，这些特点能够使算法容易逃离局部最优解，维持果蝇种群的多样性，同时提高全局搜索能力。

其思想即把果蝇种群的位置通过混沌映射线性地映射到混沌变量中，再根据混沌的特点优化搜索，最后将得到的解线性地转化到种群的变量空间中，从而使果蝇种群的初始位置分布更加均匀。

3.2 非线性控制策略

如式(1)所示，FOA在进行寻优时，果蝇的飞行方向和飞行距离都是随机的，导致FOA的寻优结果不稳定且易陷入局部最优。本文的改进思想是在算法执行的初期着重于全局搜索，以保证广泛的搜索范围，在算法执行的后期着重于精细的局部搜索，即针对最佳果蝇个体周围邻域进行搜索，以提高算法的寻优精度，从而实现全局搜索能力和局部寻优的动态平衡。因此本文在迭代过程中采用非线性调整策略更新果蝇个体位置：

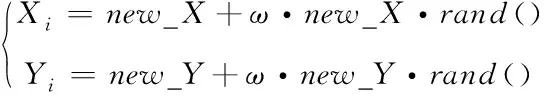
(7)

式中，new＿X和new＿Y为上一代最佳果蝇个体位置；ω为非线性动态变化收敛因子，公式如下

(8)

式中，ω1和ω2分别是ω的初始值和终值，经大量实验，ω∈[1，100]；μ是收敛调整因子，0<μ<1称为对数压缩因子，μ>1称为对数膨胀因子。图1是μ=1、Maxt=1000时的迭代次数与收敛因子的关系曲线图。

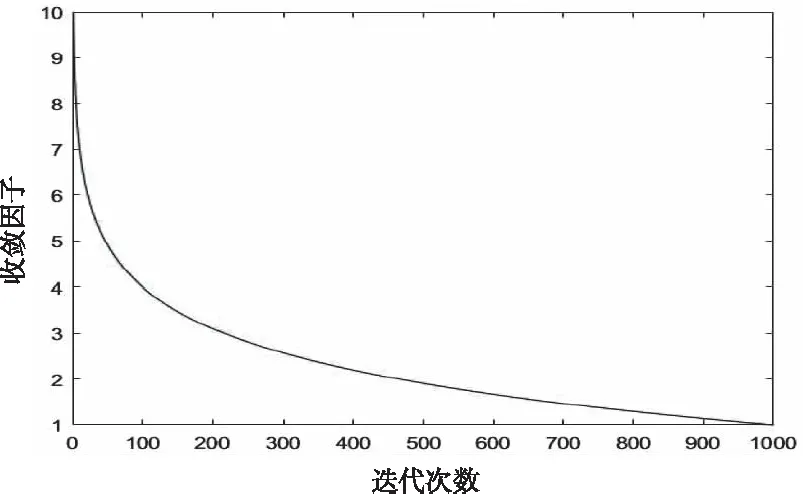
图1 收敛因子递减规律曲线

从图1可知，当μ=1，ω1=10，ω2=1时，在前期对数递减策略ω减小的趋势很快，如果找到适当的果蝇最佳位置就可以在局部进行精细搜索。本文μ=1，在实际工程应用中，对不同的优化问题可以适当的调整μ的值。

式(7)中将上一代最佳果蝇位置作为迭代寻优的起始位置，此策略既保持了围绕果蝇种群最优值分布的特点，又可通过动态变化收敛因子控制种群的全局搜索和局部开发。

式(8)功能如下：在算法的迭代前期果蝇具有较强的全局搜索能力，ω1取一个较大值来保证果蝇广泛的搜索范围，ω2取一个适当小的值，使得算法的迭代后期着重于精细的局部搜索。

3.3 柯西变异

种群中所有果蝇个体在进入迭代寻优时均向最优个体靠近，从而导致群体多样性的缺失，容易陷入局部最优，为了避免这种情况的出现，对其中最优果蝇个体进行柯西变异，增加种群的多样性。柯西分布和正态分布的概率密度函数曲线如图2所示，柯西分布在0处的峰值比正态分布小，果蝇个体会使用相对较少的时间来搜索相邻区间，从峰值到0值下降趋势比起正态分布更平缓，趋向于零的速度更慢，因此柯西变异的扰动能力更强，更容易产生远离原点的随机数，变异后的个体较容易跳出局部极值[13]。

图2 概率密度函数曲线

基本果蝇优化算法根据最优个体来更新下一代自身的位置，对最优个体提出的柯西变异策略表达式为

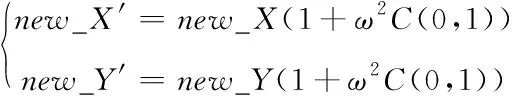
(9)

式中，new＿X和new＿Y为当前最优个体位置，new＿X′和new＿Y′为变异后的最佳果蝇个体位置；ω为2.2节的非线性动态变化收敛因子，利用ω的自适应能力来达到增强及减小变异扰动的作用；C(0，1)为以0为中心，尺度参数为1的柯西分布的随机数。

3.4 算法步骤

本文将混沌映射和非线性调整策略以及柯西变异的果蝇算法定义为MFOA，改进后的MFOA算法的具体步骤如下：

步骤1：初始化参数：种群规模数N，最大迭代数Maxt，收敛因子初终值ω1和ω2，维度d。

步骤2：利用混沌映射初始化果蝇种群位置。

步骤3：根据式(2)估算果蝇与原点之间距离Di，再根据式(3)计算味道浓度判定值Si。

步骤4：根据最佳果蝇位置，此时所有果蝇利用视觉向最佳位置飞去。

步骤5：根据式(8)生成动态变化收敛因子，按式(9)对当前最佳果蝇个体位置进行柯西变异。

步骤6：进入迭代运算后，按式(7)对果蝇种群位置进行更新，重复步骤3～步骤5，在寻优过程中判断当前最佳味道浓度是否优于上一迭代结果，且判断当前迭代次数是否小于最大迭代数；若是则执行步骤5，否则结束。

3.5 算法复杂度分析

时间复杂度是衡量寻优算法性能优劣的重要指标之一，主要取决于问题重复执行的次数。果蝇优化算法FOA的计算复杂度主要包括个体位置更新 、浓度值计算和适应度评估，假设种群规模为N，最大迭代次数M，维数d，个体浓度更新计算量为O(1)，所以FOA的时间复杂度为O(N ×M)。

本文改进的算法中，在FOA的基础上增加了混沌初始化种群位置，生成果蝇初始位置阶段的时间复杂度为O(N×d)；生成动态变化收敛因子ω的时间复杂度为O(M)，对最佳果蝇个体进行柯西变异的时间复杂度为O(M)，更新果蝇位置阶段的时间复杂度为O(M×(N+2))。

4 仿真分析

4.1 仿真场景设置

本文采用如表1所示的8个基准测试函数来评估MFOA算法性能。

表1 测试函数及参数设定

实验参数：种群规模N=30，最大迭代次数Maxt=1000。本文算法具体参数设置为：ω1=10，ω2=1。所有算法采用Matlab R2016b进行编程，计算机配置为：Intel Core(TM) i5-8250U、1.6GHz、4GB内存、Windows10操作系统。

实验内容：①将4种混沌映射初始化果蝇种群的优化结果进行对比实验，以确定性能最佳的混沌映射；②固定进化迭代次数，评估算法的收敛速度和寻优精度，并与FOA、ABC算法和其它参考文献的改进果蝇算法进行性能对比；③评估算法在高维、多峰函数上的性能，并与FOA算法和其它参考文献算法进行比较分析。

实验评价标准：实验中各算法独立运行20次，设置终止条件为迭代次数达到1000次。为评价算法的优化效果，本文给出如下三个判定标准：1)优化均值(MEAN)，用来衡量算法寻优的平均质量；2)标准差(STD)，评价算法寻优的稳定性；3)全局最优解(BEST)；4)达到最优适应度值所需平均迭代次数(以下简述为迭代次数)。

4.2 不同混沌映射的性能对比

为了验证不同混沌映射初始化果蝇种群的优化性能，使用了4种常见的一维混沌映射函数，如表2所示。

表2 常用的一维混沌映射

8个测试函数的进化迭代次数固定为1000，分别采用表2的常用一维混沌映射对果蝇种群进行初始化，各算法独立运行20次，其实验结果如表3所示。

表3 混沌映射优化的性能比较

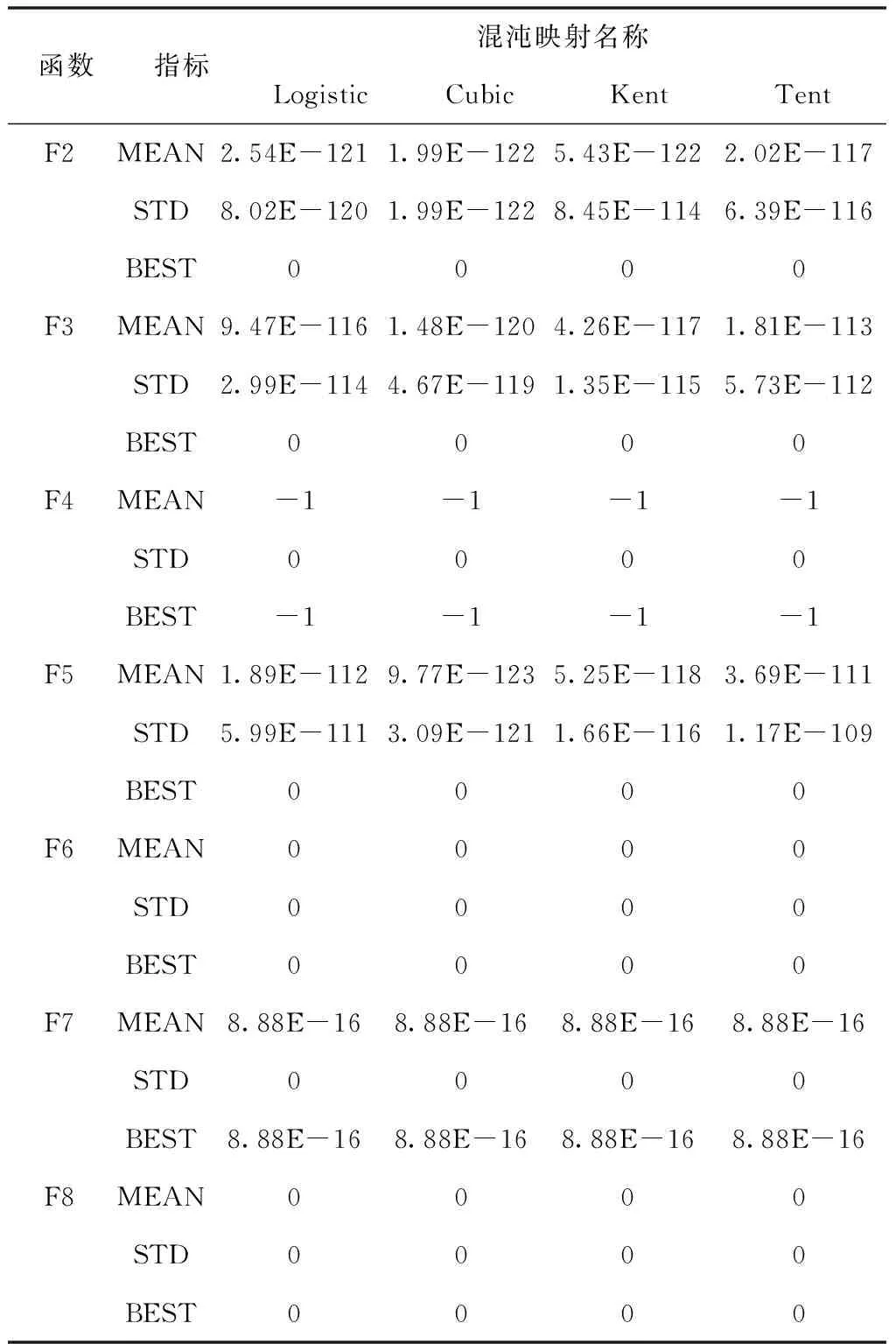
函数指标混沌映射名称LogisticCubicKentTentF2MEAN2.54E-1211.99E-1225.43E-1222.02E-117STD8.02E-1201.99E-1228.45E-1146.39E-116BEST0000F3MEAN9.47E-1161.48E-1204.26E-1171.81E-113STD2.99E-1144.67E-1191.35E-1155.73E-112BEST0000F4MEAN-1-1-1-1STD0000BEST-1-1-1-1F5MEAN1.89E-1129.77E-1235.25E-1183.69E-111STD5.99E-1113.09E-1211.66E-1161.17E-109BEST0000F6MEAN0000STD0000BEST0000F7MEAN8.88E-168.88E-168.88E-168.88E-16STD0000BEST8.88E-168.88E-168.88E-168.88E-16F8MEAN0000STD0000BEST0000

由表3可知，综合优化均值、平均值和全局最优解这三个评价指标，与其它三种混沌映射相比，基于Cubic混沌映射的果蝇初始化种群的整体性能更好，更接近理论极值，具有更高的精度和稳定性，也进一步说明混沌映射初始化种群的可行性和有效性。

4.3 收敛速度和寻优精度分析

将8个测试函数F1～F8固定迭代次数为1000次，分别采用FOA、ABC、文献[14]中的WFOA算法、文献[15]中的CSFOA算法和本文算法MFOA经过20次独立运行，其中人工蜂群算法ABC算法参数设置为：试验极限次数limit=60；其它参考文献算法按照原文献进行设置。分别将运行得到的优化均值(MEAN)、标准差(STD)、最优值(BEST)和迭代次数来表征，维数均设置为30，得到的实验结果如表4所示。

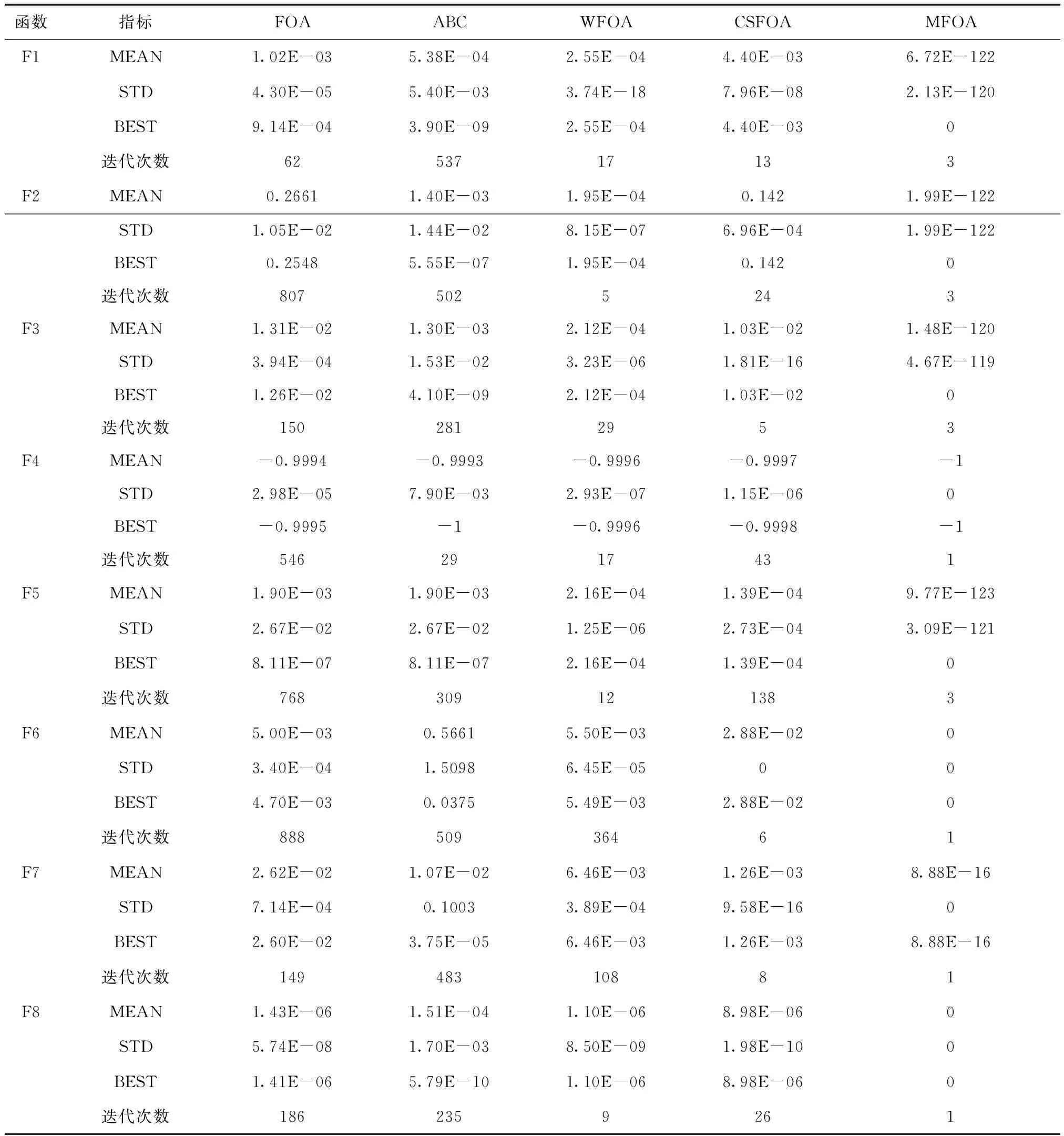
表4 五种算法的性能比较

由表4可知，当维数为30时，MFOA算法在F1～F3和F5测试函数上所得的优化均值(MEAN)更加理想，至少提高了118个数量级，虽然对于复杂的多峰函数F7来说，只是提高了14个数量级，但对于F4、F6和F8测试函数来说，MFOA算法均达到了理论极值，说明MFOA算法具有较好的优化精度；在F1～F3和F5测试函数上所得的测试标准差(STD)，MFOA算法相比其它四种算法更加理想，至少提高了102个数量级，对于多峰测试函数F6～F8和单峰函数F4来说，MFOA算法的STD达到了最优，说明MFOA算法具有较强的鲁棒性；并且在8个测试函数中，MFOA算法相比其它四种算法具有最优的BEST指标，迭代次数也最少，表明改进算法保证了较好的最优预测性能和较快的收敛速度。

总而言之，在测试函数F1～F8中，MFOA获得的MEAN、STD、BEST和迭代次数这四个测试指标均优于其它四种算法，这充分验证了相比这四种算法，MFOA在收敛速度、寻优精度以及算法的稳定性上都有很大的提升，说明改进算法不仅对单峰测试函数具有较好的寻优精度，而且对多峰函数也表现出较好的寻优性能和收敛速度，进一步验证了MFOA算法的优良寻优性能。

五种算法的迭代寻优对比曲线如图3所示。

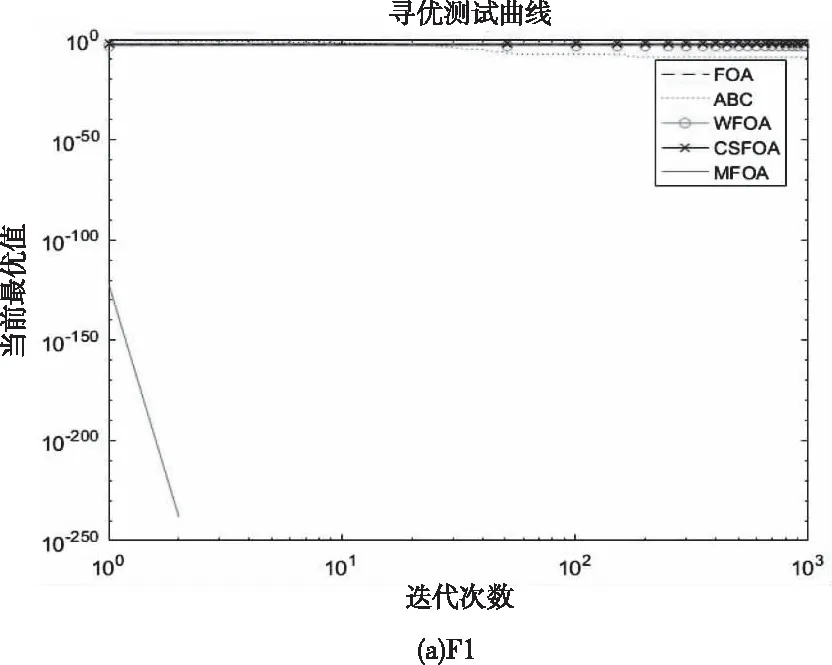
图3 五种算法的寻优测试曲线

由图3可知：在对各测试函数的迭代寻优过程中，MFOA算法与其它算法相比不仅获得较快的收敛速度且易跳出局部最优值。这些结果表明，MFOA算法因为初始种群的多样性和非线性动态变化收敛因子以及柯西变异对最佳果蝇个体位置的优化，能有效地均衡全局寻优和局部寻优性能，增加种群的多样性，具有较强的迭代寻优性能。

4.4 高维多峰函数上的对比分析

全局优化算法普遍存在易陷入局部最优，后期收敛速度变慢、收敛精度低的问题，尤其对于高维、多峰复杂优化问题。将WFOA算法、CSFOA算法和本文算法MFOA在不同多峰测试函数上，对维数依次递增的情况下各算法的优化均值(MEAN)进行实验比较。在不同多峰测试函数条件下，对各算法独立运行20次，结果如表5所示。

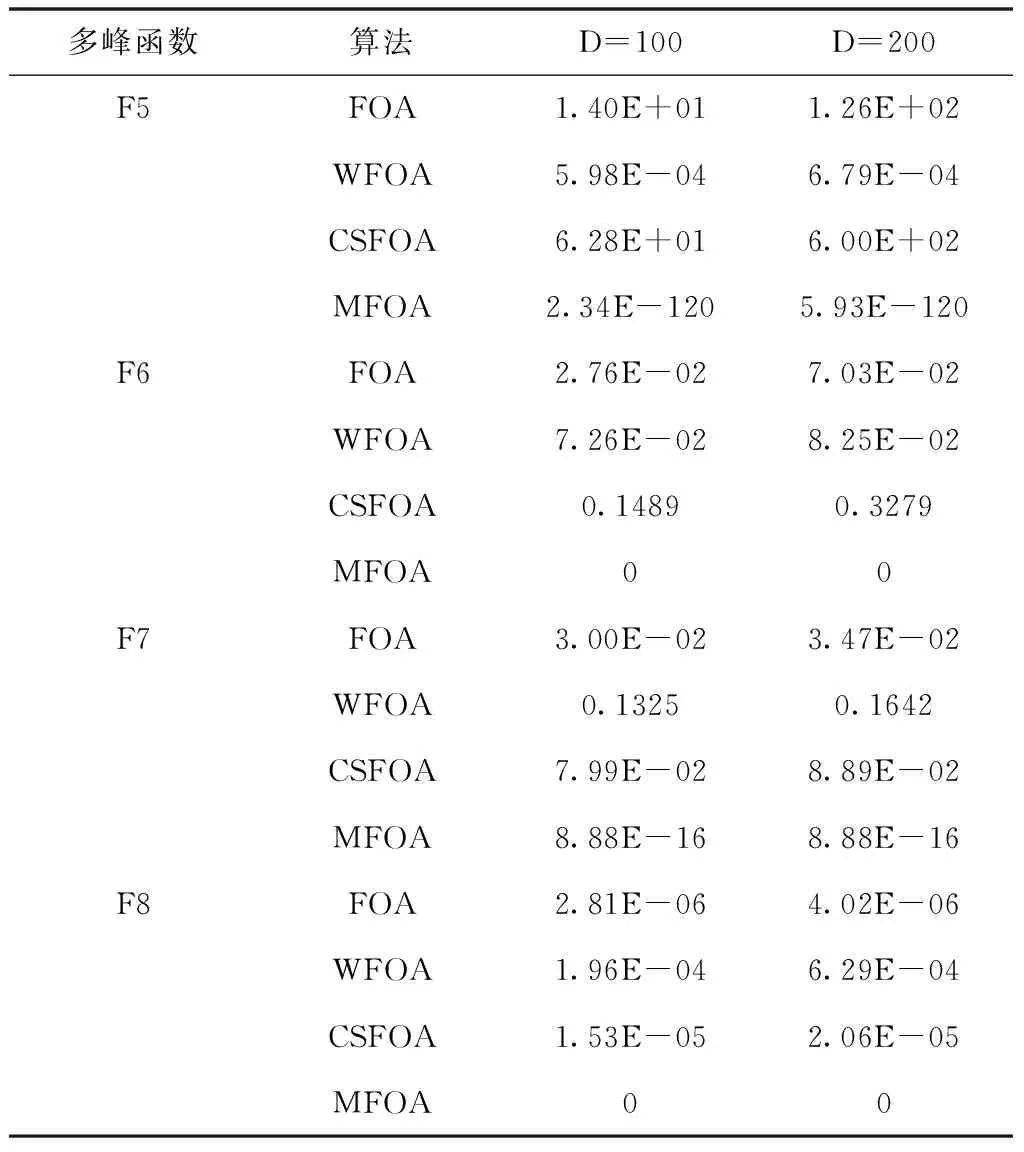
表5 在高维、多峰函数上的优化均值比较

由表5可知，无论维数100还是200，对于多峰测试函数F5和F7，MFOA算法的优化均值显著优于FOA、WFOA和CSFOA算法，并且随着函数维数的增加，MFOA算法的优化均值基本在同一数量级内变化，比较接近最优值，而且对于多峰测试函数F6和F8，随着维数的增加，仍达到理论最优值。这表明MFOA算法对高维的复杂函数仍保持平稳且较高精度的寻优性能。

5 结论

针对FOA收敛速度慢和寻优精度低等不足，提出一种改进算法MFOA，采用Cubic混沌映射初始化果蝇种群以增加种群的多样性；引入非线性动态收敛因子来均衡算法的局部及全局搜索能力；对果蝇最优个体进行柯西变异，增加种群的多样性，以跳出局部最优，提高种群的收敛速度和寻优精度。对8个典型基准测试函数进行仿真，由仿真结果可知，MFOA的测试指标均优于对比算法，这表明该算法在总体性能上具有优势。下一步研究的重点是将MFOA算法应用于实际工程领域中的约束优化问题和多目标优化问题等。