基于STK的北斗三号卫星导航系统AC仿真分析

代建中，冯旭哲，李文屏，邵富杰

(1. 国防科技大学智能科学学院，湖南 长沙 410073；2. 北京跟踪与通信技术研究所，北京 100094)

1 引言

北斗卫星导航系统是我国自主建设、独立运行的卫星导航系统，目前已广泛应用于人类社会的生产生活的各个方面[1]。随着空间科学的快速发展，北斗卫星导航系统服务用户不断扩展，其不仅要为地面用户服务，还要为飞机、平流层飞艇等空间用户服务，因此要考虑卫星系统对空域的覆盖情况。同时空域覆盖具有探测视角高、范围广、时间长的特点，在天基预警、导弹跟踪等方面有着重要军事用途[2]。因此，有必要开展北斗系统空域覆盖性能的相关研究。

空域覆盖不同于传统的地面覆盖，其关注区域扩展至三维空间，覆盖性能也不局限于覆盖率。目前国内外已经对空域覆盖进行了一定的研究：文献[3-5]基于全球定位系统(Global Positioning System， GPS)星座从几何推导的角度对空域覆盖的可见性进行了研究分析；文献[6]在归纳了空域覆盖性能主要因素的基础上，对空域覆盖特性、时域覆盖特性以及两者的联系进行了研究；文献[7]考虑卫星信号波束角和用户最小遮挡角对空域覆盖的影响，对多种全球卫星导航系统(Global Navigation Satellite System， GNSS)方案的空域覆盖性能进行了仿真，但未对覆盖范围内的定位精度进行分析；文献[8-9]分别基于STK(System Tool Kit)对北斗二号系统区域和全球定位的精度衰减因子(Dilution of Precision，DOP)进行了仿真分析，但其仅考虑了对地覆盖的情形。

考虑到文献[3-7]基于GPS系统开展研究，对我国北斗三号全球卫星导航系统空域覆盖性能的研究涉及较少，且仅研究了空间用户的可见星数，未对其定位精度进行分析；而文献[8-9]虽对定位精度进行了一定的研究，但只关注了对地覆盖情形。针对上述问题，本文建立了空域覆盖数学模型，并基于STK对北斗三号卫星导航系统的空域覆盖性能和定位精度进行了仿真分析，研究空间用户随所处空域的变化，其可见星数与定位精度的变化情况。

2 空域覆盖可见性分析

空域覆盖不同于已有的地面覆盖，从卫星的角度，地面覆盖只关注地表的覆盖情况，而空域覆盖要考虑卫星天线可观测的三维区域；从用户的角度，地面用户只需要满足一定的仰角需求即可实现对卫星的可见，而空间用户有一定的轨道高度，能够以一定的负仰角对卫星进行观测。下面分别从卫星和用户的角度进行分析。

2.1 卫星的空域覆盖性分析

卫星的空域覆盖要求观测的空域或空间用户所处的空域位于卫星天线的观测范围之内。卫星天线以一定的辐射角指向地心，观测范围整体呈圆锥形，如图1所示。

图1 单星空域覆盖示意图

在地心地固(Earth Centered Earth Fixed， ECEF)坐标系中，单颗卫星的覆盖情况如图1所示。设卫星S的坐标为(xs，ys，zs)，轨道高度为Hs，卫星在地球表面的切线与卫星和地球球心连线的夹角为β，卫星天线的半辐射角为γ，则恰好与卫星信号辐射范围相切的轨道高度h可表示为[4]

h=(R+Hs)sinγ-R

(1)

对于全球导航卫星系统(Global Navigation Satellite System， GNSS)的卫星，其天线的辐射角一般为32-46°。取地球半径R为平均值6371 km，则可得到h随Hs的关系如图2所示。恰好与卫星信号辐射范围相切的轨道高度h随卫星天线半辐射角γ增大而增大，当空间用户的轨道高度小于h时，卫星的空域覆盖不需要考虑半辐射角的限制；当用户轨道高度大于h时，必须同时考虑半辐射角和可见条件的限制；当卫星天线的半辐射角γ=16°，卫星轨道高度Hs<17000 km时，h为负值，表明此时γ<β，卫星的空域覆盖也要同时考虑半辐射角和可见条件的限制。

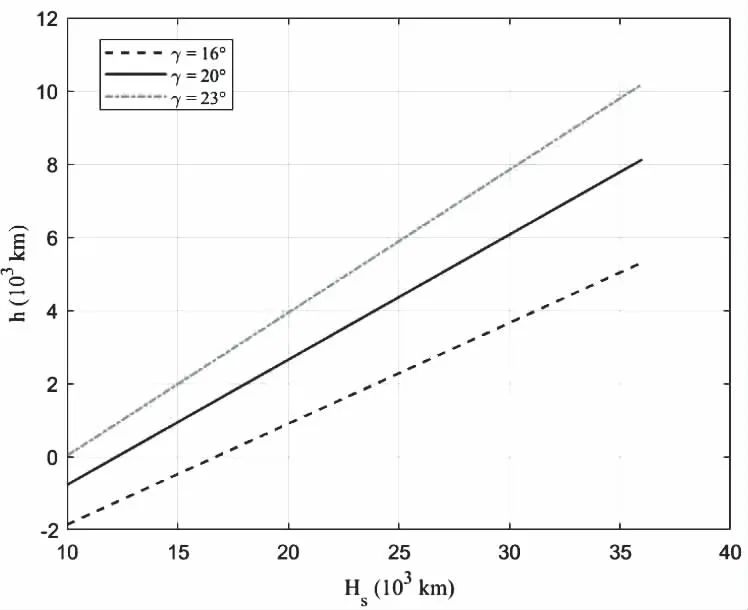
图2 不同卫星天线辐射角下h随Hs的变化情况

2.2 空间用户的观测范围分析

从用户的角度，空域覆盖与地面覆盖也有所不同。空间用户具有一定的轨道高度，地面用户的最小仰角约束不再适用，空间用户不仅能够观测到正仰角范围内的卫星，而且能够以一定的负仰角对卫星进行观测。当空间用户以负仰角进行观测时，要考虑地球及大气层对通信链路的影响。

当空间用户位于大气层内时，引入最小遮挡角σ，即用户在地球表面的切线与临界可见条件下卫星与用户的连线，如图3所示。

图3 空间用户观测范围示意图

在ECEF坐标系中，空间用户U的坐标为(xu，yu，zu)，其轨道高度为Hu，则临界可见条件下，卫星、用户与地球球心之间的夹角θ可表示为

(2)

当空间用户轨道位于大气层外时，由于信号穿过大气层存在衰减、折射等现象，故本文将两次穿过大气层通信链路视为不可见。假设大气层高度为h0，此时卫星、用户与地球球心之间的夹角θ可表示为

(3)

综合上述分析，空间用户对单颗卫星的可见性判断条件为

其中

3 空域覆盖仿真分析

基于式(4)中的可见性判断条件，采用STK软件对北斗三号卫星导航系统空域覆盖性能进行仿真分析。

3.1 仿真场景的搭建

STK是由美国Analytical Graphics公司开发的一款航天系统分析软件，其广泛应用于复杂航空航天任务的仿真和分析[10]。STK强大的计算内核和丰富的模型模板使其在可见性计算、覆盖性计算、通信干扰仿真等方面应用广泛。同时，STK在结果输出方面也设计得当，不仅提供2维、3维可视化窗口，而且提供多种图表、报告的输出类型。

本文仿真对象参考北斗三号卫星星座，北斗三号采取“3GEO+3IGSO+24MEO”的星座构成，卫星与卫星之间具备通信能力，可以在没有地面站支持的情况下自主运行。本文仿真中未考虑星间链路的设置情况，天线波束角取23°。利用STK软件建立上述星座如图4所示，仿真中采用2020.01.01 04：00-2020.01.07 04：00的广播星历，GEO、IGSO和MEO卫星的轨道参数如表1和表2所示。仿真中轨道偏心率取0，近地点角距取0°，MEO卫星构成24/3/1型Walker星座，表2中升交点赤经(Right Ascension of Ascending Node， RAAN)和平近点角均为三个轨道面第一颗卫星对应数值，且轨道面内其余卫星的平近点角依次增加45°。

图4 “3GEO+3IGSO+24MEO”仿真场景

表1 GEO和IGSO卫星仿真参数

表2 MEO卫星仿真参数

3.2 空间用户的可见星数分析

在STK中利用Coverage Definition和Figure of Merit两个模块可以对覆盖问题进行分析，Coverage Definition模块用于对覆盖对象进行定义和覆盖计算，Figure of Merit模块用于输出得到所需指标的品质因数。在进行覆盖分析时，STK不仅可以充分考虑所有对象的可见性约束，实现复杂的数据计算，减小数据误差，而且可以实现覆盖结果的可视化，提供各种分析结果的报告和图表。

考虑到计算机的性能，仿真中经纬度的步长取6°×6°，时间步长取300 s，空间用户轨道高度的步长取1000 km。仿真中固定轨道高度，通过STK软件计算当前经纬度间隔下各个离散点对卫星的可见情况，其统计结果如图5所示。

图5 空间用户的可见星数随轨道高度的变化情况

由图5可知，当空间用户轨道高度位于20000 km以内时，空间用户的可见星数满足定位所需最低要求，即四星可见要求，即该星座可实现20000 km内空域的全覆盖。随着空间用户轨道高度的增加，可见星数呈现出先增后减的趋势。可见星数的增加是由于随着空间用户轨道高度的增加，用户能够观测到负仰角范围内的卫星信号。当轨道高度到达4000 km左右，平均可见星数达到最大，随轨道高度再次增加，平均可见星数开始减少，因为卫星天线的辐射角一定，随用户轨道高度的增加，用户正仰角接收范围内的可见卫星数逐渐减少。

对处于4000 km轨道高度的可见星数进行具体分析，其可见星数随纬度和经度的变化情况分别如图6和图7所示。

图6 当轨道高度为4000km时可见星数与纬度的关系

图7 当轨道高度为4000km时可见星数与经度的关系

由图6和图7可知，可见星数的平均值对纬度变化的敏感性较弱，但可见星数的波动性随纬度降低而增强；当经度发生变化时，仿真结果呈现出如下规律：在10-220°经度范围内，可见卫星的数目明显高于其余范围，这恰好佐证了北斗星座中GEO卫星与IGSO卫星的区域增强作用。

3.3 空域定位精度分析

精度衰减因子是衡量卫星星座定位精度的重要指标，其反映了定位精度受卫星空间几何分布的影响情况[11，12]。针对同一用户，DOP值越大，定位精度越低。精度衰减因子包括位置精度因子(PDOP)、水平精度因子(HDOP)、垂直精度因子(VDOP)和时间精度因子(TDOP)和几何精度因子(GDOP)[4]，其具有如下关系

HDOP2+VDOP2=PDOP2

PDOP2+TDOP2=GDOP2

(5)

GDOP代表由测距误差引起的卫星与接收机之间的距离矢量放大因子，与从接收机至卫星的单位矢量所勾勒的形体体积成反比[13]。仿真中取GDOP作为参考指标对定位精度进行分析，经纬度步长与时间步长保持不变，获取GDOP值随空间用户轨道高度的变化情况，其统计结果如图8所示。

图8 空间用户的GDOP值随轨道高度的变化情况

由图8可知，在4000 km以内随着空间用户轨道高度的增加，GDOP值呈下降的趋势，这是由于随着轨道高度的增加，可见星数随之增加，使得参与定位的卫星满足更优的几何位置关系，从而使GDOP值不断降低。当轨道高度超过4000 km左右，GDOP值随轨道高度增加而减少，同理，该阶段可见星数随轨道高度增加而减少，参与定位卫星的几何位置关系不断变差，导致GDOP值的增大。当轨道高度在8000 km以内，可使得GDOP值均小于3，即北斗三号卫星导航系统对8000 km以内空域均具有较高的定位精度。

对轨道高度4000 km的场景进行具体分析，GDOP值随纬度和经度的变化情况分别如图9和图10所示。

图9 当轨道高度为4000km时GDOP值随纬度的变化情况

由图9和图10可知，GDOP值随经纬度的变化而改变，定位性能也有一定的改变。显然，在纬度由南北极90°向0°的变化过程中，GDOP值稳定性不断弱化，定位精度的稳定性变差，但该轨道高度GDOP值均小于1，具有极优的定位精度。此外，同可见星数的变化规律一致，当经度位于80-140°时，GDOP值较小，定位精度较高，再次验证了北斗星座中GEO卫星与IGSO卫星的区域增强作用。

图10 当轨道高度为4000km时GDOP值随经度的变化情况

4 结论

本文基于STK对北斗三号卫星导航系统的空域覆盖性能和定位精度进行了仿真分析，仿真结果表明：

1)在覆盖性方面，能够实现20000 km以内的全空域覆盖，并满足四星定位基本要求；

2)在定位精度方面，对于8000 km以内空域，北斗三号系统GDOP值均小于3，即对该空域具有较高的定位精度；

3)对轨道高度为4000 km处的空间用户，北斗系统的可见卫星数与GDOP值均达到最优。