基于功率测量的MIMO雷达天线异常检测方法

张晓冬，唐文明，蒋耿明

(复旦大学信息科学与工程学院，上海 200433)

1 引言

近年来，随着毫米波雷达理论的发展和器件的成熟，这项技术逐渐在安防、车载雷达等民用领域发挥重要的作用[1]。毫米波雷达的发射波长为1～10mm，频率分布在30～300GHz。较短的波长使其具备高分辨率的特点和精准的探测能力。根据工作机制，毫米波雷达可分为脉冲体制雷达和连续波体制雷达。其中，调频连续波(FMCW)是后者的代表之一，它通过连续发射调频信号来进行测距、测角和测速等工作。

MIMO技术的应用使毫米波雷达的硬件成本降低，其高分辨率的特点得以施展。MIMO雷达通过增加发送天线TX数构建虚拟的天线阵列，以M根TX天线和N根接收天线RX就可达到与M·N根RX天线的单输入多输出(SIMO)雷达相同角分辨率的效果。其中，天线作为MIMO毫米波雷达系统中的关键模块，其性能优劣直接决定着系统性能，若天线存在异常，则可能导致天线寿命缩短，系统无法正常工作等结果。针对这一问题很多学者提出一些直接或间接检测天线异常的方法：文献[2]实时分析天线通道数据，通过判断数据是否异常来确定通道的工作状态，该方法能够有效定位异常天线，但对于因为电路虚焊等原因导致的天线功率细微损耗所引发的问题则可能出现漏报的情况。

射频功率计是一种常被用于测量雷达信号功率的装置，该功率计可以直接测出功率且频率覆盖广，支持的动态测量范围大[3]，另一种测量功率的方法基于频谱仪，该方法通过脉冲调制信号的频谱来获取平均功率与峰值功率[4]，这些方法虽然提高雷达功率测量精度，但体积和重量都比较大，成本高，且便携性低，故应用场景受限。若在功率测量方法的基础上加以改进提出一种更高效的基于简单电路的方法，则很有可能提高测量的实时性与便携性。

本文在相关研究基础上提出一种基于功率的间接检测天线异常的方法，采用功率芯片TPS259827+CPU实时采集功率信号，结合5/3小波去噪与Hermite包络插值检测MIMO毫米波雷达中天线功率的变化，间接测量MIMO毫米波雷达天线异常。Hermite插值作为一种低阶分段多项式插值方法很好的解决了高阶多项式插值的龙格现象[5]，大大减小了插值误差[6]，稳定性与收敛性都得到了保证[7]。该功率检测模块结构简单，体积小，成本低，不同于传统的分离测量器件，可以集成到雷达系统中，具有较高的应用价值。除了对天线的异常监测外，功率测量有助于为雷达系统的硬件设计提供有价值的参考，如供电系统设计、PCB的板材选择与走线设计等。

2 MIMO毫米波雷达工作机理与功率检测方案

基于FMCW的MIMO毫米波雷达典型的TDM工作机理如图1所示，采用通道分离技术，每根TX天线在其对应的时隙中完成从打开到关闭的操作，令RX天线能分辨出不同TX天线对应的信号，使得虚拟阵列的构造成为可能。

图1 TDM-MIMO毫米波雷达工作机理[8]

由此可知，通过测量系统电源的功率，可以检测雷达设备中天线的运行状况。本文基于系统中天线开启、关闭时出现的功率跳变的现象提出一种可以侦测跳变沿的功率测量方案，其流程主要包括功率信号采集与去噪、跳变沿监测和插值平滑等步骤。

图2 功率测量框图

功率测量框图如图2所示，MIMO毫米波雷达系统由12V电源供电，TPS259827芯片提供电源短路与过压保护等功能，该芯片除输出电源12V电压外，还会监视电源的输入电流。通过GD32F307E单片机读取该信息并转换为功率信号。TDM-MIMO雷达天线在发射和切换时都会引起功率的变化，由此可以监视天线的运作状态。最后，功率信号经信号处理模块滤除噪声的干扰，得到更为精确的天线发射功率测量与异常检测结果。

3 功率信号处理

3.1 信号预处理

系统中功率信号的采集由单片机执行，采集到的电源功率信号不可避免的存在噪声，目前时间序列降噪效果较好的方法有自适应滤波[9]和小波阈值技术[10]等。其中小波变换在时域和频域都有很好的局部化特征，这有助于分析和处理非平稳信号[11]。5/3提升小波简化了传统小波变换的运算过程，在运算资源不充裕的情况下大大提高了算法的运行速度，能够很好的解决因为数据未及时处理引起的数据拥塞问题。

相比于之前基于Mallat算法的快速小波变换，5/3提升小波不依赖于傅里叶变换，从而消除大量复杂的卷积运算，大幅提升了运算速度。

图3 提升小波变换

提升小波变换包括了分解、预测和更新三步骤[12]，其流程如图3所示。数据序列x首先分解为偶数序列和奇数序列子集，偶数序列经预测过程后逼近奇数序列，其与奇数序列差值后得到高频分量H；H经过更新后生成相应的低频分量L，其算法描述如式(1)所示，只需要经过简单的加减和除法运算就可以实现传统小波变换的复杂过程。

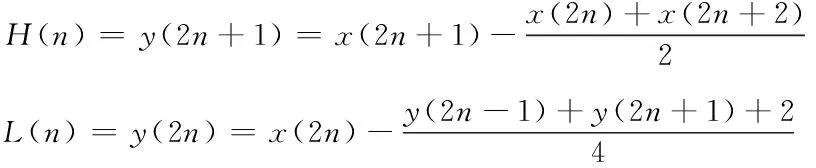
(1)

经过小波变换后，含有噪声的功率信号分解成多尺度下的小波系数。根据一般情况下噪声小波系数幅值小于信号小波系数幅值这一特性，选择合适的阈值对噪声进行消除。由于功率信号中的噪声基本分布在信号的高频部分，因此保留低频分量，只对高频分量进行阈值处理。

阈值T的选取很大程度上取决于噪声的分布情况，这对去噪的效果有着极大的影响。随着分解层数的加深，由深层的低频分量分解出的高频系数中，噪声的成分将变得很小，其对阈值选取参考的贡献也将不大，因此本文只将第一层的小波系数作为考量，根据式(2)计算阈值T，其中σ为小波系数的标准差，n为系数个数。

(2)

常用的两种阈值处理策略是Donoho提出的软阈值和硬阈值函数[13]。信号在软阈值处理前后的幅值将会收缩且难以恢复，这使得测量值产生失真。而硬阈值则会保留大于阈值的小波系数，重构后功率幅值得到很好的保留。因此本文选择硬阈值策略，图4为对信号进行两层小波分解后的阈值去噪流程。

图4 2层小波分解

为了从分解后的小波系数中恢复出噪声消除后的信号，需要执行小波重构，小波重构就是小波逆变换过程，包括反更新、反预测和反合并三步骤[12]，其流程恰为图3的逆过程。经过小波阈值去噪的信号和原始信号的对比如图5所示。

图5 去噪前后功率信号

3.2 信号估计处理

采用Hermite插值法对信号的包络进行软件重采样以提高采样率，然后对插值后的上下包络取平均，能有效提高信号的分辨率与对真实信号的估计。

3.2.1 Hermite包络插值

本文采用的两点三次Hermite样条插值在传统的Hermite插值[14]基础上做了简化，提高了运算效率。其算法如下：对函数y=f(x)在节点xi和xi+1的数据进行插值，在给定两个插值点的函数值y(x)和一阶导函数g(x)的条件下，即可计算出插值函数。

(3)

其中αk(x)、βk(x)均为插值基函数。

从图5(b)可以看出经过去噪后的信号仍然存在较大的抖动，若对此信号直接插值，则结果必然会导致最终的读数仍存在较大幅度的抖动。为了平滑数据抖动，本文首先取信号的上下峰值点，再基于这些点进行插值，得到插值后的上下包络。最后，将插值后的上下包络平均作为结果。

图6 包络插值

在进行Hermite插值时，数据的一阶导信息无法预知，本文采用简单的三点差分法来近似包络E(n)插值点处的一阶导数值。

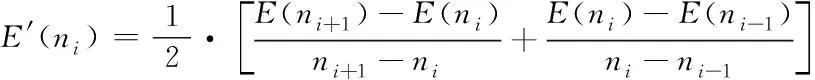
(4)

插值后，数据点的增加丰富了功率信号的细节信息。接着将两条包络曲线作平均，得到如图7所示平滑后数据的结果。

图7 上下包络平均

可以看到，数据得到了极大的平滑，曲线过渡自然，波动也不再剧烈。但与此同时，跳变沿处的数据也被同步平滑，此处的曲线较原信号更加平坦，产生失真。针对这一问题，本文通过侦测跳边沿来避免信号的失真。

3.3 功率跳变侦测

为了避免在平滑信号波动时，功率跳变沿被同时平滑，对输入的信号进行跳变沿检测，若存在则对此段数据作特殊处理。以下的方法原理简单，计算复杂度低，但能有效的定位跳变沿。

3.3.1 数值变化趋势计算

如果对插值后数据量大幅增加的信号进行处理，则会加重硬件的计算负担，因此本文在插值前即开始检测功率的跳变。

观测到图5(b)在跳变沿处的数据有2个特点：功率幅度变化最大，跳变时间极短。考虑到去噪后残留的噪声幅值一般都是小于功率跳变幅度，因此计算出一段数据不同时间段内的功率变化值，若该段数据中存在跳变沿则必然存在于变化值最大所对应的那个时间段内。

在未做任何平滑的情况下利用简单的滑动窗口平均法可以稀释数据量，减少残留噪声的影响。

(5)

其中，k为滑动窗口的大小。接着，对数据采用式(6)所示的前向差分，计算出信号的变化差值随时间的变化情况。其中，d为差分间隔。

delta(m) =w(m+d)-w(m)m=1，2，…

(6)

将以上的算法应用于存在两个跳变沿的图5(b)信号中，结果如图8所示。该图很明显的存在两个尖峰，且幅度远大于其它峰值，不难推断，位于左边的尖峰对应着功率的上升沿，而右边的则对应下降沿。由此可以根据峰值的大小判断数据中是否存在跳变。

图8 数据变化趋势

3.3.2 跳变点定位

由于经过滑动窗口平均，图8中的每一个点都对应着信号中的一段区间，为了准确定位功率的跳变点，采用最小二乘估计法(LSE)对位置进行估计。

以图8为例，若左边尖峰所包含的数据点为Xi，定义待估参数为XOPT，算法描述如下

(7)

求解上式可得

(8)

由于信号的数据点间隔相同，上式可化简为

(9)

根据式(9)所求得的XOPT即为功率的跳变点，结合确定跳边沿长度的先验条件，确定跳变区间。

图9 定位功率跳变沿分段处理

观察到上升沿和下降沿处的信号并不存在明显的抖动，对处在跳变区间的数据进行单一插值，而对其它数据就采用包络插值平均处理，分段处理后的结果如上图所示。

4 系统测试与实验结果

本文的测试平台为自主研发的雷达信号处理板卡，该板卡载有四片包含3发4收天线的AWR1243芯片，可以实现雷达信号的定时发送和接收，配置芯片调频连续波参数等功能。除此之外，板上集成了GD32F307E单片机与功率测量芯片，单片机通过ADC接口读取系统的电源功率。

图10 MIMO雷达天线评估实验装置图

表1 MIMO雷达天线评估实验参数表

配置雷达信号处理板卡，开启所有天线，表1为实验的设置参数。天线以时分复用的方式轮询发射，采集到的电源功率信号如图11(a)所示。应用本文的算法对信号进行处理，得到的最终结果如图11(b)所示。从实验结果看出，在12根发射天线中，有3根天线的发射功率小于其它天线(按从左至右的顺序记为天线7、8、9)，相比于原始功率信号，在经过算法处理后，该异常现象更加明显。经计算验证，算法处理前后，3根异常天线与其它正常天线发射时的功率信号方差比如表2所示，处理后的方差比分别下降了7.57%、9.50%和8.60%，表明本文的算法有效地放大了数据中异常天线与正常天线之间的差异性。

图11 雷达开启前后的系统电源功率

表2 算法处理前后异常天线与正常天线的功率信号方差比(平均值)

5 结论

本文提出的基于功率测量的MIMO毫米波雷达天线异常检测法，利用单片机+功率芯片读取系统电源功率，并对读取到的信号采用如下方案：

1) 预处理：利用5/3提升小波阈值法对信号进行去噪；

2) 包络处理：对信号取上下包络并求均值以平滑数据的波动；

3) 功率跳变沿侦测：利用滑窗差分评估数据的变化趋势以判断数据段中是否存在跳变沿，并结合最小二乘法精确定位跳变点。

能有效测量出MIMO毫米波雷达天线功率实时变化值，可以直观地获取各天线发射所消耗的功率，天线开启、关闭的时间和天线间的均匀性等信息，间接对各天线性能进行有效评估，具有方法灵活、结构简单的特点。实验结果表明，本文的测量方法在对天线异常检测的场景中具有良好的实际应用效果，具有推广作用，可以应用于其它的如供电模块检测、过流保护等系统。