谐波齿轮系统的快慢振荡机制研究1)

韩修静 黄启旭 丁牧川 毕勤胜

(江苏大学土木工程与力学学院,江苏镇江 212013)

引言

谐波齿轮减速器是为了适应航天器的发展而发明的一种新型传动装置.由于它具有传动比大、结构紧凑、噪声低、传动效率高、精度高等诸多优点,因而被广泛应用于航空航天、工业仿生以及军事等领域[1-3].由于谐波齿轮其自身的结构特点,系统受到了诸多非线性因素的作用,例如扭转刚度、摩擦、运动误差、传动迟滞等[4-6],其作用载荷具有多源和多路径的特征[7-8].这使得系统产生了复杂的振荡响应,严重地影响了系统的正常工作[9-10].围绕谐波齿轮系统的动力学问题,如动力学建模[11-13]、非线性因素的刻画与表达[14-16]、动力学特性分析[17-19]、振动与控制[20-22]等,学者们开展了深入研究,取得了丰富的研究成果.

然而,关于谐波齿轮系统的动力学问题,相关研究主要集中在同一时间尺度下的情形;对于不同尺度耦合作用下的快慢动力学,相关研究鲜有报道.注意到,在谐波齿轮减速器系统中,输入端(含波发生器)的转动惯量通常要比负载端(含柔轮或刚轮) 的转动惯量低2～3 个量级[23-24].因此,谐波齿轮系统是一个典型的快慢系统,它涉及快慢两种振荡尺度之间的耦合作用,而这会进一步导致快慢振荡的产生[25].事实上,在谐波齿轮减速器系统中,可以经常观测到快慢振荡现象.例如,Taghirad 和Bélanger[26-27]研究发现,低转速下的谐波齿轮系统能够产生明显的快慢振荡.随后,发现了类似的快慢振荡,指出这种振荡可能与扭矩波动有关.特别地,在由谐波齿轮驱动的诸如机械手、机械臂等装置中,可以观测到类似的快慢振荡[28-30].然而,由于谐波齿轮系统的复杂性,关于快慢振荡的研究,主要集中在现象报道上,而很少涉及动力学机理方面的研究.

本文考虑涉及扭转刚度非线性因素的谐波齿轮系统,旨在揭示系统中的快慢振荡及其动力学机制.当扰动力矩的频率远小于系统的固有频率时,即当扰动力矩的频率和系统的固有频率之间存在量级差异时,可以观测到快慢振荡如图1 所示.特别地,这种快慢振荡其形式与之前的有关报道[31]非常相似.然而,研究表明,这里的快慢振荡与平衡点曲线在局部小范围内发生的急剧量变有关,其特征是平衡点在局部小范围内可以在正坐标值与负坐标值之间快速转迁.这是一种不同于以往所报道的新型动力学机制.

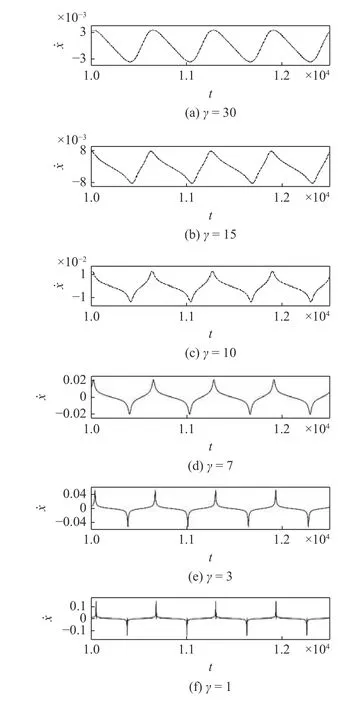
图1 谐波齿轮系统从(a)～(c)常规振荡模式向(d)～(f)快慢振荡模式转迁Fig.1 A transition of the harmonic gear system from (a)～(c) normal oscillation modes to (d)～(f) fast-slow oscillation modes

1 模型和快慢振荡

考虑刚轮固定,柔轮作为输出轮时的谐波齿轮传动系统.根据谐波传动原理,可得系统的简化模型[11],如图2 所示.在图2 中,Ji和Jo分别是输入端和负载端的转动惯量,θi和 θo分别是电机输入端角位移和负载端输出角位移,Tim是输入轴的静态平均力矩,Tom是谐波齿轮柔轮输出力矩,N是减速比,K(θ) 是非线性扭转刚度,Ceq是系统的等效阻尼系数.

图2 谐波齿轮系统的简化模型[11]Fig.2 Simplified model of the harmonic gear system[11]

根据谐波齿轮传动系统的力学关系,可得如下的运动微分方程

谐波齿轮传动系统中的摩擦行为十分复杂,为了便于分析,这里采用文献[20]给出的等效阻尼系数Ceq来近似刻画系统中的摩擦因素,即

非线性刚度K(θ) 是系统重要的非线性因素,其贡献不仅有齿轮啮合部分,还包括柔性轴承部分.本文采用文献[6]给出的非线性刚度形式,其兼具了上述两个部分对扭转刚度的影响,即

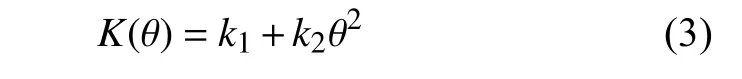
其中,k1和k2是扭转刚度系数,θ=θo-θi/N是相对扭转角(θi,θo和N的含义同前).

在系统(1)中,f(θ) 是谐波齿轮单向转动时的间隙空程[20],即

其中,θ 的含义同前,φ 是尺侧间隙空程.

本文假定谐波齿轮柔轮输出力矩Tom受到周期慢扰动的影响,可以表示为Tom=Tfs+Tamsin(ωt) 的形式[25],其中Tfs=Tim,0 ＜ω ≪1 .不妨记于是,原四维非线性系统(1)可以简化成二维非线性系统(5)

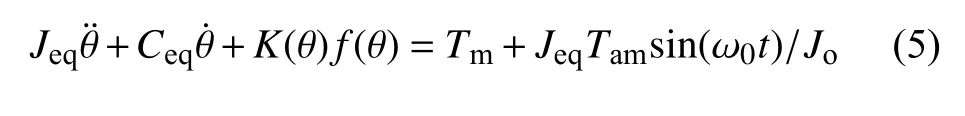
将方程(5)进行无量纲化,可得

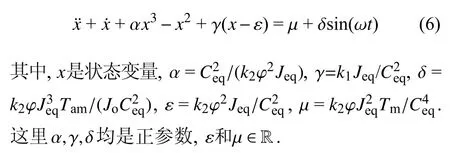
取定系统参数Tm=10 N·m,Tam=15 N·m[25],其他参数由表1[11]给出.此时,系统(6)的无量纲参数分别是 α=16,γ=30,ε=0.71,µ=0.07,δ=15 .数值模拟表明,当扰动力矩缓慢地(例如,ω=0.01)周期变化时,系统产生了普通的周期响应,见图1(a).然而,如图1 所示,随着参数 γ 的不断减小,系统逐渐演化为快慢振荡,其特征是在时间序列中周期地出现了“脉冲”形的大振幅振荡(例如,见图1(f)).从形式上来看,这种快慢振荡与文献[31]所报道的振荡模式非常相似.将在本文的第4 部分揭示其产生的动力学机制.

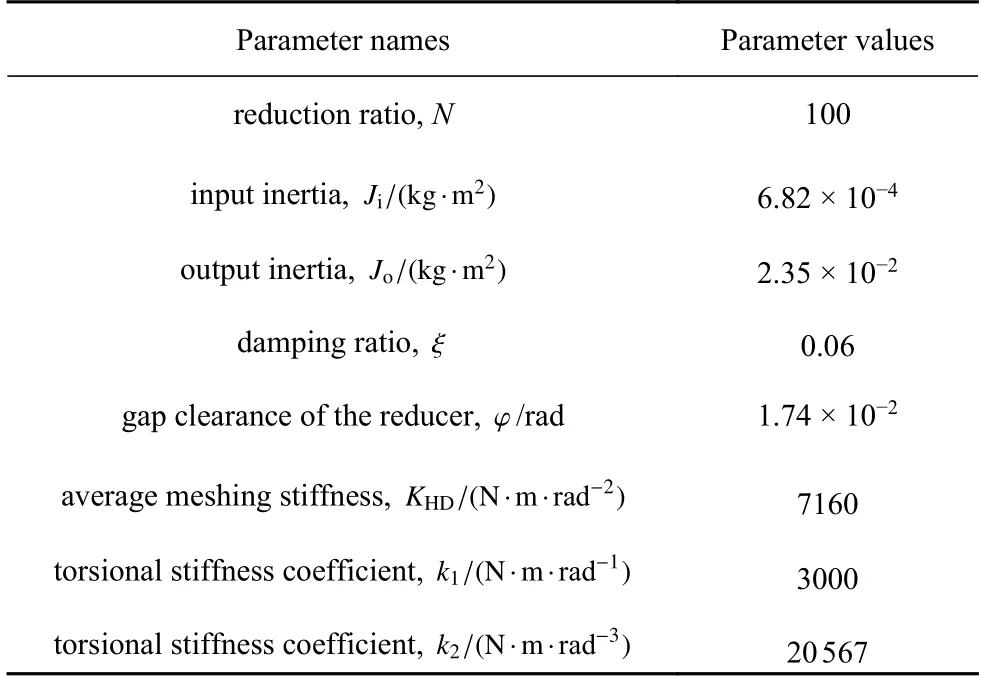
表1 系统参数[11]Table 1 System parameters[11]

2 快慢分析法

为了揭示图1 中的快慢振荡的动力学机理,本部分对快慢系统的定性分析方法,即快慢分析法[32],作简要论述.

一般地,快慢振荡可由以下形式的快慢系统加以描述

其中,ε ≪1 是快慢时间尺度的比率,x∈Rm是快变量,y∈Rn是慢变量.快慢振荡是一种特殊的振荡模式,需采用特殊的分析方法加以研究.Rinzel[32]提出的快慢分析法是揭示快慢振荡动力学机理的经典方法,其基本思想是将快子系统(7)与慢子系统(8)分开讨论.快子系统的动力学行为由慢变量加以调控:快子系统可以处于不同的运动态,这由慢变量的值决定.将快慢系统的相图与快子系统的分岔图(其中,慢变量视为快子系统的分岔参数)进行叠加,进而可以解释快慢振荡的动力学机理.

3 快子系统的动力学特性

注意到本文关注的情形是扰动激励缓慢地变化,且其频率远小于系统的固有频率.因此,根据文献[33],可将系统(6)视为一个快慢系统:慢变量是sin(ωt),快子系统是

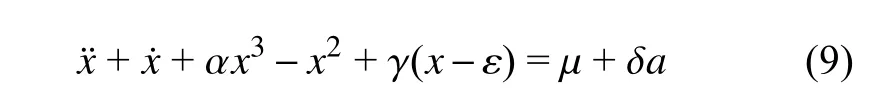
其中a=sin(ωt) 是控制参数.为了便于分析,本文将α,µ,ε,δ 的取值固定(与图1 中的取值相同),仅将γ和a视为系统参数.

显然,快子系统(9)的平衡点可以写成E=(x,0),其中x由方程

的实根决定.方程(10)的根的判别式为

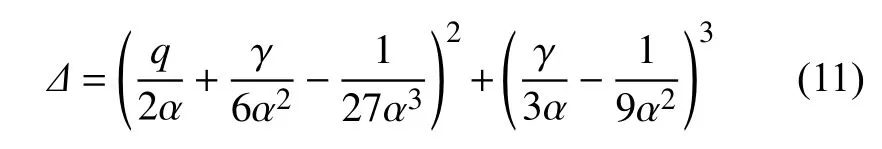
其中q=-(γε+µ+δa) .显然,系统其他参数固定,当,即当时,判别式 Δ ＞0 恒成立,系统(9)仅存在一个平衡点E.进一步的分析表明:平衡点E是稳定的焦点.

基于上述分析,下面探讨平衡点E的动力学特性.图3(a)给出了不同参数值 γ 下的平衡点曲线.可以发现,随着 γ 的数值不断减小,原先较为平缓的平衡点曲线发生了连续的弯折变形.特别地,在参数a=0附近,平衡点曲线变得陡峭,其特征是平衡点坐标可在正值与负值之间迅速转迁;其陡峭程度随着γ的数值递减而逐渐加剧.图3(b)给出了不同参数值γ下的平衡点曲线的变化率,这进一步证实了系统在参数a=0 附近发生的急剧变化.

图3 平衡点E 的动力学特性Fig.3 Dynamical characteristic of the equilibrium E

4 快慢振荡的动力学机理

前一部分揭示了快子系统在参数a=0 附近的动力学特性.在此基础上,本部分探讨快慢振荡的动力学机制.

如前所述,当 γ 不断减小时(可通过改变扭转刚度系数来实现),平衡点曲线将在a=0 附近发生急剧量变.如图4 所示,这种急剧量变的动力学特性,形成了一个狭小的“激发态区域”(spiking area).当参数取在“激发态区域”时,系统将发生急剧转迁.在“激发态区域”的左右两侧,系统的动力学特性较为温和,由此形成了两个“沉寂态区域(quiescent area)”.

图4 (示意图)系统的激发态区域(黄色)和沉寂态区域(灰色)Fig.4 (Illustrative diagram) Spiking area (yellow) and quiescent area (gray)

当慢变量 s in(ωt) 被接入系统时,s in(ωt) 周期地缓慢穿越“激发态区域”和“沉寂态区域”.这导致系统在“快速转迁”和“慢速演化”中不断交替,例如见图5(a1),图5(a2),进而形成了所谓的快慢振荡.特别地,如图3 所示,当 γ 不断减小时,“激发态区域”中的量变行为越来越剧烈.这导致系统的快慢振荡特征愈发显著,例如见图1(d)～图1(f).

另一方面,当 γ 较大时(例如 γ=30),平衡点曲线没有形成“激发态区域”.此时,系统随着平衡点曲线一直“缓慢”地演化,而没有“快速转迁”现象的发生,例如可见图5 (b1).因此此时无法产生快慢振荡,只形成了较为常规的振荡模式,例如见图5 (b2).

注意到在本文的研究中,所涉及的两个沉寂态区域中的吸引子均是平衡点,因此以图5(a1)和图5(a2)为代表的快慢振荡,其本质上属于“点-点”型.需要指出的是,“点-点”型快慢振荡是一种较为常见的振荡模式.在以往的研究中,“点-点”型快慢振荡通常与折(fold)分岔[34]和亚临界Hopf 分岔[35]有关.此外,延迟分岔(delayed bifurcations)[36]等因素也可以诱发“点-点”型快慢振荡.然而,本文中的“点-点”型快慢振荡不是由具体的某种分岔所引起的,而是由平衡点曲线的急剧量变所诱发.

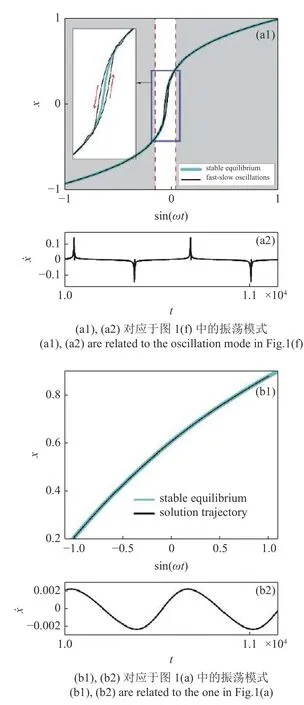
图5 典型振荡行为的动力学分析Fig.5 Dynamical analysis of the typical oscillation modes

最后指出,脉冲式爆炸[37]和吸引子的极速逃逸[38]等因素是已知的可以诱发快慢振荡的其他急剧量变行为.然而,脉冲式爆炸的特征是,在平衡点曲线上形成了“脉冲”型的尖峰;而吸引子的极速逃逸的特征是,平衡点在某点附近迅速趋于无穷大.这些均与本文报道的急剧量变行为不同.综上所述,本文揭示的快慢振荡的诱发机制,是未曾报道过的新型动力学机制.

5 结论

快慢振荡普遍存在于谐波齿轮传动系统;探讨快慢振荡的动力学机理问题具有重要意义.本文研究涉及扭转刚度非线性因素的谐波齿轮传动系统的快慢动力学,揭示诱发快慢振荡的新机制.研究表明,当扭转刚度系数不断减小时,平衡点曲线可以产生不同于以往的急剧量变,即在某局部小范围内,平衡点可在正、负坐标值之间快速转迁.这直接形成具有不同动力学特性的激发态区域和沉寂态区域.在慢变量的调控下,系统在激发态与沉寂态之间相互转迁,进而产生快慢振荡.本文的研究丰富快慢振荡的诱发机制,为实际谐波齿轮传动系统中的快慢动力学机理与控制研究提供参考.