台风过境下大型单桩式海上风机结构动力特性研究1)

秦梦飞 施 伟,†,2) 柴 威 付 兴 李 昕

* (大连理工大学建设工程学部,辽宁大连 116024)

† (大连理工大学海岸与近海工程国家重点实验室,辽宁大连 116024)

** (武汉理工大学船海与能源动力工程学院,武汉 430063)

引言

海上风电作为最具商业化前景的一种可再生能源,近年来得到世界各国的高度重视,呈现出跨越式发展.2020 年我国新增海上风电装机规模306 万千瓦,占据全球新增容量的50%[1].我国海岸线长度超过18 000 km,可开发利用的风能资源丰富,且我国经济发达城市集中在沿海地区,发展海上风电可就近供给,缓解能源供应压力并助力碳中和.然而,我国东南沿海处于台风易发区域,以广东为例,近60 年的统计资料表明对广东省沿海有影响的年均台风次数达到了5 次,其中超强台风占到了年均总数的49%[2].台风频繁经过极大地影响了海上风电结构的安全性:一方面,大型风机的塔筒与叶片属于高柔性结构,在台风作用下易产生变形与振动,具有极强的风致敏感性;另一方面,台风会引起巨大的台风浪,对海上风机基础造成灾害[3].目前,全球并网的海上风机,80% 采用单桩式基础.因此,开展台风与台风浪联合作用下大型单桩海上风机响应研究具有重要的工程意义.

对台风过境期间风场的实测数据表明,台风与常态大风具有不同的湍流特性[4-7].Li等[8]依据台风黑格比的实测数据,拟合出台风不同区域的风谱,结果表明相对于常规风场,台风区归一化风谱的谱峰频率向高频转移.美国国家可再生能源实验室(NREL)[9]比较了风机分析标准中所用的多种湍流谱模型,发现即使平均风速与湍流度相同,采用不同风谱模型将导致结构响应产生较大差异.韩然等[10]学者将台风风场划分为涡旋区与大风区,比较了中国抗风设计指南中推荐的Simiu 谱与实测风谱下风力机动力响应结果,结果显示在台风大风区实测风场与规范推荐谱得到的风场脉动特性类似,但涡旋区差异则较大.Wang等[11]将台风过境全程分为五个区域,对过境全程风力机载荷效应进行了数值模拟,结果表明台风效应极大地增加了风力机的风载荷极值,且风载荷的增加呈现出非线性特性.李琪等[12]使用有限元方法分析了导管架与单桩基础在台风经过时的结构响应,得出了导管架基础风力机动力响应较小的结论.Kim[13]使用气象海浪耦合模式University of Miami Coupled Model (UMCM)模拟台风路径,得到风浪耦合下导管架基础风力机动力响应,并在模拟台风场时使用了IEC 规范中的Kaimal 谱.朱彬彬等[14]建立了台风作用下运营期内海上风机基础结构失效模式及评价指标.芦直跃等[15]通过物理模型实验,研究了台风对海上风电单桩基础累积变形的影响,结果指出可采用叠加法计算存在台风时单桩基础的累积转角.

在风电基础结构动力特性方面,姜贞强等[16]使用ABAQUS 有限元软件,对单桩基础在我国黄海50 年一遇的极端载荷作用下的动力响应进行了研究,结果表明增大桩径及壁厚可有效增大单桩刚度,减小泥面线处动力响应.孙肖菲等[17]使用有限元对大直径单桩基础固有频率影响因素进行了研究,研究结果表明基于梁单元及非线性弹簧单元体系计算得出的一二阶固有频率明显小于实体单元所得结果.刘晨晨等[18]使用ABAQUS 研究了地震与波浪共同作用下桩的动力响应,结果指出相较于地震载荷,波浪载荷影响较小.Bergua等[19]基于国际能源署OC6 项目,采用不同数值模拟软件,对10 MW级大型单桩结构的高精度桩土作用模型进行了对比验证.Bachynski等[20]在SIMA 中使用宏元素考虑桩土相互作用,比较了等效风暴法中不同风暴面对结构响应的影响,其结果表明风暴中最大响应不一定出现在有义波高最大的区域.

国内外针对台风对海上风电结构的影响,已做了大量的研究工作.然而,上述研究仅计入了台风影响,忽略了台风浪的作用,或在模拟风速场时使用了规范推荐谱.本文结合台风期间实测风谱,开展风浪联合作用下10 MW 级大型单桩海上风机动力响应研究,重点关注整个台风过程中,不同台风阶段海上风机的动力响应特性.研究发现,在台风经过的不同阶段,单桩海上风机结构表现出不同的动力特性.

1 计算理论

1.1 风载荷计算理论

风机叶片载荷计算多采用叶素动量理论.叶素动量理论[21]结合了叶素理论与动量理论,将叶片沿径向分成多段,将每段视为独立的二维翼型单元[22],假设各单元之间流场互不影响,每个单元中心处相对风速与雷诺数分别为

其中 ρair为空气密度,c为叶片 截面弦长,νair为空 气黏度,uwind为来流风速,ufoil为叶素单元速度,ur为相对速度,Vrx及Vry为相对速度在叶片坐标系下的分量.

基于雷诺数以及相对风速攻角,在翼形库中选取升力系数CL、阻力系数CD、力矩系数CM,可计算出各单元所受风载荷

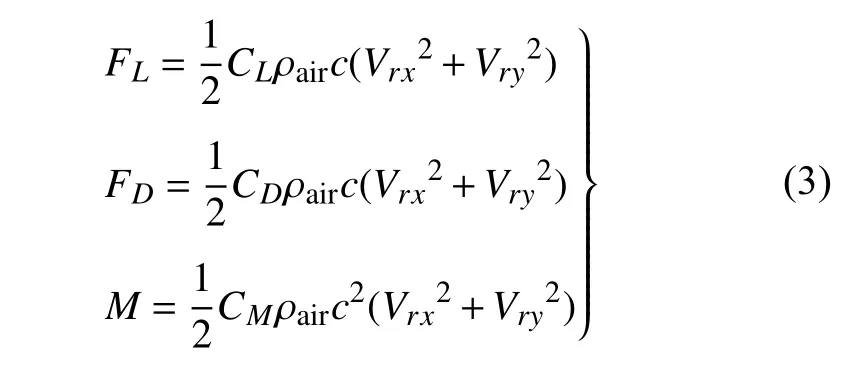
沿径向积分即可得到叶片所受气动载荷.

水面上的塔筒及桩基础同样受风载荷作用,单位长度风力为

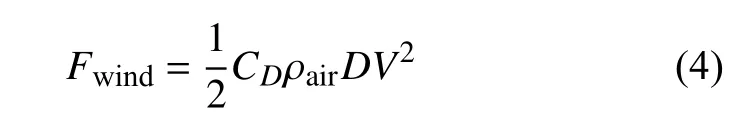
对于圆柱形结构,阻力系数CD取1.2,D为结构外径,V为相对风速大小.

1.2 波浪载荷计算理论

本文使用Morison 方程[23]计算桩基础所受波浪载荷.假定桩基础的存在不影响波浪运动,则桩基所受波浪力由惯性力及速度力构成

式中,ρ 为海水密度,取1 025 kg/m3,Cm和CD分别为无量纲质量力系数与拖曳力系数.ar为流体质点相对桩基础的加速度,ur为流体质点与结构的相对速度

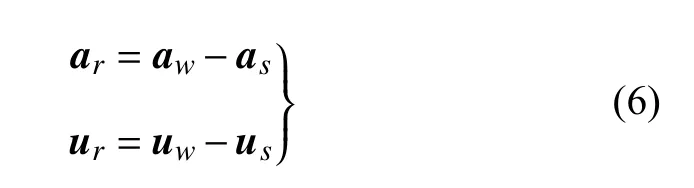
式中,下标w与s分别代表流体质点与结构点,流体质点速度与加速度由二阶斯托克斯波浪理论计算得到.不规则波的一阶波面升高及一阶速度势根据波浪谱由线性波叠加得到

式中,η与 ϕ 分别表示波面升高与速度势,上标代表摄动展开阶数,A为组成波幅,ε为组成波随机相位.不规则波中的二阶波面升高及二阶速度势在一阶波面升高及一阶速度势的约束下得到,将一阶速度势代入二阶自由表面条件中,求解拉普拉斯方程,可得二阶速度势

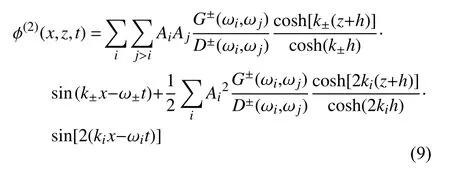
式中,上标 ± 表示分别取+和 -后求和,G与D分别为

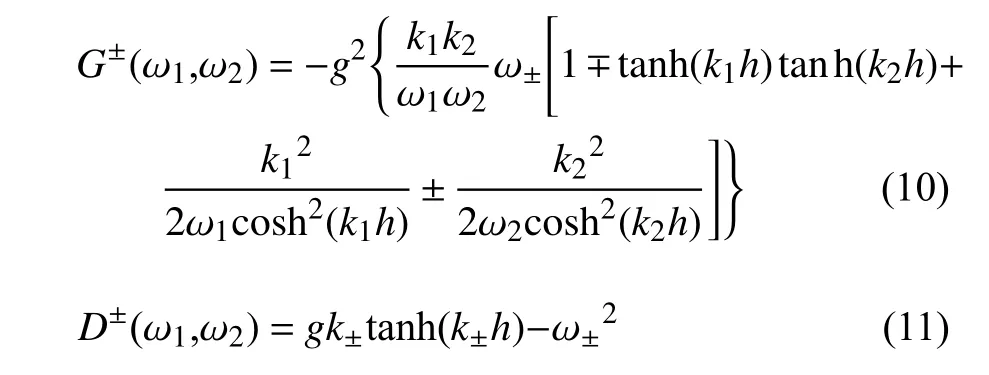
进一步可求出二阶波面升高,将一阶结果与二阶结果相加得到总波面升高及速度势,进而由速度势得到流体质点速度与加速度.

为保证二阶波浪的有效性,二阶规则波需满足3 点:(1)二阶项远小于一阶项;(2)波谷不会触底;(3)波浪不发生破碎.对于二阶不规则波浪,Hu 和Zhao[24]在大量数值模拟的基础上,提出当Hs/Lz小于0.08时,可认为二阶不规则波是有效的.其中Hs为有效波高,Lz为零交叉频率对应的波长.本文据此准则选择波谱的截止频率,对最恶劣的工况FEWS 阶段,当截止频率为3 rad/s 时,Hs/Lz约为0.072,此时忽略了约0.13%的总能量.

1.3 台风风场模拟

湍流风场可以看作不同时空尺度的漩涡叠加,湍流谱描述了风场中能量的分布,根据柯尔莫哥洛夫假设,惯性子区内的风谱为[8]

式中,au为常数,取0.5;K为波数;ε为能量传输率,在表面层中为

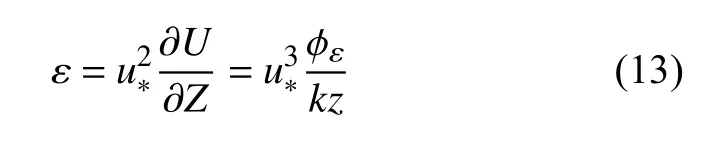
其中,k为卡尔曼常数,u*为摩擦速度,U为平均速度,ϕε是风切变的无量纲莫宁-奥布霍夫函数,在中性大气条件下取1.

结合式(12)与式(13),湍流风谱为

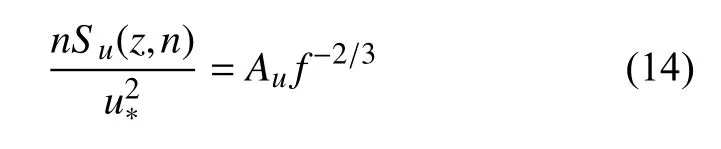
式中,Au为无量纲常数,通常等于0.27,n为频率,f为经高度z与平均速度u无量纲化后的频率,f=nz/u.现存的风谱模型大都基于式(14) 得到,结合Wang等[11]提出的方法,可将台风风场分为五个区域:台风外围涡旋前缘FOVS (front outer vortex stage)、前眼壁强风区FEWS (front eye wall stage)、台风眼TES (typhoon eye stage)、后眼壁强风BEWS(back eye wall stage)、外围涡旋后缘(back outer vortex stage).将台风经过各阶段的纵向风功率谱考虑如式(15),其中对风速平缓的台风眼区域,使用了IEC 规范中推荐的Kaimal 谱,其余区域风谱则使用Li等[8]基于2008 年14 号台风黑格比在南海的实测数据提出的湍流谱

式中,σ 为湍流风速标准差,Vhub为轮毂处风速,L为紊流尺度,现有规范中的风谱模型忽略了纵向风谱与横向风谱的相关性,纵向风谱与横向风谱各自基于实测数据由式(14)拟合得到[25-28].冯·卡门基于各向同性假设,提出横向风谱与纵向风谱应有以下关系

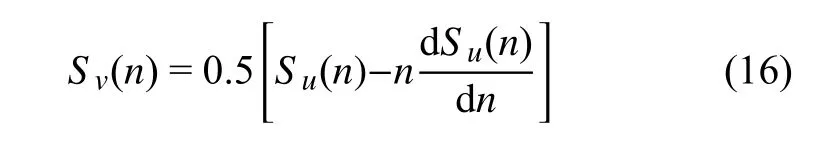
式中,系数0.5 是由各向同性假设所决定的,实际台风过程中湍流风场并非各向同性的,因此,需对式(16)进行修改.Tao等[29]提出可用参数km代替系数0.5 以考虑湍流场的各向异性

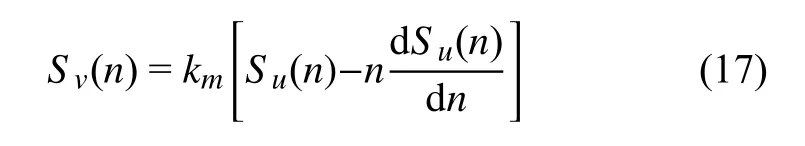
湍流风速标准差与湍流谱有如下关系

式中,下标i=u,v表示纵向、横向.将式(14)及式(18)代入式(17),可得

对台风风场的大量实测数据表明σv/σu在0.7至0.8 之间[30],本文中取 σv/σu=0.75,即km=0.28 .

湍流风模拟主要采用线性滤波法(AR 法)或谐波叠加法.线性滤波法[31]法将零均值随机序列通过滤波器变换成具有指定频谱特征的随机过程.谐波叠加法[30,32-33]则将风速视为一系列正弦波的叠加,理论简易且模拟结果精度较高,但较为耗时.由于线性滤波法算法繁琐,因此,本文采用谐波叠加法在Matlab 软件中模拟得到台风各阶段风场.模拟过程中采用Davenport 公式考虑各点风速之间的相关性,如式(20)所示,模拟过程中横向衰减系数Cy为7,垂向衰减系数Cz为10,u为平均风速,i,j表示空间中任意两点.图1 所示为模拟得到的前眼壁强风(FEWS)阶段轮毂处风速时程图及由风速时程曲线得到的拟合谱与目标谱的对比,FEWS 阶段轮毂处样本平均风速49.05 m/s,轮毂处标准差5.985,标准差与目标值相差仅3%,可见模拟结果较为准确

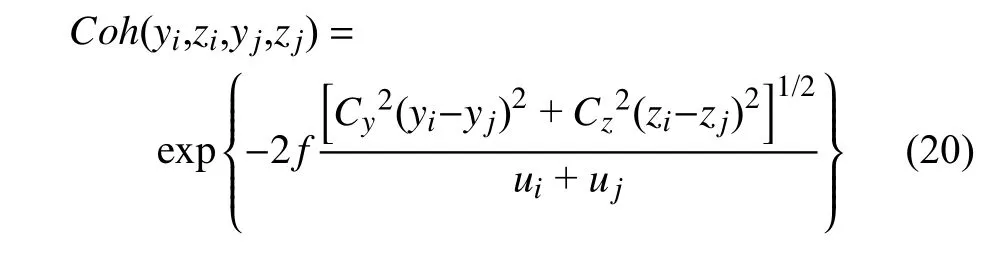
图1 FEWS 阶段轮毂处风速曲线及谱对比Fig.1 Wind speed at hub height and the comparison between target spectrum and fitted spectrum

1.4 台风浪模拟

海浪谱描述了海浪内部能量随频率的分布,目前海洋工程中常使用PM 谱与JONSWAP 谱模拟随机海浪[34].PM 谱由无限风距测得,用于描述充分发展的海浪,JONSWAP 谱是在有限风距情况下测得的,适用于不同成长阶段的海浪.现有研究表明,JONSWAP 谱能够较好的描述台风浪,本文使用Young[35]提出的经验公式由十米高度处平均风速计算有义波高,结合JONSWAP 谱中谱峰频率及有义波高的关系计算谱峰频率

式中,Hs为有义波高,U10为十米高度处平均风速,g为重力加速度,E为波浪能量,可由有义波高得到,ε为无因次波浪能量,υ为无因次谱峰频率,fp为谱峰频率.JONSWAP 谱形式是在深水区域测得,在浅水区域,受海底影响,波谱产生变形.为考虑浅水效应,对得到的J 谱进行修正.将原有J 谱乘以一个修正因子Φ,该因子与水深h及波数k有关,如式(24)所示

波数k可借助色散关系由频率ω计算,由于色散方程需通过迭代方法求解,为加快计算速度,本文采用下列6 位精度拟合多项式求解

式中,y为无因次波浪频率,系数Cn取值见文献[23].

2 数值计算模型

2.1 模型简介

本文采用一体化仿真软件SIMA (simulation workbench for marine application)开展耦合动力分析.在SIMA 中建立台风经过全程,风浪联合作用下数值模型,塔筒、桩基础、叶片均采用欧拉梁单元建模.单桩基础外径9 m,厚度0.11 m,塔筒为多段等截面梁连接而成,每段梁沿长度方向外径与厚度不变,塔筒底部外径8.16 m,厚度0.07 m,塔筒顶部外径5.65 m,厚度0.03 m.考虑到实际塔筒结构中螺栓、焊接、油漆、法兰及电缆等各种设备的影响,将海床上方塔筒及桩基结构钢的密度考虑为8500 kg/m3,略大于实际中钢的密度7500 kg/m3,弹性模量取210 GPa,剪切模量取80.8 GPa.风力机使用由丹麦技术大学提出的DTU-10 MW 风机,该型风机具有较好的代表性,其主要参数见表1.

表1 DTU 10 MW 风力机参数Table 1 Main parameters of DTU 10 MW wind turbine

本文使用等效桩法考虑桩土作用,模型采用OC6 Phase2[36]中的单桩基础.插入海床中的桩基础总长为28.15 m,外径9 m,内径8.78 m.为模拟泥面线处转角与位移,将插入海床下方的桩基分为两部分,分别具有不同的长度与弹性模量,如图2 所示,图中Ll为23.15 m,L2为5 m,E1为821 GPa,E2为110.89 GPa.

图2 桩土模型示意图Fig.2 Illustration of the soil-structure interaction model

时域模拟采用Newmark-beta 方法求解式(27)所示动力方程,γ为1/2,β为1/4,式中Mt为质量矩阵,Kt为刚度矩阵,由结构构型在时刻t计算得出,分别为位移增量、速度增量、加速度增量.结构阻尼Ct采用了瑞利阻尼,对应一阶模态1%的临界阻尼

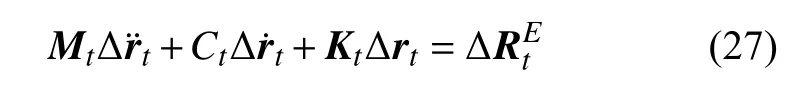
2.2 工况选取

本文重点探究台风经过全程风浪联合作用下大型单桩风机响应,基于文献[8]中实测10 min 平均风速最大值及式(21)～式(23),经浅水修正后计算出台风经过前后眼壁强风区及涡旋前后缘大风区的波浪条件.需要指出,以上公式是基于中国海域大量台风期间海浪实测数据基础上提出的半经验方法,采用国际验证的DTU 10 MW 风机模型,具有一定的局限性.工况如表2 所示.单次模拟时长4000 s,每个工况采用不同种子数后模拟十次,其中,去除400 s 的瞬态反应.坐标系原点位于静水面上塔筒中心处,坐标轴如图3 所示,模拟过程中风浪同向,均沿x 轴正向,实际海况下受海底地形及涌浪影响,风浪不一定同向.风机叶片在模拟开始后变桨至90°,之后一直处于顺桨状态.叶片位置1 竖直向上,位置2、位置3 依次顺时针旋转120°.

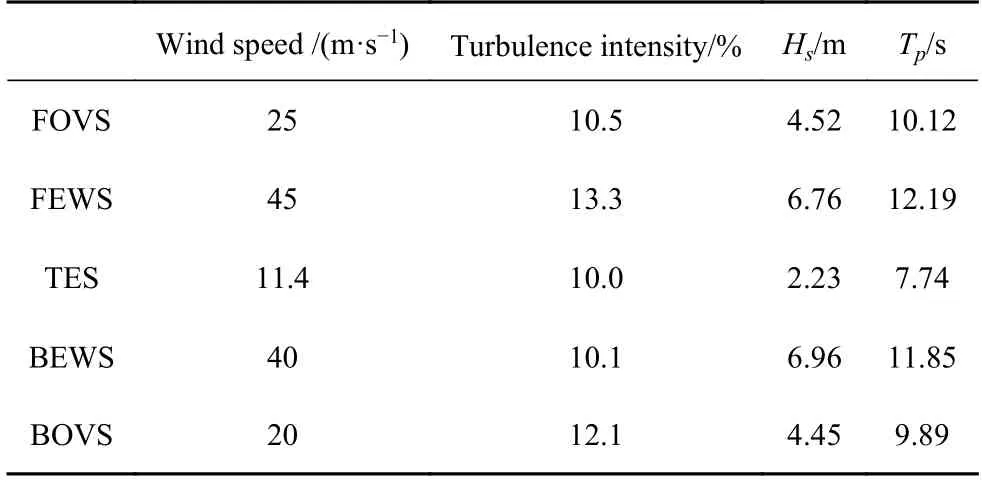
表2 工况定义Table 2 Definition of load cases

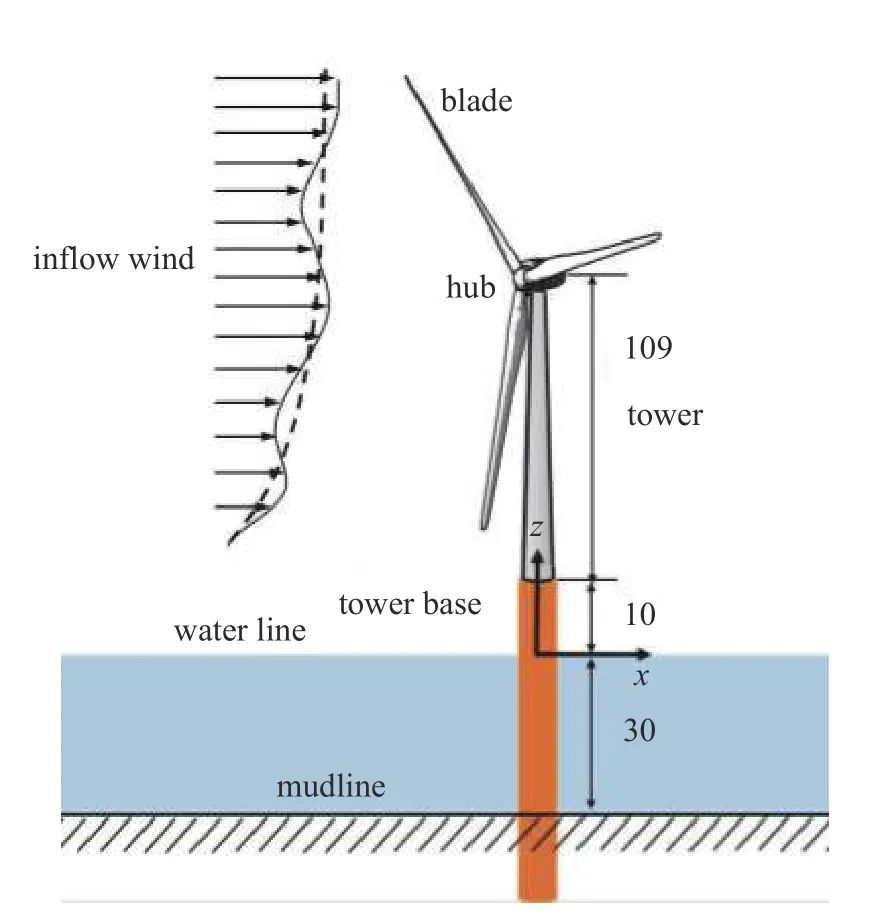
图3 海上风机模型示意图(单位:m)Fig.3 Illustration of the offshore wind turbine model (unit:m)

3 结果与讨论

3.1 台风经过全程运动响应特性分析

对于单桩式海上风力发电机,塔顶、塔基及泥面线运动较能体现出安全性能,因此,本文对以上结果进行对比分析,鉴于篇幅有限,仅给出塔顶运动全过程时程曲线.

图4(a)～图4(c)所示为台风过境全过程塔顶在前后向(FA)运动的时程曲线,图5(a)为塔顶运动的功率谱密度(PSD)图.从时程图可知五阶段塔顶运动具有相似的波动特性,响应谱图显示五阶段运动频率均存在两个峰值,控制频率约为1.7 rad/s,接近塔筒FA 向固有频率,另一峰值较小,接近各阶段波浪频率.同时在风速较高的FEWS 阶段及BEWS 阶段,塔顶运动在低频区域分布有能量.表3 为塔顶运动统计值,表中可见塔顶FA 向运动均值随平均风速增加而增大,且表现出非线性性质:BOVS 阶段至FOVS 阶段、BEWS 阶段至FEWS 阶段平均风速均增加5 m/s,但塔顶运动均值分别增加了0.028 m 与0.06 m,增加了约2 倍,PSD 图也体现出这一点,FEWS 阶段PSD 约为BEWS 阶段两倍.这对设计载荷的准确性提出了较高的要求,高风速下较小的风速差值可能导致较大的响应差别.

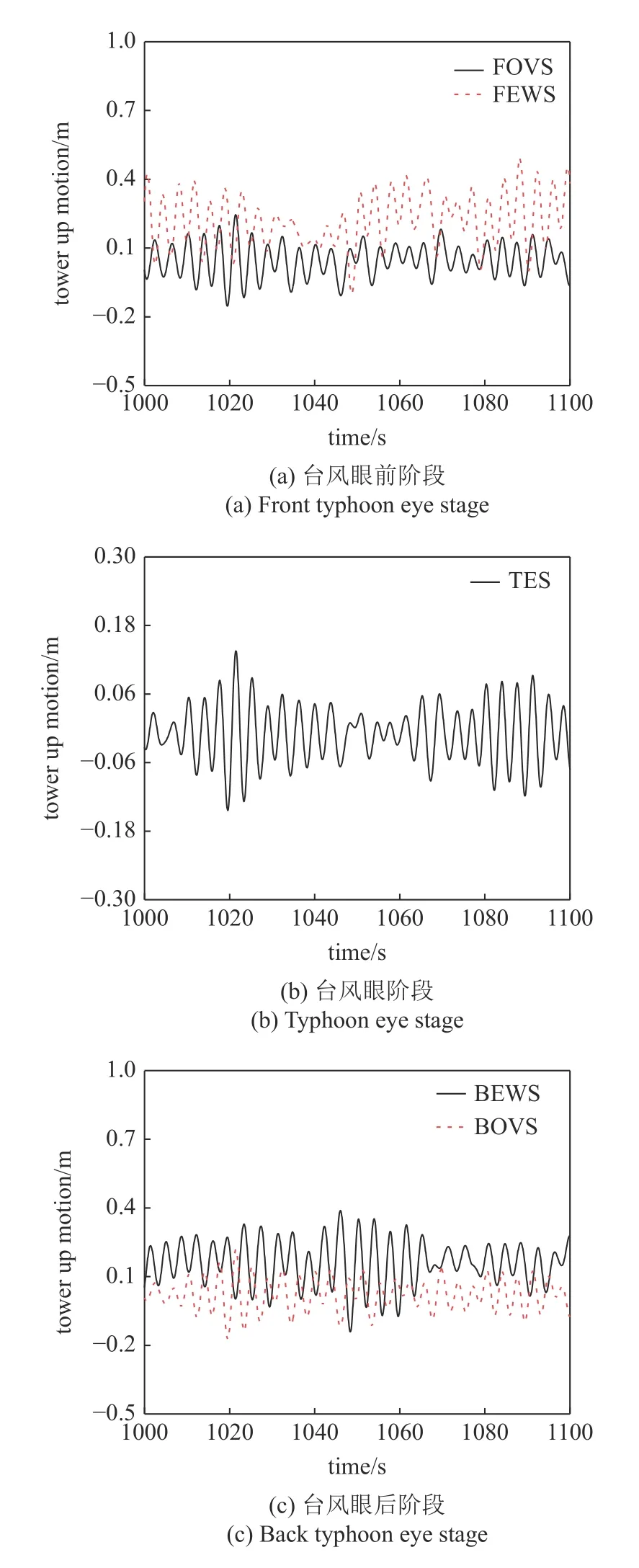
图4 台风经过全过程塔顶FA 向运动响应Fig.4 Tower top-aft (FA) motion during typhoon event

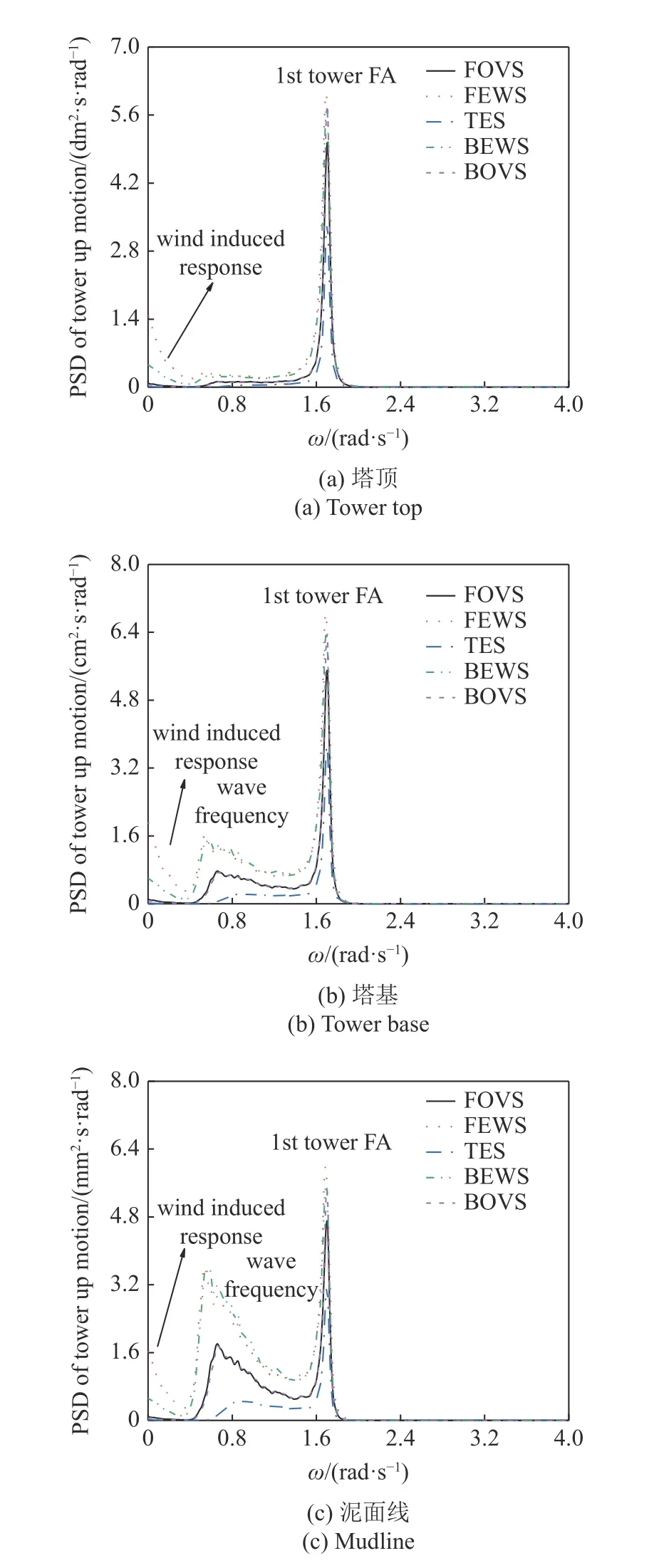
图5 运动响应功率谱密度Fig.5 PSD of motion response

表3 塔顶运动时程统计Table 3 Statistics of tower-top motion

图5(b)和图5(c)分别为塔基、泥面线FA 向运动响应谱,图5(b)中可见台风经过各阶段塔基处运动频率表现出相似特性:各阶段控制频率均为塔筒一阶频率,同时受到波浪频率影响.值得注意的是尽管BEWS 阶段风速及波高均大于BOVS 阶段,一阶频率处BOVS 阶段塔基及泥面线PSD 均大于BEWS 阶段,这可能是由于BEWS 阶段结构的气动阻尼较大.有义波高较低时,波浪激发了塔筒一阶频率,随着有义波高增加,响应谱能量向波频转移.在台风眼区域外,桩基础泥面线处FA 向运动在一阶频率的功率谱密度随风速增高略有增加,但相差不大.

3.2 台风经过全程载荷特性分析

本节将重点分析塔顶、塔基、泥面线处FA 向弯矩与剪力响应,限于篇幅,仅给出FEWS 阶段塔顶动力响应时域曲线.

图6 为台风全过程塔顶剪力时程曲线,图7 为台风经过全过程塔顶、塔基、泥面线处FA 向弯矩及剪力的时程统计图,规定使塔筒向x正向弯曲的弯矩为正,图8 为三个位置处的弯矩及剪力响应谱.

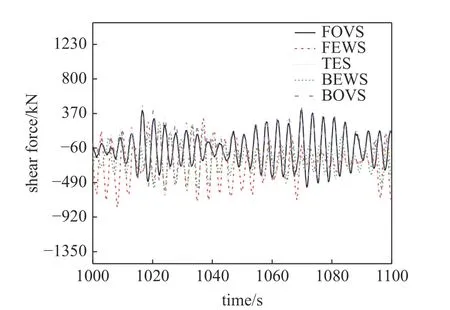
图6 塔顶剪力Fig.6 Tower top shear force

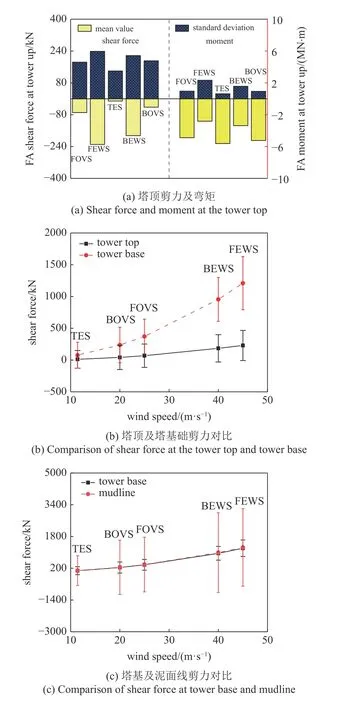
图7 载荷响应统计图Fig.7 Statistics of load response

图6 所示时程曲线在模拟时使用了相同的随机波浪种子及不同的随机风速种子,结果显示在风速较低的TES,FOVS,BOVS 区域塔顶剪力的相位保持一致,而FEWS 阶段及BEWS 阶段则不一致.结合图5(a)可知塔顶剪力波动主要受波浪激发的塔筒运动所引起的惯性力影响.风速较低时,塔筒顶部运动受一阶频率控制,且响应谱较窄,因此同一种子数下塔顶剪力相位一致.风速较高时,塔筒顶部运动PSD 在一阶频率处较宽且在低频及波频处分布有较多能量,因此相位出现离散.从图7(a) 中可见TES 阶段塔顶弯矩均值约-5600 kN·m,FEWS 阶段塔顶弯矩均值约-2800 kN·m,可见风速的增加有助于抵消风力机重力造成的弯矩,但风速增大极大地增加了弯矩的标准差,FEWS 阶段达到了3600 kN·m.塔顶剪力均值反应了上部风机叶片所受风力,图7(b)为塔顶及塔基处剪力均值随风速的变化,由于各风速下剪力均为负值,图中取绝对值.图中可见塔顶剪力均值的最大值出现在FEWS 阶段,约为200 kN,远小于10 MW 风机额定推力1500 kN.可见顺桨有效降低了叶片所受风载荷.且塔顶剪力随风速变化较小,在各阶段变化率接近,而塔基剪力随风速变化较大,高风速下剪力增长率更高.塔基剪力均值来自塔筒及风力机叶片所受风载荷,对比可知变桨停机状态下风力机塔筒所受风载荷远大于叶片.由图7(c)可知泥面线处剪力均值与塔基处接近,但方差远大于泥面线处.

图8 为各截面处剪力和弯矩的PSD 图.由图可知,塔基剪力控制频率为FA 向一阶频率,同时在低频处有风频反应.而泥面线处剪力控制频率则为波浪频率,波浪载荷极大地增加了泥面线处剪力的方差.塔基FA 向弯矩PSD 在各阶段均只存在一个峰值,控制频率为一阶自振频率.泥面线处弯矩PSD 存在两个峰值,各阶段控制频率均为一阶自振频率.

图8 载荷响应功率谱密度Fig.8 PSD of load response

图9 为叶根FA 向弯矩及剪力时程统计图,三个叶片的载荷响应差异明显:图9(a)为叶根弯矩响应统计图,从图中可见各阶段叶片处于位置1 时叶根弯矩均值基本相同,而方差异明显,FEWS 阶段方差接近1500 kN·m.三个位置处叶根弯矩响应方差最大值均出现在FEWS 阶段.图9(b)为叶根剪力统计图,图中可见叶片处于位置2 时叶根剪力均值在三个叶片中最大,且其对风速变化不敏感.综合可知,叶片位于位置2 时处于较危险位置.

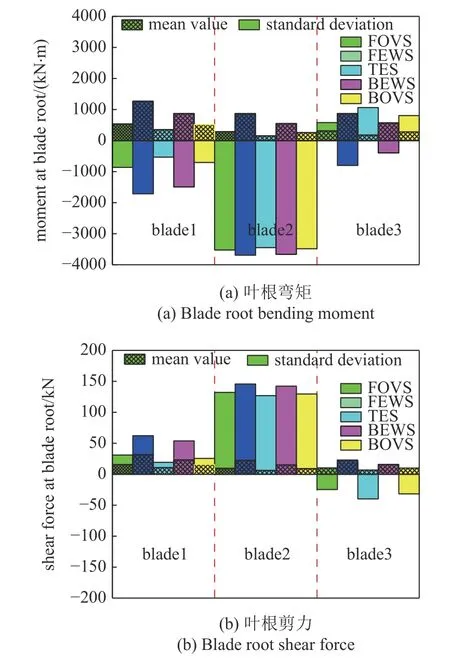
图9 叶片载荷响应统计图Fig.9 Statistics of blade load

4 结论

本文基于DTU 10 MW 风机,应用谐波叠加法模拟台风风场,开展了台风经过全过程风浪联合作用下大型单桩海上风机的耦合动力特性分析,可得出如下结论.

(1) 台风经过全程中,FEWS 阶段风机处于最危险位置,此时塔基及泥面线弯矩均值及标准差最大.

(2) 在风速45 m/s 下时,塔筒运动波动主要受波浪激发一阶频率控制,此时塔基上方各截面处结构动力载荷主要为惯性载荷,同样也受一阶频率控制.而塔基下方泥面线处剪力及弯矩则表现出不同特性:剪力受波浪频率控制,弯矩则受一阶频率控制.同时可看到一方面波高增加时引起的结构固有频率处的响应能量增长有限,响应能量向波频转移.另一方面BEWS 阶段及FEWS 阶段风速相差不大,而塔基及泥面线处低频响应差异较大.因此风速继续增大,波高增加时响应特性可能出现较大变化.

(3)风力机叶片变桨有效降低了叶片所受风载荷,台风经过各阶段中,塔筒所受风力远大于风力机叶片.三个叶片中,叶片处于位置2 时较危险,在台风过后可对处于位置2 的叶片进行针对性检修[37],减少维护成本,同时可开发针对波浪载荷的减振装置,减小台风过境下大型风力机的振动响应.

本文的研究工作仅考虑了单次台风这一特例,由实测台风数据推测海浪要素,重点关注台风过境时风力机响应特性.下一步将基于实测的台风和海浪数据,对风机的长期影响和安全评估进行深入研究.