基于能量传递规律的海洋立管涡激振动抑制研究1)

马烨璇 宋志友 徐万海

(天津大学水利工程仿真与安全国家重点实验室,天津 300072)

引言

海洋立管是深海矿产资源和油气资源开发中的关键设备,亦是薄弱易损构件.海流作用下,立管后缘产生交替泄放的漩涡,诱发立管振动,即“涡激振动(vortex-induced vibration,VIV)”.当漩涡脱落频率接近结构固有频率时,将“锁定”在固有频率附近,致使立管的振动幅值急剧增大,造成严重疲劳损伤,威胁结构安全.因此,立管的涡激振动及抑制一直是学术界和工程界广泛关注的热点和难点问题,已取得了大量代表性的研究成果[1-6].

根据是否有外界能量输入,涡激振动抑制方法可分为两大类:主动抑制和被动抑制.主动抑制通过实时监测结构的振动响应及流场,采用声波、击振等主动方式干扰结构的振动或影响流场.从结构层面考虑,Baz 和Ro[7]设计了适用于柔性圆柱结构多模态涡激振动抑制的独立模态控制器,抑制效率可达40%,但易出现控制溢出现象.Do 和Pan[8]将边界控制技术应用于海洋立管系统,实现了立管在横向、侧向和轴向的稳定性控制.Nguyen等[9]根据Lyapunov 直接法设计了端部控制器,通过控制立管顶端的位移和速度来抑制振动.赵志甲等[10]考虑内流影响,设计了用于立管振动抑制的边界控制装置和干扰观测器.Song等[11]设计了线性二次型最优控制器,有效抑制了立管的多模态振动,抑制效率可达71%～ 89%.赵瑞等[12]提出了通过端部激励对立管进行振动抑制的主动控制技术,分析了端部激励参数对立管振动特性的影响规律.

从干扰流场方面考虑,Cheng等[13]数值模拟了抽吸流体对涡激振动流体力的影响,抽吸速度达到特定范围后,升力幅值显著降低.刘雨[14]实验观测了喷水和喷气两种方式对涡激振动的影响,喷水型装置的间距对抑制效果影响显著,喷气型装置能形成上升气幕,隔断立管尾流,显著降低结构振幅.Zhu等[15]研究了旋转控制杆对涡激振动的抑制效果,旋转控制杆通过向边界层注入动量而推迟边界层分离.柏伟峰[16]提出了抑制涡激振动的行波壁法,将结构后缘改造为行波壁的形式可抑制流动分离,减小平均阻力,通过控制行波壁的波速和波幅能够改进抑制效果.上述主动抑制方法能根据实际环境调整控制参数和控制策略,适应性较强,但技术复杂、工程应用实现难度较大.

相比于主动抑制方法,被动抑制方法较为简单、成本较低,在工程中具有更广阔的应用前景.被动抑制方法主要通过改变结构表面形状或安装附属装置扰乱流场,从而实现抑制振动.基于不同的抑制机理,被动抑制装置分为3 类:表面凸起型,如螺旋列板、表面凸起等;裹覆型,如控制杆和轴向板条等;尾流稳定器型,如整流罩、分离板等[17].分离板能分隔尾流区,是较早被发明的抑制装置,其长度是影响抑制效果的主要参数[18-19].分离板的形式不断被改进,旋转分离板能显著改善稳定性[20],柔性分离板显著提升了振动抑制效果[21].整流罩既能分隔尾流,又能改变边界层分离点的位置,抑制效果优于分离板.整流罩尾端夹角在30°～ 45°之间时,升力系数和平均阻力系数显著降低[22].整流罩存在不稳定问题,可旋转式整流罩能一定程度上增强系统稳定性[23].将整流罩与分离板结合形成短尾整流罩后,能显著增强涡激振动抑制效果[24].

分离板和整流罩等尾流稳定器型装置仅对单一流向效果显著,表面凸起型装置(如螺旋列板)、裹覆型装置(如控制杆) 具有全向性,适应性更强.Quen等[25]研究了螺旋列板的螺头数对抑制效果的影响,螺头数增大至3 后,继续增大螺头数对抑制效果提升有限,反而会增大平均阻力.Gao等[26]研究发现列板高度增大,控制频率、最大位移降低,螺距增大使锁频区的出现延迟,但锁频区的范围增大.Xu等[27]进一步发现圆形截面螺旋列板对涡激振动响应频率和顺流向位移的抑制效果略优于方形截面列板.Ma等[28]实验研究了时变轴向力作用下螺旋列板对立管涡激振动的抑制效果,时变轴向力激励使螺旋列板的抑制效率降低.Xu等[29]研究了攻角来流作用下螺旋列板的抑制效果,随着来流攻角增大,螺旋列板的抑制效率显著降低.立管周围通常存在附属小管缆,合理布置后,能干扰边界层的发展,起到控制杆的效果.Wu等[30]关注了控制杆覆盖率和间距比对抑制效果的影响,覆盖率达到80%、间距比为0.187～ 0.562 时,抑制效果较好.Lu等[31]研究了控制杆个数和安装角度对抑制效果的影响,4 根控制杆的安装角度为45°时,抑制效率可达90%.Xu等[32]实验观测了攻角来流作用下控制杆抑制效果,控制杆对涡激振动的抑制效率受来流攻角影响较小.

目前,立管涡激振动的被动抑制方法主要通过干扰流场的方式,需要额外安装附属装置.在复杂环境条件下,常见抑制装置对流场的干扰作用减弱,抑制效果下降[28-29].因此,从结构自身层面考虑,抑制立管的涡激振动十分必要.刘文博[33]采用弹簧振子减振器抑制刚性圆柱结构涡激振动,探究了减振器质量比、阻尼比和刚度比对振动位移、响应频率、锁频区域的影响.Dai等[34]基于尾流振子模型研究了非线性减振器对圆柱结构涡激振动的抑制效果.减振器的质量和阻尼参数对减振器的吸能效果影响显著,改变减振器的参数能使结构发生周期振动、准周期振动及非周期振动.

从结构角度抑制涡激振动的研究中关注对象多为刚性圆柱结构,针对立管这类柔性圆柱结构振动抑制的研究仍十分有限.本文基于能量传递的思想,通过增大能量耗散区阻尼实现立管振动抑制,采用理论模型对抑制效果进行分析,以期为工程中海洋立管的涡激振动抑制提供参考和借鉴.

1 基于能量传递的振动抑制理论

涡激振动是典型的流固耦合问题.立管发生涡激振动时,沿结构轴向可划分出如图1 所示两类区域,能量输入区和能量耗散区.流固耦合过程中,在能量输入区,流体能量转移至结构,激发结构振动,在能量耗散区,振动能量被消耗.Vandiver等[35]阐述了立管涡激振动过程中,行波能量沿轴向的传递过程.

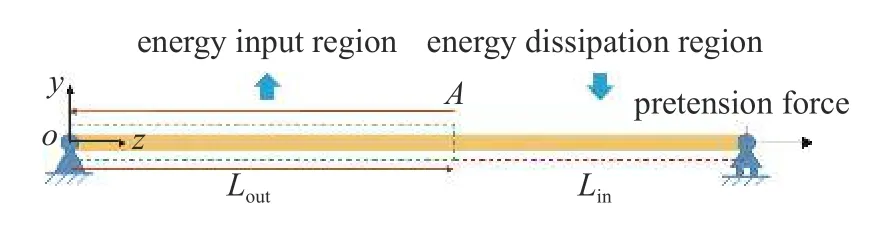
图1 立管涡激振动过程中的能量传递示意图Fig.1 Schematic diagram of energy conduction during the vortexinduced vibration

立管振动过程中,振动能量由能量输入区传递至能量耗散区.在能量耗散区,结构振动表现为行波特征,能量沿立管轴向传递,行波行进过程中产生能量消耗.行波携带的能量传递至立管端部后产生反射,再次穿过能量耗散区后,重新进入能量输入区.能量输入区和能量耗散区边界点A处,行波的能量可表示为

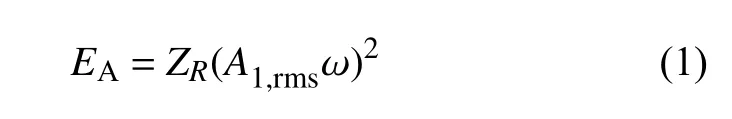
式中,ZR为阻抗的实部,A1,rms表示能量输入区和能量耗散区边界处的振动位移均方根,ω为振动圆频率.假设能量输入区内立管振动近似简谐形式,则(A1,rmsω)2可表示能量输入区和能量耗散区边界处振动速度均方根的平方.

基于波传播的理论,立管的振动响应可以采用行波和表面波叠加的方式表示

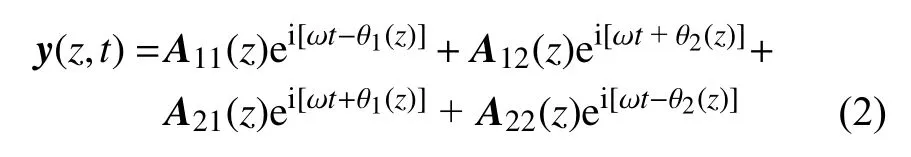
式中,A11(z)和A21(z)分别表示向正负两个方向传播的行波幅值,A12(z)和A22(z)分别表示向正负两个方向传播的表面波幅值.θ1(z)和θ2(z)的表达式为

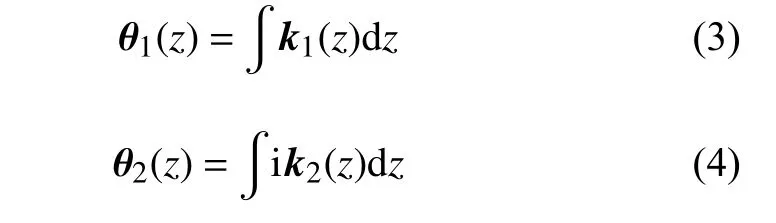
式中,k1(z)为行波波数,ik2(z)为表面波波数.假定行波沿立管轴向只沿正向传播,式(2)中立管振动响应表达式可简化为

k1(z)和k2(z)满足如下的色散关系

式中,T(z)为轴向力,m(z)为单位长度的质量,c(z)为阻尼,EI(z)为弯曲刚度.立管的载荷与速度的关系如下

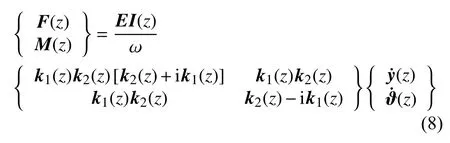
式中,F(z)为立管横向受力,M(z)为立管的弯矩载荷,分别表示振动速度和转动速度.由于表面波仅影响结构在激励源处的响应,结构远离激励源的振动响应可表示为

通过立管某一截面处的能量可用载荷与速度表示为

式中,*表示复共轭.将式(8)和式(9)代入式(10),可得到ZR(z)的计算公式

在A点设立局部坐标系,A点为零点.振动能量由A点经过能量耗散区传递至端点过程中的能量衰减比为

式中Lout为能量耗散区长度,c(s)为单位长度阻尼.

行波能量在立管中的传递主要受立管质量、阻尼、弯曲刚度、轴向力参数的影响,立管的边界条件对能量沿立管的传递规律影响不大.波传播至立管边界处,会发生反射和透射现象,出现能量损失.实际工程中,深海立管的底部采用挠性接头连接,底部边界条件可视为简支.在理论推导行波传播的能量耗散时可忽略行波传播至立管底边界处的能量损失,认为波在立管底边界完全反射.

因此,行波传递至端点发生反射会再次经过能量耗散区并进入能量输入区.由端点反射后穿过能量耗散区再次到达A点的振动能量也发生耗散,能量衰减比与式(12)中的能量衰减比相同.再次经过A点的振动能量与最初经过A点的振动能量比为

假定能量比不超过1%时,便近似认为由能量输入区传出的能量在耗散区完全被消耗,即

求解式(15)可得βR≥2.3.表明当能量衰减系数βR≥2.3 时,能量输入区传出的能量在能量耗散区完全被耗散,立管的振动将被显著抑制.基于上述理论分析,可以通过增大立管在能量耗散区的阻尼使βR≥2.3,从而抑制立管振动.

2 立管涡激振动理论模型

2.1 理论模型

首先,通过理论模型研究基于能量传递的立管振动抑制方法的可行性.基于尾流振子模型模拟立管与尾流之间的相互作用,立管采用欧拉-伯努利梁模型,横流向的振动控制方程为

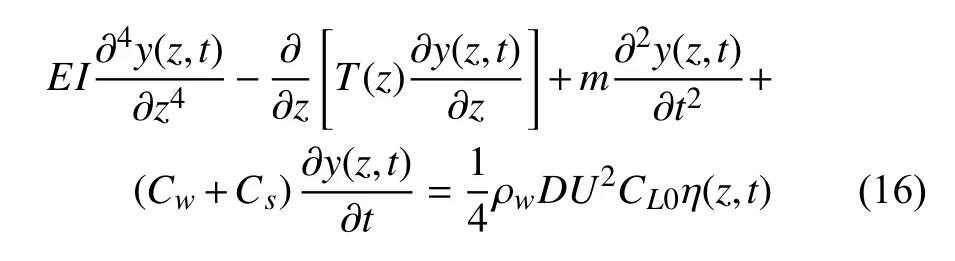
式中,y(z,t)为横流向振动位移,η(z,t)为振子变量,z为轴向坐标,t为时间.E为杨氏模量,I为转动惯量,D为立管外径,Cs为结构阻尼系数.ρw为外流密度,U为外流速度.CL0为固定圆柱的升力系数,取为0.3.m为单位长度的质量,包括结构质量ms和附加质量ma=0.25πρD2.T(z)为轴向力,表达式如下

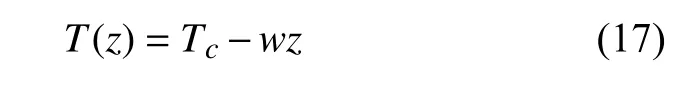
式中,Tc为初始轴向力,w为立管单位长度的湿重.Cw为水动力阻尼,如下式

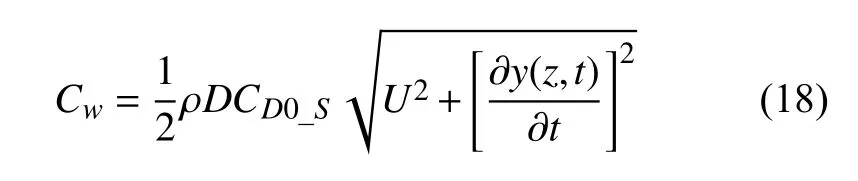
式中,CD0_S为固定圆柱的平均阻力系数,可取为1.2.采用尾流振子模型模拟尾涡与立管之间的相互作用

其中St为斯托罗哈数.A和ε为经验参数,取A=12,ε=0.3.联立式(16)和式(19),采用有限差分法将立管模型沿轴向进行空间离散.有限差分格式如下

式中,N为单元个数,h=L/N为单元长度.立管两端的边界条件为简支,边界处的差分格式为

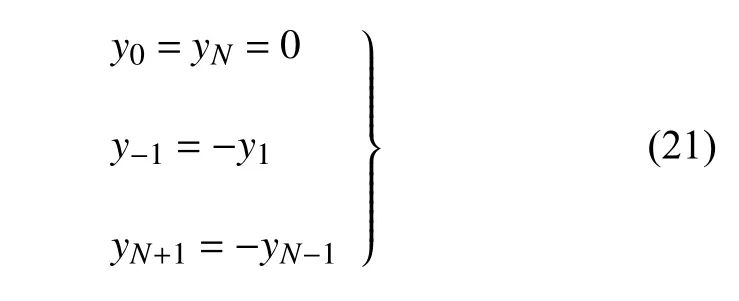
通过有限差分法将式(15)和式(18)联立得到的偏微分方程转化为常微分方程组,采用Runge-Kutta 法进行迭代求解.

2.2 模型验证

基于海洋立管涡激振动模型实验结果对涡激振动理论模型进行验证.分别选取了Ma等[36]和Franzini等[37]开展的均匀来流作用下模型实验参数,计算了立管涡激振动响应.Ma等[36]开展的模型实验中立管模型水平浸没在水中,可不考虑立管自重的影响.Franzini等[37]开展的模型实验中,立管垂直水池底面浸没在水中,需考虑自重的影响.相关的实验参数如表1 所示.Ma等[36]开展的模型实验和Franzini等[37]开展的模型实验中,立管两端的边界条件均可视为简支.

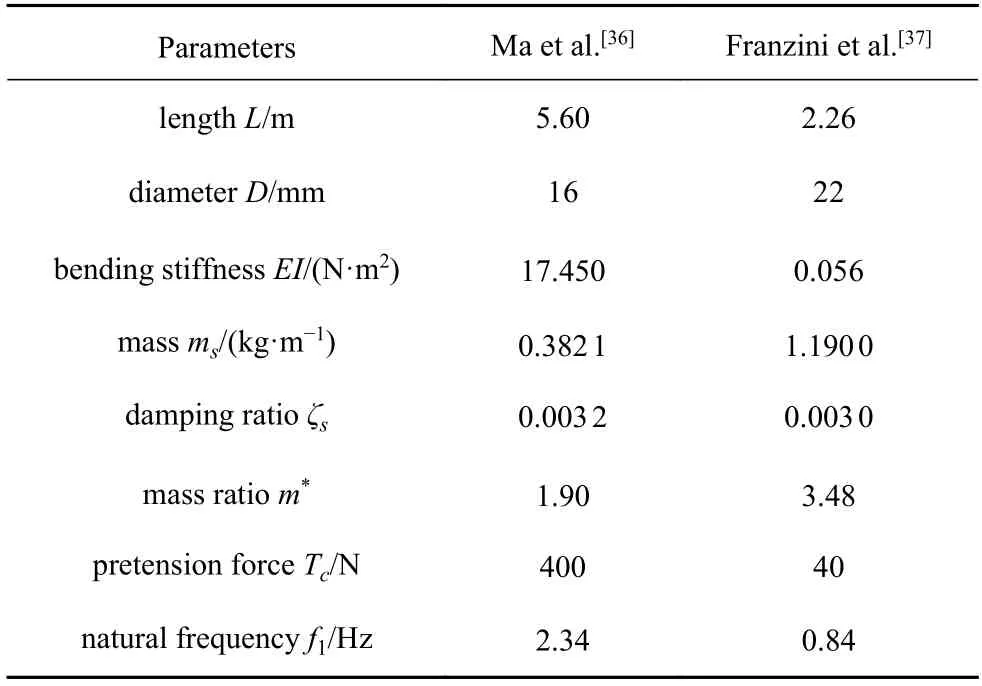
表1 立管模型实验中的主要参数Table 1 Major parameters in riser model tests

Ma等[36]开展的模型实验中,约化速度为24.0 时,立管模型激发3 阶振动模态.采用理论模型计算了约化速度24.0,对应来流速度0.90 m/s 工况下的立管振动响应,无量纲位移均方根的轴向分布结果如图2 所示.理论模型计算得到的位移均方根分布也表现为3 阶模态振型,结果略高于实验结果,但整体吻合较好.

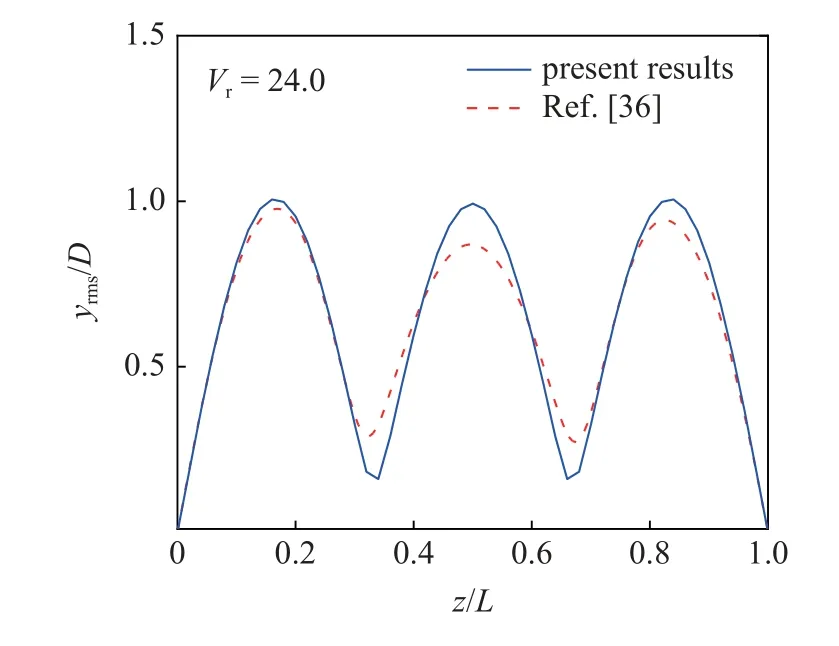
图2 理论模型结果与文献[36]的实验结果对比Fig.2 Comparison between the present results and the results in Ref.[36]

Franzini等[37]开展的实验中,立管模型主要激发一阶模态.采用理论模型计算了约化速度5.6,对应来流速度0.10 m/s 工况下的立管振动响应,无量纲的位移轴向分布结果如图3 所示.Franzini等[37]的实验中给出了立管模型前10%最大无量纲位移的均值.因此,选取横流向振动的前10%最大无量纲位移的均值结果进行对比.理论模型计算得到的最大位移为0.64D,实验观测的最大位移为0.66D.理论模型结果与实验结果整体吻合较好,验证了立管涡激振动理论模型的准确性.

图3 理论模型结果与文献[37]的实验结果对比Fig.3 Comparison between the present results and the results in Ref.[37]

理论模型结果仍与实验结果存在一定的差异,产生差异的主要原因有两方面.一是基于尾流振子模型计算立管涡激振动响应时仅关注了横流向振动,并未考虑顺流向振动的影响.实验中,立管模型在横流向和顺流向两个方向同时振动,顺流向振动会对横流向振动响应产生一定影响.二是在理论模型中并未考虑附加质量系数和平均阻力系数的变化.立管涡激振动过程中,附加质量系数和平均阻力系数会随响应频率和响应幅值发生变化.而在理论模型中附加质量系数取为1.0,平均阻力系数取为1.2.

3 结果分析

3.1 能量耗散区识别

为了判断立管涡激振动的能量输入区和能量耗散区,需要基于理论公式计算立管涡激振动过程中的能量系数[38],公式为

式中,CE(z)为能量系数,表示流体输入结构的能量.根据能量系数的大小可判定能量输入区和能量耗散区.Ts为振动时长,y˙(z,t) 为振动速度,U(z)为外流速度.fy(z,t)为流体力,即

以工程中的立管为例,分析基于能量传递的涡激振动抑制方法的效果.基于能量传递的振动抑制理论,局部增大能量耗散区的阻尼,使βR≥2.3 后便能抑制立管振动.因此,需要对能量耗散区进行识别.分析的立管参数来自英国BP 石油公司的深水Spar平台,主要参数如表2 所示.外流为顶部流速为0.5 m/s的剪切流,如图4 所示.

表2 立管的主要参数Table 2 Major parameters of the riser

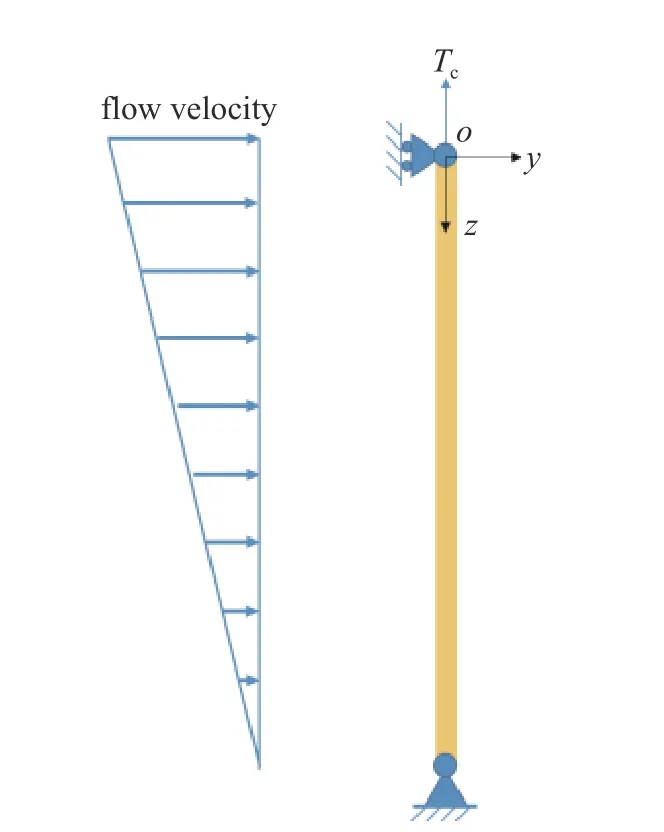
图4 立管示意图Fig.4 Schematic diagram of the riser

采用理论模型计算了立管在顶部流速为0.5 m/s的剪切流作用下的涡激振动响应.位移均方根分布如图5 所示.在选取的来流工况下,立管振动模态为14 阶,第14 阶模态固有频率为0.30 Hz.立管上部振动呈行波特征,最大位移均方根出现在z/L=0.3 附近.立管底部振动呈显著的驻波特征,位移均方根也处于较高的水平.

图5 位移均方根轴向分布Fig.5 Axial distribution of root mean square of displacements

图6 为立管振动位移云图和位移频谱图.从位移云图中可明显观察到立管上部振动的行波特征,行波传播方向为z/L=0至z/L=1.0.立管底部,即z/L=1.0 附近,振动呈显著的驻波特征.主要是行波传递至立管底端,在底边界反射后,反射波与入射波叠加导致的.从频谱图中观察到,立管振动存在若干个窄频成分,控制频率成分接近第14 阶模态的固有频率.其他谐波成分较为接近控制频率,表明了立管涡激振动的多模态特征,主控模态的相邻模态对振动仍具有显著贡献.立管振动的频谱特性不沿轴向发生显著变化.

图6 位移云图和频谱图Fig.6 Displacement contour and frequency spectrum

图7 为立管涡激振动的能量系数沿轴向的分布情况.由图中可以发现立管上半部分的能量系数较高,而下半部分的能量系数较低.能量系数的分布情况表明立管上半部分为能量输入区,能量耗散区大致位于z/L=0.6～ 1.0 段.

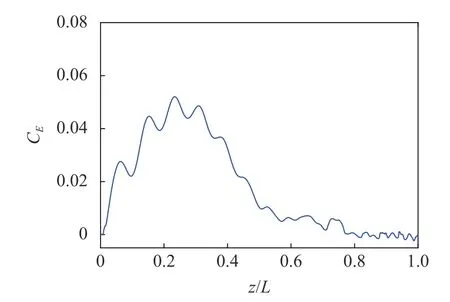
图7 能量系数的轴向分布Fig.7 Axial distribution of the energy coefficient

3.2 振动抑制效果

通过局部增大能量耗散区阻尼的方式来增大βR,使其超过2.3,以实现对振动的抑制.式(13)中的阻尼项c(s)既包括结构阻尼Cs又包括水动力阻尼Cw.结构阻尼通过阻尼比的方式计算,水动力阻尼根据式(18)计算.通过增大结构阻尼和水动力阻尼的方式均能增大能量衰减系数.为了简便,在分析振动抑制效果时采用了增大结构阻尼的方式来增大能量衰减系数.

在所选取的外流工况下,通过能量系数的结果得到的能量耗散区为z/L=0.6～ 1.0 段.将能量耗散区分为两段,分别在z/L=0.6～ 0.8和z/L=0.8～1.0 局部增大阻尼来检验振动抑制效果.同时为了进一步验证行波传播能量主要在能量耗散区发生损耗,额外设置了3 种局部阻尼增大区域,即z/L=0～0.2,z/L=0.2～ 0.4和z/L=0.4～ 0.6 段(如图8 所示).

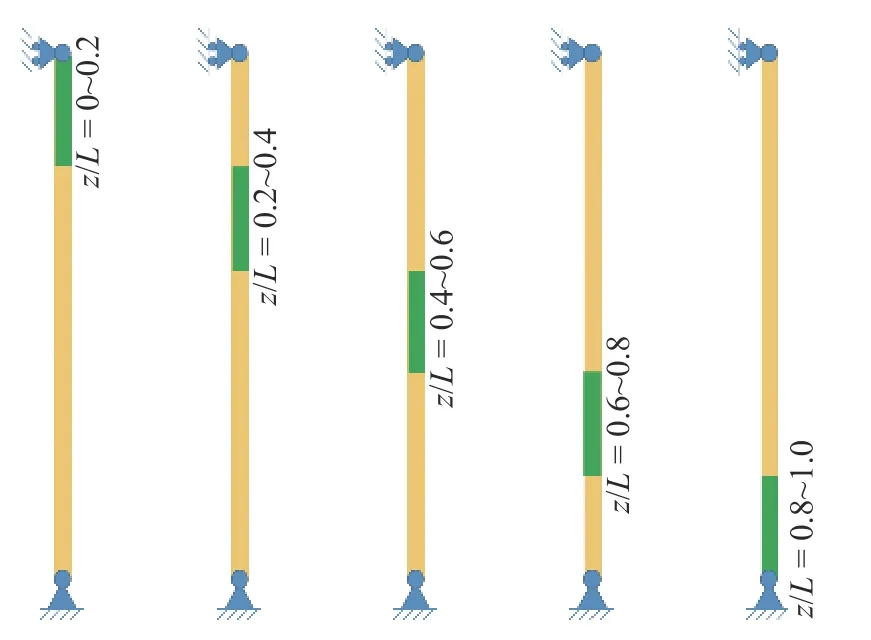
图8 立管局部阻尼增大区域示意图Fig.8 Schematic diagram of the local damping increase region

采用增大结构阻尼比的方式增大立管局部阻尼.图9 给出了立管z/L=0.8～ 1.0 段不同阻尼比对应的βR值.结构的初始阻尼比为0.003,分别将结构阻尼比增大0.05,0.08,0.10,0.15,阻尼比增大后的值分别为0.053,0.083,0.103,0.153.立管z/L=0.8～1.0 段阻尼比为上述值时,对应的βR分别为1.3,2.0,2.5 和3.6.阻尼比为0.053 时,βR远小于2.3;阻尼比为0.083 时,βR略小于2.3;阻尼比为0.103 时,βR略高于2.3;阻尼比为0.153 时,βR远高于2.3.

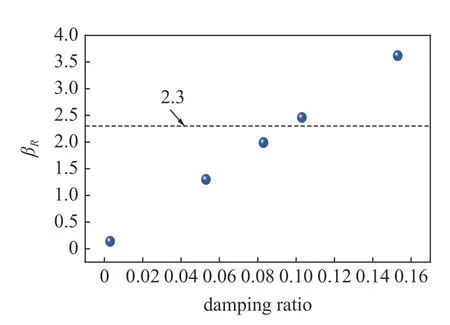
图9 z/L=0.8～ 1.0 段不同阻尼比对应的βR值Fig.9 Values of βR corresponding to different damping ratios at z/L=0.8～ 1.0

图10 为立管z/L=0～ 0.2 段阻尼增大后的位移均方根轴向分布.z/L=0～ 0.2 段阻尼增大后,立管位移均方根整体呈降低趋势.但增大阻尼后位移均方根的轴向分布趋势未发现显著变化,立管上部接近z/L=0.3 处和立管底部的振动位移较高.阻尼比为0.053,0.083,0.103 和0.153 时,位移均方根的平均降低幅度分别为19.3%,28.8%,28.7%和28.0%.当阻尼比增大至0.083 后,继续增大阻尼比,位移均方根平均降幅基本保持不变.

图10 z/L=0～ 0.2 段阻尼增大后的位移均方根Fig.10 Root mean square of displacements after increasing damping ratio at z/L=0～ 0.2

图11 为立管z/L=0.2～ 0.4 段阻尼增大后的位移均方根轴向分布.z/L=0.2～ 0.4 段阻尼增大后,立管位移均方根略有降低.立管上部和底部的位移仍然较高,阻尼比对位移均方根的影响规律并不明显.阻尼比为0.053,0.083,0.103 和0.153 时,位移均方根的平均降低幅度分别为17.1%,26.4%,26.5%和21.7%,表明在能量输入区增大阻尼对振动幅值的抑制效果并不显著.

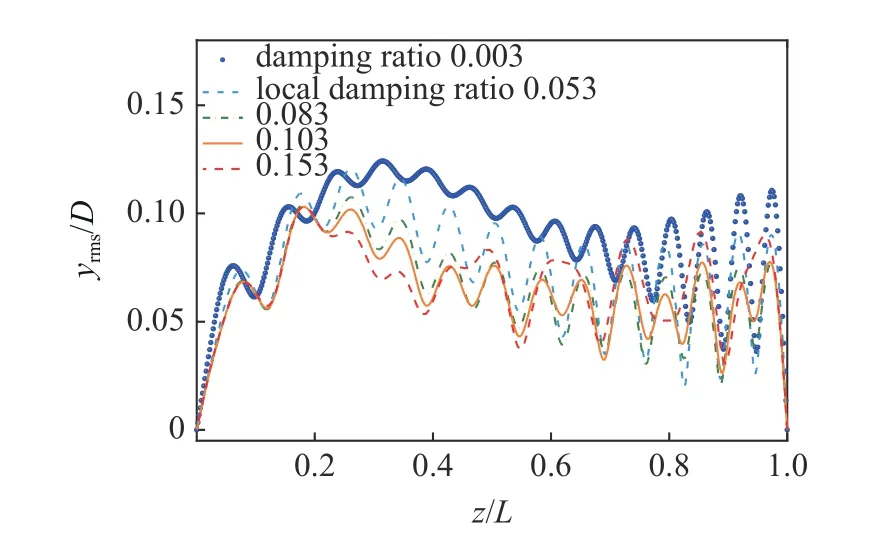
图11 z/L=0.2～ 0.4 段阻尼增大后的位移均方根Fig.11 Root mean square of displacements after increasing damping ratio at z/L=0.2～ 0.4

图12 为立管z/L=0.4～ 0.6 段阻尼增大后的位移均方根轴向分布.z/L=0.4～ 0.6 段阻尼增大后,立管上部的位移均方根仍然较高,底部的位移均方根低于上部但整体水平仍然较高.阻尼比为0.053,0.083,0.103 和0.153 时,位移均方根的平均降低幅度分别为18.3%,28.5%,31.5%和34.7%.

图12 z/L=0.4～ 0.6 段阻尼增大后的位移均方根Fig.12 Root mean square of displacements after increasing damping ratio at z/L=0.4～ 0.6

图13 为立管z/L=0.6～ 0.8 段阻尼增大后的位移均方根轴向分布.z/L=0.6～ 0.8 段位于能量耗散区,阻尼增大后,对振动的抑制效果较为显著.阻尼比为0.053,0.083,0.103 和0.153 时,位移均方根的平均降低幅度分别为29.4%,48.0%,51.6%和55.1%.阻尼比为0.053 时,立管上部的位移略有降低,底部位移的下降幅度相对较高,表明在能量耗散区增大阻尼后,行波传递过程中,能量产生损耗.但由于阻尼增大有限,βR远小于2.3,行波能量并未完全损耗,行波在底边界反射后仍与入射波叠加形成了较为明显的驻波振动,仍有较高能量返回至能输入区,使立管的上部振动位移较高.当阻尼比增大至0.083 时,βR略小于2.3.行波能量在能量耗散区被大量耗散,立管底部的振动位移显著降低.较少的能量返回至能量输入区,使立管上部的振动位移也显著降低.当阻尼比增大至0.103 时,βR略大于2.3.近似可认为行波能量在能量耗散区完全耗散,立管上部位移和底部位移略低于阻尼比为0.083 时的结果.当阻尼比增大至0.153 时,βR远大于2.3.立管上部的振动位移与阻尼比为0.103 时的结果基本一致,表明βR超过临界值后,行波能量在能量耗散区几乎完全耗散,没有能量再返回至能量输入区.立管底部的振动位移略低于阻尼比为0.103 时的结果.上述结果表明当βR超过临界值后,继续增大能量耗散区的阻尼仅能有效降低能量耗散区的振动幅值,对能量输入区的振动位移影响极小.

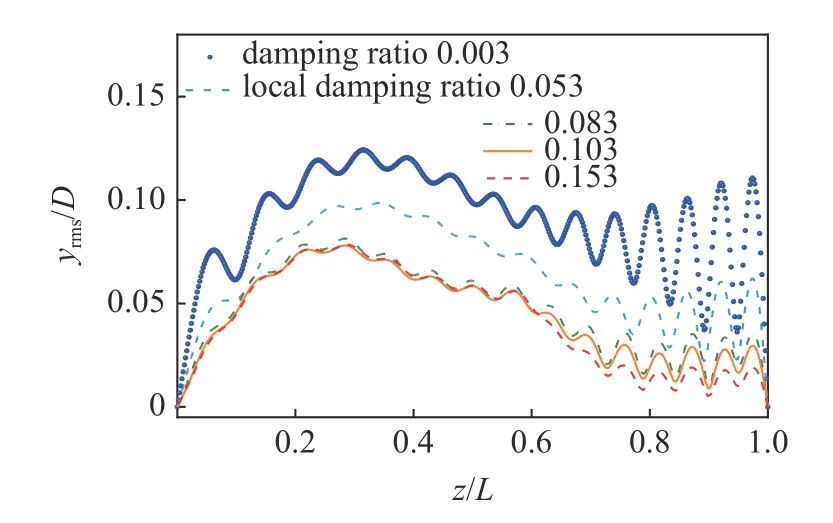
图13 z/L=0.6～ 0.8 段阻尼增大后的位移均方根Fig.13 Root mean square of displacements after increasing damping ratio at z/L=0.6～ 0.8

图14 为立管z/L=0.8～ 1.0 段阻尼增大后的位移均方根轴向分布.z/L=0.8～ 1.0 段位于能量耗散区,阻尼增大后,对振动的抑制效果也较为显著.阻尼比为0.053,0.083,0.103 和0.153 时,位移均方根的平均降低幅度分别为28.3%,44.1%,44.0% 和47.8%.阻尼比为0.053 时,由于阻尼较低,行波传递过程中能量耗散有限,立管上部的位移仍然较高.阻尼比为0.083 和0.103 时,βR接近2.3.行波振动能量在能量耗散区得到充分耗散,立管上部位移和底部位移显著降低.阻尼比为0.153 时,βR超过临界值,继续增大阻尼,振动位移并未显著下降.对比z/L=0.6～ 0.8 段阻尼增大的结果,立管最大位移基本接近.由于z/L=0.6～ 0.8 段阻尼增大时,行波传播至z/L=0.6 时能量开始耗散,而在z/L=0.8～ 1.0 段增大阻尼时,行波传播至z/L=0.8 时能量才开始耗散.z/L=0.8～ 1.0 段增大阻尼时,z/L=0.6～ 0.8 段的振动位移相对更高.

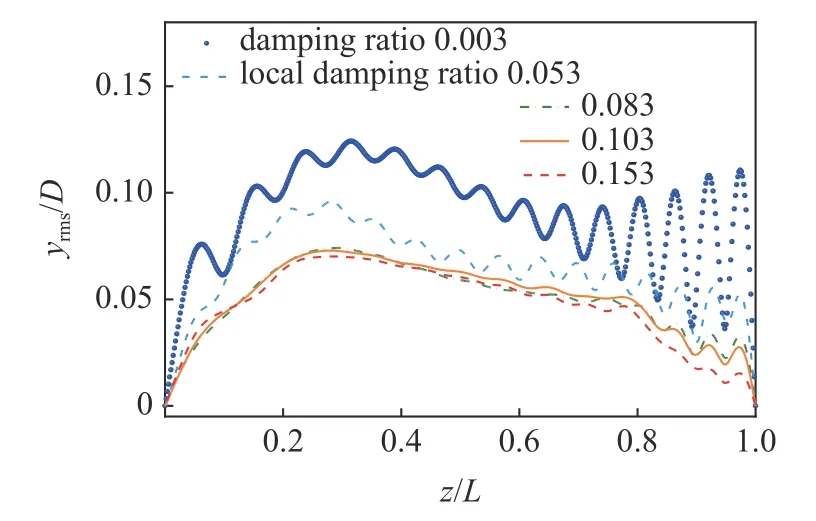
图14 z/L=0.8～ 1.0 段阻尼增大后的位移均方根Fig.14 Root mean square of displacements after increasing damping ratio at z/L=0.8～ 1.0

图15 为立管z/L=0.8～ 1.0 段阻尼比增大至0.103 后的位移云图和位移频谱图.相对于图6 中阻尼未增大的结果,立管的整体振动位移降低.振动表现为显著的行波特征,行波传播方向为由立管上部至立管底部.阻尼增大后,位移云图变化的规律性相比阻尼增大前减弱.位移频谱图中存在多个频率成分,频谱沿轴向发生变化.在z/L=0.2～ 0.5 段,第14 阶模态的固有频率0.3 Hz 附近存在4 个显著频率成分,为主控模态及其相邻模态频率.在z/L=0.5～0.8 段,0.30 Hz 附近的频率成分减弱,同时出现接近0.17 Hz 的低频成分.在z/L=0.8～ 1.0 段,振动位移显著降低,其他区域观测到的频率成分逐渐消失.

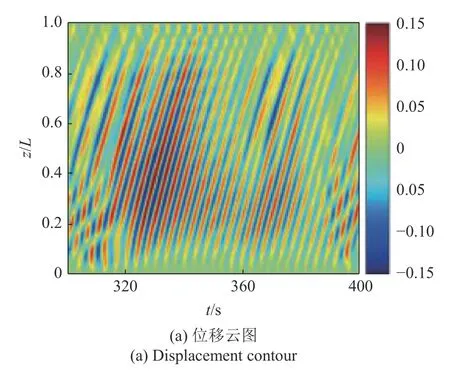
图15 位移云图和频谱图(z/L=0.8～ 1.0 段阻尼比为0.103)Fig.15 Displacement contour and frequency spectrum (damping ratio is 0.103 at z/L=0.8～ 1.0)

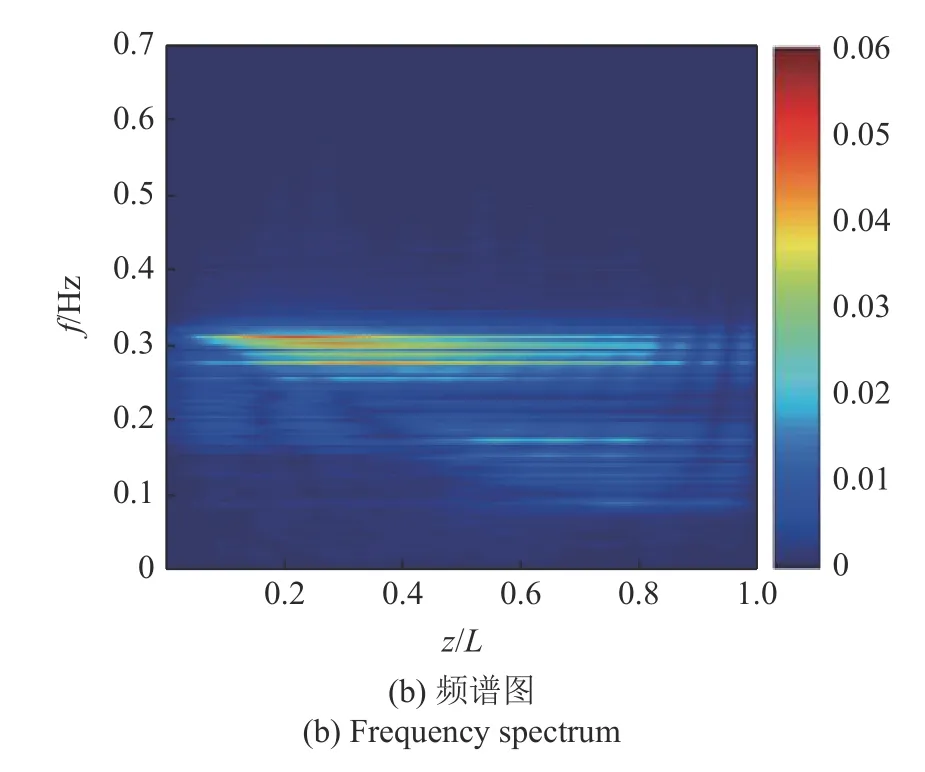
图15 位移云图和频谱图(z/L=0.8～ 1.0 段阻尼比为0.103)(续)Fig.15 Displacement contour and frequency spectrum (damping ratio is 0.103 at z/L=0.8～ 1.0)(continued)

4 结论

本文基于能量传递的理论,通过增大结构阻尼对立管涡激振动进行抑制.根据构建的立管涡激振动理论模型,验证了振动抑制方法的有效性,主要结论如下.

(1)立管发生涡激振动时,沿轴向存在能量输入区和耗散区.通过理论计算的能量系数可判定能量输入区和耗散区的位置.振动能量以行波形式由能量输入区传播至耗散区,主要在耗散区被消耗.

(2)剪切流作用下,立管上部和底部位移较高.增大能量输入区的阻尼后,立管振动位移略有降低,对振动的抑制效果并不显著.

(3)增大能量耗散区的阻尼,使能量衰减系数达到临界值后,由能量输入区传递至耗散区的振动能量被完全耗散,不再返回至能量输入区.立管的底部和上部振动位移均显著下降.但当能量衰减系数达到临界值后,继续增大阻尼,振动位移的降幅不显著.

实际工程中,海洋立管涡激振动的能量输入区多位于中上部,能量耗散区接近立管底部.通过在能量耗散区裹覆阻尼材料,使能量衰减系数接近临界值,确保振动中传递的能量在能量耗散区被尽可能多的耗散.阻尼需要增大的数值可根据能量衰减系数的临界值计算.