基于大数据技术的智能旅游数据间的相关性分析及应用研究

刘 燕

(西安欧亚学院，陕西 西安 710065)

随着互联网及通信技术的不断发展，旅游信息处理和交易的方式已从传统面对面转变成电子方式，因此留下了大量与旅游有关的电子痕迹[1]。这些电子痕迹包括种类繁多、数量庞大的旅游信息，如出行前的规划和信息搜索、预订，和预订、出行后的体验分享与推荐，以及照片上传和其他社交媒体互动活动。这些大型的、非结构化的、复杂的电子痕迹构成旅游大数据，可对其进行整合和分析，以揭示旅游领域中隐藏的模式、相互关系等[2]。

为此，国内外众多学者对旅游大数据进行研究，并取得了丰硕的研究成果。刘逸等[3]利用大数据分析揭示了旅游目的地情感评价模型；张建涛等[4]构建以大数据平台为依托的智慧旅游预测与反馈的服务平台，并提出了实现智慧旅游服务平台的构建模式与路径。大数据分析也被用来预测游客流量。戴文[5]以南京智慧旅游大数据运行监测平台为基础，构建了南京市旅游流量预测模型。Gunter和Onder测试了维也纳旅游目的地管理组织(DMO)谷歌分析公司(Google Analytics)的10个交通指标，通过应用自回归模型(Vector Autoregressive，VAR)建模的大数据收缩方法预测维也纳的游客数量。

上述方法很少有对旅游大数据进行形式化定义，且没有对旅游大数据中涉及要素之间的关系进行探讨。为此，本文首先定义旅游大数据五维范式模型，并对旅游大数据中天气、温度、周末和公共假期与目的地游客到达量和目的地搜索热度的相关性进行研究，利用VAR和Granger因果检验探索目的地实际到达人数与其搜索热度之间的关系。

1 相关知识

1.1 大数据构成

一般情况下，大数据可描述为一个五维范式，即

Bd=[Vnum,Vvar,Vsp,Vper,Vval]

(1)

式中：Vnum描述数据量，代表海量的数据；Vvar描述数据类型，代表来自不同来源、具有异构格式的各种数据；Vsp描述速度，指以采集速度实时或接近实时的数据处理；Vper描述准确性，指数据中存在的不确定性、噪声和异常值；Vval描述价值，反映了统计和分析方法揭示的信息，包括直接价值或隐藏价值。因此，如果只谈论数据量，“大数据”一词的定义仍然不明确。重要的不是大量的数据，而是从中提取隐藏的信息，使之有意义并探索其价值。

图1为本文研究的旅游大数据包含的数据源，具体有票价信息、天气、温度、周末、公共节假日和搜索热度6个部分。随着时间的推移，每天的票价、天气、温度、周末和公共假期的数据量越来越大，同时庞大的搜索热度量由无数的出行信息数据(痕迹)组成，这些构成了旅游大数据的Vnum。旅游大数据的Vvar包括传统的结构化数据、半结构化数据和非结构化数据，其中每日票价是传统数据；天气、温度、日历信息(周末和公共假日)是半结构化数据；基于网络的搜索查询(如文本、图像和视频等)是非结构化数据。速度Vsp和准确性Vper可以通过数据捕获、存储和转换过程来体现，而价值Vval则通过数据分析来揭示隐藏信息。

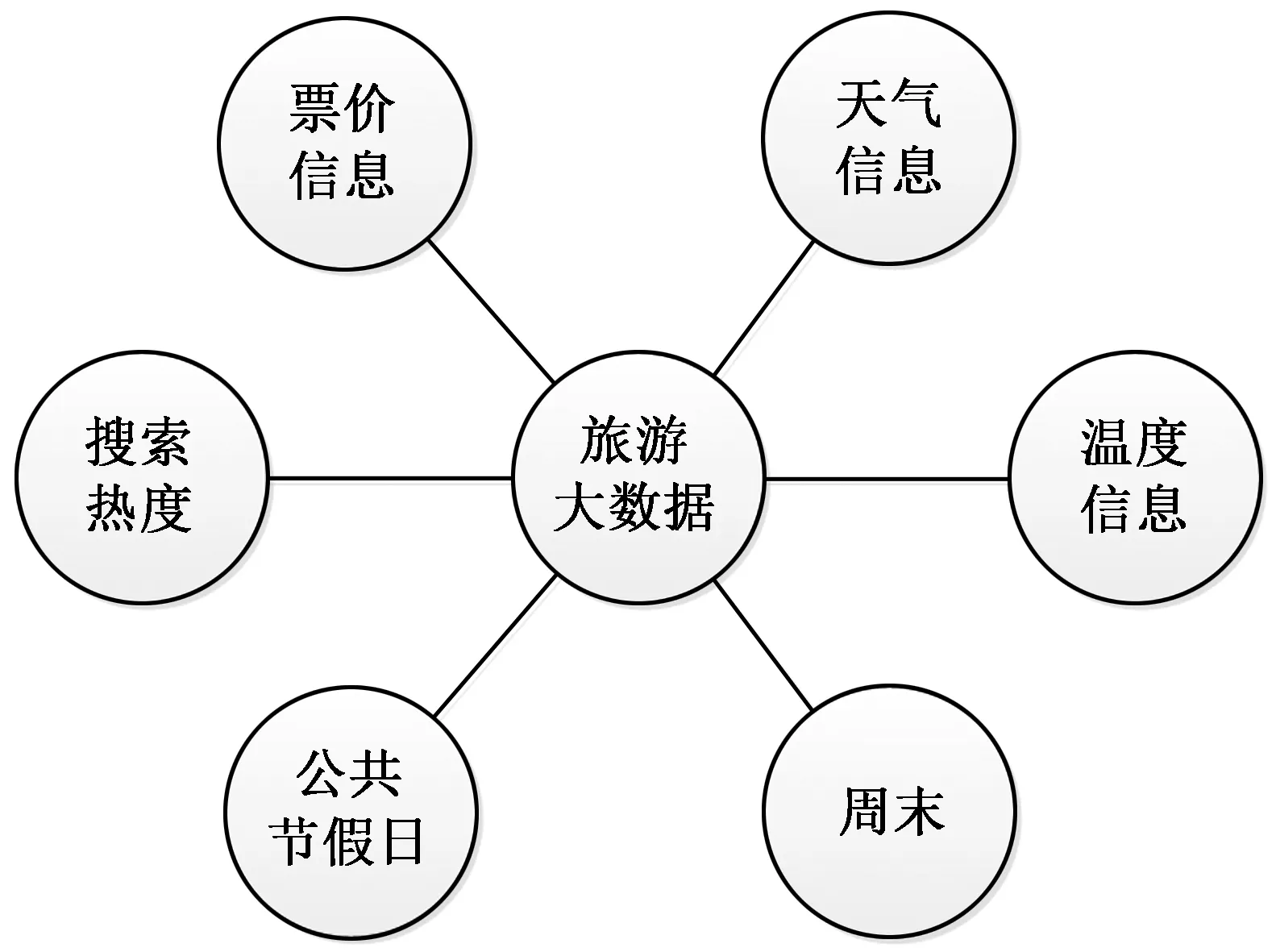
图1 旅游大数据包含的数据源Fig.1 Data sources included in tourism big data

1.2 数据准备

1.2.1变量

令旅游景点每天的售票量为自变量y1，将该景点每天的搜索热度量设为自变量y2。将每日天气设为因变量x1，每日温度设为因变量x2，周末设为因变量x3，公共假日设为因变量x4。同时x1,x2,x3,x4都为外生变量。值得注意的是，评估VAR(p)模型时存在一个现实性问题：尽管希望包含尽可能多的信息，但当引入变量增多时，自由度将会无法满足要求。

1.2.2虚拟变量

由于每日温度因变量x2是数值数据，本文将每日天气x1、周末x3和公共假日x4这些非数值数据设置为虚拟变量，如表1所示。在x1中，0代表良好天气，1代表恶劣天气，其中晴天、多云为良好天气；小雨、阵雨、雷雨、小雪、霜冻、冰冻、大雪等为恶劣天气；在x3中，0代表星期一至星期五的工作日，而1代表星期六至星期天的周末。在x4中，0表示非假日，1表示公共假日。

表1 虚拟变量Tab.1 Dummy variable

2 研究方法

2.1 数据检验

在建模之前应对数据进行检查，避免因数据的不平稳或不均衡造成预测结果不准确。为此，本节采用单位根检验法的扩张的Dickey-Fuller检验(Augmented Dickey-Fuller，ADF)进行时间趋势平稳性检验。ADF检验[7]原理为判断序列是否存在单位根：如果序列平稳，就不存在单位根；否则，就会存在单位根。

传统的VAR模型是针对没有时间趋势的平稳变量设计的，因此非平稳变量不能通过单位根检验，故需要对非平稳变量进行反趋势处理。最经典的去趋势处理方法为Hodrick-Prescott滤波(HP滤波)，可使结果不因时间趋势的存在而产生偏误。

一般情况下，HP滤波可理解为提取趋势变量z=[z1,z2,…,zT]，根据观察到的时间序列o=[o1,o2,…,oT]，求解以下惩罚最小二乘问题：

=(IT+λD′D)-1o

(2)

Δ2zt=Δzt-Δ=zt-2+zt-2

(3)

式中：λ>0为调节参数;IT为大小为T的单位矩阵;D∈R(T-2)×T为二阶差分方程，有Dz∈[Δ2z3,…,Δ2zT]′。

2.2 向量自回归模型

向量自回归模型[8](Vector Autoregressive，VAR)可理解为一个系统方程，其中多个变量被视为内生变量，变量的值根据系统中滞后的因变量进行回归。一般情况下，VAR模型为，

(4)

式中：p是VAR的滞后长度；yt是am向量时间序列的自变量；m是因变量的数量；Yt-j是系统的滞后自变量；k是预定变量的数量；Xt是k个向量的时间序列。

在构建VAR(p)模型时，选择滞后长度是其中最为关键的步骤。一方面，较大的滞后长度值将更好地动态反映模型的特征；另一方面，更大的p值将为模型引入更多的参数。如果一个VAR模型有m个方程，则将有m+pm2个系数被估计，并且一个无限制的VAR模型很可能是过度参数化的，且自由度较低。因此，可以使用Akaike信息准则(AIC)或Schwarz准则(SC)来识别和选择合适的p值。

2.3 Granger因果检验

Granger因果关系[9]可以用来测试一个变量的所有滞后项是否对另一个变量的当前值有影响。如果影响显著，则变量与其他变量之间具有Granger因果关系；如果影响不显著，则变量之间不存在因果关系。格兰杰因果关系的存在表明了变量之间的预测能力。本研究中有两个自变量：每日售出票价y1和每日搜索热度y2。因此，为了探索y1和y2之间的Granger因果关系，应建立如下两个零假设：

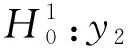
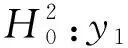
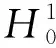
3 案例分析

为了探讨本文所提票价信息、天气、温度、周末、公共节假日和搜索热度6个变量之间的复杂关系，本节以旅游城市重庆为案例验证所提方法的有效性。需注意，本文中所有涉及的数据均来自于网络爬虫。

图2、图3为利用网络爬虫技术搜集的重庆市2019年度温度及天气情况。图4、图5分别为重庆市著名旅游景点票价及热度分布情况。

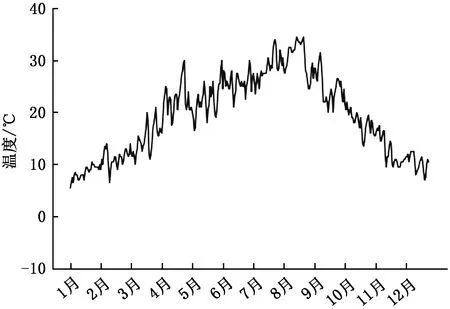
图2 重庆市2019年温度曲线Fig.2 Temperature curve of Chongqing in 2019

接下来，利用ADF方法对各数据进行单位根检验，检验结果如表2所示。其中非平稳变量y1、y2和x2利用反趋势处理，并显示为y1_bias、y2_bias和x2_bias。虚拟变量不必通过单位根检验。可以看出3个变量的时间序列在1%显著水平上都是平稳的，因此其都通过了单位根检验。

利用向量自回归模型及Granger因果检验对数据进行分析。结果表明，当概率水平为0.005时，y1和y2之间存在Granger因果关系(表3)。

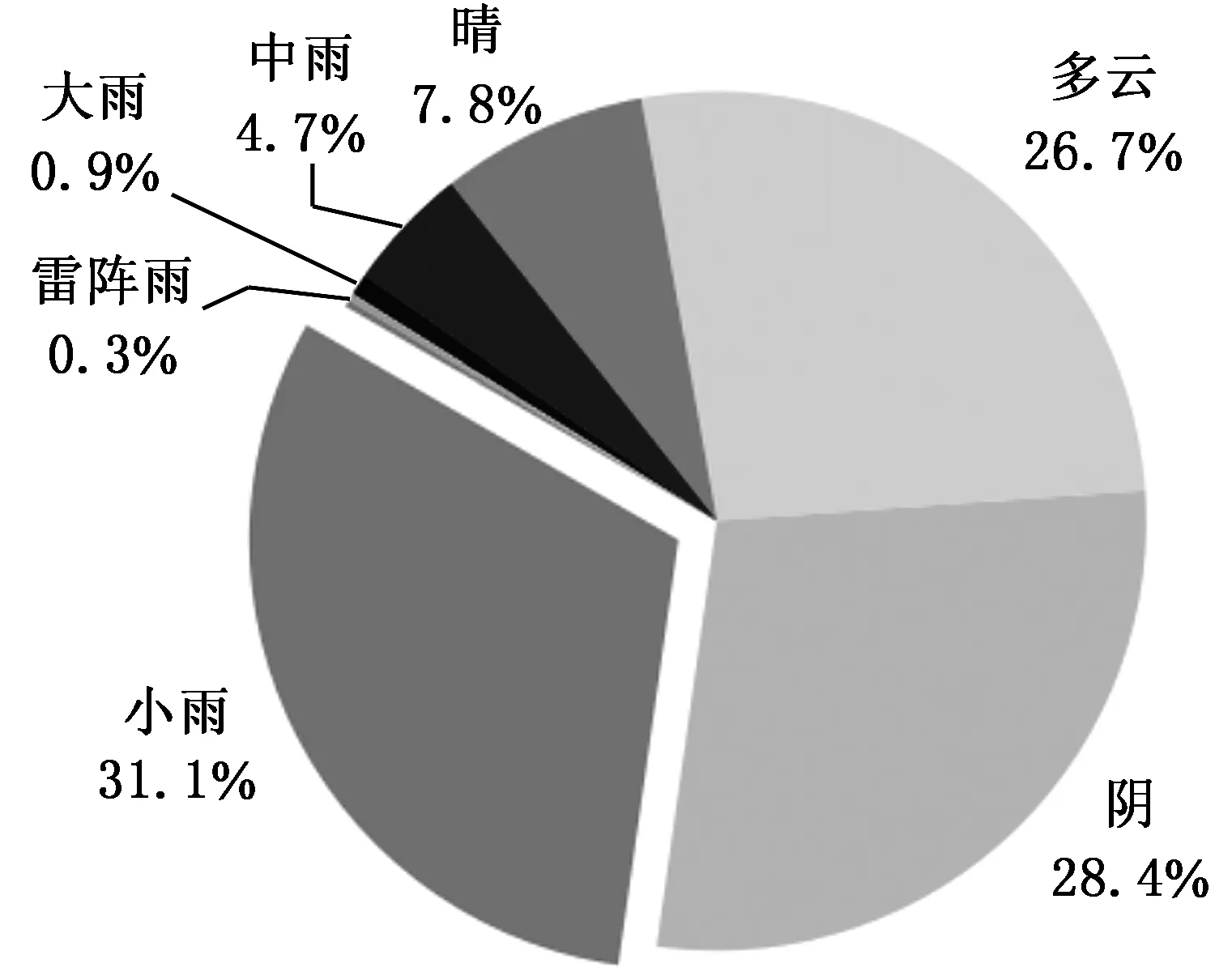
图3 重庆市2019年天气状况Fig.3 Weather conditions of Chongqing in 2019

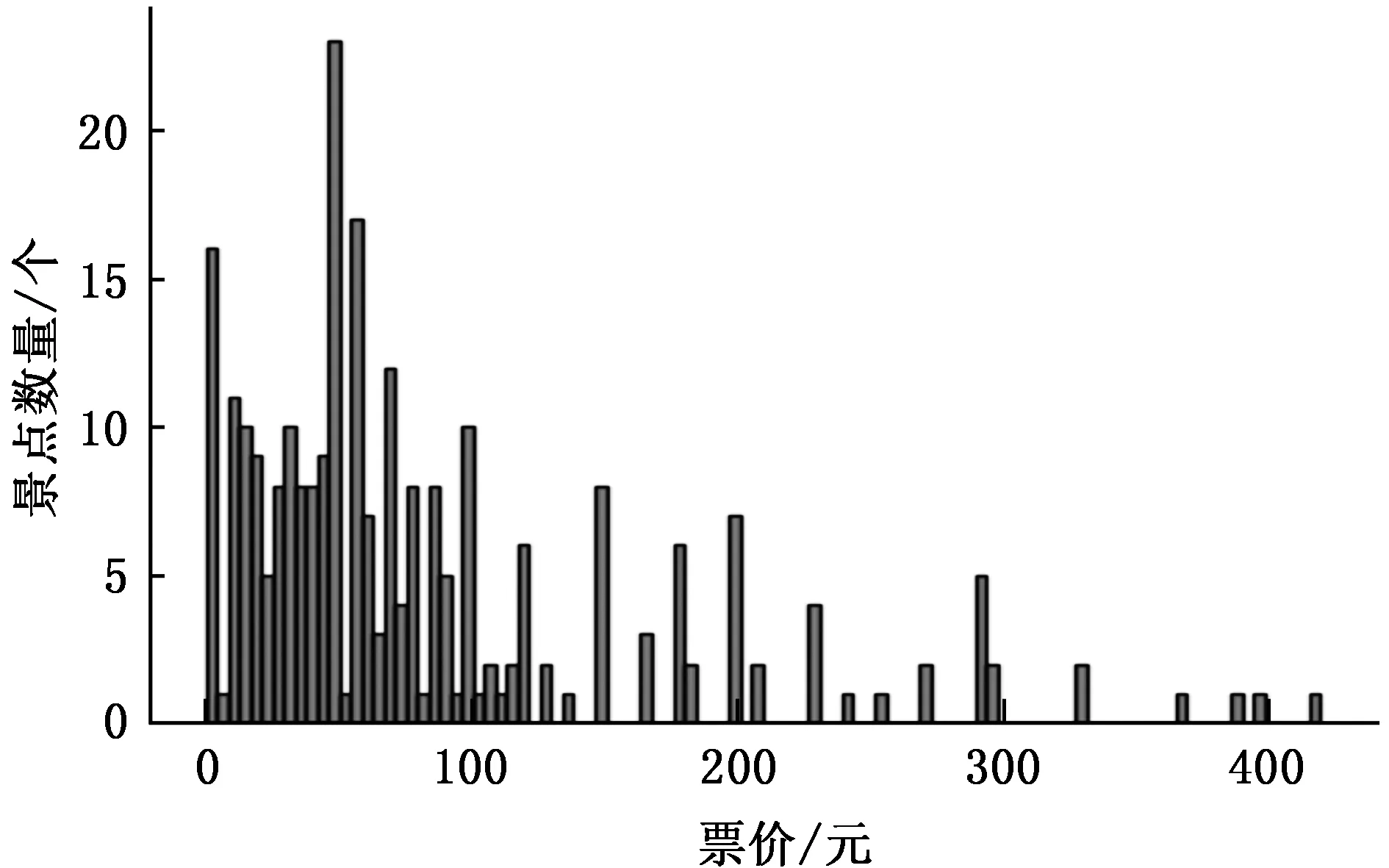
图4 重庆市著名旅游景点票价分布Fig.4 Ticket price distribution of famous tourist attractions

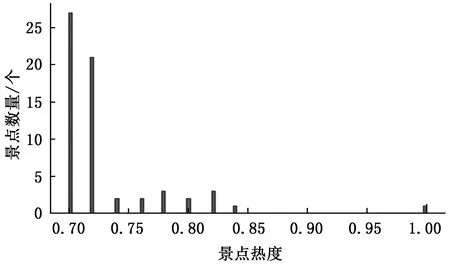
图5 重庆市景点搜索热度分布情况Fig.5 Search heat distribution of tourist attractions

研究结果表明，y1和y2之间存在Granger因果关系；天气与旅游地实际到访人数无关；温度与实际到访人数无相关，但与网络热度呈显著正相关；周末与实际到访人数呈显著正相关，与搜索热度呈显著负相关；公共假日与实际到达人数显著正相关。

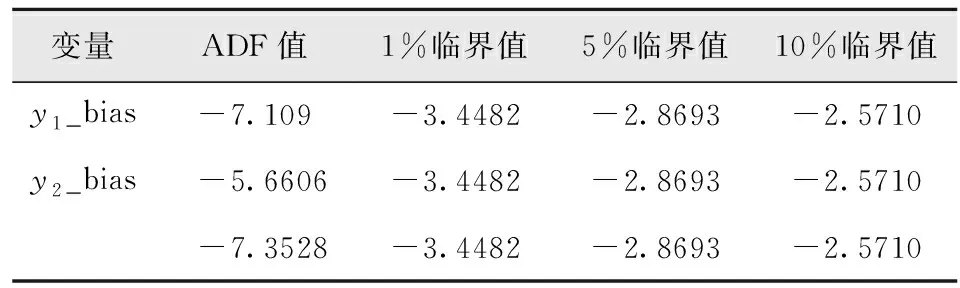
表2 虚拟变量Tab.2 Dummy variable

表3 虚拟变量Tab.3 Dummy variable

4 结语

本文研究了旅游大数据的五维范式，并提出利用ADF法对数据进行时间趋势平稳性检验。最后，建立向量自回归模型探索票价信息、天气、温度、周末、公共节假日和搜索热度6个变量之间的复杂关系。