建构思维模型,进行初中化学溶液的综合计算的教学
刘庆华

摘要:针对初中化学溶液的综合计算的教学中忽略知识之间的关联性、系统性,盲目进行机械训练的应试教学现状,探讨通过呈现问题、追根溯源、流程导图等分析推理,解决学生综合计算的学习困难。数据对比表明,建构思维模型,进行初中化学计算的教学,增进了学生的计算理解、发展了学生的深度思维、增强了学生问题解决的能力。
关键词:综合计算;模型建构;教学策略
文章编号:1008-0546(2022)06x-0012-05 中图分类号:G632.41 文献标识码: B
doi:10.3969/j.issn.1008-0546.2022.06x.003
化学计算是初中化学教学的重要组成部分,是学生理解、巩固、应用知识的基本途径,是形成技能、发展智力、培养能力的重要手段[1]。初中化学计算的类型包括化学式计算、化合价计算、化学方程式计算、含杂问题的计算、溶液的有关计算以及利用质量守恒定律的计算等。而溶液的综合计算则往往是由以上几个简单化学基本计算融合而成,具有综合性强、思维容量大等特点,能全面考查学生的逻辑推理、综合分析能力,真正达到考知识、考能力、考素养的要求,是天津市历年中考必考题,分值为6分。天津市滨海新区近几年的中考数据显示:学生溶液的综合计算的得分率在60%左右,远低于整套试卷的平均得分率。为此,笔者对天津市滨海新区初中化學溶液的综合计算的教学现状进行了调查分析,针对教学中出现的问题,回归化学计算的本质,用数学的方法处理物质的性质和变化规律,通过证据推理对变化中蕴含的定量关系进行模型建构。
一、溶液的综合计算教学现状分析
溶液中溶质的质量分数计算是初中化学的重要内容,包括单一溶液中溶质的质量分数、溶液的稀释、化学反应后溶液中溶质的质量分数等问题。后者是化学反应、化学方程式、质量守恒定律、溶液、溶质的质量分数等多方面知识的综合,可称之为涉及化学反应的溶液的综合计算[2],本文简称为溶液的综合计算。
1.教师层面
通过多次下校听课、教师访谈、学科教研可以发现,多数教师在进行溶液的综合计算教学中采取了相似的教学方法和教学思路:
(1)例题讲解——根据问题逆推,通过公式引领进行相关数据的代入和求解,提醒学生注意双溶质问题。
(2)重点突破——利用质量守恒定律计算反应前或反应后溶液的质量,总结公式m(溶液,后)=m(所有,前)-m(非溶液,后)。
(3)反复操练——针对各种不同信息条件的习题进行强化练习。
2.学生层面
在调查中,对学生的课堂表现和练习中暴露的问题进行了汇总:
(1)基础较差的学生看到题目信息复杂,因读不懂题意就望而却步根本不做。
(2)中等生能够模仿教师的解题步骤,但并不能完全理解题目中的物质转化关系,因此当题目信息稍做变化时就不知所措。
(3)领悟力较强的优等生能够理清题目中的各种物质关系,形成解题思路,但往往因为忽略一些细节信息而出错。
究其原因,其中一个重要的方面是在综合计算的教学中,教师往往把着眼点放在对所求问题的局部分析和计算难点的局部突破,而非站在学科的整体性角度系统地分析各部分知识之间的内在联系,建构模型,进行举一反三的应用。这种忽略知识之间的关联性、系统性的应试教学方法常常会“欲速则不达”,使学生“只见树木不见森林”,很难真正提高学生的综合能力。另外,在一些教师的教学过程中,往往只把“化学综合计算”作为一项基本技能,过于程式化,片面强调对做题步骤的模仿和反复练习,结果学生熟记概念、死套公式,只是一种暂时性熟练,对学科概念、反应原理的本质及其表征不能深刻理解,更不能让学生习得解题能力。“解题”并不等于“做题”,在字典中“解”的含义是“领会、觉悟”,而“做”只是简单地“从事某种工作或活动”。因此,为了使学生真正领悟化学综合计算题中各部分知识之间关联性,形成清晰的解题思路,就需要教师引导学生站在学科的角度进行基于原点的模型建构。具体地说,就是根据一定的线索和中心点,将相关的知识按一定秩序串联起来,形成知识整体和系统,建立起基于整体认知的综合计算模型,并引导学生从整体角度去分析各知识点的地位及相互关系,从而揭示事物的本质和规律。
二、溶液的综合计算内容的整体分析
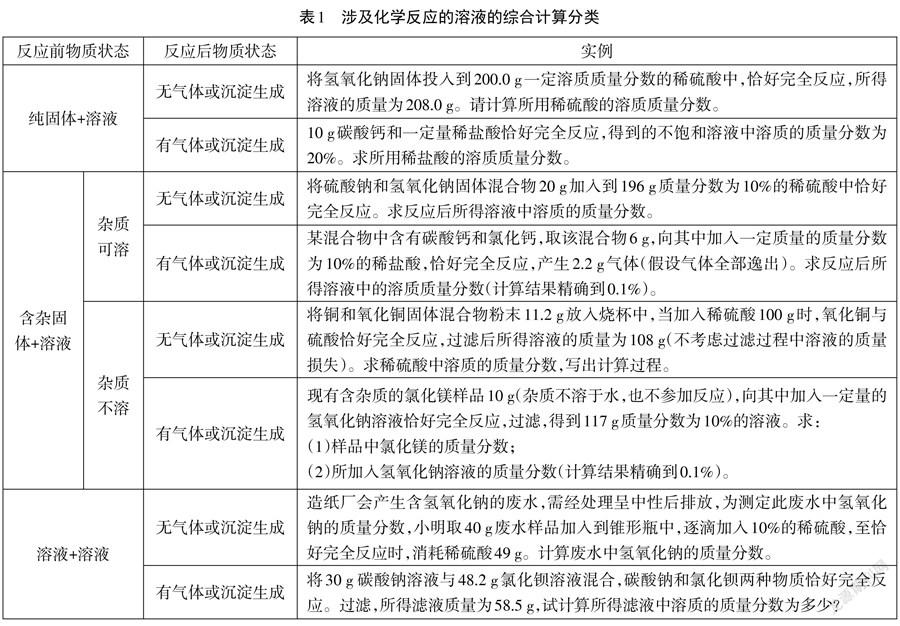
根据课标要求,分析近年来中考初中化学溶液的综合计算的试题形式,一般是以化学方程式计算为基础,并结合溶质质量分数计算。该类化学综合计算中的化学反应类型主要涉及有溶液参加的置换反应和复分解反应,依据反应前后物质的存在状态,可以进行如下分类(见表1)。
通过表1可以看出,溶液的综合计算以化学方程式为基础,通过情境设置和问题变换会出现多种不同的类型。其中,反应前物质的状态设置往往通过固体含杂质提升难度,若杂质可溶通常需考虑反应后的双溶质问题;若杂质不溶需注意反应后溶液的质量不包含杂质。反应后物质的状态会通过产物中有气体或沉淀生成提升难度,若气体或沉淀质量直接给出则可以直接用在化学方程式中进行计算;若气体或沉淀质量没有直接给出,则需要比较反应前后质量的变化间接求得。难度设置一般是求溶质的质量分数时溶液的质量未知,需要通过质量守恒定律求得。
三、溶液的综合计算思维模型的建构
溶液的综合计算,不管条件如何变换,教师都需要引导学生从“定性”和“定量”的角度分析题中所发生的化学反应,通过分析、推理认识其本质特征、构成要素及相互关系,建立模型,运用模型揭示综合计算的本质和规律,其思维模型见图1[3]。
四、溶液的综合计算教学目标
基于上述分析,确立溶液的综合计算的整体性教学目标如下:
1.通过简单化学计算到化学综合计算的演变过程,从起点上领会化学综合计算题的解题根源和解题方向。ED3976A7-A084-4833-B060-39C7AFDEAD57
2.通过将化学综合计算题的文字信息转化为信息导图,从结构上直观地把握各物质之间的转化关系。
3.通过归纳总结化学综合计算题解题关键点,从整体上形成清晰地解题思路。
五、溶液的综合计算教学策略
教学目标的达成需要借助相应的有针对性的教学策略来实现,以天津市一道中考题为样题介绍化学综合计算建模教学的主要策略。
例题.:纯碱样品中含有少量的氯化钠,某同学为测定该纯碱样品中碳酸钠的含量,他取该纯碱样品11 g,全部溶解在100 g 水中,再加入150.7 g 氯化钡溶液,恰好完全反应,过滤,得到19.7 g沉淀(不考虑过程中物质质量的损失)。请计算:(1)纯碱样品中碳酸钠的质量;(2)所加氯化钡溶液的溶质质量分数(结果保留到0.1%);(3)反应后所得溶液中溶质的质量分数。
例题属于含杂质固体与溶液反应,杂质可溶,生成物中有沉淀生成的类型。题中直接给出沉淀质量可以用于化学方程式中进行计算,反应后的溶质需考虑双溶质问题,溶液的质量需通过质量守恒定律间接求出。
1.追根溯源——整体把握解题方向
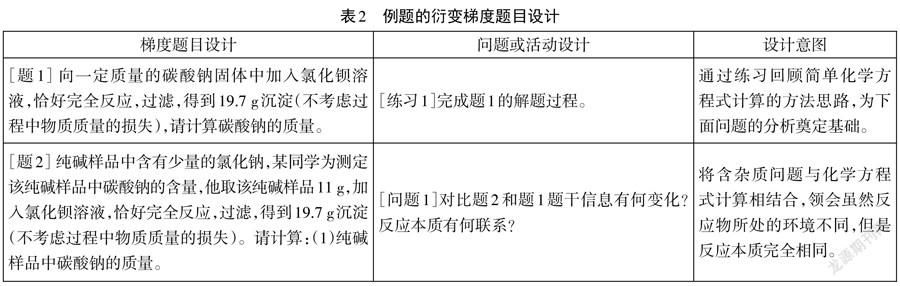
通过对历年天津市中考最后一题“化学综合计算题”的对比分析,不难发现:化学综合计算题虽然表面上题目复杂、高深莫测,但实际上都是以简单的化学方程式计算为基础,将其他计算类型(如:溶液的有关计算、含杂质问题计算、质量守恒定律等)融入其中而形成。因此,在教学中,教师可以带领学生分析出综合计算是如何从一道简单的化学方程式计算发展演变而来的,体验解化学综合计算的根源,以及各种简单计算的融合方式。例题的衍变梯度题目设计如表2所示。
(1)对比变式,寻根源
题1是简单的化学方程式计算,题目中发生的化学反应方程式为: Na2CO3+BaCl22 NaCl+BaCO3↓,已知沉淀 BaCO3的质量求反应物 Na2CO3的质量。而在题2中则将Na2CO3设计为含有NaCl杂质的纯碱样品,在化学方程式计算中融入了含杂质问题,虽然题干信息好像复杂了很多,但分析所发生的化学反应,杂质 NaCl并不参与 Na2CO3和 BaCl2的反应,因此题1与题2本质上是完全相同的。通过这样的变式对比,可以让学生深刻领悟到:不管题干信息如何变换,解题的根源都在于发生的化学反应。
(2)立足根源,促发展
根据化学方程式中某一物质的质量,我们可以计算出化学方程式中其他任一物质的质量。对比题3和题2,已知的信息增加了 BaCl2溶液的质量,所求的问题也指向了对 BaCl2溶液中溶质质量分数的求解,表面上看与题2没有多大的联系,但实质上反应的本质并没有改变,只是将计算的目标由 Na2CO3转向了另一反应物 BaCl2,然后再与溶液的有关计算相结合求出溶质的质量分数。由此可见,简单的化学方程式计算是化学综合计算的基础,化学综合计算往往是以发生的化学反应方程式为根源,然后在不同的目标物质上发展延伸融入其它的化学计算。
(3)变化发展,找规律
对比题4和题3,有很多的相似之处,也是在原有化学反应的基础上变换了计算的目标物质,同时与溶液的有关计算相结合。不同的是:题4与题3相比进一步延伸加大难度,目标物质 NaCl 的来源有两部分(原纯碱样品中的和反应生成的);反应后溶液的质量没有直接给出,需要通过质量守恒定律计算。学生通过问题4中简单的条件转换,可以根据题干信息的不同,巧用质量守恒定律。
2.流程导图——整体把握解题细节
为了将复杂的、抽象的问题简单化、直观化,我们在教学中往往会采用一些图示的方法。例题的实验信息如图2所示。该图示能够比较直观地展示题干信息中的实验过程,但是不能清楚说明物质之间的转化关系和质量变化关系,不利于学生从整体上把握反应的本质和解题的细节。
为了更加系统清晰的显示出化学综合计算题干信息中隐含的物质间的内在联系,我们可以采用信息导图的形式。例题的信息导图如图3所示。该图不但提炼出了题干中涉及的重要物质和数据,而且进一步显示了物质间的相互转化关系和存在形式,是在对化学基本概念、原理理解的基础上进行的化学量化分析過程,有利于学生从整体上理解题意、把握解题的每一个细节,同时也有利于突破化学综合计算的难点—双溶质问题和质量守恒定律的应用。
3.五步战略——整体把握解题思路
解题思路的模型建构是提升学生解题能力的关键。在化学综合计算的教学中,我们可以通过以下五步战略引导学生形成整体的解题思路:绘制流程图→立足方程式→找准纯质量→发现生长点→巧用守恒法。绘制流程图是对题干信息的提炼和整体分析,是解题的前提和保证;立足方程式是对各物质内在联系的整体把握,是解题的根源和基础;找准纯质量是基于化学方程式计算的入手点和突破口;发现生长点是对不同化学计算类型融合方式的整体认知,是以化学方程式为基础在不同目标物质上进行的延伸和发展;巧用守恒法是突破化学综合计算难点的关键。我们可以把化学综合计算题比作一盆生长茂盛的花朵,题中所发生的化学反应是花的根,不同的条件信息和问题设置是在不同的节点开出的一朵朵美丽的花朵,如图4所示。
六、调查与反思
笔者以2021届滨海新区大港六中九年级八班的学生为研究对象,将建构思维模型的溶液的综合计算应用于教学实践中。通过课后的学生访谈了解到:大多数学生感觉溶液的综合计算不像原来想象的那么难了;基础差的学生不再逃避,而是通过流程导图对题目进行认真分析,找到了解题的根源;中上等的学生能够从整体上理解题意并形成清晰的解题思路,信息导图使他们的分析更有针对性、更细致。2021年天津中考第26题的检测结果显示:几乎所有的同学都会根据题干信息进行提炼分析,绘制出信息导图;全班该题的得分率72%,比2020年天津市滨海新区该题得分率高出11%。
在语文和英语的教学中常常强调整体解读文意[4],化学教学也需要从整体角度引导学生分析各知识点的地位及相互关系,从而揭示事物的本质和规律。溶液的综合计算解题应该做到:综合问题——精细拆分求破解;定量思考——计算本质是比例;模型建构——深度思维是关键。让学生从整体上把握解题的方向、解题的细节和解题的思路,才能使学生领悟物质间转化的内在联系,真正提高解题能力。
参考文献
[1]赵王荣桥.一题多变举一反三融会贯通培养能力.中学化学教学参考,2014(5):56-57.
[2]卫冰洁,何彩霞,杨艳红.用可视化分析过程理清解决问题的思路——以初中化学“涉及化学反应的溶液综合计算”复习课为例.教学仪器与实验,2014(12):3-7.
[3]罗月旺.培育证据推理与模型认知素养的初中化学计算教学.化学教学,2018(7):51-54.
[4]朱琳.高中英语课文篇章整体分析教学法.考试周刊,2008(11):131-132.ED3976A7-A084-4833-B060-39C7AFDEAD57

