基于长短期记忆网络和Logistic回归的重症监护病房脑卒中患者院内死亡风险预测
邓宇含,姜 勇,王子尧,刘 爽,汪雨欣,刘宝花△
[1.北京大学公共卫生学院社会医学与健康教育学系,北京 100191;2.国家神经系统疾病临床医学研究中心,首都医科大学附属北京天坛医院神经病学中心,北京 100050;3.北京大数据精准医疗高精尖创新中心(北京航空航天大学&首都医科大学),北京 100070]
脑卒中是全球最主要的死亡原因和致残原因之一[1],给社会带来严重经济负担[2]。尽管脑卒中患者的死亡风险在西欧和北美的大多数国家中都呈下降趋势[3],但在需要进入重症监护病房(intensive care unit,ICU)治疗的患者中死亡风险仍然较高[4]。如果能对死亡风险高的患者进行早期识别,在患者病情恶化前预警并采取有针对性的预防和治疗措施,则对于医疗资源的合理分配以及降低患者死亡风险和改善患者预后方面都具有重要意义[5]。
ICU内获取的数据与常规数据的区别在于其大多为时序数据,即对同一变量在不同时间进行了多次测量[6]。目前用于时序数据处理的模型主要为循环神经网络(recurrent neutral network, RNN)等深度学习模型,这些模型由于能够从大样本、高维数据中学习变量间复杂的交互作用而不需要遵从统计学假设[7],从而在放射[8]、肿瘤[9]、重症监护[10]等医学领域有了越来越多的应用。然而,RNN在实际应用时存在诸多弊端,例如其无法对长期信息进行学习,因此在时序数据的处理方面存在一定的局限性。
长短期记忆网络(long short-term memory, LSTM)[11]在RNN的基础上增加了门控单元,从而可以对时序信息进行选择性遗忘或保留,因此具有较好的预测效果,被较多地应用于ICU内,如Thorsen-Meyer等[12]使用动态的LSTM模型对患者进入ICU后90 d内的死亡风险进行了实时预测,Xia等[13]使用LSTM集成算法对ICU患者28 d内的死亡风险进行了预测,Maheshwari等[14]用LSTM模型预测了ICU内心血管疾病患者的死亡风险。然而,LSTM等深度学习模型由于内部结构复杂,无法判断特定变量对结局的具体贡献,因此可解释性较差[15]。
Logistic回归作为传统的统计学模型,其优势在于可以对变量和结局间的关系进行很好地解释,但由于其要求变量间不存在共线性等较为严苛的应用条件使其在实际应用时受到限制[16]。如果将深度学习模型和Logistic回归相结合,使二者优势互补,对于疾病预测或许会具有很大价值。
本研究以重症医学信息数据库(Medical Information Mart for Intensive Care-Ⅳ,MIMIC-Ⅳ)为数据源,基于引入注意力机制的LSTM深度学习模型和L1正则化的Logistic回归提取脑卒中患者进入ICU后48 h内的重要变量,再用传统的Logistic回归构建脑卒中患者死亡风险预测模型,对模型的预测效果进行评价,并与未预先进行变量筛选而直接进行前进法Logistic回归的模型进行对比。
1 资料与方法
1.1 研究对象
研究对象均来源于MIMIC-Ⅳ数据库,该数据库由美国麻省理工学院(Massachusetts Institute of Technology, MIT)计算生理学实验室和贝斯以色列迪康医学中心(Beth Israel Deaconess Medical Center, BIDMC)提供,包含了2008—2019年期间ICU或急诊科收治的256 878位患者的真实住院信息。MIMIC-Ⅳ数据库由核心模块、住院模块和重症监护模块三个模块构成,包括了患者基本信息、诊断编码、实验室检查、生命体征、药物处方、手术类型等较全面的临床信息记录,并对所有患者信息均进行了去识别处理。
本研究选取MIMIC-Ⅳ数据库中出院诊断为脑卒中的2 755位患者作为研究对象,纳入流程图见图1。纳入标准:年龄≥18岁;经国际疾病分类(International Classification of Diseases,ICD)第9版(ICD-9)或第10版(ICD-10)诊断标准确定的首要诊断为脑卒中的患者。排除标准:无ICU入院记录的患者;入院后48 h内出现院内死亡或出院的患者。对于有多次ICU入院记录的患者,所有ICU记录均纳入统计分析。

MIMIC-Ⅳ, Medical Information Mart for Intensive Care-Ⅳ; ICU, intensive care unit.
1.2 预测变量和结局指标
以入院48 h后是否出现院内死亡为结局指标。结合既往研究结果[17-18]、脑卒中诊治指南及MIMIC-Ⅳ数据库特征,纳入以下变量作为预测变量:人口学特征(性别、种族、年龄、卒中类型)、生命体征(收缩压、舒张压、平均血压、体温、心率、呼吸频率、血氧饱和度)、实验室检查(白细胞计数、血红蛋白、血小板、肌酐、尿素氮、钠离子、钾离子、葡萄糖、氯离子、碳酸氢盐、总胆红素、凝血酶原时间、白蛋白、血细胞比容、红细胞分布宽度、阴离子间隙、pH值、国际标准化比值、乳酸)、合并症(高血压、高脂血症、糖尿病、充血性心力衰竭、心房颤动、周围血管病、肾脏疾病、肝脏疾病、呼吸衰竭、慢性阻塞性肺疾病),其中,生命体征和实验室检查数据均为重复测量数据。
1.3 引入注意力机制的LSTM模型
LSTM在RNN的基础上增加了门控单元,从而对当前状态和过去状态的信息进行选择性遗忘或保留。RNN处理时间序列数据的机制为通过隐藏层对时序信息进行保留和传递,可表示为:Ht=φ(WhhHt-1+WhxXt+bh),Ot=tanh(WhoHt+bo),其中,Xt为当前时点的变量值,W为权重,b为偏移,Ht-1为上一个时点的隐藏状态,当前时点的隐藏状态Ht是由当前时点的输入变量Xt和上一个时点的隐藏状态Ht-1共同决定的,下一个时点的隐藏状态Ht+1又由下一个时点的输入变量Xt+1和当前时点的隐藏状态Ht共同决定,即每一个隐藏状态都包含了此前所有时间步的信息。


LSTM, long short-term memory.It, input gate; Ft, forget gate; Ot, output gate; candidate memory cell; Ct, memory cell; Ht, hidden layer; Xt, input variables; Ct-1, memory cell at last time step; Ht-1, hidden layer at last time step.
由于LSTM内部结构复杂,无法得出变量对结局的具体贡献并进行合理的解释,为增强模型的可解释性,在变量输入的水平上引入了注意力机制,即在变量进入LSTM之前,给予在各时点测量的每个变量一定的注意力权重at,在每个时点,所有变量注意力权重at之和为1,at可以表示为:at=softmax(xtWt)。此时,新的输入变量为:Xnew=A⊙X。通过对各时点的整合可以得到每个变量对结局的全局贡献,从而进行变量筛选。
本研究中LSTM的超参数在模型训练前根据既往研究结果[20]预先确定,再根据验证集上的受试者工作特征曲线下面积(area under curve, AUC)进行调整。最终采用的超参数为:unit为128的单层LSTM,Sigmoid激活函数,dropout为20%,通过RMSPROP优化器进行训练,学习率0.001,rho为0.9,episilon为1e-08,迭代次数为10次,批样本量为64。
1.4 L1正则化的Logistic回归模型

1.5 时序数据处理
由于生命体征变量多以小时为单位进行测量,因此以小时为单位对入院后的48 h进行划分,并对每小时的各指标进行记录,即划分后每位患者均存在48个时间点×39个变量的二维数据。为使每个时点对应唯一的变量值,若某变量在1 h内被多次测量,则取该小时内测量值的均值作为该时间点的变量值,若某变量在某时点存在缺失,则采用末次观察推进法(last observation carried forward,LOCF)对该时点的缺失值进行填补。对于年龄、性别、出院诊断等非重复测量数据,48个时间点均记录相同值。去除初次填补后缺失比例大于30%的变量,其余连续变量的缺失值用均值填补,分类变量的缺失值用出现比例较高的哑变量填补。LSTM模型对48 h内每个时点的所有数据均进行了提取和利用,而在L1正则化的Logistic回归模型中,48 h内的重复测量数据以最大值、最小值、均值和标准差的形式表示后纳入模型。
1.6 统计学分析
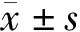
2 结果
2.1 基本信息
共纳入2 755位脑卒中患者,共包含2 979条ICU入院记录,其中526条入院记录存在对应的院内死亡记录,占17.66%。患者基本情况、实验室检查、生命体征检查和合并症的组间比较见表1。对于重复测量数据,取48 h的均值进行组间比较,其中,除性别、卒中亚型、慢性阻塞性肺疾病、血脂异常、周围血管病变、收缩压外,其余变量在是否出现院内死亡上的差异均有统计学意义(P<0.05)。

表1 根据院内死亡情况分组的ICU脑卒中患者的变量特征
2.2 变量筛选模型的预测效果
LSTM模型和L1正则的Logistic回归模型在10次随机划分数据集中测试集的AUC分别为0.760±0.018和0.819±0.031,经配对t检验比较两者差异有统计学意义(P<0.001),测试集的受试者工作特征曲线见图3。
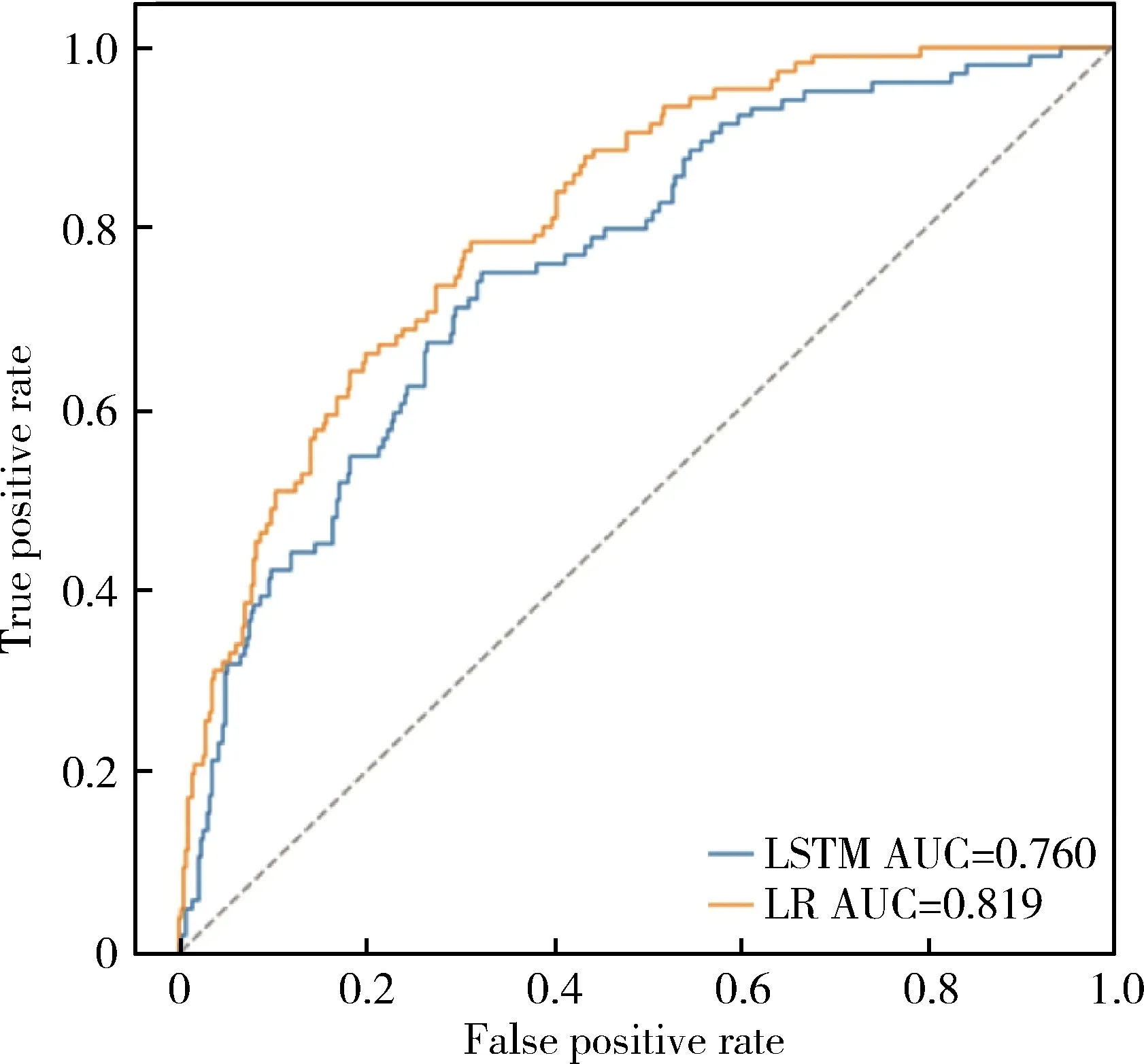
LSTM, long short-term memory; LR, Logistic regression; AUC, area under curve.
2.3 变量重要程度
经LSTM模型得出的变量重要程度中排名前20的变量见图4。前10的变量依次为血糖、呼级衰竭、年龄、尿素氮、种族(白种人)、充血性心力衰竭、肝脏疾病、高脂血症、碳酸氢盐浓度、糖尿病。通过L1正则的Logistic回归得出的经最大值、最小值、均值和标准差扩充后变量的回归系数见图5,回归系数绝对值位于前10的变量分别为心率均值、年龄、心率最小值、钠离子浓度最大值、血糖均值、钠离子浓度标准差、尿素氮标准差、血红蛋白标准差、血氧饱和度均值和阴离子间隙均值。

LSTM, long short-term memory; CHF, congestive heart failure; AFIB, atrial fibrillation; WBC, white blood cells; RDW, red cell volume distribution width.

HR, heart rate; WBC, white blood cells; RR, respiratory rate; PT, prothrombin time; SD, standard deviation.
2.4 预测模型的建立与比较
选取两个模型所得出的重要程度排名前10的变量,通过主成分法对连续型变量进行聚类,通过1-R2统计量在每个类内选取唯一变量以去除变量间的共线性。对二分类变量进行相关性分析,对存在较强相关性的变量仅保留其中之一进入Logistic回归模型,最终得到的预测模型见表2。模型共纳入15个变量,测试集AUC为0.851,最佳截断值下,灵敏度为85.98%,特异度为71.74%,预测准确率为74.26%。

表2 基于Logistic回归的预测模型
为比较模型的预测效果,将未进行变量筛选的所有变量,即以最大值、最小值、均值和标准差的形式表示的重复测量的变量以及其他未经处理的非重复测量变量(共102个变量)纳入Logistic回归模型,分别用前进法、后退法和逐步法筛选变量并建立预测模型。其中,前进法模型效果最好,模型共包含26个变量,测试集AUC为0.827,最佳截断值下,灵敏度为73.83%,特异度为79.16%,预测准确率为78.22%。两种预测模型的受试者工作特征曲线见图6。
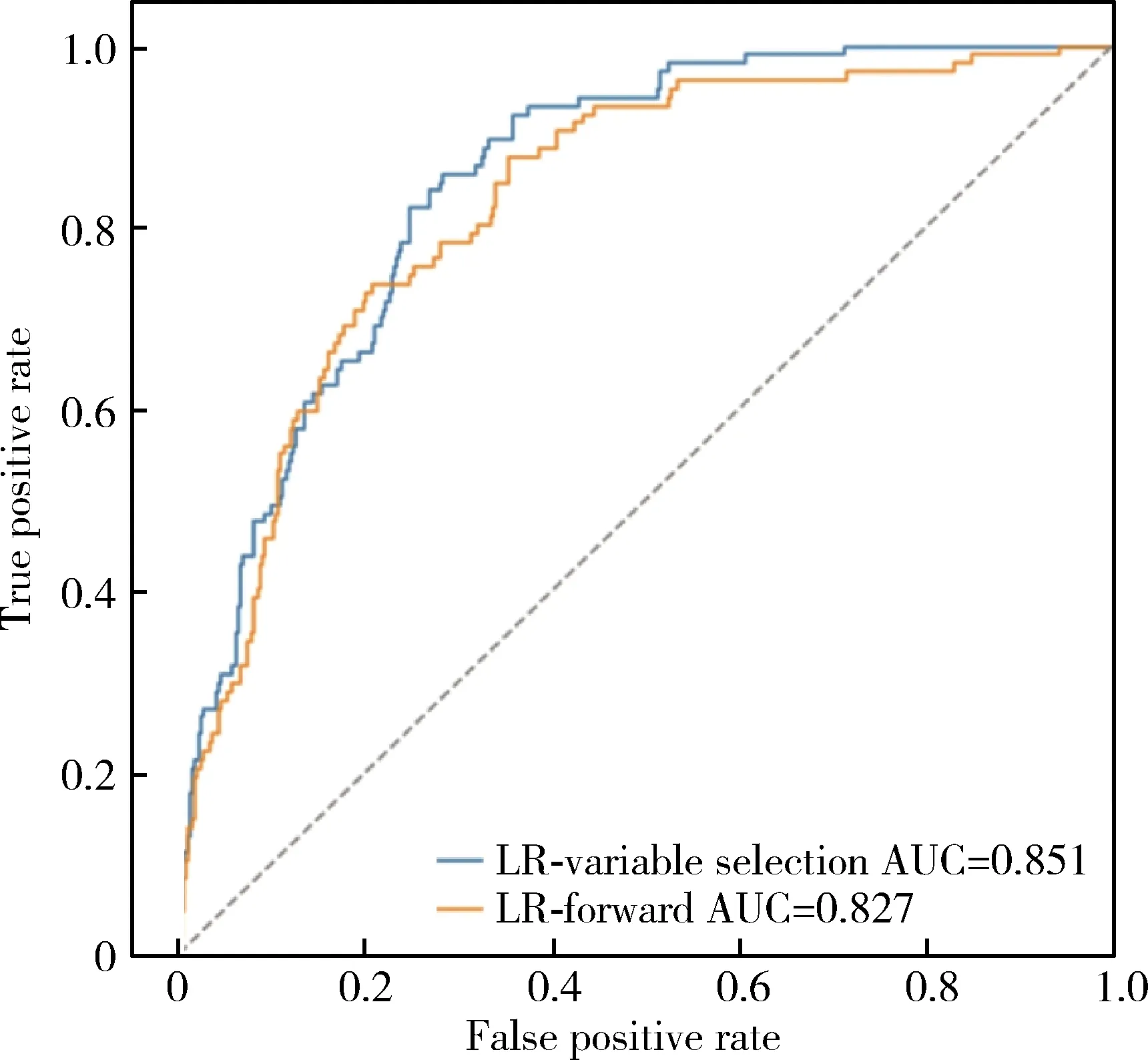
LR, Logistic regression; AUC, area under curve.
3 讨论
脑卒中患者是否出现院内死亡受多种复杂因素的影响。本研究通过既往研究结果[17-18]、临床经验以及MIMIC-Ⅳ数据特征,纳入了包括心率、呼吸频率、血氧饱和度等在内的潜在影响因素,通过引入注意力机制的LSTM深度学习模型和L1正则化的Logistic回归对变量进行筛选,将重要程度最高的15个变量纳入Logistic回归模型,通过AUC等指标评价模型效果,达到使用尽可能少的变量对死亡风险进行相对准确预测的效果,从而辅助临床决策。
ICU内收集的数据与其他数据的区别在于其多为重复测量数据,传统的统计学模型和机器学习模型倾向于将重复测量数据以少数独立的综合指标概括后进行模型建立,而这样并不能将时序数据中所包含的信息充分提取出来,可能导致有偏倚的结果[21]。LSTM模型由于可以对时序数据进行学习[22],因此对于数据信息的利用较为充分,然而,从两种变量筛选模型的预测效果来看,LSTM的预测效果并没有L1正则化的Logistic回归预测效果好,出现这种结果的原因可能是由于本研究纳入的生命体征等测量频率较高的时序数据较少,而纳入较多的实验室检查数据的测量频率并不高,从而影响LSTM对长期依赖关系进行学习[23]。通过最大值、最小值、标准差和均数等指标,可以将时序数据的集中趋势和离散程度的信息较充分地表现出来,可能造成L1正则化的Logistic回归在预测效果方面表现更好。在变量进入LSTM之前,通过注意力机制对变量赋予一定的权重,从而增强模型的可解释性,然而,与L1正则化的Logistic回归相比,注意力机制产生的变量重要性仅能提供变量的重要程度的结果,而对于变量对结局影响的方向信息无从获取。L1正则化的Logistic回归虽然可以通过偏回归系数得到变量对结局影响的方向和程度,但由于该模型无法利用原始数据信息,即时序数据信息,而仅能将由时序数据转化而来的综合指标信息作为输入,因此对于筛选后所得变量的完整性和综合性方面表现较差。例如,对于尿素氮这一指标,两个变量筛选模型均将其列为重要程度排名前10的变量,但L1正则化的Logistic回归所提取出的仅是尿素氮的标准差这一指标,而这一指标无法对原始数据的信息进行充分囊括,且不具备较为明确的临床意义。
从两种模型筛选出的变量来看,年龄、血糖和尿素氮在两个模型中都是重要程度位于前10的变量,其中,年龄与脑卒中预后的关系在既往研究中也已被证实,即年龄是脑卒中结局最重要的预测因子之一[24-26]。这与本研究建立的预测模型中的结果相一致,即年龄的OR值为30.81所表明的年龄与脑卒中死亡风险之间有极强关联。年龄越大的患者,身体机能相对越差,合并的慢性病也越多,因此发生不良预后的风险越高。此外,本研究得出血糖与脑卒中的预后有重要关系,这也与既往研究结果一致[27]。持续性血糖升高与预后不良显著相关[28],血糖对脑卒中预后的影响涉及包括内皮细胞功能受损、一氧化氮生成紊乱[29]和血管收缩因子激活[30]等在内的复杂神经病理学机制,最终表现为血管收缩、炎症、血栓等不良反应[31]。本研究结果显示,尿素氮与脑卒中患者的院内死亡风险相关,既往研究也得出了相同结果[32]。
由于两种模型是基于不同原理进行变量筛选,因此得出的重要变量存在差异,其中,LSTM倾向于筛选出合并症相关变量,而L1正则化的Logistic回归则倾向于筛选出生命体征和实验室检查相关变量,这一方面是由于生命体征和实验室检查等重复测量数据在L1正则化的Logistic回归里被扩充为最大值、最小值、均值和标准差的形式,即每个重复测量的变量个数都在原先的基础上被扩大了4倍,而合并症等变量个数并没有发生改变,因此生命体征和实验室检查变量被筛选为重要变量的机会更大。
从最终建立的Logistic回归模型的预测效果来看,相比于未预先用深度学习(LSTM)和机器学习(L1正则化的Logistic回归)方法进行变量筛选而直接通过前进法Logistic回归建立的模型,经过深度学习和机器学习方法进行变量筛选后再用Logistic回归建模具有明显的优势,表现在其用远少于前进法Logistic回归的变量数得到了优于前进法Logistic回归的预测效果。进行变量筛选的目的在于提高预测效果,在一定程度上筛选出高危人群并在实际应用时节省开销[33]。本研究采用两种不同的方法充分利用时序数据信息进行变量筛选,将筛选后的变量纳入最常规的Logistic回归模型进行建模预测,从而达到将重要的信息应用于最普遍、最易于理解和解释的传统统计学模型的效果。虽然机器学习和深度学习方法在医学领域应用的越来越广泛,但Logistic回归的优势仍然是不能被忽视的,如其所提供的OR值等指标,能够将变量对于结局影响的方向和程度进行很好地解释,这也是其在临床普遍应用的原因之一[16]。对于Logistic回归无法解决变量间存在的交互作用和共线性等问题,本研究使用深度学习和机器学习方法预先进行了变量筛选,并最终回归到Logistic回归模型,将机器学习和传统统计学模型的优势相结合,得到了优于仅使用一种方法建模所得出的结果。相较于其他同类研究,本研究模型的预测效果也具备一定优势。Ge等[34]的研究将RNN-LSTM模型和Logistic回归模型分别用于对4 896位ICU患者进行死亡风险预测,所得到的AUC分别为0.761和0.741。Xia等[13]的研究将LSTM集成算法用于对18 415位ICU患者进行院内死亡风险预测,模型的AUC为0.845。Gandin等[23]的研究将LSTM模型用于对10 616位来源于MIMIC-Ⅲ数据库的患有心血管疾病的患者进行7 d内死亡风险预测,AUC为0.790。考虑到本研究样本量较小,因此模型具备较好的预测性能。
本研究存在一定的局限性:首先,选取脑卒中患者作为研究对象在一定程度上限制了样本量的大小,深度学习算法的优势在于其可以有效地实现预测变量和结局变量之间的复杂映射,但需要大量的样本对模型的参数进行推断[35],因此,本研究的样本量对深度学习模型的预测效果产生了一定的影响;其次,本研究建立的预后预测模型是基于最大值、最小值、均值和标准差扩充后的数据建立的,虽然可以通过OR值获得变量与结局的关联强度,但是在解释上仍然存在一定的困难,如变量的标准差对结局的影响并不能较为直观地应用于临床;第三,本研究仅纳入了患者基本信息、实验室检查、生命体征和合并症相关变量,而对于包括机械通气在内的手术、包括输液在内的液体流入、包括尿量在内的液体输出和用药信息并未纳入,因此在一定程度上影响了模型的预测效果;最后,本研究建立的预测模型并没有进行外部验证,因此其具体价值还需进一步考量。
综上所述,基于引入注意力机制的LSTM和L1正则化的Logistic回归筛选变量,并通过传统的Logistic回归建立的预测模型效果较好,有利于辅助临床决策和预后评估。

