基于边缘计算的低压用户窃电检测

郑应俊，杨艺宁，舒一飞，薛阳，刘爱国，苏盛

（1.长沙理工大学电气与信息工程学院，湖南省长沙市 410004；2.中国电力科学研究院有限公司，北京市 100192；3.国网宁夏电力有限公司营销服务中心（计量中心），宁夏回族自治区银川市 750001）

0 引言

低压用户窃电是长期存在的痼疾，除直接导致供电企业利润流失外，窃电用户私拉乱接还是造成触电等人身伤亡事故的重要诱因［1-3］。因为数量庞大且用电行为模式多元，低压用户的窃电检测一直没有得到很好的突破［4］。

智能电表的普及应用为开展数据驱动的窃电检测奠定了坚实基础。文献［5］结合最大信息系数与密度峰值快速聚类算法来检测窃电。文献［6-7］基于每个用户前后多日负荷标准差的波动性指标、负荷序列升降的趋势性指标以及用户多日的负荷均值差值和变化斜率的变动性指标，采用改进后的离群因子算法来检测异常用户。针对特征提取影响异常检测准确率的问题，还可采用堆叠去相关自编码器提取高度凝练的独立特征，再利用支持向量机判断用户异常［8］。供电企业稽查人员有限，误报率是评价窃电检测算法实用性的核心指标［9］。工程应用中为避免误报，往往面向高损台区进行用电检查，以提高稽查靶向性。文献［10］利用多数窃电手段下异常用户窃电量与计量电量相关的特点，采用Granger因果分析检测造成线损异常波动的用户。此外，利用台区高损与用户计量异常具有关联性的特点，也可以通过其他信息的关联分析来实现低误报率的窃电检测［11］。

需要指出的是，台区低压用户通信异常多发，通信失败后常延迟几天后一次报送多日电量。根据主站数据统计台区线损电量时，用户数据报送失败当日会造成台区异常高损，而补报电量时又会造成台区低损甚至负损。现有窃电检测方法以数据完整准确为前提，采用失真数据进行窃电检测易导致错误结果，阻碍低压用户窃电检测工作的开展。

针对因台区数据缺失而无法进行准确窃电检测的问题，提出一种基于边缘计算的低压用户窃电检测方法。首先，比较分析了缺失数据的补全方法；然后，在通信正常和异常的条件下，分析台区窃电用户用电量与线损电量的关联关系，并利用台区智能终端（intelligent terminal of distribution substation，ITDS）可完整准确地就地采集用户数据的特点，提出基于边缘计算的低压用户窃电检测框架；最后，基于实际含窃电用户台区数据，验证了所提方法相比于在主站侧采用异常数据以及采用不同缺失数据填补算法修复后的数据进行窃电检测时的优势。

1 电力缺失数据补全方法

由于量测数据在测量与采集、传输与转换等各个环节均有可能受到干扰甚至发生故障，因此数据缺失错漏是电力系统长期存在的问题。传统上，对于电网冗余配置量测的状态量，可以在实现状态估计可观性的条件下采用伪量测的方式代替少数缺失数据。智能配用电系统中，用户用电数据同样存在数据缺失错漏的情况。此类数据难以用状态估计填补［12］，传统方法主要采用均值填补、最近距离填补、多重插补、回归模型和基于最大期望算法等补全模型［13］，这些处理方法多基于数理统计和机理分析构造数学模型，对用户侧缺失数据的重建效果并不理想，忽视了电力系统中量测的相关性和时序特性［14-15］，影响了基于重建数据进行决策分析的合理性。

由于缺失数据填补在很多科学和工程领域都有广泛的应用，近年来科研人员围绕该问题开展了大量研究并取得了较大进展［16-17］。在Netflix 推荐系统运用的矩阵填充方法建立在数据矩阵具有低秩性和稀疏性的前提下，可以在原始数据部分丢失的异常情况下，准确重构原始矩阵。低秩矩阵补全理论是基于数据本身的低秩性恢复缺失数据，它将矩阵秩最小化作为目标函数，经典的数据恢复数学模型为:

式中:‖ · ‖*表示矩阵核范数；K为恢复后的低秩矩阵；M为只观测到部分元素的待修复矩阵；Ω为M中非空元素位置集合，若矩阵M的元素Mi，j被观测到，则有(i，j)∈Ω；PΩ(·)为算子。由于实际系统一般存在高斯噪声和尖峰等形式噪声，考虑含噪声的实际数据的数据恢复模型如式（3）所示。

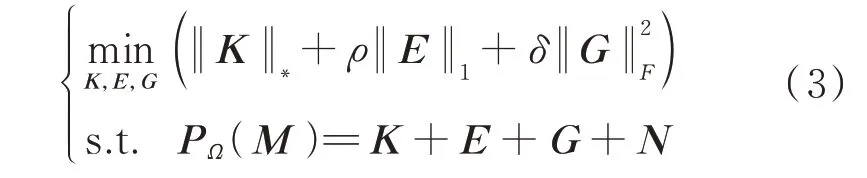
式中:E为尖峰异常值矩阵；G为高斯噪声矩阵；ρ和δ为相应的权重系数；‖ ·‖F表示F范数；N为辅助矩阵。求出式（3）中的增广拉格朗日函数并将其转化为无约束优化问题后，可根据文献［18］采用交替方向乘子法（alternating direction method of multipliers，ADMM）求解，不再赘述。

建立在矩阵填补基础上的张量填补，实际上是一种高维矩阵填补。由于多个用户在不同日的用电数据可能具有潜在的多维内在相关性，采用张量填补可利用更宽维度上的信息提高缺失数据填补效果，并已在低压台区缺失数据上得到成功应用［19］。张量填补的基本原理与矩阵填补类似，详见文献［19］。

与矩阵填补和张量填补利用数据本身的低秩性恢复缺失数据不同，生成对抗网络（generative adversarial network，GAN）方法采用数据驱动的方式，通过GAN 的对抗博弈对大量无标签数据进行特征提取训练，获得能够准确识别数据真假性的判别模型和捕获数据潜在特征与时空分布特性的生成模型。然后，采用双重语义感知约束重新训练模型，找到与含缺失值的待重构数据拥有最大相似性的备选数据，即可将其对应位置数据填补缺失部分数据［20］。需要指出的是，GAN 方法需要从大量数据样本中抽取数据的分布特性才能保证填补效果，对于单个台区用户缺失计量数据填补的适用性不强，本文采用矩阵填补和张量填补进行失真数据的填补。

2 基于边缘计算的低压台区用户窃电检测

2.1 低压台区用户电量与线损电量的关联性分析

配电台区非技术线损主要由窃电所致，非零电量窃电用户的窃电量与电表计量电量大多呈正相关，这会使得线损电量与窃电用户计量电量之间存在潜在的因果关联。因此，可用归因分析识别台区线损与接入用户计量电量的相关性，以识别嫌疑用户，提高窃电稽查的靶向性。

采用某实际高损台区数据分析用户电量与线损电量间的关联性。该高损台区62 天的实际线损电量如图1 所示，台区日均供电量约为1 200 kW·h，接入6 个工商业用户和33 个低压居民用户。2020 年1 月至2 月间，日均线损电量约为100 kW·h，线损率达到9.6%，不属于正常范围，可认定存在异常用电行为。因接入的工商业用户窃电影响和用电量显著高于居民用户，采集2019 年12 月30 日至2020 年2月29 日间日线损电量G及工商业用户1 至6 的日电量H1至H6进行分析。

图1 高损台区接入用户用电量及线损电量Fig.1 Electricity consumption of users and line loss power in high-loss distribution area

由图1 可见，整体上高损台区线损电量曲线与接入用户电量的趋势相似，均呈先升后降的形态。如果能找出用电量与线损电量因果关联性最高的用户，那么就可将其识别为窃电嫌疑最大的用户。

2.2 低压台区数据通信及异常分析

ITDS 一般安装于配电房二次侧［21］，在台区内采用RS485 或载波通信，系统主站采用无线专网或光纤通信，将采集的配变自身和台区低压用户计量数据向主站报送［22-23］。台区通信架构如图2 所示。

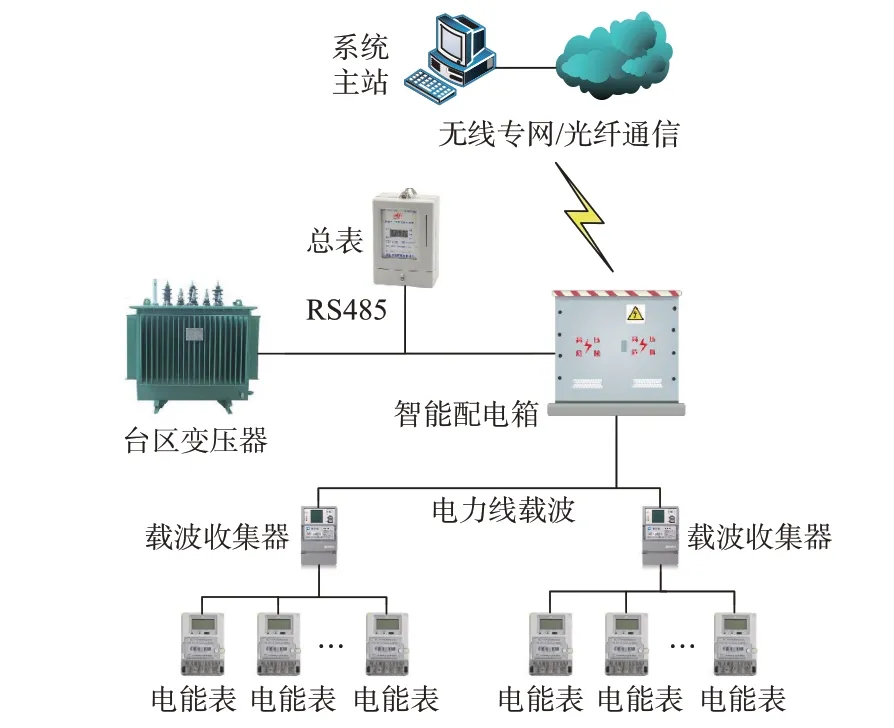
图2 配电台区通信架构Fig.2 Communication architecture of distribution area

实际系统中，用户通信失败延后1 至2 天上报数据的情况多发。为呈现通信异常对主站数据的影响，随机选取1.1 节高损台区的任一工商业用户（如用户1）在某一天（如2020 年1 月29 日）报送电量异常并在次日补报，实验结果如图3 所示。在通信异常日，线损电量和线损率会因为少报电量而突增，而在次日又会因为一次报送异常用户2 天的电量而骤降甚至出现负线损。通信异常使得主站侧线损电量发生畸变失真。采用主站侧失真数据进行窃电检测，可能打破窃电用户计量电量与线损电量之间的因果联系，使窃电检测产生错误的结果，难以准确识别窃电用户。

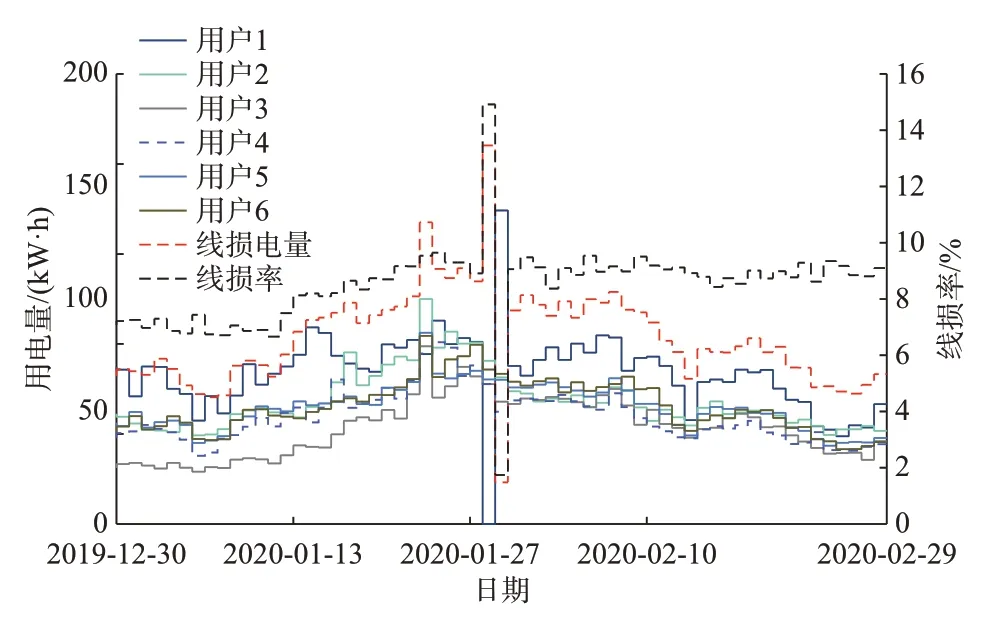
图3 通信异常时用户用电量及线损电量Fig.3 Electricity consumption and line loss power with communication anomaly

2.3 配电台区边缘计算与窃电检测框架

经济学中常用协整检验与Granger 检验来分析时间序列间的相关性。一般先采用协整检验检测序列间是否存在长期的均衡关系，然后采用Granger检验判断一个变量能否对另一变量产生影响［24-26］。考虑到多数窃电方式下异常用户窃电量与计量电量呈正相关，异常用户窃电引起的台区损耗波动与经济变量类的时间序列在受到其他因素干扰时的变化具有相似性。因此，可利用台区线损电量与用户电量两者间的均衡关系及因果联系，检测引起台区线损异常的用户。

传统上，受现场终端计算资源约束，只能将业务功能集中部署于中心主站等核心节点，系统性能取决于通信网络和主站的性能水平［27］。近年来，物联网终端的爆炸性增长和应用多元化带来了海量数据，在传输带宽和时效性上对中心化的数据处理方式提出了严峻挑战。计算机技术的发展使得边缘侧终端具备较强的计算处理能力，在靠近物联网终端以边缘计算的方式就近提供服务，可减少数据传输量，降低服务响应时延，增强网络效能［28-29］。

ITDS 是边缘计算技术在配用电系统应用的典范。它作为服务台区的综合平台，可以在边缘侧基于台区基础数据提供线损分析、电能质量监控、拓扑分析和户变关系分析等业务。因为不同业务功能模块可能由各厂家按存在差异的系统环境设计实现，需要采用容器技术支撑软、硬件解耦，从而在同一平台上实现不同厂家的业务系统功能［30］。基于容器技术的ITDS 包含系统层和应用程序（APP）层。APP 层分为采集APP 和业务APP，相互间可通过消息总线交互。采集APP 可采集台账数据、实时运行数据和负荷数据；业务APP 通过设备总线访问数据中心，提取所需数据进行计算分析，实现业务功能的边缘计算［31］。

结合2.1 节的低压窃电用户与台区线损关联分析与2.2 节的配用电物联网边缘计算架构，提出基于边缘计算的低压用户窃电检测方法。该方法的核心是利用ITDS 的集中器APP 就地获得台区用户计量数据，然后线损APP 根据台区供电量和用户电量分析线损电量，最后在窃电检测APP 中对台区线损和用户电量采用Granger 归因分析或其他算法来识别窃电用户，并将检测结果上传至云端，实现流程如图4 所示。本文所提方法将窃电检测从主站系统迁移至边缘侧进行，能够釜底抽薪地规避通信异常引起的数据失真问题，从而充分发挥窃电检测算法准确识别低压台区异常窃电用户的效能。

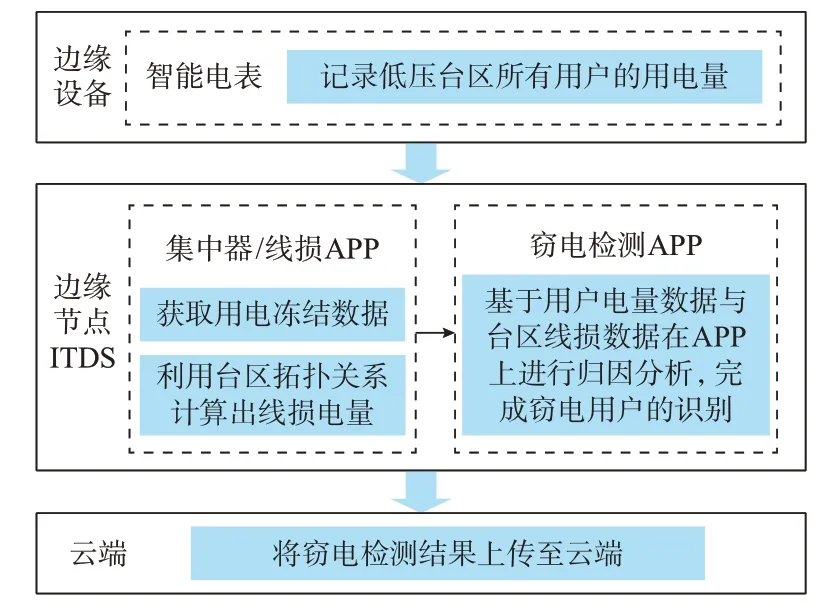
图4 基于边缘计算的窃电检测框架Fig.4 Electricity theft detection framework based on edge computing

3 异常检测算例

首先根据1.1 节中高损台区实际数据，采用Granger 归因分析方法进行窃电检测测试分析，然后将主站侧失真数据和失真后经矩阵填补和张量填补的数据进行对比测试。

3.1 边缘检测测试算例

在边缘侧对G、H1至H6及其差分序列分别完成单位根（ADF）检验。以5%的置信度为标准，序列均为一阶单整序列，检验结果见附录A 表A1。

分别对G、H1至H6采用Engle-Granger 协整检验，再通过ADF 检验对残差序列完成平稳检测，残差序列平稳性检测结果如表1 所示，表中红色数字表示检验值小于检验阈值-3.436 3。

表1 用户与线损电量的残差序列平稳性检验结果Table 1 Residual sequence smoothness test results of user and line loss power

残差序列平稳时对应变量间的回归方程为:

式中:T1和T2为相应参数的t检验值；R2为可决系数；为调整后的可决系数；Ftest为模型F检验值；D为杜宾沃森统计量。若F检验值和t检验值表现显著，则方程回归效果较好。

对H1至H6和G分别构建最小二乘回归模型，协整检验结果显示，H1至H3与G的残差序列平稳性检验中检验值大于检验阈值，而H4至H6与G的残差序列平稳性检验中检验值小于检验阈值，说明只有H4至H6与G存在协整关系，可继续完成后续的Granger 检验，检验阈值参考麦金农协整检验临界值［32］。为进一步明确H4至H6与G间的动态关系，需建立H4至H6与G间的误差修正模型:

式中:ΔH6为H6的一阶差分；et-1=G(t-1)-17.019 7 -1.322 5H6(t-1)，其中H6(t-1)为H6的滞后1 期序列。

当H4至H6在短期内波动（增加）1%时，H4至H6将在原基础上分别增加0.704 0%、1.230 2% 和1.101 9%。从误差修正项的系数来看，当H4至H6与G短期波动偏离二者间的长期均衡关系时，将分别 以-0.570 0、-0.445 7、-0.440 9 的调整力度将H4至H6与G间的非均衡状态修正至均衡状态。

分析H4至H6与G间的协整关系及误差修正模型发现，H4至H6与G的3 个误差修正模型中的误差修正项系数均符合反向调整机制。基于上述分析进一步厘清了存在协整关系的H4至H6与G之间长期稳定的特征以及在短期波动上的动态关系。在H4至H6与G之间均存在协整关系的基础上，进一步通过Granger 检验分析它们之间影响的因果联系，表2为边缘侧Granger 检验结果。由表2 可见，在5%的临界水平下，假设“H4不是G的Granger 原因”的显著性水平小于0.05，说明拒绝了原假设，所以H4是引起G变化的原因，可将H4视为台区中具有窃电嫌疑的用户。经现场稽查确证用户4 存在私接线路窃电。

表2 边缘侧Granger 检验结果Table 2 Granger test results at edge side

3.2 主站检测对比实验

低压用户通信失败后推迟上报数据，此时主站端数据将失真地表现为台区高损或负损，误导窃电检测结果。为验证本文所提方法的优势，挑选该台区的任一工商业用户在某一天如第31 天（2020 年1 月29 日）报送电量数据失败，并在次日补报。此时，线损电量和线损率在当天会因为少报电量而增大，而在次日又会因为一次报送异常用户2 天的电量而明显减少。用户H1至H6电量缺失后的用电量与线损电量结果见附录A 表A2。继续采用Granger因果检测法基于失真数据检验各用户与变化后的线损电量是否存在相关性。主站侧的Granger 检验总结果如表3 所示，用户H1至H6的电量缺失时的各部分检验结果见附录A 表A3 至表A5。由表3 和表A3 至表A5 可得出以下结论。

表3 主站侧Granger 检验结果Table 3 Granger test results in main station

1）用户报送数据失败时，异常用户用电量与台区线损电量间不存在协整关系，无法继续使用Granger 因果检验；其余用户用电量与线损电量仍存在协整关系，可继续使用Granger 因果检验。

2）除报送数据异常用户外，其余用户均可被认定为窃电嫌疑用户。因用户4 是稽查确认的窃电用户，低压用户报送电量失败再补报时，根据主站数据检测窃电用户的误报率上升到80%。

缺失数据填补是目前国内外研究的热点问题。文献［18］提出了一种基于低秩矩阵理论的电能质量缺失数据填补方法。该方法设计多范数联合的低秩优化模型，并采用ADMM 求解模型。文献［19］提出一种基于张量的多用户缺失电力数据的补全方法，在配电网低压台区缺失数据补全中采用了低秩张量补全模型。该方法通过对低压台区数据的特征进行分析，构建了该台区的标准缺失张量。然后在考虑用户数据自身特性和多用户数据多维内在相关性的基础上，利用补全张量的低秩性来建立模型，采用ADMM 迭代求解。

采用主站侧逐个用户数据传输失真时的算例数据，对通信异常未报送电量的用户数据按矩阵填充和张量补全2 种方式填补缺失的用户电量。出现数据传输异常用户在2020-01-29 和2020-01-30 的实际电量和2 种方式填补后的电量如表4 所示。2020-01-29 和2020-01-30 的实际线损电量分别为115.30 kW·h 和118.13 kW·h。根据填补校正的用户电量，可以计算校正后的线损电量及对应误差百分比，计算结果如表5 所示。

表4 填补电量缺失后的日用电量Table 4 Daily electricity consumption after recovery of missing power data

由表4 和表5 可见，尽管现有研究一般认为矩阵填补和张量填补能较好地填补缺失数据，但这种有效性是建立在数据具有低秩性的前提下的，当台区中用户数据相互间不具有较强的关联性时，也并不一定能准确恢复缺失数据。采用填补后的数据测试Granger 因果检测法能否准确识别窃电用户。2 种方法填补后的Granger 检验结果如表6 所示，矩阵填补后用户H1至H6的电量数据的各部分检验结果见附录A 表A6 至表A8。对比表4 至表6 和表A6 至表A8 可得以下结论。

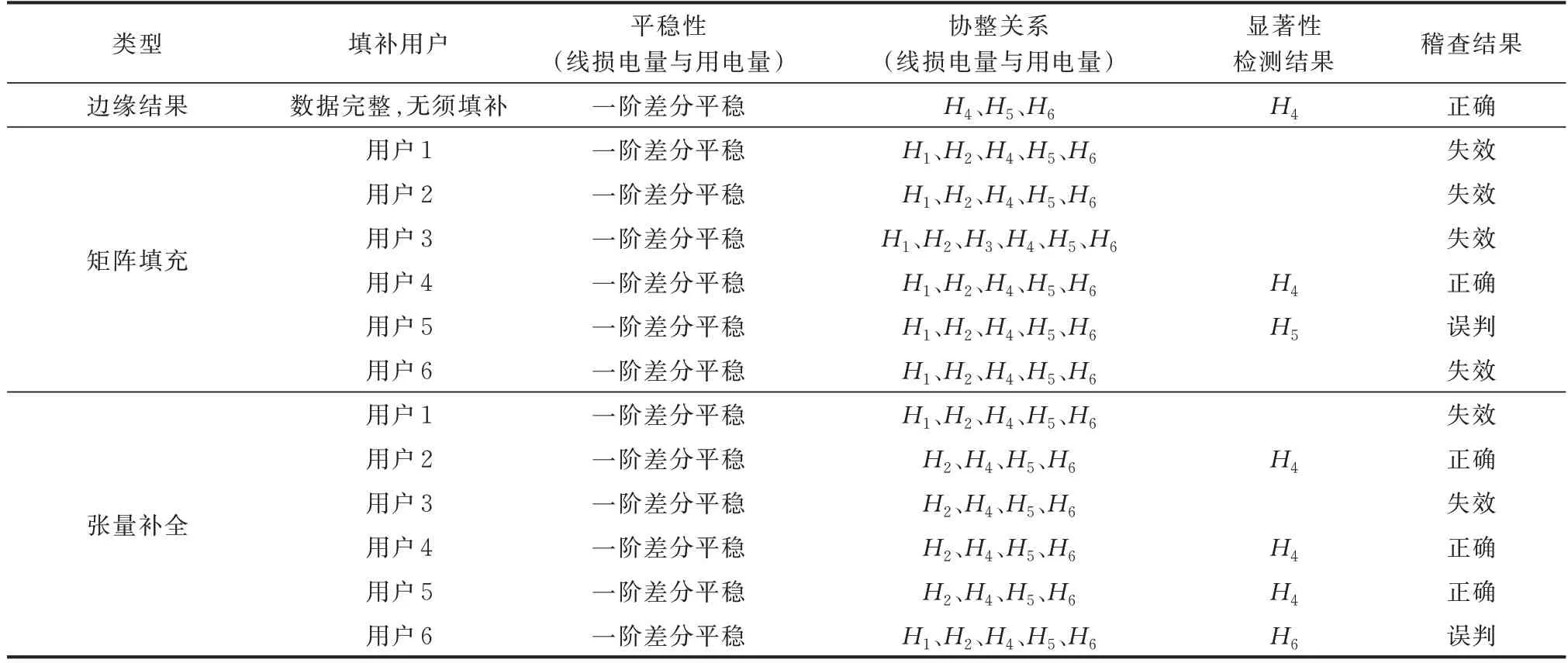
表6 主站数据填补后的Granger 检验结果Table 6 Results of Granger test after data recovery in main station

1）由矩阵填补后的数据分析可知，用户H1至H3、H6通信异常并填补恢复时，Granger 分析无法判断哪个用户的窃电嫌疑最大；用户H4通信异常并填补恢复后，会将用户H4判断为窃电嫌疑最大的用户，检测正确；用户H5通信异常并填补恢复后，会将用户H5误判为窃电嫌疑最大的用户，根据矩阵填补的主站数据检测窃电用户的正确率显著下降到16.6%。

2）由张量补全后的数据分析可知，用户H1、H3通信异常并填补恢复后，Granger 分析方法无法判断哪个用户的窃电嫌疑最大；用户H2、H4、H5通信异常并填补恢复后，会将用户H4判断为窃电嫌疑最大的用户，检测正确；用户H6通信异常并填补恢复后，会将用户H6误判为窃电嫌疑最大的用户，根据张量补全的主站数据来检测窃电用户的正确率下降至50%。

3）矩阵填补和张量填补的目标是得到范数最小的低秩矩阵/张量，为得到低秩的补全数据，使得补全后的数据在一定误差范围内具有更高的线性相关性，在一定程度上改变用户与线损电量的相关性。从表4 和表5 可知，2 种补偿算法均有误差。由文献［10］中Granger 检验关系式可知，同一时间点被检测用户用电量和线损电量的一一对应关系对最终检验结果影响很大，而补全算法在一定误差范围内改变了此种相关关系，从而导致Granger 检验无法准确识别窃电用户。

表5 填补电量缺失后的损失电量Table 5 Loss power after recovery of missing power data

综上，采用相同方法进行窃电检测，不管是矩阵填充还是张量填充恢复失真数据，都会造成准确率明显下降。本文所提方法只需要将计算模式切换到边缘侧执行，即可消除数据失真引起误报的问题，显著降低误报率，提高低压用户窃电检测的准确性。

3.3 工程验证

某供电企业营销服务中心采用本文所提出的基于边缘计算的低压用户窃电检测方法进行验证。该地区线损率在5%以上的高损台区共计2 130 个，其中配置有智能融合终端、可执行边缘计算的台区为124 个，配置的智能融合终端如图5 所示。

图5 典型台区的智能融合终端Fig.5 Intelligent fusion terminal in typical distribution area

采用本文所提方法进行边缘侧窃电检测。从配变融合终端上抽取50 个实际高损台区在边缘侧汇聚的2021 年8 月至11 月间台区和用户计量数据进行窃电检测。

由于Granger 归因分析有数据序列同阶的要求，有18 个台区无法检测。在满足同阶要求的32 个台区中，检出38 个疑似窃电用户，其中7 个台区未检出异常用户。对38 个用户下发窃电检测工单，经现场查实窃电用户有29 户，准确率为76%。其中，存在一个窃电用户的台区有11 个，存在2 个窃电用户的台区有9 个，不存在3 个及以上窃电用户的台区。

对于查实有异常用户的20 个台区，根据主站侧计量数据采用效果较好的张量补全缺失数据后，再用Granger 归因分析进行窃电检测。其中，6 个台区能准确检出查实的窃电用户而无误判，共检出7 个窃电用户；4 个台区既检出窃电用户，又存在误判用户，共检出4 个窃电用户；5 个台区检出的用户均为误判用户；5 个台区既没有检出也没有误判窃电用户。准确检出率为37.9%，明显低于采用边缘侧准确数据的识别准确率。

4 结语

针对用电信息采集系统主站低压计量数据失真影响窃电检测的问题，提出了基于边缘计算的低压用户窃电检测方法，主要结论如下。

1）分析指出低压用户通信异常导致主站计量数据失真，采用失真的计量数据进行高损台区窃电检测易造成误报，是阻碍低压用户窃电检测的重要因素。

2）针对难以根据失真的低压台区数据准确检测高损台区窃电用户的问题，提出以边缘计算方式在ITDS 上进行窃电检测的新模式，因为采用本地数据，可以釜底抽薪地消除低压用户通信异常导致主站数据失真对窃电检测的干扰和影响。

3）基于高损台区实际数据，产生了通信异常数据、矩阵填补和张量填补失真数据。

4）基于以上4 种模式下的数据应用Granger 归因分析进行用电异常检测。测试结果表明，主站数据失真可导致线损归因分析方法将所有用户均判别为异常，导致窃电检测完全失效。采用矩阵填充失真数据时，检测准确率降低到16%；采用张量补全失真数据时，检测准确率降低到50%；而采用本文所提边缘计算方式进行窃电检测，不受通信异常影响，可准确检出窃电用户。

本文仅以Granger 归因分析方法为例，验证所提方法的有效性，其他时间序列分析方法也可用于识别对线损异常有贡献的异常用户，但数据失真对检测效果的影响也是相似的。此外，因为零电量低压用户可用信息不足，本文所提方法不能用于检测零电量窃电用户。如何突破信息缺失的影响，是后续窃电检测的重点研究方向。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。