基于时空图卷积网络的电力系统暂态稳定评估
庄颖睿,肖谭南,程 林,陈 颖,关慧哲
(清华大学电机工程与应用电子技术系,北京市 100084)
0 引言
在“碳达峰、碳中和”的目标下,电网结构逐步呈现出复杂多变的新形态特征,电力系统面临更多暂态稳定风险。快速、准确的电力系统暂态稳定评估对电力系统的安全稳定运行至关重要。近年来,深度学习的巨大发展推动了模式识别与数据挖掘相关的研究[1],在暂态稳定评估中也得到了应用。
一方面,电力系统受扰后状态变量与运行变量的变化曲线能够直接反映电力系统暂态稳定性。文献[2]将故障后短时间内各节点的电气量测数据设计为二维矩阵,应用卷积神经网络(convolutional neural network,CNN)卷积提取特征以实现稳定评估。文献[3]基于一维卷积神经网络(1D-CNN)提取电气量测数据中的时序特征来准确刻画暂态稳定状态。文献[4]基于长短期记忆(long short-term memory,LSTM)网络读取故障切除后系统电压波形来判断稳定性。文献[5]依据电力系统暂态过程中部分电气量测数据的时序特性,建立双向长短期记 忆(bi-directional long short-term memory,BiLSTM)网络进行稳定预测。
另一方面,电网拓扑直接影响电力系统的整体能量分布与能量变化路径。文献[6]针对电网的图拓扑邻接关系和节点信息的相关性,引入图注意力网络(graph attention network,GAT)建立暂态稳定评估模型。文献[7]基于消息传递图神经网络(message passing neural network,MPNN),通过提取图拓扑的空间变化特征来判断暂态稳定性。文献[8]将图卷积网络(graph convolution network,GCN)应用于电力系统暂态评估,使用GCN 来挖掘拓扑变化中的空间特征。文献[9]将GCN 和LSTM 相结合提出递归图卷积网络(recurrent graph convolutional network,RGCN),使用GCN 来捕捉空间特征,使用LSTM 网络来捕捉时间特征。
总体来看,现有用于电力系统暂态稳定分析的深度学习模型,对暂态过程中时间特征与空间特征的耦合关系关注不足。由于故障发生、保护动作、安全稳定控制等,大扰动下电力系统的暂态过程呈现出明显的时空关联特性。对于深度学习模型,与目标相关的先验知识的引入往往能够明显提高模型的预测精度。从理论上看,同时关注电力系统暂态过程中空间特征与时间特征的深度学习模型,既能够利用更多与稳定性相关的信息提高暂态稳定预测的准确性,又能够利用空间特征对不同时间特征之间的相互影响形成一定的约束,提高模型的可解释性。但是相应的,模型也变得更加复杂,训练耗时增加,影响预测速度。因此,尽管拓扑信息的引入能够提高模型性能,现有大多数同类研究出于各自应用场景与所需模型性能的综合考量,并未对暂态过程的时空特征作综合考虑。
实际电力系统中,离线运行方式计算、在线预决策紧急控制[10]、实时决策紧急控制[11]都需要完成大量的暂态稳定仿真。海量仿真运算耗时极大,但也为模型的训练提供了所需样本,且仿真过程中电网拓扑信息的获得相对简单。因此,本文针对电力系统暂态稳定仿真分析场景,提出了一种能够同时挖掘暂态过程中的空间特征和时间特征的时空图卷积网络(spatio-temporal graph convolutional network,STGCN)模型,探索基于时空特征挖掘的深度学习模型在电力系统暂态稳定性预测方面的性能表现。该方法使用门控卷积(Gated CNN)[12]与GCN 提取系统时空特征,使用图的二阶池化方法[13]增强图池化分类性能,实现从短时仿真数据端到稳定类别判断端的样本映射,并在新英格兰10 机39 节点系统中进行验证。
1 STGCN 模型
1.1 基于图卷积的空间特征提取
由于传统的CNN 无法处理非欧氏空间的数据,研究人员定义了能够处理图域数据的神经网络结构:图神经网络(graph neural network,GNN)。2005 年文献[14]提出图神经网络的概念,2013 年文献[15]将卷积引入图神经网络,并基于频域卷积的概念提出了一种图卷积网络模型,将可学习的卷积操作应用到图域数据上。本文采用的GCN 实现方式为使用图傅里叶变换在谱域上对图进行操作,引入频谱框架在频域中应用卷积,通常称为频域图卷积[15]。
将电力系统网络拓扑抽象为图结构,并在频域上可以使用归一化的拉普拉斯矩阵来表示电力系统拓扑图的结构特征:
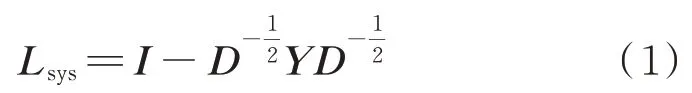
式中:将导纳矩阵Y作为电力系统拓扑图的带权重的邻接矩阵A,权重为线路导纳;I为单位矩阵;D为图的加权出线度矩阵,其元素,其中Aij为A的元素。
对拉普拉斯矩阵进行谱分解以进一步提取特征:
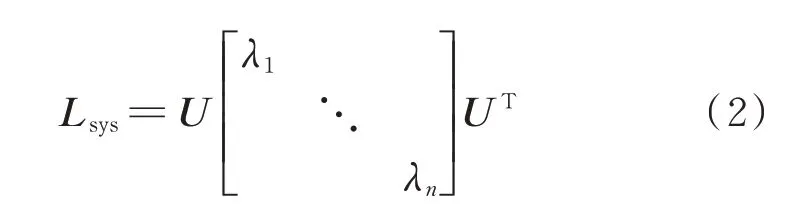
式中:U=[u1,u2,…,un]为列向量是单位特征向量的正交矩阵,满足UUT=I;n为特征值总数;λi为矩阵特征值,其中i=1,2,…,n。
类比传统的傅里叶变换,可以得到图的傅里叶变换的矩阵形式:

式中:Xg为图的特征向量;为图的傅里叶变换矩阵。
类比传统的函数卷积,可以得到图卷积公式:

式中:⊙表示哈达玛积;*表示图卷积;g为卷积核;(Xg*g)G表示在图G上应用图卷积。
定义gθ=UTg为可学习的卷积核,得到图卷积公式:

式(5)计算量较大导致计算速度较慢,为降低计算复杂度,可使用切比雪夫多项式来拟合卷积核[16]:
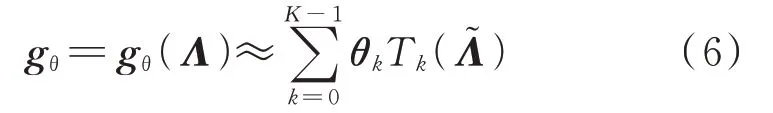
式中:Λ为Lsys矩阵的特征值构成的对角矩阵;=2Λ/λmax-I为缩放之后的特征向量矩阵,其中λmax为Lsys的最大特征值;Tk(·)为k阶的切比雪夫多项式;θk为对应的切比雪夫系数;K为切比雪夫多项式的项数。
切比雪夫多项式的递归定义为:

式中:T0(x)=1;T1(x)=x。
由此可得图卷积公式:
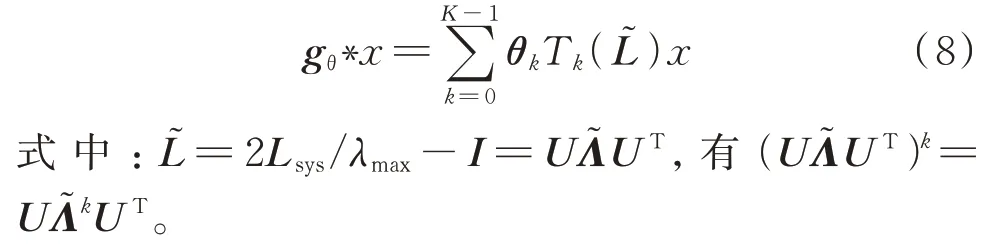
1.2 基于门控卷积的时间特征提取
在时间序列处理问题中,基于循环神经网络(recurrent neural network,RNN)的模型得到了广泛的应用。但是RNN 及其衍生模型LSTM 网络、BiLSTM 网络等仍然存在串行迭代耗时、门机制复杂等问题。受文献[12]的启发,本文在时间轴上使用Gated CNN 以更加快速地捕捉电力系统暂态过程中的时间动态特征,并使用残差连接[17]以减轻过拟合现象。
时间卷积层设计为由一个一维的因果卷积和随后作为非线性层的门控线性单元(gated linear unit,GLU)构成,能够对不同长度的时间序列数据进行特征提取。在时间卷积层中,每个节点的输入为一个包含Ci个输入通道、长度为M的序列,可表示为。设计卷积核,将输入的X映射为。所以,时间卷积层可以定义为:

式中:P、Q为GLU 中门的输入;Kt为时间卷积核的大小;Co为输出通道数;σ(·)表示激活函数,这里采用sigmoid 激活函数。
1.3 基于时空图卷积层的时空特征提取
为了同时提取电力系统暂态过程中的空间特征和时间特征,结合空间图卷积层和时间门控卷积层来构造时空图卷积层(spatio-temporal graph convolutional block,ST-Conv)。时空图卷积层的结构设计为在两个时间层中夹有一个空间层,从而实现两个时间卷积之间的快速空间状态传播[18]。时空图卷积层结构如图1 所示。
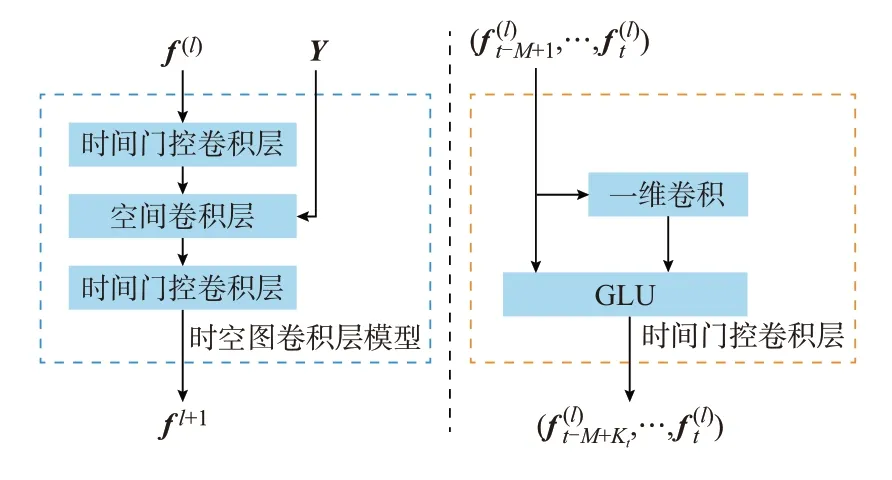
图1 时空图卷积层示意图Fig.1 Schematic diagram of spatio-temporal graph convolutional block
时空图卷积层中时间层的输入为潮流f,空间层输入为导纳矩阵Y。输入的潮流数据首先经过一层时间卷积层提取时间特征,结合Y经过空间卷积层提取空间特征并激活之后再次经过时间卷积层,最终得到综合时空特征的提取结果。基于图卷积式(8)与时间卷积层式(9),可以得到对于输入到时空图卷积块l的潮流(其中C(l)时空图卷积块l的通道数),输出的潮流计算为:
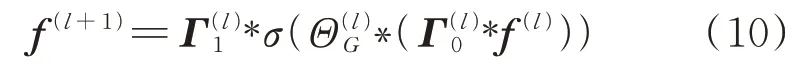
2 基于STGCN 的暂态稳定评估模型
构建STGCN 模型之后,需要结合实际问题对STGCN 模型的结构做进一步设计。
2.1 特征选择
电力系统暂态过程在空间结构上存在图域拓扑特性,在时间轴上存在动态特性。空间特征方面,电力系统网络的导纳矩阵Y中包含有图域结构特征,但由于电力系统网络的空间结构为非欧氏空间图域结构,无法使用传统的CNN 进行建模,所以需要针对图域结构使用GCN 来提取电力系统网络导纳矩阵中的空间特征信息。时间特征方面,系统潮流(PG,QG,PL,QL,U,θ)中包含时间动态 特性,其中PG、QG分别为节点发电机的有功功率和无功功率,PL、QL分别为节点负荷的有功功率和无功功率,U为节点电压幅值,θ为节点电压相角。构造t时刻时间特征ft=[PG,QG,PL,QL,U,θ]t,可在时间轴上应用卷积结构来提取时间特征。建立STGCN 以同时提取电力系统暂态过程的空间特征和时间特征,从而对暂态稳定进行预测。
按照故障发生与故障切除的2 个时间点可以将暂态过程分为故障前、故障中、故障后3 个时间段,分别对应3 个导纳矩阵Y0、Y1、Y2和3 段潮流曲线f0、f1至至fT,其中T为时间序列的长度。设计3 个暂态稳定分析模块分别对3 段特征进行分析,做出暂态稳定预测,并将3 个预测结果输入全连接层中综合,得到最终预测结果。其中,由于故障前的潮流时间特征长度只有一帧,不构成时间序列,故对故障前的特征只做空间上的图卷积,以一帧潮流时间特征作为图的特征向量。故障中与故障后的特征则构造时空图卷积模块进行特征提取,时间序列的长度根据所针对的电力系统的实际情况决定。综上,拓扑信息描述了电力系统能量传递路径特征,潮流信息描述了电力系统内部能量分布特征,拓扑与潮流信息的变化共同描述了电力系统外部激励特征。因此,对于一个元件参数确定的电力系统,不考虑安全稳定控制,3 个导纳矩阵Y0、Y1、Y2和3 段潮流曲线f0、f1至至fT将唯一地确定一个动态过程,电网稳定性是唯一的,保证了所选特征到电力系统稳定性间的映射是一对一的单映射。
2.2 模型结构设计
STGCN 整体模型结构如图2 所示,构建了1 个GCN 模块和2 个STGCN 模块来对3 段特征进行提取,将输出结果综合至全连接层(fully connectedlayer,FC),输出模型稳态预测结果。其中,为增强模型特征提取能力,同时尽量减轻过拟合现象,时空图卷积模块设计为由2 个时空图卷积层串联构成。

图2 STGCN 模型结构Fig.2 Architecture of STGCN model
其中,输出端的全连接层使用图的双线性映射二阶池化方法[13]来进一步提取特征表示,并对输出结果进行降维。与直接将特征维度压缩为一维的常规池化方法相比,二阶池化方法能够通过利用所有节点信息并提取二阶信息,在减少模型参数量的同时增强图池化的性能,得到更好的图分类效果。此外,二阶池化方法具备图节点的置换不变性,即对于相同网络但是节点编号不同的情况,二阶池化模块能够得到一致的特征表达。双线性映射二阶池化计算方法如式(11)所示:

式中:flatten(·)为一维化函数;Xh为经过全连接层得到的图的特征表示矩阵;W为二阶池化方法中的线性映射矩阵。Xh矩阵经过二阶池化之后,最终经过flatten 函数一维化处理得到最终模型的暂态稳定预测结果hG。双线性映射二阶池化示意图如图3 所示,其中fs表示特征数目,n表示节点数(与前文的特征值总数对应),w′与w表示变换之后的矩阵行数和列数。

图3 双线性映射二阶池化示意图Fig.3 Schematic diagram of second-order pooling of bilinear mapping
构建STGCN 模型,将3 个时间段内的导纳矩阵和潮流输入模型并进行训练,提取暂态过程中的时空特征,同时模型中引入了dropout 机制、残差连接、层标准化等方法来缓解过拟合问题,并且选取验证集损失最小时的模型作为最优模型。
2.3 模型输出
暂态稳定判断问题是一个二分类问题。模型输出设计为大小为1×2 的二值向量,[1,0]表示失稳,[0,1]表示稳定。稳定的判据参照暂态稳定指数ITSI[3-5]:
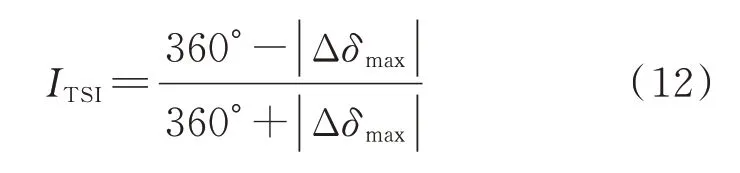
式中:Δδmax为任意2 台发电机之间的最大功角之差。当ITSI<0 时,系统不稳定;当ITSI>0 时,系 统稳定。
2.4 损失函数
对于二分类问题,一般使用二元交叉熵损失函数(binary cross entropy loss,BCELoss),计算式如式(13)所示:

式中:为预测输出;y为目标实际值。
3 算例测试
为了验证所提出的STGCN 暂态稳定分析模型的有效性,本文使用新英格兰10 机39 节点系统进行算例测试,该系统含有10 台发电机、39 条母线和46 条线路,代表着美国新英格兰地区的一个345 kV的电力网络,系统拓扑图如附录A 图A1 所示。
3.1 数据集描述
数据集来自对新英格兰10 机39 节点系统的故障仿真模拟,所使用的仿真软件为PSOPS[19-20]电力系统暂态仿真工具,该仿真工具可提供仿真过程中各个时刻的包括节点导纳矩阵、阻抗矩阵等拓扑参数在内的电网变量信息,其接口程序已在GitHub 开源。初始潮流采用完全随机采样方式获取,拓扑结构包括原始拓扑与任意N-1 拓扑,任一负荷均可在标准算例负荷的50%~150%范围内波动,任一发电机出力可以在零功率至额定功率之间波动,所得潮流样本均收敛并满足静态安全约束。故障类型包括节点故障、支路故障,故障切除时间设置为0.10 s。
如前所述,STGCN 模型选取的时间序列长度由所针对的电力系统的实际情况决定。综合考虑算例仿真结果数据特点与计算效率,本文使用仿真软件获取故障前、故障中、故障后的3 个导纳矩阵和故障前1 帧(即稳态潮流)、故障中10 帧、故障后20 帧共计31 帧从0~0.30 s 的系统潮流(PG,QG,PL,QL,U,θ)变化来构成数据集,共计获取58 240 个有效样本用于构造训练集、验证集与测试集,各样本集包含的样本数以及其中稳定样本与失稳样本的分布情况如表1 所示。
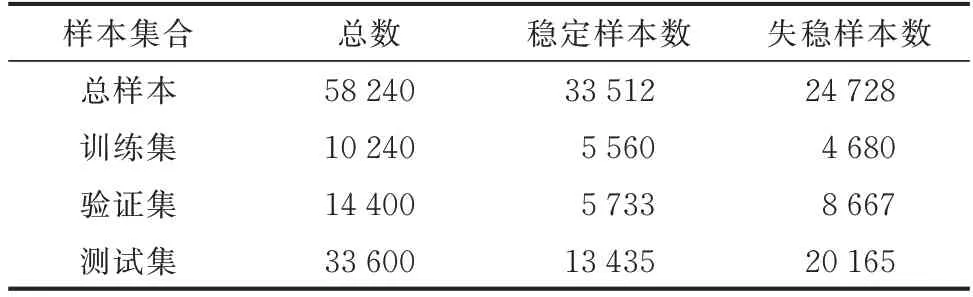
表1 样本集合的分类Table 1 Classification of sample set
3.2 模型训练参数设置
STGCN 模型的训练采用RMSprop 优化器,初始学习率设置为0.001,随机丢弃概率设置为0.1,每批训练数据数目设置为32,训练次数设置为30。其中学习率按照每训练5 次以0.7 的速率衰减。为评估模型表现,使用BCELoss 来计算模型损失,并且使用准确率(accuracy)、精准率(precision)、召回率(recall)、f1 分数(f1-score)作为评价算法性能的主要指标。
由于模型输出结果为一维概率值,本文设置预测分数阈值为0.1,如果预测值大于等于0.9,则认为系统失稳;若预测值小于等于0.1,则认为系统稳定;若预测值介于0.1~0.9 之间,则认为系统稳定性不确定。仿真分析场景下,预测结果为不确定的样本则选择进行完整仿真的方式判断稳定性。
3.3 模型测试结果
在模型训练过程中记录模型在训练集、验证集、测试集上的损失,绘制损失曲线如附录A 图A2 所示,可见模型达到较高的准确率。同时,使用t分布随机近邻嵌入(t-SNE)算法对数据特征进行降维可视化展示,结果及分析如附录A 图A3 所示,可以看到,经过特征提取后,稳定样本与失稳样本得到较好的分离。
计算混淆矩阵如表2 所示。

表2 STGCN 模型结果混淆矩阵Table 2 Confusion matrix for STGCN model results
由混淆矩阵结果可见,STGCN 模型对稳定与失稳样本进行了准确的判断区分,预测准确率较高,但存在12 例的“漏判”。由于电力系统存在高度的非线性,暂态稳定分析需要学习的信息较为复杂,目前“漏判”难以完全避免。一方面,STGCN 模型强大的时空特征提取能力让暂态稳定评估的准确率达到了非常高的水平;另一方面,进一步减小分类阈值能够减少“漏判”的发生[21],但也会增加不确定样本的数量。经测试验证,分类阈值设置为0.003 时,“漏判”数减少至0,“不确定”样本数增加为1 726。
计算用时上,STGCN 模型平均每条数据判稳计算用时仅需约0.005 s,所需的仿真时间从原本10 s 缩短到现在的0.3 s,满足仿真分析场景的需要。
为进一步考察本文所提出的STGCN 模型的性能,将基于二阶池化的STGCN 模型与基于常规池化且只考虑了时间特征的CNN、LSTM、多层感知机模型(multi-layer perceptron,MLP)、Gated CNN进行对比,构造多个训练集训练模型并测试,得到5 种模型各指标平均结果如表3 所示,绘制出图4 所示的比较结果图。
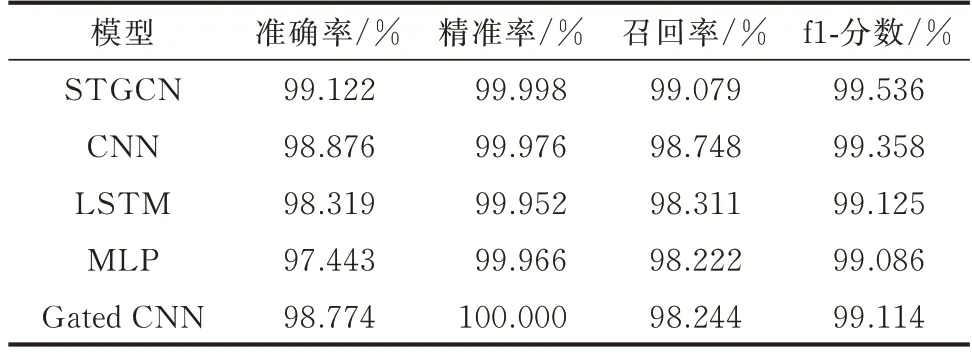
表3 5 种模型各指标平均结果Table 3 Average results of indicators of five models
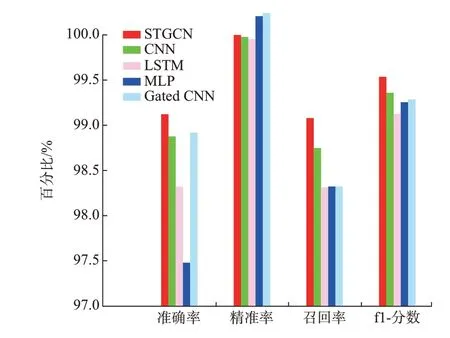
图4 5 种模型各指标对比图Fig.4 Comparison of indicators of five models
由表4 和图5 可见,STGCN 模型在准确率、精准率、召回率、f1 分数指标上均比CNN、LSTM、MLP、Gated CNN 模型更具有优势。
为了分析样本数量对模型性能的影响,训练集样本数分别设置 为2 560 条、5 120 条、7 680 条和10 240 条,测试集样本数为33 600 条。训练STGCN、CNN、LSTM、MLP、Gated CNN 这5 种模型,得到测试集上的准确率评估结果如图5 所示。
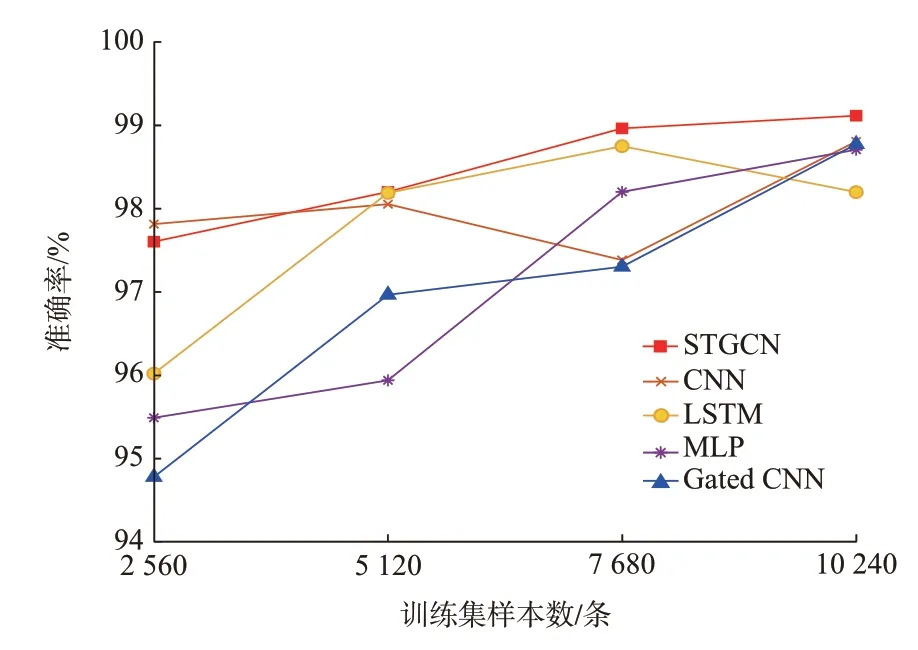
图5 不同训练集样本数下5 种模型的准确率结果Fig.5 Accuracy results of five models with different numbers of training set samples
由图5 可见,除在训练集2 560 条样本数时STGCN 模型的准确率略低于CNN 模型外,其他训练集样本数下STGCN 模型的准确率均高于其他模型。而在相同的测试准确率下,STCGN 模型所需要的样本数也是5 种模型中最少的。
另外,STGCN 模型的泛化能力也优于其他模型。模型泛化能力是指模型训练后对新样本的适应能力,一个泛化能力更优的模型能够在遇到新样本时展现出更好的性能。由STGCN 模型训练损失曲线来看,STGCN 模型损失小,准确率较高,且t-SNE算法降维可视化结果表明STGCN 模型实现了测试集样本的准确预测。另外,与CNN、LSTM、MLP、Gated CNN 模型相比,STGCN 模型在准确率、精准率、召回率、f1 分数指标上均更优,且能在训练集样本数量更少的情况下得到更准确的预测结果,表明STGCN 模型具有更强的泛化能力,能够更加充分发掘暂态过程中的特征变化。
3.4 模型结构优势分析
STGCN 模型的结构优势分析主要包括以下3 个方面。
1)STGCN 模块设计为2 个时空图卷积层串行的优势
本文所设计的STGCN 模块采用2 个时空图卷积层串行,可以加强时空特征提取以提高模型准确率。经测试,只使用一个时空图卷积层模块时,模型准确率为98.512%,低于2 个时空图卷积层串行时STGCN 模型的准确率99.116%。但如进一步加深层数,如采用3 个或3 个以上的时空图卷积层模块串行,则可能会由于模型过于复杂、参数过多导致出现反向传播梯度消失和过拟合现象。
2)全连接层采用二阶池化方法的优势
为考察二阶池化方法的分类能力,分别设置阈值为0.1、0.3、0.5,比较二阶池化方法与常规池化方法的准确率如表4 所示。其中,阈值设置为0.1 时,常规池化方法得到的预测结果均为“不确定”,故准确率等指标均为0。由以上结果可见,与常规池化方法相比,二阶池化方法能够增强图池化的性能,具有更强的特征提取能力。

表4 不同阈值下二阶池化与常规池化结果Table 4 Results of second-order pooling and regular pooling with different thresholds
3)时间特征提取采用Gated CNN 的优势
为验证Gated CNN 在时间特征提取上的性能,将时空图卷积层中的时间层设计为LSTM 模型,训练模型并测试。将时间层采用Gated CNN 模型的STGCN 模型简记为模型1,将时间层采用LSTM模型的STGCN 模型简记为模型2。训练时间上,模型2 约需1 120 min,而模型1 约需90 min;模型准确率上,模型2 准确率为90.934%,而模型1 准确率为99.116%。可见,与模型2 相比,模型1 能够在大量减少训练时间的基础上,提高模型准确率。模型2比模型1 参数量大得多,过于复杂的模型不仅训练困难,也容易出现过拟合的情况,造成模型2 准确率低于模型1。
综上所述,STGCN 模型与其他模型相比,性能上更具优势。这是因为与其他模型相比,STGCN模型进一步考虑并使用GCN 提取了电力网络中的能量传递通路空间特征变化,引入时间卷积-空间卷积-时间卷积的“三明治”式结构,通过中间的GCN网络实现在2 次时间卷积中间完成一次空间特征的快速传播,实现了空间上的特征变化与时间上的特征变化的综合提取,能够更好地挖掘暂态过程中的数据特征,具有更强的暂态评估能力。
4 结语
电力系统的暂态稳定分析是电力系统研究中的一个重要内容。本文的主要贡献在于:
1)以减少暂态稳定分析仿真所需时间为出发点,针对现有的基于深度学习的暂态稳定分析方法特征挖掘不足的问题,提出了基于STGCN 模型的暂态稳定预测方法,在模型中引入了GCN 作为空间层,Gated CNN 作为时间层,二阶池化方法作为全连接层。
2)比较了提出的STGCN 模型与CNN、LSTM、MLP、Gated CNN 模型在多指标上的性能差异,得到STGCN 模型具有更优性能的结论。并对STGCN 模型“三明治”式结构、时间层采用Gated CNN、全连接层采用二阶池化方法的设计进行了验证,验证结果充分体现出了所提方法的优越性。
目前,本文提出的STGCN 模型主要针对以仿真分析为基础的离线、在线分析场景,方法准确率高,能够有效缩短仿真时间,提高分析效率。在未来研究中,将针对部分在线分析场景下网络拓扑维护困难、高分辨率量测信息有限的问题开展研究,并对本文的STGCN 模型做进一步的模型适应性设计和改造,提高STGCN 模型在多种在线分析场景中的适应性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

