面向风电场发电曲线偏差校正的电化学储能系统容量规划方法
曹明浩,于继来
(哈尔滨工业大学电气工程及自动化学院,黑龙江省哈尔滨市 150001)
0 引言
由“十四五”规划可知,中国非化石能源占比将于2050 年提升至50%以上[1],风光发电项目平价入网政策导向得以明确[2]。随着火电逐渐退出,系统灵活性资源逐渐枯竭[3],间歇式电源随机波动性影响电网安全[4-5]。因此,提高风光场站功率预测精度和发电曲线偏差考核标准,加大计划外超标偏差功率(下文简称超标功率)处罚力度是必然趋势。除改善预测外,配置一定储能[6-8]实时校正超标功率是减少对系统灵活性资源过度依赖的重要举措[9]。
目前,主要立足两类应用来研究风光场站自配储能问题。一类应用是服务较长周期(如日、星期甚至季节)的削峰填谷[10-12]。然而,胜任于此的一般只有抽水蓄能电站。若采用电化学储能系统(electrochemical energy storage system,EESS),则因单位投资昂贵,其容量和调控周期均受到严重制约。另一类应用是服务较短周期(如几小时或数十分钟)的发电控制[13-16]。因短时预测精度受随机波动性的影响较小,故超标功率校正量较小、时间较短、次数较少,从而可将EESS 配置量控制在较小规模。此时,EESS 将具有比服务应用一时更高的潜能。本文侧重第二类应用,探讨面向风电场(WPF)发电曲线偏差校正的小规模EESS 容量规划问题。
文献[17]根据不同时间尺度风电功率的随机性与波动性优化储能容量配置方案;文献[18]考虑风电不确定性和弃风条件,应用鲁棒优化确定储能容量;文献[19]考虑储能使用寿命、运行成本和投资收益等参数,建立系统收益最大化模型;文献[20]分析了集中式或分散式WPF 采用不同波动平抑策略时的储能最优配置问题;文献[21]考虑充放电量与环境因素综合决策储能容量配置方案;文献[22]考虑风电并网所需辅助服务费用和储能成本,评估储能成本回收周期和经济效益;文献[23-25]研究了WPF 参与电力市场交易时的储能容量规划方法和使用策略;文献[26]针对能量型和功率型储能,兼顾风电波动与预测误差,优化储能总容量和两类储能容量配比方案;文献[27]考虑荷电状态(state of charge,SOC)、充放电速率、剩余容量约束与自放电率等因素,提出了使用储能校正超短期预测误差的方法;文献[28]提出风电功率预测和SOC 控制模型,减少电池进入能力死区时间,以提高偏差控制性能。
由于实际电网目前对WPF 发电曲线偏差普遍缺乏严格的考核,即使有考核,也仅局限于极少数限风时段,故已有研究在优化EESS 容量配置方案时,主要从时间尺度、分布类型、场景特征等方面重点考虑风电功率平滑性要求(中国各大电网公司重点考核10 min 和1 min 功率变化速率)。当WPF 发电计划曲线逐渐被严格化考核且需要应用EESS 校正超标功率后,除须研究实际场景中超标功率数值的概率分布(空间分布)特性外,还应考虑正负超标功率事件(下文简称超标事件)在短时窗内呈现的不均匀或不对称分布(时间分布)特性,即需要分析与考核时段(如15 min)相配套的、由单个或数个连续时段组成的短时窗内的累积净偏差电量自归零特性。合理利用超标功率曲线净偏差电量自归零能力整定储能设备SOC 或功率基点,并重点对部分非归零成分施加发电控制量,有利于降低EESS 无效调节量和调节次数,提高有限容量的校正效能。另外,在分析EESS 对发电曲线偏差校正效果(generation curve deviation correction effect,GDCE)时,还应考虑EESS 属于一次性大额投资且长期运行的性质,而更关注长时间分布规律对GDCE 的影响。
综上,需从发电曲线偏差考核出发重新审视WPF 配置EESS 的问题。为此,本文基于WPF 超标功率曲线历史数据,挖掘、提取并定义影响GDCE的关键特征,进而建立储能需求与特征间的关系以及兼顾技术经济性能的EESS 容量最优规划模型。
1 发电曲线偏差与校正需求间的关系
受限于风电功率预测精度,WPF 申报的日前计划发电曲线与次日实际发电曲线存在较大差异,如南方电网对WPF 日前预测准确率的要求仅为80%[29]。以往由于新能源渗透率相对较低,电网仅在限风时段对WPF 发电曲线偏差进行考核,而其余绝大多数时段只有功率变化速率限制(分钟级的平滑性要求)。对于未来以新能源为主体的新型电力系统,这种粗放型管理模式难以适应新的挑战,需要将WPF 发电计划曲线纳入电网统一考核体系。当WPF 通过合理配置EESS 等措施确保发电计划曲线高精度执行后,意味着超出允许偏差范围的大幅功率波动事件将被有效滤除,从而使得分钟级的快速功率变化问题随着考核标准的不断严格化、允许偏差范围逐渐缩小而变得不再突出。因此,本文可重点从分析WPF 发电曲线超标偏差功率特性出发,探讨EESS 容量需求问题。其中,本章首先结合某WPF 实发功率曲线偏离日前计划曲线的实例,定性分析影响EESS 校正容量需求的主要特征,并给出容量规划方法的总体思路和原理流程。
1.1 发电曲线偏差对调节资源承担电力电量平衡需求的影响
基于发电计划曲线附加允许偏差范围可以得到正负偏差考核边界曲线。实发曲线超出边界曲线的部分属于超标功率,需应用WPF 自备EESS 加以校正。结合某日计划和实发曲线分析偏差功率的影响,如图1 所示,图中每15 min 为1 个调度时段。图1(a)中的容许区间由正负偏差考核边界形成。图1(b)中的向下校正需求由正向超标电量累积形成,向上校正需求由负向超标电量累积形成,二者之差形成净偏差电量和净校正需求。
净校正需求若不及时处理,将可能在当日结束时累积出较多的考核电量,其值越大,一般预示着对调节资源的需求越大。然而,因向下和向上校正需求事件出现的时机和幅度具有较高的随机性,导致二者以非严格但近似对称的方式交替出现(大致可由图1(b)中净校正需求曲线近似围绕0 MW·h 水平线上下波动看出),从而使得净校正需求量明显小于二者单独校正的需求量。这一效应可视为由净偏差电量的短时自归零特性产生。净校正需求偏离0 MW·h 水平线的幅度,反映电池SOC 偏离基点的时变程度,其数值及其分布规律是考量调节资源承担短期电力和电量平衡需求的关键指标,对合理规划EESS 电量具有引导价值。
1.2 曲线特征对储能容量及其使用实效的影响
充分挖掘和利用好WPF 超标功率曲线关键特征,将有助于提高EESS 规划和使用实效。其中,超标功率幅度和净偏差电量归零度为最主要的特征指标,且前者影响超标事件平均功率水平、后者影响净校正电量大小。
假设为前述WPF 配置10 MW·h 的EESS 用于校正超标功率。结合图1,令初始SOC 为0.5、调控范围为0.1~0.9,则可基于SOC 变化情形分析主要特征对EESS 容量及其使用实效的影响,见图2。

图2 EESS 的SOC变化Fig.2 SOC changes of EESS
一般导致EESS 使用实效降低的两种状态为待机态和失能态。其中,失能态又分为电量裕度耗尽态和容量裕度耗尽态(分别简称为电量失能态和容量失能态)。当处于待机态时,说明当前没有超标事件,无须充放电;当处于失能态时,说明已发生超标事件,但不能按需足额校正,即须放电时SOC 已达下限,或须充电时SOC 已达上限。待机态和失能态均属于非工作态,所占小时数越多意味着EESS 闲置率越高。
下面从两种非工作态形成原因分析曲线特征对EESS 容量及其使用实效的影响。
1)超标功率幅度的影响
综合图1 和图2,当某调度时段出现超标事件时,若超标功率幅度过大,则意味着EESS 进入容量/电量裕度快速消耗的行为阶段。若一段时间内高频次出现大幅度超标事件,特别是同向大幅度超标事件,则EESS 进入失能态的概率和产生高考核电量的风险将显著上升,须增配更大容量EESS 加以校正。反之,当超标事件以低频次或普遍以低幅度出现时,EESS 进入待机态的概率将显著上升,或产生高考核电量的风险将急剧下降,此时需防范因EESS 容量过配引起的回收期过长等问题。上述两种不良倾向均会降低EESS 使用实效,需统筹考虑。
2)净偏差电量归零度的影响
综合图1 和图2,当异向超标事件以近似对称的方式交替出现时,由正负超标事件累积的净偏差电量将呈现较高的短时自归零特性,此时,较高的归零度将使EESS 净校正需求明显降低、正负超标事件自平衡能力明显提高,EESS 进入失能态的概率也会随之下降,其容量可以适度降低以控制投资成本。反之,当持续出现同向超标事件时,意味着净偏差电量失去短时自归零性,SOC 会更快向电量/容量失能态趋近或更长时间处于失能态,此时则须增配更大容量EESS 加以校正。由此可见,净偏差电量归零度的高估和低估倾向,会不同程度地引起EESS 容量欠配和过配问题,应予统筹考虑。
1.3 储能容量规划总体思路与流程
在定性分析了超标功率曲线特征对EESS 容量的影响后,需首先建立GDCE 与曲线特征和储能容量间的量化关系(简称GDCE 模型),才能最终结合经济指标优选出容量规划方案。本文建立GDCE模型、规划EESS 容量的总体思路与流程见附录A图A1。
规划的基础性前期工作为GDCE 模型的建立。为此,首先需从WPF 历史数据中挖掘提取出超标功率曲线主要特征的参数取值范围,并统计不同时间尺度内的特征参数值X1。特定时间尺度内的一组特征参数值X1为一个样本,不同时间尺度对应的样本构成风电功率曲线样本集。其次,将样本集配以不同容量设定值为X2的EESS,并统计分析出GDCE 的期望值Y。如此操作,可以生成反映映射关系(X1,X2)→Y的样本集,并由此通过函数逼近方式建立GDCE 模型Y(X1,X2)。
在完成上述基础性建模工作后,可以将其与储能投资和使用成本等因素综合,最终建立起完整的储能容量规划模型,并由此给出优化规划方案。
2 校正效果模型
本章将建立反映GDCE 与关键曲线特征和EESS 容量间关系的模型。
2.1 超标功率幅度特征
首先,明确偏差考核标准以计算超标功率幅度特征。当沿用中国电网采用多年的按各调度时段Δt=15 min 平均功率核算考核电量时,WPF 实发功率相对计划曲线的超标功率幅度时段指标定义为:

由定义可知,ΔPt≠0 意味着在时段t产生1 次超标事件,超标程度由偏离0 的程度反映。基于此,可考察一定历史数据统计窗口(年或多年)内超标事件的频次及其对应的幅度概率分布情况。
设WPF 历史数据在统计窗口内出现的所有超标事件构成集合Ω(正、负超标事件子集分别为Ω(+)和Ω(-),Ω(+)∪Ω(-)=Ω),超标总次数为NΩ。由此可定义超标事件比和超标电量比分别为:

其中

式中:Nday为统计窗口包含的总天数;NT为每日时段数,取为96;Reve为超标事件数占全部时段的比重;Rene为超标电量占合格计划电量Equa的比重。
在Ω中,设具有不同超标功率幅度ΔP的事件子集所占的密度函数为fΩ(ΔP),则其满足:
式中:Sbas为WPF 额定(基准)容量。
当Reve和Rene低于WPF 设定的期望阈值时,可不考虑配置EESS;当Reve和Rene越高于期望阈值且ΔPsta越大时,说明WPF 发电曲线偏差超标程度越重,对EESS 配置容量的需求越大。
2.2 净偏差电量归零度特征
2.1 节从时段(15 min)和时窗(年)角度分别定义了超标功率幅度时段指标ΔPt和统计指标ΔPsta,且后者的计算需要基于前者提供的信息,其结果将作为边界条件应用于后文EESS 容量规划问题。
由于2.1 节在形成fΩ(ΔP)时,默认各超标事件样本间相互独立,尚缺乏对第1 章分析的净偏差电量短时自归零特性的考虑。为此,从EESS 服务于短期WPF 发电控制出发,定义净偏差电量归零度指标(短时窗指标)Rreg,t(Tw)为:

式中:Nre为1 个短时窗包含的时段数;Tw=NreΔt为短时窗长度;Ebas为设定的EESS 容量基准值。
由式(8)可见,指标针对由时段t开始的短时窗建立,且该时窗至少包含1 个超标事件。该指标的物理含义等效为短时窗内正负偏差电量相互抵消后剩余的净值相对EESS 容量基准值Ebas的比例,其数值越小,说明正负超标事件短时自平衡性越高。
在与建立幅度指标相同的历史数据统计窗口内,设其包含的短时窗(至少含1 个超标事件)集合为Ψ,则在Ψ内,具有不同数值的归零度指标Rreg的短时窗子集所占的密度函数为fΨ(Rreg),其满足:

当Tw不同时,集合Ψ、指标Rreg及其密度函数fΨ(Rreg)的内涵均发生变化。
fΩ(ΔP)和fΨ(Rreg)从超标事件幅度与短时窗内异向超标事件平衡程度两方面共同反映WPF 在统计窗口内的出力不确定性,且其函数关系虽受WPF个体差异影响一般难以统一确定,但具体应用时不强求一定有解析形式,可直接使用统计结果。
由函数fΨ(Rreg) 可计算出集合Ψ的期望值为:

该值被定义为与WPF 实发功率曲线对应的净偏差电量归零度特征(统计指标)。
当Reve和Rene越高于期望阈值且越大时,说明WPF 超标功率曲线的净偏差电量越不易出现短时归零,当EESS 实际参与WPF 发电曲线偏差校正时,在1 个调节时窗Tw结束时,SOC 偏离时窗初始SOC 的程度越厉害。因此,就统计规律而言,指标越大,EESS 容量配置量应越大,且随Tw的增大,EESS 容量也相应增加。
需进一步说明的是,前文建立的幅度指标和归零度指标与常规的WPF 功率预测误差的方差指标相比,很好地滤除了发电曲线允许偏差范围内的误差成分(其对WPF 配置EESS 没有要求)的干扰,并能考虑调节时窗Tw内超标事件间因异向产生的净偏差电量短时自归零效应,可使EESS 容量配置更为精准。
2.3 校正效果模型建立
2.1 和2.2 节分别建立了影响GDCE 的幅度指标和归零度指标,主要用于衡量在没有配置EESS时WPF 实发功率偏离/回归允许偏差范围的行为。在此基础上,定义加入EESS 进行偏差校正后的GDCE 提升幅度指标:
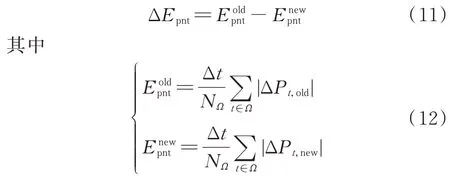
式中:ΔEpnt表示EESS 使超标事件时段偏差降低的平均电量值;ΔPt,old和ΔPt,new分别为EESS 配置前、后在时段t的原始、剩余超标功率。
由于发电曲线偏差考核以超标电量为统计对象,且考核的目的在于严格控制正负超标电量总量,加之考虑EESS 在统计时窗内充放电量(分别对应待校正的正负超标电量)基本相当,故在计算GDCE提升幅度指标时直接采用ΔPt,old和ΔPt,new的绝对值形式。
对特定WPF,因其所处地区气候条件或风力资源固有的分布特性不会在短期(若干年)内明显改变,故可将综合反映2 个特征和EESS 容量Ees影响的GDCE 函数简化定义为:

由前文分析可知,ΔEpnt应与3 个自变量间具有的趋势性变化规律见附录A 图A2。由图A2 可见,ΔPsta和在一定取值条件下,ΔEpnt随Ees单调递增,并满足边界特性:1)当Ees=0 时,ΔEpnt=0;2)当Ees逐渐增加时,预期校正量虽同步增加,但边际效果(灵敏度)却逐渐下降并趋向0(饱和特性)。采用式(14)模拟具有上述边界特性的函数关系:

式中:λ和β为系数,其中λ>0,1 >β>0。
由附录A 图A2 可见,当WPF 拥有更大幅度指标(ΔPsta大)或更小归零度指标(小)时,可在同等Ees条件下取得更高边际校正效果,即灵敏度应更大。相当于在ΔPsta更大和/或更小条件下,λ和β应取更大的值。

考虑到ΔPsta和既可单独也可共同影响λ和β的取值,本文采用式(16)模拟λ和β关于ΔPsta和的函数关系:
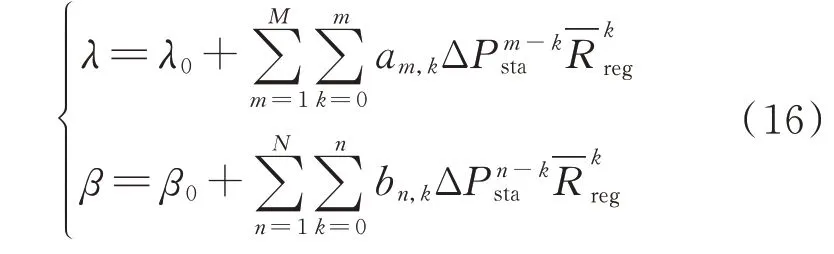
式中:M和N为多项式阶数,实际分析时M和N的取值一般不大于2;am,k和bn,k为各分项系数;λ0和β0为常数项。
将式(16)代入式(14)可得GDCE 模型。实际应用时,基于历史数据统计出ΔPsta和,并在模拟配置多组Ees的条件下评估对应的ΔEpnt。由此可生成一定容量的反映映射关系的样本集。基于该样本集,应用非线性回归方法即可获得模型式(16)中的待定系数am,k、bn,k和λ0、β0。
3 储能容量规划模型
本章首先基于GDCE 模型,分析WPF 超标电量与满足电网统一规定值时的临界EESS 容量(最低要求)的配置关系;然后,建立经济效益模型,并与GDCE 模型、EESS 充放电里程模型(见附录B)综合,给出完整的容量优化规划模型。
3.1 临界储能容量配置关系模型
由第2 章可知,若WPF 超标电量比指标Rene高于自我设定的期望阈值Rene,thr,则可考虑配置EESS;而当Rene高于电网统一规定值Rene,gui时,则必须配置EESS。定义WPF 中确保Rene≤Rene,gui时必须配置的EESS 最低容量为临界容量(记为Ees,gui),具体可由下述关系推出:

临界容量是依据技术标准整定的最低容量,后续考虑经济性规划出的EESS 容量值必须满足Ees≥Ees,gui。设置Rene,gui的出发点在于,未来各区域电网可以综合考虑新能源占比和灵活性资源状况,要求各WPF 结合自身情况合理配置EESS,而不必采取目前依据WPF 装机容量固定比例(如10%或20%等)配置EESS 的一刀切模式。
3.2 经济效益模型
WPF 的收入项为上网电费,支出项为EESS 投资和超标电量考核费。配置EESS 后,WPF 相对于未配置EESS 时的收益增幅,应为集合Ω中因超标事件减轻带来的收益增加值之和ΔF:

式(20)中,当EESS 作用于减轻正超标事件时,收益增加值只有因正超标电量减轻带来的考核减免项;当其作用于减轻负超标事件时,收益增加值除了因负超标电量减轻带来的考核减免项外,还应包括因合格并网电量增加带来的上网费。
就长时窗统计意义而言,校正的正/负超标电量大体相当且约等于0.5NΩΔEpnt,可直接写成:

将其折算成年化收益增加值ΔFyy为:

EESS 的预期使用周期(年)NSL为:

式中:Nmax为EESS 最大循环次数;Euse,yy为年均充放电里程。
由于EESS 为在Tw结束阶段使SOC 回归基点附近实施的充放电行为并未真正校正超标功率,故充放电里程Euse与校正量ΔEpnt并不相等,需单独建立Euse的关系(见附录B),并由此获得Euse,yy。
配置EESS 还须满足WPF 投资收益目标要求:应使WPF 应用EESS 后获得的预期年均收益率μyy≥μmin(最低预期值),即

式中:cb为EESS 单位投资成本。
可推得与μmin对应的EESS 容量Ees,eco为:

经研究发现:Tw为定值时,在现有功率预测水平与储能造价条件下,μyy随Ees(大于Ees,gui)的增加呈单调下降趋势。若μyy(Ees,gui)≥μmin,WPF应优先满足技术约束(子规则1);若μyy(Ees,gui)<μmin,则WPF取不到比Ees,gui对应μyy更高的预期平均收益率(子规则2)。因此,两种情况最优容量Ees(Tw)均取Ees,gui:

子规则1 符合WPF 在满足技术性约束前提下尽可能取更大μyy的诉求;子规则2中仍取Ees,gui是WPF取不到比Ees,gui对应μyy更高预期年均收益率的折中技术选择。于是,可得:

基于所建立的模型,可以获得多个典型Tw条件下的计算结果,详见附录A 表A1。从表A1 第3列μyy数据中选出最大值所在的行(设为g),其对应的Ees,g、Tw,g和μyy,g即为最优容量、SOC最优回归周期和最大预期年均收益率。
3.3 储能充放电功率水平规划
规划EESS 时,除确定容量大小外,还需确定充放电功率水平。本文以控制超标电量未校正率为目标整定EESS 充放电功率水平:

式中:Pe,min为待规划的EESS充放电功率水平;ε为受Pe,min限制未能校正的超标电量比例上限,当充放电功率水平达到Pe,min时,WPF可校正大于(1-ε)×100%的超标电量;分别为因充放电功率水平限制无法校正的正、负向偏差平均功率。
4 算例分析
本章重点开展3 项实验:分析Tw对GDCE 的影响;建立并验证GDCE 模型的有效性;结合经济指标,规划EESS 容量方案。
4.1 场景设置
依托爱尔兰与北爱尔兰EirGrid 系统2015—2019 年期间的实发和预测风电功率数据,等比缩放为100 MW 的WPF。观测5 年数据发现:每年的ΔPsta和统计结果虽有小幅波动,但各年的偏差幅度分布和回归特性近似,故式(13)简化条件成立。
设取Rup=Rdn=0.1、Ebas=10 MW·h、Sbas=100 MW、Tw=4 h。在此条件下,可计算出超标事件比Reve和超标电量比Rene分别为73.728% 和12.182%,以及各年份的ΔPsta和及其逐年累加平均值(见表1)。其中,Ebas、Sbas、Tw、Rup和Rdn均影响ΔPsta和统计结果;Ebas、Sbas、Rup、Rdn为场 景设置边界条件,仅有Tw为待决策变量。
由表1 可进一步计算出幅度指标和归零度指标在4 年内的逐年统计值,相对于5 年累加平均值,最大偏差分别只有4.14%和4.54%。因此,哪怕历史数据只有1 年或2 年,指标最大统计偏差也能控制在百分之几范围内,其对EESS 容量规划和工程预算构成的不确定性应在可接受范围内。故下文仅以5 年平均结果为例进行分析。

表1 WPF 各年指标计算结果Table 1 Calculation results of annual indices for WPF
4.2 Tw对规划容量影响的分析
Tw不同意味着EESS 参与超标功率校正的周期不同。在1个Tw结束时,为维持下一周期的调节活力,应要求SOC 回归基点(如初始SOC 为0.5)附近。Tw的取值将影响ΔEpnt和Euse。假设配置10 MW·h 的EESS,Tw取1~8 h(Δt=0.25 h),Euse和ΔEpnt变化趋势如图3 所示。
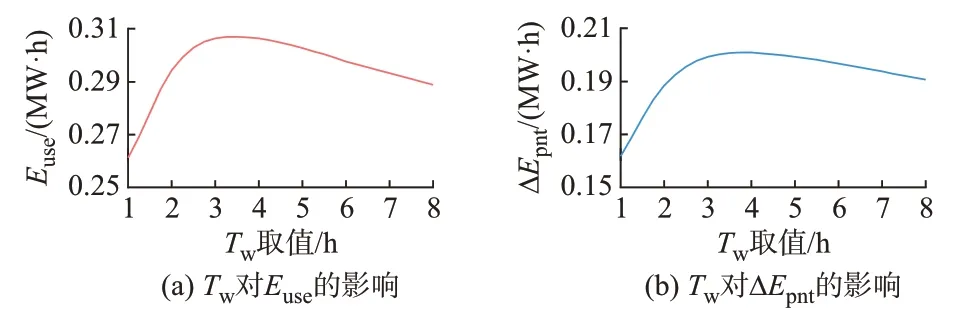
图3 Tw对GDCE 及EESS 充放电里程的影响Fig.3 Influence of Tw on GDCE and charging and discharging mileage for EESS
ΔEpnt和Euse随Tw均呈先增后减趋势。当Tw=3.75 h 时,ΔEpnt达到最大值,即最优调节周期为3.75 h。Tw过小时,小规模EESS无法满足SOC回归基点的需求,过高则导致充放电动作减少;Tw过大时,SOC 回归基点的压力虽变小,但原可通过充放电行为降低电量/容量耗尽风险的时段没有动作,也会导致偏差校正量下降。只有Tw取适当值时,才能利用有限的EESS 校正更多的超标电量。
4.3 模型有效性分析
建立GDCE 模型与EESS 充放电里程模型需首先确定函数形式的最高次幂,M和N分别取1~2且Tw取1~8 h。设置容量取值范围为[5,15]MW·h、优化步长为0.1 MW·h,生成ΔEpnt随不同变化的样本集,以此建立GDCE 模型。
经验证,当M=1、N=2 时,Tw取任意值,整体精度最高且较为稳定,最能反映ΔEpnt、Euse与ΔPsta、间的函数关系。因此,本文最终确定M=1、N=2(M、N取不同值时模型精度见附录A 图A3)。Tw=4 h 时,Ebas取不同值时ΔEpnt、Euse的计算误差如图4 所示(模型中各系数值见附录A 表A2)。

图4 变量域内的误差分布Fig.4 Distribution of error in variable domain
由图4 可见,在变量域内,最大误差和平均误差均处较低水平,即GDCE 模型和里程模型均拥有较高的逼近精度,能够正确反映ΔEpnt、Euse与ΔPsta、间的函数关系。
4.4 储能容量规划结果
设cpnt,up、cpnt,dn、ce、cb、Nmax、μmin、Rene,gui分别 为1 000 元/(MW·h)、500 元/(MW·h)、500 元/(MW·h)、4.00×106元/(MW·h)、5 000 次、10%和7.5%。
首先,考虑约束Rene≥Rene,gui,仍以WPF 的5 年统计结果为例。由于未配置EESS 时,WPF的Rene为12.182%,已超过10%(模拟标准值),故须配置一定量的EESS。对于特定的Tw(仍以4 h 为例),Rene和μyy随EESS 容量的变化情况如图5 所示。
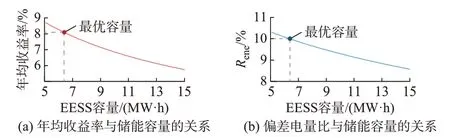
图5 特定SOC 回归周期(Tw=4 h)时的EESS 最优容量Fig.5 Optimal capacity of EESS in specific SOC regression period (Tw=4 h)
由图5 可见:当Tw=4 h 时,Ees=6.4 MW·h 为EESS 最优容量配置方案,此时的预期年均投资收益率为8.089 1%。年投资收益率随EESS 容量的增加而单调下降,这是由于EESS 的闲置率随容量不断增大造成的。因此,仅需配置满足导则要求的EESS,若高于此配置,将影响WFP 经济性。
Tw取不同值时,不同的SOC 回归周期将影响校正效率,因此规划EESS 容量时要同时确定最优SOC 回归周期。不同Tw值对应的最大年均投资收益及最优EESS 容量如图6 所示。

图6 不同Tw下最大年均投资收益率及最优EESS 容量Fig.6 Maximum annual rate of return on investment and optimal capacity of EESS with different Tw
由图6 可见,设置不同的回归周期时,EESS 的最优容量与年均投资收益率均不同。当Tw=3.25 h 时,Ees=6.3 MW·h,年均投资收益率最大为8.140 9%,可认为配置6.3 MW·h 的EESS并以3.25 h 回归周期控制SOC 为最优方案。
最后,确定充放电功率要求。若设置ε=5%,应用式(29)计算得Pe,min=4.573 MW(折合充放电倍率为0.725 9),此功率水平能够保证校正大于95%的超标电量。
当Rene,gui采取不同技术标准时,EESS 最优容量与SOC 最优回归周期也不同,具体见表2。

表2 不同技术标准下的EESS 规划方案Table 2 Planning scheme of EESS with different technology standards
由表2可见,当Rene,gui收紧时,EESS 的容量逐渐增大,SOC 回归周期变长,配置EESS 的投资收益率下降。这是因为标准较低时,仅需校正回归程度较高部分的超标功率即可,且边际校正效益较高;反之,当标准较高时,需要继续校正回归程度较低部分才能达标,导致边际校正效益有所下降。因此,电网在制定关于Rene的运行规范时,需兼顾网侧调控需求和WFP 个体对技术标准的适应能力。
5 结语
在提取WPF 发电曲线超标功率幅度指标和净偏差电量归零度指标的基础上,探讨了EESS 容量规划问题,得出如下结论:
1)对于WPF 超标事件集统计的幅度指标和归零度指标,二者数值越大,用于校正WPF 超标功率的EESS 容量需求越大;
2)所建立的GDCE 模型较准确地反映了WPF超标电量校正程度关于幅度指标、归零度指标和EESS 容量的关系,可应用于EESS 容量规划模型;
3)融合GDCE 模型和EESS 充放电里程模型,计及超标电量比约束和年均投资回报率约束的EESS 容量规划方法,可以计算出技术经济综合性能更优的容量方案;
4)所提出的EESS 容量规划方法能够适应不同严格程度考核标准、不同典型调节周期下辅助WPF跟踪发电计划时的EESS 容量规划需要。
上述方法和结论,可进一步拓展应用于辅助光伏电站跟踪发电计划时的EESS 容量规划问题,以及综合调度EESS 和柔性负荷协同参与跟踪风光场站发电计划时的容量规划问题。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。

