基于耦合特征与多任务学习的综合能源系统短期负荷预测

吕忠麟，顾 洁，孟璐

（上海交通大学电子信息与电气工程学院大数据工程技术研究中心，上海市 200240）

0 引言

综合能源系统（integrated energy system，IES）基于多种能源生产、存储的装置及能量调度管理，能够实现可再生能源的充分消纳和多种能源供需间的灵活转换［1］。准确的负荷预测是IES 安全经济运行与优化管理的基础，考虑到区域型IES 体量较小、负荷波动性强、对短期负荷预测精度要求高，在负荷预测中需要更加注重对数据所蕴含的不同能源负荷间关联关系的充分挖掘和预测技术的提高［2-3］。

近3 年来，针对IES 短期负荷预测也有较多的研究成果发表。文献［4-6］采用如小波神经网络、改进粒子群以及基于注意力机制的卷积神经网络等方法，提高了IES 短期负荷预测的精度和预测效率；文献［7-8］考虑了IES 中不同能源类型负荷间的耦合关系，采用了灰色关联性分析法及Pearson 相关系数，分析了冷热电负荷之间的耦合性并据此构建了预测模型，进而提高了区域型IES 短期负荷预测的精度。这些研究有些将电负荷预测的思路直接移接在IES 冷热电负荷的预测中，没有考虑各负荷间的耦合特征；有些研究虽然考虑了对负荷间耦合特征的挖掘利用，但仅限于利用相关性分析筛选耦合性较强的输入变量，未能实现对耦合特征的提取，也并未直接利用耦合特征对预测模型进行改进。

IES 中由于能源转换设备的存在，使得不同能源类型负荷间存在耦合关联，因此，负荷需求的预测不应是冷、热、电3 种负荷预测的简单叠加，而是需要对不同负荷间的耦合关系进行深入剖析，利用负荷间的耦合性所包含的信息提升模型的预测效果。近年来，越来越多的学者开始意识到该问题中耦合性研究的重要性。目前，IES 负荷预测研究中对耦合效应的刻画方式主要从耦合特征（coupling feature，CF）构建和耦合预测建模两方面展开。

其中，耦合特征构建是指在特征构造阶段考虑能源耦合性，现有研究多通过包括卷积神经网络［9］、长短期记忆（long short-term memory，LSTM）模型［10］等在内的深度学习方式端到端自动构造耦合特征，鲜有从特征工程的角度挖掘负荷之间的耦合性。然而相较于特征工程，基于深度学习的方式所构造的耦合特征有着不具备物理可解释性、与各负荷间的宏观联系对应不够清晰的缺点。对于相互耦合的变量间的特征级分析，在其他领域已初步开展了相关研究，如文献［11］分析了人脑的不同区域在结构和功能上的连通性所造成的神经影像数据间的相互关联，利用耦合特征挖掘算法对不同影像数据间的耦合性进行挖掘，进而提高了脑部神经影像学分类的准确率。

另一方面，耦合预测建模是指在建立预测模型的过程中考虑不同负荷需求间的耦合作用。现有研究主要通过权值共享实现，如文献［12］利用深度置信网络的共享机制细化特征更好地表现各任务间的复杂相关性，提高了IES 负荷预测的效率和精度。文献［13-14］通过多任务学习在预测精度、训练时间等方面获得了较好的预测效果，证明了多任务学习在IES 负荷预测领域的优势。

本文在对现有成果进行分析的基础上，提出了一种融合耦合特征挖掘算法和LSTM 多任务学习的区域型IES 冷热电负荷短期预测模型。首先，该模型利用耦合特征挖掘算法，将冷热电负荷间抽象的耦合关系初步提炼为结构化数据变量；随后，将耦合特征变量、负荷历史数据及温度等作为外生变量输入基于多任务学习搭建的深度学习模型中，通过任务信息共享的方式进一步提取负荷序列间的耦合特征；进而，实现对冷热电负荷间耦合关系的充分挖掘与利用，以此提高了预测精度；最后，本文采用美国亚利桑那州立大学坦佩校区IES 的负荷数据［15］进行了详尽的算例分析，并利用SHAP值［16］对引入耦合特征变量的有效性进行了解释。

1 冷热电负荷序列的耦合特征挖掘

1.1 区域型IES 冷热电负荷耦合特征分析

为量化评估区域型IES 各负荷间耦合特征的强弱，并初步体现本文耦合预测模型的有效性，本节采用统计学方法计算区域型IES 冷热电负荷间的同步系数和互补系数（具体求解流程见附录A），定量描述冷热电负荷之间的耦合程度。

负荷同步系数IT用于描述不同负荷之间的匹配度关系，量化评估负荷间的同步性。IT越接近于0，表明冷热电负荷在所研究的时间尺度内的变化特性越接近，负荷间的耦合程度越高；反之，IT越大，说明负荷的变化特性越不一致，负荷间的相互同步性越差。冷热电负荷受季节因素影响较大，以季为周期，计算冷热负荷、冷电负荷和电热负荷间的同步系数，结果如表1 所示。

表1 冷热电负荷同步系数Table 1 Synchronous coefficients of cooling,heating and electrical loads

由计算结果可以看出，整体上冷电负荷同步系数最小，即同步性更强，这是因为该校区气温较高，电制冷需求大，导致电负荷随着冷需求的提升而增加。同时，冷电负荷同步系数在夏季时最小，而电热负荷同步系数在冬季时最小，这表明其同步关系受季节影响。

负荷互补系数IC用于描述冷热电负荷叠加后的负荷情况，量化评估不同负荷变化量相互抵消的程度。IC越接近于0，表明冷热电负荷在所研究的时间尺度内的变化量抵消越多且越接近，负荷间的互补性越强。以季为周期，计算冷电负荷、冷热负荷、电热负荷和冷热电负荷间的互补系数，结果如表2所示。

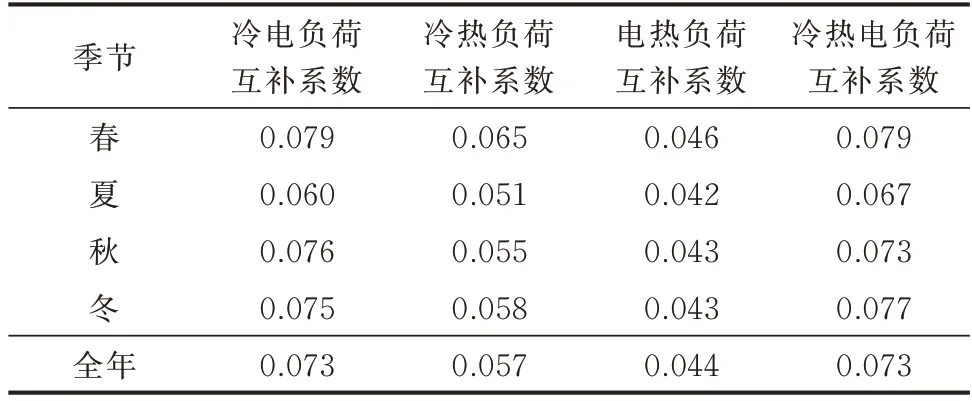
表2 冷热电负荷互补系数Table 2 Complementary coefficients of cooling,heating and electrical loads

由计算结果可以看出，冷热负荷和电热负荷互补系数较小，即冷热和电热负荷的变化呈现出较明显的“反步调”特征。

通过以上IES 冷热电负荷耦合性指标的计算可以发现，冷电负荷的变化趋势存在较明显的同步性，冷热负荷和电热负荷间则存在一定的互补性，表明在预测过程中不同负荷特征可以相互借鉴，从而提升自身的预测效果。

本文后续将从特征工程的角度出发，利用耦合特征挖掘算法将负荷间的耦合特征提取为可直接输入预测模型的结构化数据，以实现对负荷间耦合关系的初步利用。

1.2 冷热电负荷序列的耦合特征挖掘算法

耦合特征是描述不同能源类型负荷间耦合特征的特征变量，负荷间的耦合特征一般包括负荷自身的内耦合性和不同能源类型负荷间的外耦合性。内耦合性通过计算负荷的自相关性得到，而外耦合性则通过计算不同负荷间的相关性实现［17］。

假设有M组样本，将冷、热、电3 种负荷序列分别表示为C、H和P，耦合特征的构造过程如图1所示。

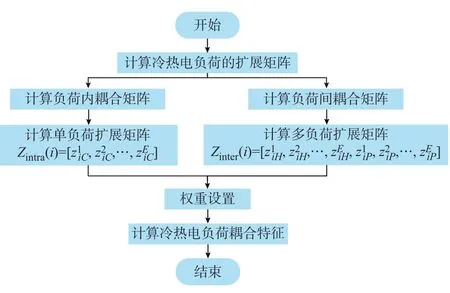
图1 区域型IES 冷热电负荷耦合特征构造流程图Fig.1 Flow chart of coupling feature construction ofcooling,heating and electrical loads for regionalintegrated energy system

对负荷进行耦合特征挖掘的算法由以下5 个步骤组成。

1）计算冷热电负荷的扩展矩阵。在相关性研究领域中，Pearson 相关系数常被用于量度变量之间的相关程度［9，18］，然而，Pearson 相关系数仅能描述两个变量之间的线性关系，而冷热电负荷每对变量间的耦合关系可能包含非线性的部分。因此，本文采用计算负荷变量高次幂的方式将原始数据拓展为更多维度，如式（1）所示，从而使Pearson 相关系数不仅能描述变量间的线性关系，还能描述变量间高次的非线性关系，增强了特征的表达能力。

2）计算负荷内耦合矩阵。结合拓展矩阵，对第j个变量（以冷负荷变量为例），利用自身幂的Pearson相关系数对其自相关性进行建模，如式（2）所示。

3）计算负荷间耦合矩阵。同理，对于第j个变量与其他变量的互相关性（以冷负荷与热负荷为例），利用其自身幂与其他变量不同幂次的Pearson相关系数进行建模，如式（3）所示。

4）计算单负荷扩展矩阵和多负荷扩展矩阵。将拓展矩阵Z的行向量划分为单负荷扩展矩阵和多负荷扩展矩阵，便于后续耦合特征的计算。

冷负荷扩展矩阵为:

冷负荷与其他负荷间的扩展矩阵为:

5）计算耦合特征。任何解析函数都可以用其泰勒展开式来近似，文献［19］提出利用变量值的类泰勒展开来表示耦合关系，其中变量拓展幂之间的Pearson 相关系数起到函数导数的作用，建立基于泰勒级数的耦合特征计算公式如式（6）所示（以冷负荷为例）。

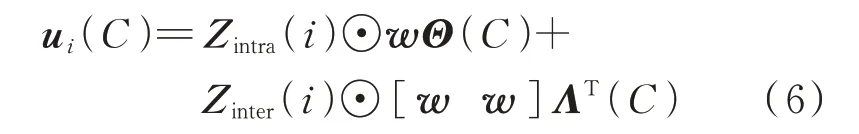
式中:w=[(1/1！)，(1/2！)，…，(1/E！)]为建立类泰勒展开所需的系数矩阵；⊙表示哈达玛积。

对于第i个样本，其耦合特征变量如下:

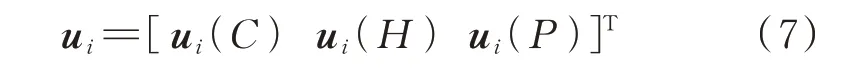
式中:ui(H)和ui(P)分别为第i个样本的热、电耦合特征。

为兼顾负荷间的线性与非线性耦合关系，同时尽量避免过大的计算量，取扩展幂级数为3。将冷热电负荷历史序列输入耦合特征挖掘算法，得到3 种负荷的内耦合及外耦合共计9 个耦合特征CFR1～CFR9 的时序数值，在后续预测建模中可作为预测模型的输入变量，以反映负荷的耦合关系。

耦合特征挖掘算法具有以下优点:

1）计算过程中使用全部数据进行特征构造，可以提高算法的鲁棒性；

2）该算法使用无监督学习构造耦合特征，具有强泛化能力，是对监督学习的有力补充；

3）可以通过设置扩展幂级数的大小，对负荷之间的线性或非线性耦合关系进行挖掘，使用十分灵活。

以美国亚利桑那州立大学坦佩校区IES 的冷热电负荷数据为例，采用上述耦合特征挖掘算法构造该校区每小时冷热电负荷的耦合特征，截取部分计算结果示于附录A 表A1。由计算结果可以看出，冷热电负荷间存在复杂的耦合关系，并与季节、星期、节日及日内作息等因素密切相关，其数值大小在不同的时间周期下呈现复杂的变化规律，仍有待通过深度学习进一步挖掘。

同时可以看出，本文采用的耦合特征挖掘算法提取的负荷间耦合特征是时序的数据列，后续建模预测中可直接将其作为预测模型的输入变量，通过深度学习进一步对各负荷间的耦合特征进行提取。这种方法与基于Copula 函数、Pearson 相关系数等理论的多元负荷相关性分析方法在机制上有很大的不同。

2 基于耦合特征构造与多任务学习的区域型IES 短期负荷预测模型

考虑到冷热电负荷间存在的耦合关联性，可以将不同能源类型负荷的预测视为多个任务，采用多任务学习（multitask learning，MTL）算法设计预测模型的网络结构，充分利用负荷间的耦合关系，以实现区域型IES 负荷的准确预测。

2.1 区域型IES 短期负荷预测模型变量选择

研究成果显示，区域型IES 冷热电负荷水平受时间、温度等因素的影响［20］。因此，在预测模型中引入周期变量、温度及节假日变量以实现对这3 种特性的建模。其中，周期特性包括月份、当月的第几天、当天的第几小时及当天是星期几；温度特性包括每小时的干球温度及露点温度等；节假日特性是指当日是否为法定节假日。

不同能源类型的负荷间存在耦合性。因此，模型的输入还应包括本文第1 章利用耦合特征挖掘算法计算出的负荷耦合特征变量。此外，不同能源负荷的耦合性受到能源价格的影响:IES 主要购入电能和天然气，并通过电制热和电制冷等能源转换设备实现电、气、冷、热负荷间的相互转换。当电价较高时，系统倾向于购入更多天然气，并通过燃气轮机、余热锅炉和吸收式制冷设备等进行冷热电能源联合供应［21］；而当天然气价格较高时，系统则购入更多电能，通过电制冷和电制热设备等进行供冷和供热。因此，应将包含电价和天然气价格等在内的能源价格纳入IES 预测模型的输入变量中。

2.2 区域型IES 短期负荷预测模型

区域型IES 短期负荷预测模型的多任务学习网络采取硬参数共享的结构，包括冷热电负荷共享的隐藏层和各自的输出层。将所有任务输入共享隐藏层，训练后得到一个通用模型ε，模型参数为θε=[θε，1，θε，2，…，θε，L]，其中θε，l代表第l层神经网络的参数，l=1，2，…，L，L为神经网络的层数。这样就学习到了不同任务的统一表示方法，既保留了各任务的有效信息，又降低了过拟合的风险［22］。

在学习过程中，利用以下损失函数对模型参数进行优化:

式中:lt和λt分别为任务t的损失和权重。

考虑到冷热电负荷的时间序列特性，前一时刻的负荷对当前时刻的负荷有较大的影响，选择LSTM 搭建多任务学习的共享层。利用前文提取的耦合特征变量，建立了基于LSTM 和多任务学习（LSTM-MTL）的区域型IES 短期负荷预测模型（CF-LSTM-MTL），模型结构如图2 所示。

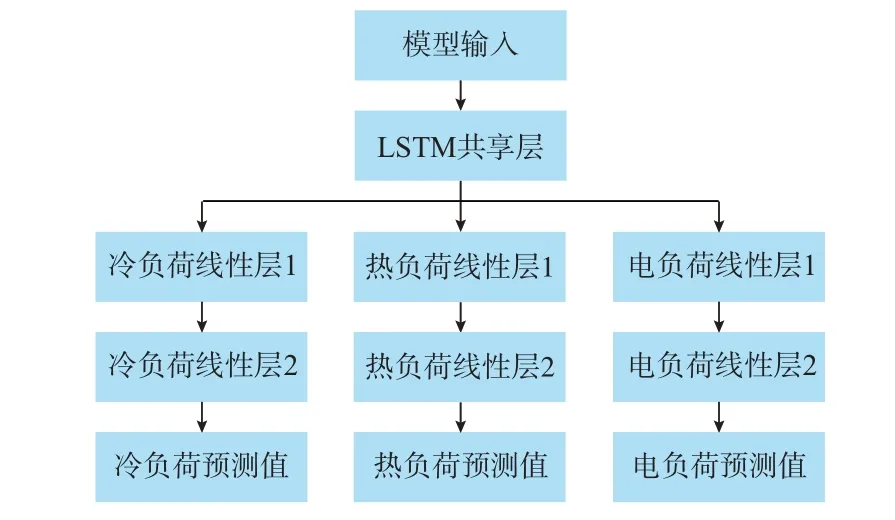
图2 CF-LSTM-MTL 模型结构Fig.2 Structure of CF-LSTM-MTL model

由于LSTM-MTL 模型的训练时间较长，故本文使用离线训练+在线预测的方式，将复杂的模型训练工作限制在离线训练阶段，后续进行实时预测时则无须重新进行训练。首先，基于历史数据离线训练预测模型，再输入实时数据进行在线预测。离线阶段主要是构建耦合特征和通过LSTM-MTL 模型学习温度等输入特征与冷热电负荷之间的关系；在线预测则是将当前时刻的特征输入已训练好的模型快速获得预测结果。

离线阶段模型的训练流程如下:

1）基于耦合特征挖掘算法计算耦合特征变量，作为预测模型输入；

2）根据任务特点等确定学习率、优化器及LSTM 的时间步长等超参数；

3）将多维特征向量作为模型的输入，冷热电负荷值作为模型的输出，自底向上训练模型，直到迭代次数达到预设值或者每次迭代引起的精度改进小于预设值；

4）评估模型的预测效果，本文采用回归模型中常用的平均绝对百分误差（mean absolute percentage error，MAPE）和均方根误差（root mean squared error，RMSE）作为IES 冷热电负荷预测精度的评价指标［24］。

为了对模型多种负荷的预测精度进行整体评价，本文考虑系统内不同负荷的重要性，对不同负荷赋予不同权值，使用多权重的平均绝对百分误差EMAPE和均方根误差ERMSE对模型的整体预测效果进行评价。

式中:EMAPE，C、EMAPE，H、EMAPE，P分别为冷、热、电负荷的平均绝对百分误差；ERMSE，C、ERMSE，H、ERMSE，P分别为冷、热、电负荷的均方根误差；k1、k2分别为将冷、热负荷的单位转换为千瓦时的转换系数；α、β、γ分别为赋予冷热电负荷预测任务的权重，由IES 冷热电负荷水平和负荷特性分析结果共同确定。

5）根据模型学习效果，采用控制变量法确定LSTM 层数、LSTM 层神经元数量及迭代次数等超参数。

包含离线训练和在线预测的区域型IES 冷热电短期负荷预测流程如附录A 图A1 所示。

2.3 基于SHAP 值计算的耦合特征变量引入预测模型的有效性

SHAP 值计算是Lundberg 和Lee 于2017年提出的一种加性特征归因方法［16］。通过分析引入特征变量引起的负荷预测值的变化量，进而分析各特征变量对模型预测结果产生影响的大小，其核心思想是将模型的预测结果解释为二元变量的线性函数:

式中:g(x′)为解释模型输出；f(x′)为原模型输出；Φ0为预测基准值，一般为预测结果的平均值；R为输入模型的特征数量；Φr为第r个特征的SHAP 值；∈{0，1}R为输入特征的二元映射变量，表示样本数第r个特征是否存在。

通过计算本文所提出的区域型IES 负荷预测模型的SHAP 值，可以分析耦合特征变量的引入对预测模型的影响:对于任意样本而言，特征变量是否引入预测模型会对预测结果产生影响，引起预测值变化大的特征变量重要程度高；反之，次要特征变量的引入与否引起的负荷预测结果变化较小。因此，可以根据SHAP 值的大小判断特征变量对模型预测结果的影响程度，进而得出特征变量的重要性。

3 算例分析

3.1 数据介绍

以美国亚利桑那州立大学坦佩校区IES 的数据为例，对本文提出的CF-LSTM-MTL 模型进行应用验证。选取该数据集中2019 年1 月1 日00:00—2020 年7 月15 日23:00 的冷热电负荷数据，并从气象数据网站上下载对应时段的小时级温度数据［25］，按照70%、15%和15%的比例划分训练集、验证集与测试集，由于该IES 中冷、电负荷水平占比高，热负荷占比低，设置冷、热、电负荷的权重分别为0.4、0.2 和0.4。在Keras 框架下搭建LSTM-MTL 网络，用于测试本文建立的预测模型。所有实验在Intel Core i7 CPU 平台完成。

3.2 超参数设置

目前，深度神经网络超参数选取尚无完善的理论指导，需要根据模型的学习效果定值。为获得深度学习模型的最优结构，本文研究采用控制变量法，兼顾模型预测精度与模型复杂度对LSTM 层数、神经元数量和迭代次数等超参数进行选择。

分析LSTM 层数对模型预测效果的影响如表3所示。随着LSTM 层数增加，网络参数成倍增加，模型整体的加权MAPE 也由于过拟合等原因随之增加，模型学习效果变差，故将模型中LSTM 层数定为1。

表3 LSTM 层数对模型预测精度的影响Table 3 Influence of LSTM layers on model prediction accuracy

分析LSTM 层神经元数量对模型预测效果的影响如表4 所示。随着LSTM 层神经元数量的增加，模型参数数量快速增长，模型整体的加权MAPE 先降后升，神经元数量为32 和64 时模型精度相差不大，但是前者对应的模型参数更少，网络结构更简单，计算效率更高，故将LSTM 层神经元数量定为32。

表4 LSTM 层神经元数量对模型预测精度的影响Table 4 Influence of number of neurons in LSTM layers on model prediction accuracy

控制LSTM 层数和神经元数量不变，改变迭代次数，分析模型精度的变化如表5 所示。随着迭代次数的增加，冷负荷和电负荷预测误差先以较快的速度减小，之后在较小的范围内波动，而热负荷的预测误差则先减小后增大，3 种负荷的误差最小值出现的时间不完全同步。

表5 迭代次数对模型预测精度的影响Table 5 Influence of iteration times on model prediction accuracy

为评价模型预测冷热电负荷的综合效果，仍以加权MAPE 作为衡量标准。由表5 可知，当迭代次数为750 时，加权MAPE 最小，模型综合预测效果最佳，故确定迭代次数为750，其他参数设置见表6。

表6 CF-LSTM-MTL 模型超参数设置Table 6 Hyperparameter settings of CF-LSTM-MTL model

3.3 预测结果对比分析

将本文提出的CF-LSTM-MTL 模型与多组对照模型进行冷热电负荷预测效果的对比，比较建模过程中是否考虑耦合特征变量、是否使用多任务学习的预测结果的差异，以验证本文所提模型在区域型IES 负荷预测场景中的优越性。

对照模型包括:

1）基于LSTM 模型对3 种负荷分别预测（SingleLSTM）；

2）基于LSTM 和MTL 建立多输出模型对3 种负荷耦合预测（LSTM）；

3）计及耦合特征变量，基于LSTM 分别对3 种负荷进行预测（CF-LSTM）；

4）计及耦合特征变量，基于LSTM-MTL 建立多输出模型对3 种负荷耦合预测（CF-LSTMMTL）。

为保证实验公平，各模型均使用相同的数据集进行训练及预测，截取部分预测结果的对比见图3（完整预测结果见附录A 图A2），计算各种模型在测试集上的MAPE、RMSE 指标，如表7 所示。

表7 区域型IES 冷热电负荷多任务学习模型和单任务学习模型预测精度Table 7 Prediction accuracy of multi-task learning model and single-task learning model of cooling,heating and electrical loads for regional integrated energy system

图3 区域型IES 冷热电负荷预测结果Fig.3 Prediction results of cooling,heating and electrical loads for regional integrated energy system

预测结果表明:

1）从模型的预测结果可以看出，负荷真实值曲线有明显的峰谷值，波动范围广、波动频率高，而SingleLSTM 预测值曲线变化趋势非常平缓，与负荷真实值曲线有较大的偏差。负荷波动性较强是区域型IES 的固有特性，因此，不能学习到这种波动性的SingleLSTM 模型显然不能满足IES 短期负荷预测需求。

2）区域型IES 冷热电负荷间存在较强的耦合关系，因此，建立的多输出模型的LTSM 耦合预测相较于单独预测的SingleLSTM 模型加权误差明显更小，表明对区域型IES 冷热电负荷的耦合建模有效提升了模型的预测精度。这是因为耦合建模使得不同能源类型的负荷预测过程可以相互学习提取到优良特征，同时，共享的LSTM 层可以提取到负荷间的耦合性，并以高维特征的形式传递到全连接输出层，对冷热电负荷间耦合性的学习是提升IES 负荷预测的有效方式。另外，从单一能源类型负荷预测精度的变化来看，经过耦合建模精度提升最多的是冷负荷，说明在建模过程中，冷负荷从其余负荷处获取了更多高质量的辅助信息。

3）在考虑IES 各负荷间耦合关系建立耦合预测模型的基础上，CF-LSTM 模型引入耦合特征变量后，预测精度进一步提高。同时，耦合特征变量改进了深度学习模型所提取特征的不可解释性，是对耦合建模过程的有力补充。

4）综合上述两种改进思路建立的CF-LSTMMTL 模型兼顾了两者的优点，这种预测模型既能充分挖掘和利用负荷间的耦合关系，又保留了冷热电负荷各自的特性，故预测结果更优。同时，对冷热电负荷的耦合预测避免了对3 种负荷分别建模，简化了建模工作，具有更优的工程应用价值。

基于上述CF-LSTM-MTL 模型预测结果，求解各特征变量加入模型的冷热电负荷加权SHAP值，赋权参考前文，分别为0.4、0.2、0.4，计算结果如图4 所示，图中展示了各特征变量的重要性排序结果。

图4 冷热电负荷特征变量的加权SHAP值Fig.4 Weighted SHAP values of feature variables of cooling,heating and electrical loads

由图4 可以看出，耦合特征CFR8、CFR4、CFR2 和CFR1 的SHAP 值排在较前位置，仅位居小时变量、电负荷历史值、冷负荷历史值和月份等重要特征之下，表明这些耦合特征对模型预测结果有较大的影响。加权SHAP 值的计算结果验证了所提取出的耦合特征对于区域型IES 负荷预测的有效性。

4 结语

本文考虑了区域型IES 冷热电负荷之间的耦合特征，采用基于LSTM 的多任务学习模型，将多用于处理分类问题的耦合特征挖掘算法融入负荷预测中，提出了一种区域型IES 冷热电短期负荷预测模型。首先，采用耦合特征挖掘算法初步提取耦合特征变量；然后，通过多任务学习进一步挖掘负荷间的耦合特征，弥补了目前IES 预测领域对负荷间耦合特征挖掘和利用不足的问题，提高了预测精度；最后，通过分析SHAP 值计算结果证明了预测模型引入耦合特征变量的有效性。本文主要得到如下结论:

1）区域型IES 冷热电负荷间存在明显的耦合关系，在特征工程阶段利用耦合特征挖掘算法提取的耦合特征变量是时序的结构化数据，可与负荷历史数据、日期、温度等外生变量一同作为神经网络模型的输入，实现对冷热电负荷间耦合关系的初步挖掘和利用。同时，耦合特征变量的构建也是对深度学习模型特征提取过程不可解释性的有力补充。

2）本文采用的多任务学习模型包含共享层和冷热电负荷各自的输出层，既可以使冷热电负荷预测任务相互借鉴其余任务的优异特征，又保留了各自的特征，相比于对各负荷进行单独预测，能够更好地学习到区域型IES 各负荷的波动性。

3）由算例分析结果来看，本文综合考虑区域型IES 冷热电负荷的耦合特征及气象、日期等因素的影响，构建的CF-LSTM-MTL 预测模型能够充分发挥耦合特征挖掘算法和多任务深度学习各自的优势，提高区域型IES 冷热电负荷短期预测的精度。

随着IES 的不断发展和能源生产消费逐渐市场化，亟须实现更加实时、准确、可靠的用能预测，而区域型IES 体量较小、负荷波动性强、负荷间耦合性强，在今后的研究过程中应更加注重通过提高预测技术及对数据中蕴含信息的充分挖掘，以实现负荷预测精度的进一步提高。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。