基于分段频率变化率的风电机组一次调频控制策略

2022-06-09 01:20单煜周昌平刘瑞煦梁丹琦

电力系统自动化 2022年11期

单煜，汪震，周昌平，刘瑞煦，梁丹琦

（浙江大学电气工程学院，浙江省杭州市 310027）

0 引言

以推动“碳达峰、碳中和”为契机，加快调整优化能源结构，以新能源为主体的电力电子设备大量接入电网，其有功功率-频率解耦的控制特性使未来电力系统逐渐演变为新能源高渗透的低惯量电力系统［1］。

为有效解决负荷突变引起的频率快速跌落问题，许多学者开始在风电机组层面探究风电机组参与系统一次调频的控制策略，通过在风电并网系统中利用风电机组电力电子接口设备的快速动态响应进行功率补偿参与一次调频。主要的调频策略包括综合惯性控制［2-4］、短时功率增发控制［5-7］、虚拟同步机控制［8］以及功率备用控制［9］。

综合惯性控制能够提高系统对频率的调节能力，为使风电机组具有持续调频能力，风电机组可采用降载运行方式提供功率储备，但为了兼顾调频需求和经济性，降载运行更适用于高风速机组，风电场中风电机组大部分以中低风速运行时难以参与调频［10］。同时，综合惯性控制涉及一次调频后的转速恢复过程，此过程吸收有功功率，将引发系统频率二次跌落［11］。另外，综合惯性控制动作具有自发性，不能作为主动控制手段。

相较于综合惯性控制，短时功率增发控制能人为设定功率参考值，调频更具主动性。文献［5］利用阶梯式惯量控制，有效减小最大频率变化率（rate of change of frequency，ROCOF）和频率偏差，但该策略在阶段切换时会引起巨大的频率二次跌落。对此，文献［6］提出通过斜坡过渡的控制策略，并利用粒子群算法求解参数，有效减小了调频和转速恢复阶段切换过程的功率偏差，但增发功率仅与风速有关，不能根据功率缺额释放。文献［7］提出基于跟踪曲线的短时功率增发控制，在风电机组转子侧变流器加入有功增量，以降低转速移动工作点，从而减小功率输出，削弱切换过程的频率二次跌落，然而该策略调频和转速恢复阶段时间长，不适用于功率波动频繁的场景。

考虑到实际系统中的复杂工况，有部分研究提出了基于频率信号的自适应控制方案，如文献［12］较早提出基于分段控制的风电有功功率-频率控制，通过频率分段使风电机组运行在不同的有功控制区间；文献［13］根据频率阈值分3 个阶段依次启动陆上电网电源、网侧电压源型换流器（VSC）和海上风电场侧VSC 以提高经济效益。文献［14］还进一步考虑ROCOF 的大小和方向变化以加速调整低频降载启动时间和降载幅度，提高频率紧急控制效果。

本文提出一种基于分段ROCOF 的双馈风电机组一次调频控制策略。首先，利用ROCOF 预估频率恶化程度，建立基于分段ROCOF 的风电机组一次调频自适应控制规则，基于不同ROCOF 区间采用变下垂综合惯性控制、改进短时功率增发控制及两者的递增转速恢复，提升风电机组调频适应能力。其中，变下垂综合惯性引入变系数实现自适应控制、改进短时功率增发控制通过集中控制实现风电场有功指令分配，利用本地初始ROCOF 预估功率不平衡量，设计功率整形函数主动响应频率事件；最后，建立含双馈风电机组的四机两区域模型，验证所提策略的有效性。

1 基于综合惯性控制的风电机组调频策略

图1（a）所示为包含综合惯性和转速恢复的风电机组控制框图，在最大功率点跟踪（MPPT）模式的基础上引入综合惯性模块，包含惯性模拟和下垂控制两个环节实现风电机组辅助调频，具有模拟同步机惯性特性以增加系统等效惯量和同步机一次调频提高频率最低点fnadir的优点［11，15］。图中:T1为时间常数；f为频率；Δf为频率偏差。

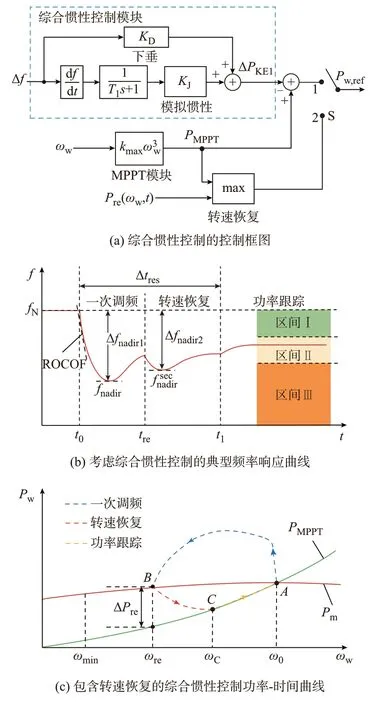
图1 风电机组的综合惯性控制策略Fig.1 Integrated inertial control strategy for wind turbines

图1（b）所示为典型的考虑风电机组综合惯性控制的频率响应曲线［11］，图中:t0、tre、t1分别为调频初始时刻、转速恢复时刻和功率跟踪时刻；fN为系统额定频率。图中可引出6 个频率响应特征量化指标:1）ROCOF；2）频率最低点fnadir；3）二次跌落最低点；4）最大频率偏差Δfmax=max(Δfnadir1，Δfnadir2)，其中Δfnadir1=fN-fnadir，Δfnadir2=fN-；5）稳态频率误差Δfst；6）一次调频响应时长Δtres=t1-t0，Δtres表示频率事件后风电机组参与辅助调频至工作点重新回到跟踪曲线的时间，其值越大则说明控制策略的响应周期更长。

如图1（a）所示，为恢复综合惯性的释放转子动能，风电机组调频控制环还可包含转速恢复环［16］，即在综合惯性控制模块的基础上加入转速恢复模块。转速恢复过程通常包含3 个阶段，如图1（c）所示。图中:Pw为风电机组的输出功率；ω0为风电机组初始运行点对应的初始转速。

1）一次调频阶段（A→B）:综合惯性控制动作过程，功率缓慢下降，该过程图1（a）中开关S 置于1。考虑到转速侧面反映了风速变化，本文采用基于转速变化的分段变下垂控制适应风速差异［3］，表达式如下:

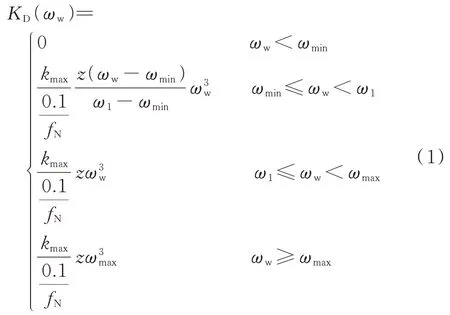
式中:KD(ωw)为风电机组转速为ωw时的下垂系数；kmax为MPPT 系数；ω1为转速的设定值；ωmin和ωmax分别为风电机组正常运行的最小、最大转速，本文设置ωmin=0.7 p.u.；z为比例系数，其物理意义为频率偏差为0.1 Hz 时风电机组增发功率ΔPKE1与PMPPT的比值，其中，MPPT 模式下风电机组的功率。

2）转速恢复阶段（B→C）:当参考功率Pw，ref小于机械功率Pm时，风电机组进入转速恢复阶段，图1（a）中开关切换至2，转速恢复模块动作。此时，若瞬时减小风电机组的输出电磁功率将引起如图1（b）所示的频率二次跌落。在转速恢复阶段，在特定转速范围内根据转速和时间变化采用如式（2）所示平滑转速恢复策略来调整功率参考值Pre(ωw，t)［17］:

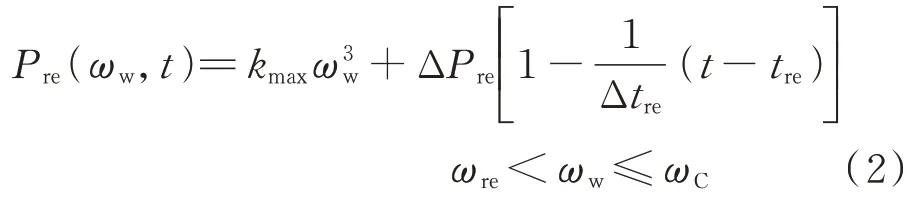
式中:ωre和ωC分别为转速恢复时刻tre和风电机组切换为MPPT 模式时风电机组的转速；Δtre为转速恢复阶段时长；ΔPre为转速恢复阶段的减发功率，ΔPre=Pw，ref(ωre)-PMPPT(ωre)。

3）MPPT 阶段（C→A）:根据图1（a），当PMPPT满足式（3）时，风电机组功率随转速上升直到输出功率回到MPPT 工作点。

文献［18］指出，系统中存在负荷频繁投切、负荷波动、风速变化引起的风电机组输出功率随机波动等不同大小和时间尺度的功率不平衡问题。为了应对高风电渗透率系统中复杂的工况变化，上述综合惯性控制无法完全满足不同功率波动下的一次调频控制策略需求。因此，文中将基于风电机组参与调频系统的ROCOF 特性，提出一种风电机组一次调频控制策略，提高风电机组支持电网调频控制的适应能力。

2 基于ROCOF 的风电机组一次调频控制

2.1 ROCOF 与功率缺额的关系

风电机组利用综合惯性参与调频后，系统的动态响应方程等效为［15］:

式中:HS为系统等效惯性时间常数，满足HS=HG(1-p)［19］，其中，p为风电渗透率，在本文中定义为风电场投入容量SW与系统总投入容量SB之比；HG为同步发电机组等效惯性时间常数［20］；DS为等效阻尼系数；PGi和PL分别为同步发电机i和负荷的功率；KJ和KD分别为风电机组综合惯性控制的虚拟惯性系数和下垂系数。

将式（4）进行线性化，考虑功率不平衡量ΔPunb，可得系统初始ROCOF 为:

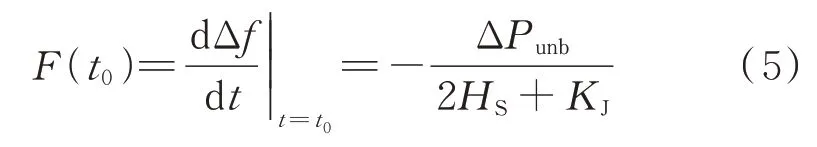
式中:F(t0)为系统在t0时刻的ROCOF，与ΔPunb成正比，故可根据上式将ROCOF 划分为不同区间，采用特定的控制策略实现风电辅助调频的优化。

2.2 ROCOF 变化区间的确定原理

1）dΔf/dt与Δfst的关系

由于Δfst为滞后指标，不能及时反映系统缺额大小，故需要利用其与ROCOF 的对应关系，将区间映射至ROCOF 下。由于系统的等效阻尼与等效调差系数的倒数不在同一数量级，假设稳态时功率不平衡量由同步发电机组承担，其有功出力增量ΔPG为:

式中:RS为系统的等效调差系数，满足RS=RG/(1-p)［19］，其中，RG为同步发电机组等效调差系数。

根据式（6）可得:

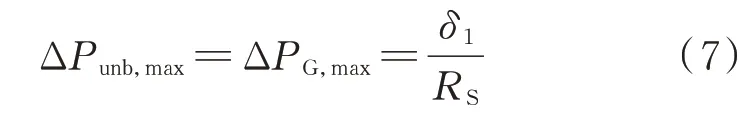
式中:ΔPunb，max为临界功率不平衡量，其物理意义为系统稳态频率偏差为δ1时对应的功率偏差；ΔPG，max为同步发电机有功出力的最大值。

将式（7）代入式（5）可得ΔPunb，max对应的初始ROCOF的绝对值F1为:

2）基于F(t0)的频率分区

由上述分析可知，可将频率稳态偏差区间映射至ROCOF 上，同样可分为3 个区间，在有名值下满足:

（1）区间Ⅰ:0 ≤|F(t0)|＜δ0/[(2HS+KJ)RS]；

（2）区间Ⅱ:δ0/[(2HS+KJ)RS]≤|F(t0)|＜δ1/[(2HS+KJ)RS]；

（3）区间Ⅲ:|F(t0)|≥δ1/[(2HS+KJ)RS]。

在实际电网运行中只要运行方式确定，系统参数在短期内将不发生变化，在故障发生前可在线评估得到［22］，从而基于不同的频率响应区，采用相应的调频策略实现风电机组参与调频的优化。

2.3 基于ROCOF 的控制策略

为了满足针对不同功率不平衡量的调频控制需求，本文提出如图2 所示的一次调频控制，包含综合惯性控制模块、改进短时功率增发控制模块以及转速恢复模块。其中，转速恢复模块为前两者的公用模块。控制策略输出的参考有功功率Pw，ref与无功功率Qw，ref经矢量控制得到转子dq轴电压参考值vrd，ref和vrq，ref，产生空间矢量脉宽调制（SVPWM）信号控制风机转子侧变流器。

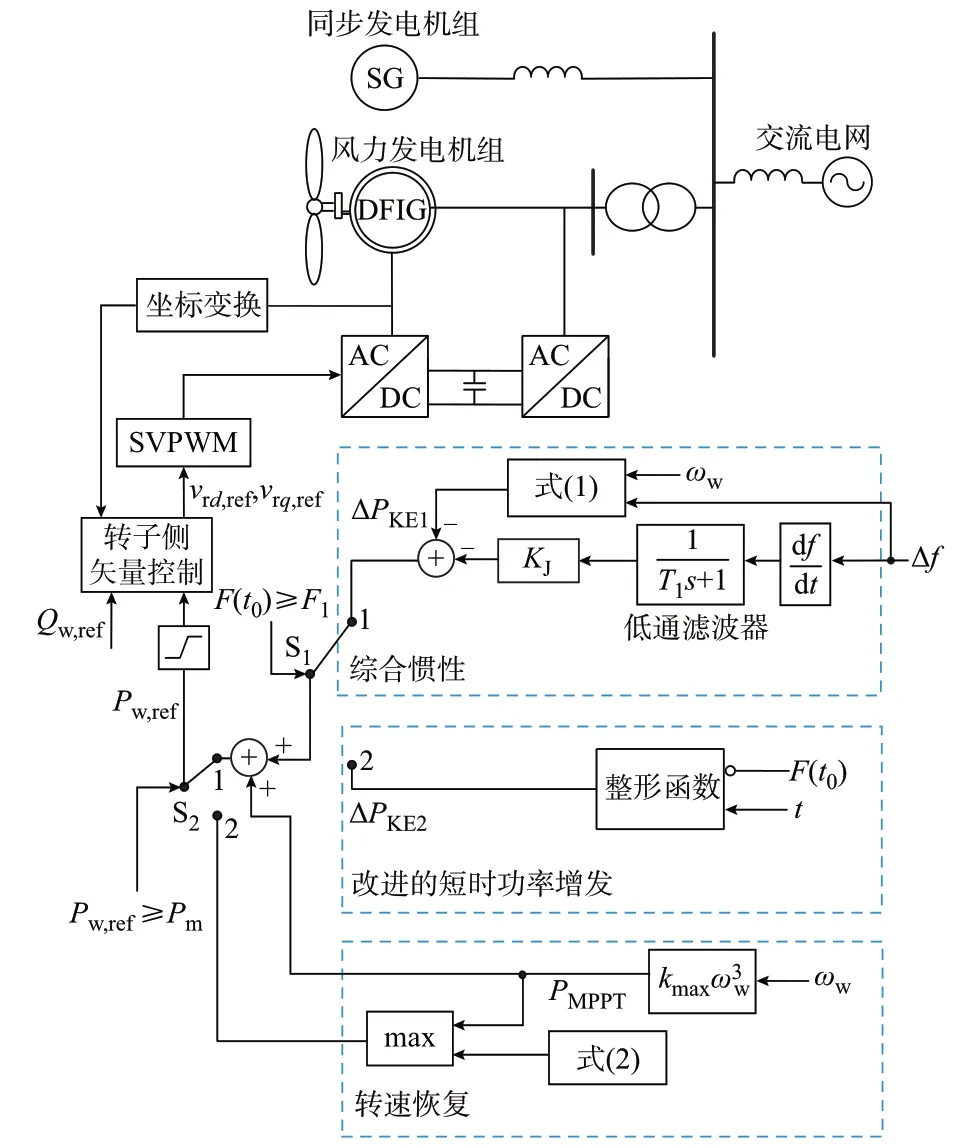
图2 基于ROCOF 的风电机组调频控制策略Fig.2 Control strategy of wind turbine for frequency regulation based on ROCOF

各控制策略对应ROCOF 区间及主要作用如表1 所示，不同频率响应区对应的控制策略如下:

表1 ROCOF 区间设置原则Table 1 Segment setting principle of ROCOF

1）当F(t0)在区间Ⅰ时，综合惯性控制模块启动；

2）当F(t0)在区间Ⅱ时，使用综合惯性控制模块，在满足退出调频条件后，转速恢复并转入MPPT 模式；

3）当F(t0)在区间Ⅲ时，切换为改进短时功率增发控制模块，并与转速恢复模块配合。

2.4 基于ROCOF 的改进短时功率增发控制

2.4.1 控制策略设计

基于ROCOF 的改进短时功率增发控制如图2所示，输入为初始ROCOF 以及变化时间t，经整形函数得到的输出为增发功率ΔPKE2。

整形函数为一个按照时间的分段函数，即

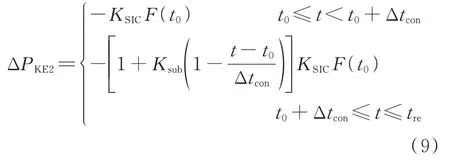
式中:KSIC为增发功率系数；Ksub为减功率系数，令Ksub=Δtcon/(Δttotal-Δtcon)，其中，Δtcon为恒功率阶段时长，Δttotal为ΔPKE2下降至0 的总时长。

为了利用本地量测估计惯性中心频率，可利用文献［23］提出的测点频率法得到。考虑到一阶惯性环节在滤除高频噪声的同时可能发生F(t0)延时，将在研究中采用ROCOF 峰值逼近法来估计F(t0)，具体原理见附录A。

2.4.2 控制效果

在上述短时功率增发策略作用下，与转速恢复模块配合，风电机组状态将经历如图3 所示E→A→B→C→D→E阶段。

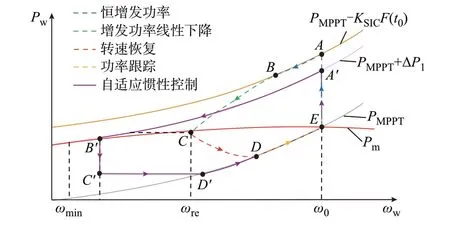
图3 改进短时功率增发控制功率-转速曲线Fig.3 Power-rotor speed curves of improved short-term power over-generation control

假设初始时刻风电机组运行状态位于E点，当风电机组接到增发控制指令时，风电机组功率将经历如下状态演变过程:

1）恒增发功率阶段（E→A→B）:此阶段风电机组增发功率按式（9）第1 行表达式计算，随着转子动能的释放，风电机组总功率因转速减小而下降；

2）增发功率线性下降阶段（B→C）:此阶段补充在恒增发功率阶段后，增发功率ΔPKE2按式（9）第2 行表达式线性下降以缓解频率二次跌落和转速恢复慢的问题；

3）转速恢复（C→D）:当风电机组输出功率下降至满足Pw，ref＜Pm到达tre时刻，风电机组退出调频并按式（2）进行转速恢复。

4）MPPT 阶段（D→E）:转速恢复阶段至满足Pre＜PMPPT后风电机组进入MPPT 阶段。

对比现有的短时功率增发控制，改进策略优点如下:

1）传统的短时功率增发控制通常在恒功率阶段预设增发功率，当发生频率变化超过阈值时启动［5］，响应具有延时且增发功率与功率缺额无关。因此，利用ROCOF 作为触发条件，并利用其估算调频容量需求可加快主动响应速度，合理确定风电机组增发功率。

2）文献［7］提出的自适应惯性控制的功率变化曲线如图3中E→A′→B′→C′→D′→E阶段所示。当有功功率参考值Pw，ref与机械功率Pm相交时，瞬间减小功率进入转速恢复阶段，这导致转速恢复慢、频率以及二次跌落大等问题。在恒功率阶段和转速恢复阶段间引入有功衔接阶段能防止功率突变，缓解频率二次跌落幅度［24］。

2.4.3 风电场的协调控制

针对风电场中各风电机组可用旋转动能差异，需对式（9）得到的功率增量ΔPKE2在风电场中n台风电机组间按可用旋转动能比例进行分配。

设第i台风电机组初始转速为ω0，i，每台风电机组和整个风电场可用旋转动能EA，i和EA分别为:

式中:Hw为风力机惯性时间常数；并令参与系数qi=EA，i/EA。

考虑到风电机组瞬时增发功率不超过额定容量的20%，且存在功率上限，可根据式（11）确定第i台风电机组的功率调整量ΔPKE2，i:

式中:P0，i为初始转速为ω0，i时对应的功率。

风电场层的控制框架如图4（a）所示，通过协调控制，不仅能更精准地满足功率需求，防止过调和欠调的发生，还能进行合理功率分配，减少风电机组失速风险。

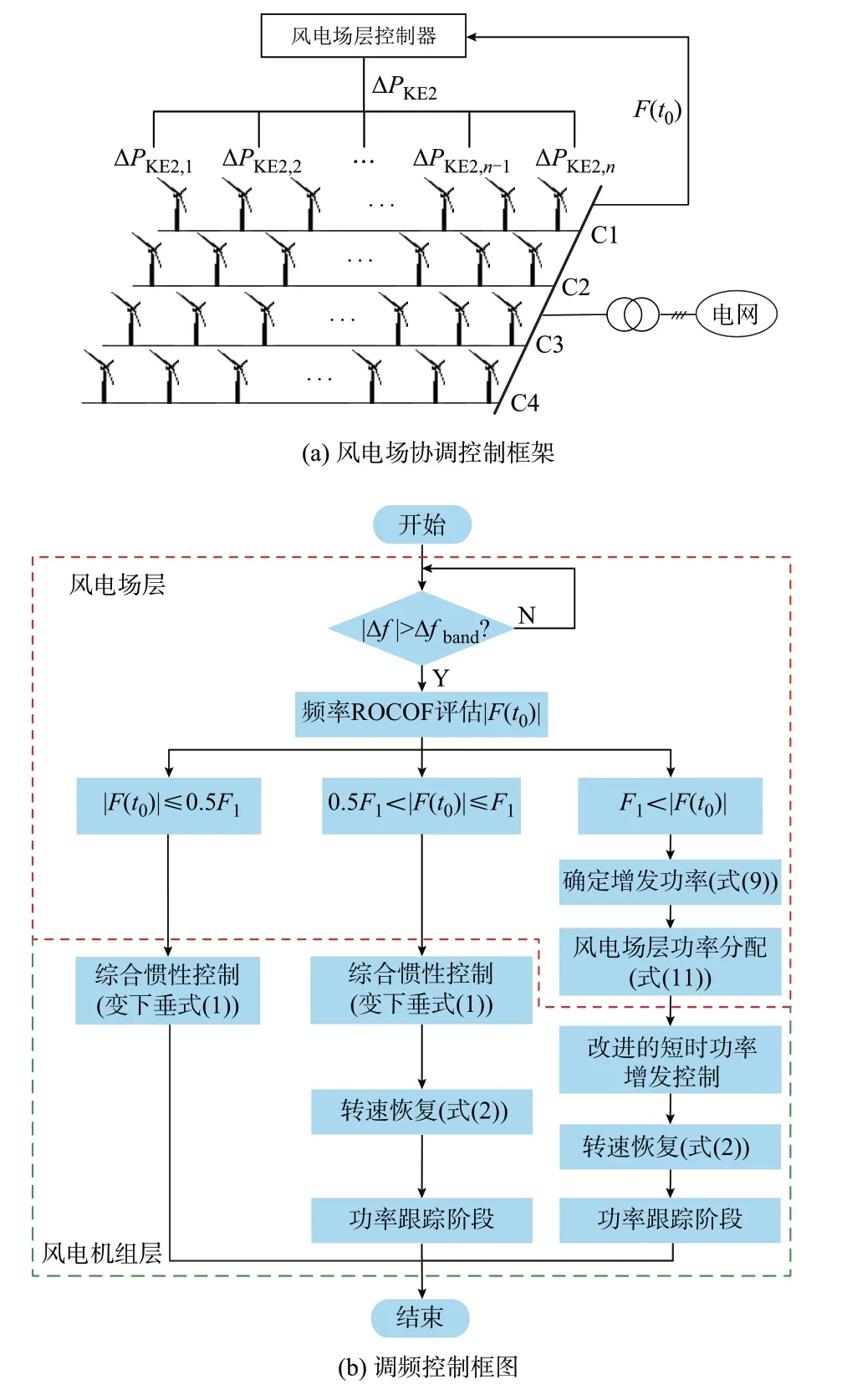
图4 基于分段ROCOF 的风电机组一次调频控制Fig.4 Primary frequency regulation control of wind turbine based on segmented ROCOF

3 风电机组一次调频控制设计

在风电场实际运行中，考虑到风电机组可用调频容量受运行工况影响，考虑通过部分风电机组主动降载为一次调频做准备；同时为避免风电机组频繁动作，通过设置调频死区与ROCOF 动作判据配合。以下对一次调频准备以及整体流程进行说明。

3.1 风电机组一次调频准备

风电机组降载采用经典的定比例备用持留方式，降载后功率Pde为:

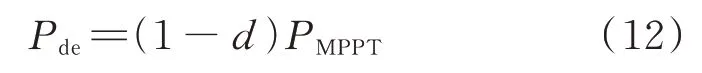
式中:d为降载系数，通常设置为10%～20%［25］。上述风电机组降载可通过超速和变桨控制实现运行工作点偏移［9］。

3.2 调频控制流程

基于ROCOF 的频率控制整体流程如图4（b）所示，具体步骤如下:

步骤1:死区判定。判断系统频率偏差的绝对值|Δf|是否大于死区范围，其中设定调频死区Δfband=0.03 Hz:若是，则继续其余步骤，否则不参与调频。

步骤2:基于ROCOF 的一次调频控制。测量频率ROCOF值F（t0），根据表1 所示ROCOF 区间规则选择切换第1 章及2.4 节提及的控制策略。

4 算例分析

本文建立改进的四机两区域系统验证基于ROCOF 的风电机组一次调频控制策略的有效性，拓扑结构及具体参数见附录B。系统含有4 台同步发电机，额定容量均为100 MV·A，HG=6.5 s；风电场由100×1.5 MW 的双馈风电机组构成，风电渗透率为27.27%，额定风速为12 m/s，通过1 台升压变压器经母线10 接入该系统。风电场布局如图4（a）所示，各行等值风电机组编号为C1 至C4 并考虑风电机组尾流效应［26］，所有风电机组的具体电气参数见文献［27］，其中，前排风电机组（C1）工作在降载模式，降载系数d=10%，其余风电机组工作在MPPT 模式。风电机组主要调频控制参数见附录C，其中综合惯性控制中虚拟惯性系数选用文献［2］设置。根据式（8）计算得F1=0.244 Hz。结合2.2节ROCOF 分段原则，具体阈值的计算结果及设定值（四舍五入）见附录A 表A1。

为了验证所提方法的有效性，分别对比以下两种策略:本文所提控制策略与和文献［7］所提自适应惯性控制（风电机组功率变化轨迹见图3）。研究中考虑如下系统工况变化:当t=10 s 时，负荷突增5%；当t=50 s 时，负荷进一步突增10%。相关仿真结果在图5（a）至（d）中给出，用于比较不同方法的频率恢复效果。另外，表2 还给出了最大频率偏差Δfmax和一次调频响应时长Δtres的计算结果。

由图5（a）可知，在前后两次负荷突增下，系统初始ROCOF（|F(t0)|）分别处于区间Ⅱ和区间Ⅲ，依次启动了综合惯性和改进短时功率增发控制。由图5（b）可知，在频率跌落较小时（首次5%负荷突增），相比风电机组无调频能力场景，两种方法都能较好抑制频率跌落；频率跌落进一步增大时（后续10%负荷突增），本文提出的方法抗频率扰动能力更强、频率跌落更小。从图5（c）至（d）亦可看出，在后续10%负荷突增条件下，由于本文方法可提供更多的增发功率（ΔP），使得频率跌落更少，从表2 中Δfmax计算数据也进一步验证。此外，表2 中显示本文方法的一次调频响应时长Δtres更短，有利于转速快速恢复。

图5 不同负荷扰动下的系统响应曲线对比Fig.5 Comparison of system response curves with different load disturbances

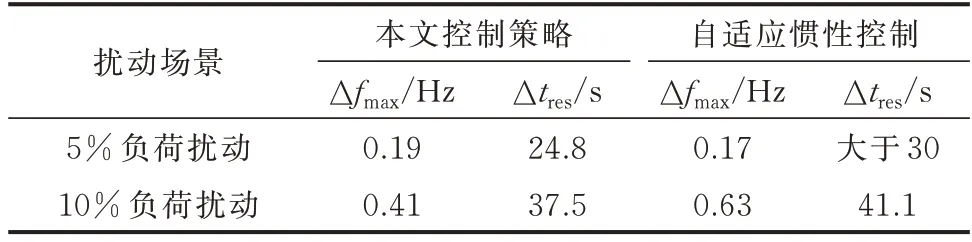
表2 调频效果对比Table 2 Comparison of frequency regulation effect

5 结语

本文提出了基于ROCOF 的风电机组一次调频控制策略，使风电机组实现不同功率不平衡量下基于ROCOF 分段区间的频率自适应控制。经理论研究和仿真分析得到如下结论:

1）根据功率不平衡量与ROCOF 的线性关系，可根据本地频率测量估计初始ROCOF，从而反映功率不平衡量大小。相较于频率偏差信号作为控制策略的触发信号，ROCOF 对扰动检测更具超前性。

2）综合惯性控制能根据频率自发调节功率增量，可对功率波动场景进行自适应频率调节。提出适用于较大扰动场景下的基于ROCOF 的短时功率增发控制，通过测量ROCOF 初值预估调频需求，确定瞬时增发功率，同时采用增发功率线性下降阶段缓解频率二次跌落；在风电场层通过集中控制，按照初始旋转动能裕度进行功率分配，使功率缺额主要由降载风电机组和高风速风电机组承担，提高一次调频能力。将上述两种控制策略结合，能有效提高风电场参与调频的能力。

后续研究工作中，将根据电网频率的时空分布特性，分析本地初始ROCOF、惯量和不平衡功率的关系，同时考虑实际系统确定临界功率不平衡量，从而合理设定ROCOF 阈值。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。