基于鲁棒多标签生成对抗的风电场日前出力区间预测

潘 霄，张明理，刘德宝，赵 琳

（1. 国网辽宁省电力有限公司经济技术研究院,辽宁省沈阳市 110015；2. 国网辽宁省电力有限公司超高压分公司,辽宁省沈阳市 110003）

0 引言

近年来,风电等可再生能源越来越受到重视,但风电出力的强随机性与波动性给电力系统的安全稳定运行带来了困扰。为了优化电网调度,提高风电场效率,准确的风电功率预测极其重要［1］。

以数值天气预报（numerical weather prediction,NWP）为基础的物理法已成功应用于风电预测领域［2-4］。文献［5］将变分模式分解与权值共享门控循环单元结合形成新的预测模型,该模型能够更好地把握风电功率的趋势,具有更好的预测精度。文献［6］提出一种优选状态数的马尔可夫链蒙特卡洛法,解决了传统马尔可夫链蒙特卡洛法应用于风电功率序列建模时难以较好地同时模拟原始风电功率序列的概率分布特性和自相关特性的问题。文献［7］考虑了NWP 的风速偏差修正以及相邻风电场地理位置之间的风速相关性,提出了一种基于高斯过程的组合加权风电功率预测模型。文献［8］分析了采用物理预测方法可能导致预测误差的环节,提出了误差源分析方法,提高了风电功率短期预测精度。文献［9］基于在线模型选择和翘曲高斯过程（warped Gaussian process,WGP）,允许在线更新WGP 基础模型,在实时风电功率预测方面取得了较大进步。上述风电功率预测方法均取得了较好的预测效果,但也存在较明显的缺点,如需额外的背景信息,建立预测模型较困难［10］等。

与物理法不同,采用数据驱动的风电功率预测方法强调从多源、多维、多模态数据中找寻其内在规律,以数据挖掘手段和人工智能算法建立输入与目标之间的映射关系［11-12］。该方法便于使用并可有效节省时间,其目的是挖掘历史数据之间的关系,建立预测模型,如小波分析法［13］、卡尔曼滤波法［14］、时间序列法［15］、神经网络法［16］以及支持向量机［17］等。文献［18］基于历史风速修正的卡尔曼滤波法对风速进行了多步修正,并通过修正后的风速进行多步功率预测。文献［19］从多源、多维、多模态的风电数据中挖掘风能、风电的因果关联,提出了一种基于数据驱动的混合深度学习模型。文献［20］提出了先提取空间特征、后捕捉时间依赖的两阶段风电功率预测建模方法。本文提出的预测方法兼顾影响风电功率的复杂多维特征,以数据挖掘和人工智能算法挖掘待预测日风电功率与其特征之间的隐含关系,是一种有效的区间预测方法。

本文为提高日前风电功率区间预测的准确性和稳定性,提出了一种基于鲁棒多标签对抗生成的风电场日前出力区间预测方法。首先,分析影响风电出力的因素,构建包含待预测日风电功率数据及其特征的原始数据集。然后,规定原始数据集去除待预测日风电功率后的数据集为聚类数据集,将聚类数据集聚类得到带标签数据集。之后,采用受噪声影响小的鲁棒性辅助分类生成对抗网络（robust auxiliary classifier generative adversarial network,RAC-GAN）生成带标签的海量场景。最后,根据已知历史风电功率以及NWP 获得的气象特征,判别待预测日所属的簇标签类别,并在该簇标签下的生成场景中筛选相似场景集,进而获得风电功率的日前区间预测结果。

1 风电预测原始数据集构建

1.1 数据概述

采用中国东北某地区风电场2016 年整年的实际风电数据开展实验,数据的时间颗粒度为1 h。数据包含风电功率、实际的气象因素以及NWP 提供的气象信息,气象信息包括各时段的风速、风向、温度、湿度和压强。

1.2 数据分析

风电功率受风速、风向、温度、湿度、压强以及历史风电功率影响。 皮尔逊相关系数（Pearson correlation coefficient,PCC）能够分析出微小的局部形态差异,无须对风电功率数据进行归一化,能够较好地分析风电功率与各类特征间的相似性。PCC的计算公式为:

式中:x和yi分别为待预测日风电功率数据及其特征i的 数 据；xk和yik分 别 为x和yi中 的 第k个 数 据；和分别为x和yi的 数据均值；n为 数据总数。

参考现有风电功率预测文献［5,7］,选取风速、风向、温度、湿度、压强作为初选特征；考虑到待预测日风电功率受历史风电功率影响,基于相关性分析理论［21］,分析各个历史日与待预测日风电功率之间的相关性,分别选取5 类历史日内的风电功率作为初选特征。规定待预测日t时刻风电功率的特征1 到10 分别为待预测日t时刻的风速、风向、温度、湿度、压强、历史第1 日t时刻的风电功率、历史第2 日t时刻的风电功率、历史第3 日t时刻的风电功率、历史第4 日t时刻的风电功率、历史第5 日t时刻的风电功率。待预测日风电功率时间序列与各类特征时间序列间的PCC 如图1 所示。

图1 风电功率与各特征的相关性Fig.1 Correlation between wind power and various characteristics

基于文献［21］,通过|IPCC(x,yi)|的取值范围可判断变量的相关强度:[0,0.2)代表极弱相关或无相关；［0.2,0.4）代表弱相关；［0.4,0.6）代表中等程度相关；［0.6,0.8）代表强相关；［0.8,1.0］代表极强相关。当IPCC(x,yi)为正时代表正相关,当IPCC(x,yi)为负时代表负相关。因风电出力波动性很强,影响其出力因素较多,为了保证风电功率预测的准确性,去除极弱相关及无相关的特征（图1 中蓝色线条）外,其余特征（图1 中红色线条）均用于风电预测,含风速、风向、温度、压强、历史第1 日的风电功率以及历史第2 日的风电功率共6 类特征,其中温度、压强与待预测日风电功率之间的相关性为负相关,其余特征与待预测日风电功率之间的相关性为正相关。

1.3 原始数据集构建

基于1.2 节所确定的6 类特征,将数据集预计对应的特征进行归一化处理,可得到5 类归一化特征以及2 类三角函数化特征。按照待预测日风速、风向sin 值、风向cos 值、温度、压强,历史第1 日风电功率、历史第2 日风电功率、待预测日风电功率的顺序,依次将各类特征与待预测日数据整合为一行包含24×8 个数据点的原始数据。将一年365 日数据构建为363 个原始数据样本,随机选取250 个原始数据构成原始数据集,剩余113 个原始数据作为测试集,样本格式如图2 所示。

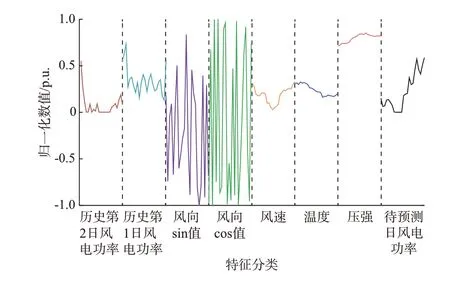
图2 原始数据集格式Fig.2 Format of original data set

2 基于RAC-GAN 的多标签风电场景生成

2.1 聚类构建多簇标签数据集

原始数据集中含有多类气象条件及历史日风电功率等多类特征,不同场景之间的差异较大。为实现风电功率精准预测,将影响待预测日风电功率的特征聚类,得到多簇标签并将原始数据集中的每个场景赋予标签,便于在预测时基于NWP 气象特征及历史日风电功率,有针对性地在对应簇标签生成场景内筛选相似场景,提高风电功率预测准确性。

k-means 聚类算法具有对大数据集处理简单、运算速度快的优势,基于该算法可实现聚类后的类与类之间特征区别明显,聚类效果更佳。k-means 聚类算法将n个数据对象聚类为k类,使每类中的数据对象相似度最高,不断重复这一过程直到划分完成,其算法步骤如下:1）确定聚类数k,并在数据中任意选取k个初始聚类中心；2）计算所有数据点到聚类中心的距离,并根据距离最小原则将数据归类于所属类别中；3）根据各类的特点,利用均值法迭代更新各类的中心值至迭代结束。

采用k-means 聚类算法分析所有特征,将聚类数据集划分为不同类别下的场景,得到带簇标签的带标签数据集。为了确定聚类类别个数,分析数据集在不同聚类类别数下的Calinski-Harabasz（CH）指标,CH 值越大代表类自身越紧密,类与类之间越分散,即聚类结果最优［22］,不同聚类数的CH 指标如附录A 图A1 所示。根据图A1 可知,最佳聚类数为6,此6 类簇代表6 种典型来风过程。将原始数据集按不同类别数赋予标签,可得到含不同标签的原始数据集。聚类后的各类原始场景集见图A2。

2.2 RAC-GAN

为解决NWP 误差对风电预测的影响,以及有限训练样本数据对风电预测准确率的影响,提出采用改进RAC-GAN 生成海量带标签的风电功率及其特征的样本。

在NWP 与实际气象存在误差的复杂场景下,即在含噪声的场景下,为解决影响风电出力的特征不稳定、提取难度大、风电预测准确率不足的问题,满足NWP 误差影响下多标签强鲁棒性场景生成需求,提出如图3 所示的RAC-GAN 模型。图中:DP表 示Dropout 层；TC 表 示 反 卷 积 层；FC 表 示 全 连接层。

图3 RAC-GAN 模型Fig.3 RAC-GAN model

辅助分类生成对抗网络（auxiliary classifier generative adversarial network,AC-GAN）可在生成对抗网络的基础上加入随机噪声信号标签和多分类功能,能根据标签生成指定类型样本［23］。在ACGAN 的生成器G中加入随机噪声信号z及生成样本对应标签c,生成器针对性地生成对应类别样本Xfake=G(c,z)。判别器D输出的样本X来源于真实样本Xreal以及生成样本Xfake的概率P(S|X)和属于不同类别的概率P(C|X),即

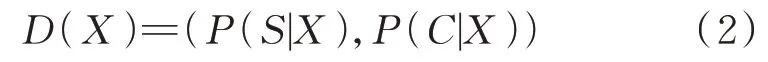
式中:P(·)为求概率函数；S为样本来源,其有2 种可能（真 实（real）,生 成（fake））；C=c,其 中,c∈{1,2,…,M},M为样本类数。

AC-GAN 中,G的目标函数为最大化LC-LS,D的目标函数为最大化LC+LS。LS和LC的表达式分别为［24］:

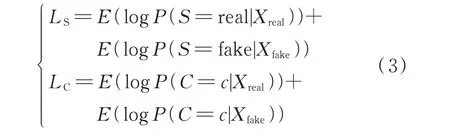
式中:E(·)为求期望函数；LS为正确源损失函数,可判别数据来源正确性；LC为正确类损失函数,可判别输出类别正确性。通过生成器与判别器内部博弈,在迭代过程中交替优化,最终提高生成器的场景生成能力。

为满足多标签的风电功率场景生成的需要,首先,在AC-GAN 的生成器输入端引入数据编码器,不直接用随机噪声信号,而使其模型根据真实风电及其特征数据预先学习浅层原始数据特征,得到随机噪声输入。然后,再输入生成器,使其针对性生成海量满足真实样本概率分布特性的生成数据,生成样本与原始样本输入判别器,判别生成样本质量,实现训练样本数据扩充。RAC-GAN 模型迭代过程中,向降低噪声影响的方向开展博弈优化,最终实现噪声干扰下多标签的鲁棒性场景生成。

2.3 基于RAC-GAN 的多标签风电数据场景生成

基于RAC-GAN 场景生成模型,输入250 个含标签样本,生成2 万个样本,原始样本与生成样本的概率密度函数（probability density function,PDF）见附录A 图A3。由图A3 可知,生成样本与原始样本的PDF 相似,验证了本文基于RAC-GAN 场景生成的有效性,场景生成可实现样本数据的有效扩容,为后文的风电功率区间预测提供数据支撑。

3 基于分标签筛选的风电功率区间预测

生成样本包含7 类影响待预测日风电功率的特征及待预测日风电功率,基于NWP 可获得待预测日的5 类气象因素特征,分别为风速sin 值、风速cos值、风向、温度、压强,且历史第1 日与第2 日风电功率已知,因此影响待预测日风电功率的7 类特征均已知。判别特征归属于哪类簇标签,基于加权PCC理论,在该类簇标签生成场景中筛选与已知特征相似度高的多个场景组成相似场景集,通过相似场景集获得风电功率区间预测结果与点预测结果。

3.1 分标签的相似场景筛选

本文所提基于鲁棒多标签对抗生成的风电场日前出力区间预测流程如图4 所示。

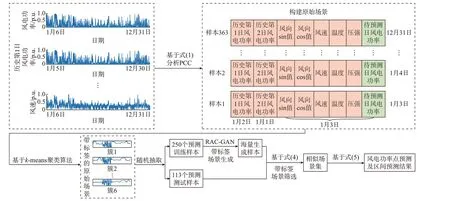
图4 风电功率区间预测流程Fig.4 Interval prediction process of wind power

不同特征与待预测日风电功率的PCC 不同,故各特征影响待预测日风电功率的程度不同。以待预测日风电功率与各特征的PCC 为权系数,规定待预测日风电功率的全部特征与第j个生成样本间对应特征的加权PCC 为IPCC,j,表达式如式（4）所示。

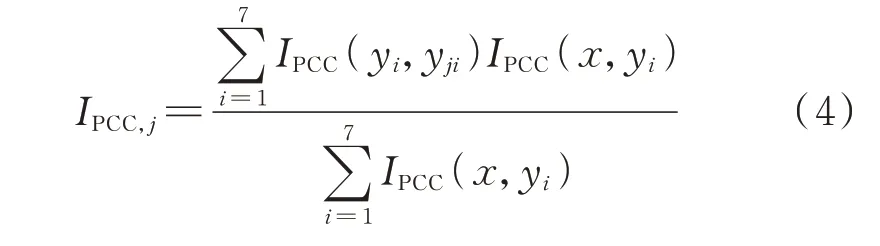
式中:IPCC(yi,yji)为已知特征i与第j个生成样本特征i之间的PCC；IPCC,j为第j个生成样本与待预测日特征间的加权PCC。

已知某一待预测日风电功率的各特征,首先基于k-means 聚类算法分析这些特征对应的簇标签,找出该簇标签所对应的生成样本；然后,根据式（4）,按照IPCC,j从大到小的顺序,在该簇标签生成样本中筛选与待预测日极强相关历史日间相似性高的N个样本,构成相似场景集,提取相似场景集合的待预测日风电功率场景并定义为矩阵Z；最后,基于Z中各时段均值与最值,得到风电功率区间预测结果与点预测结果,如式（5）所示。

式中:Pwt,max,t和Pwt,min,t分别为t时刻风电功率预测区间上、下限；Pwt,mean,t为t时刻风电功率点预测结果；a1,t为矩阵a的第1 行第t列元素,其中,矩阵a为矩阵Z中每一列的最大值组成的1×24 矩阵；b1,t为矩阵b的第1 行第t列元素,其中,矩阵b为矩阵Z中每一列的最小值组成的1×24 矩阵；c1,t为矩阵c的第1 行第t列元素,其中,矩阵c为矩阵Z中每一列的平均值组成的1×24 矩阵。

3.2 筛选样本数的确定

为确定风电功率预测所需筛选样本,采用预测区间覆盖率（prediction interval coverage proportion,PICP）、预测区间归一化平均宽度（prediction interval normalized average width,PINAW）分析不同筛选样本数下的区间预测效果,采用平均绝对百分比误差（mean absolute percentage error,MAPE）与均方根误差（root mean squared error,RMSE）分析不同筛选样本数下的点预测效果［25-26］,指标公式见附录A 表A1。筛选样本数分别设置为各簇标签所包含生成样本数的1%、2%、3%、4%、5%,得到不同筛选样本数下的预测指标,见表1。

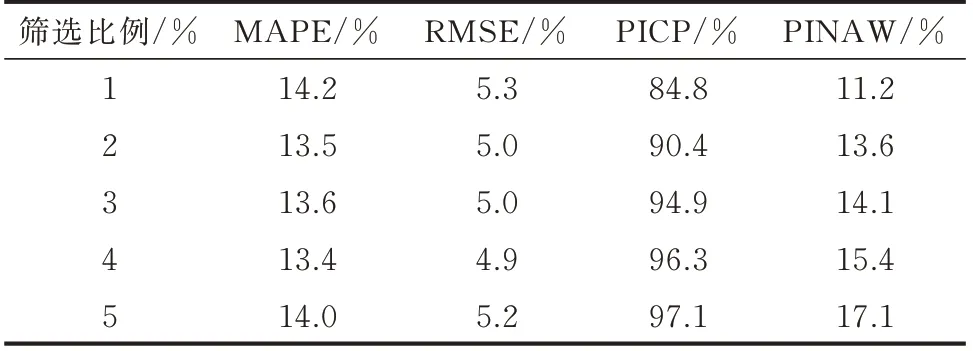
表1 不同筛选比例下的预测指标Table 1 Predictive indicators with different screening ratios

分析表1 无法直接选出最优指标的筛选比例,故规定指标在5 种筛选比例下最优时可得5 分,最差时可得1 分。按此规则,筛选比例为1%、2%、3%、4%、5%的得分依次为8、14、13、16、10,故筛选样本数为对应簇标签生成样本数的4%时的预测效果最优。

3.3 对比实验

风电功率不确定性本身是非高斯的,因此传统高斯过程不适用于风电功率预测,本文参考文献［9］,采用风电功率区间预测效果较好的WGP 开展对比实验。采用1.1 节中国东北某地区风电场2016 年整年的实际风电数据开展预测实验。在MATLAB R2015b 环境下运行,置信度分别设置为90%、95%、99%。通过在4 个季节各随机选取1 个星期数据作为预测实验的样本,得到采用不同预测方法统计预测结果的预测指标,如表2 所示。

表2 不同预测方法的预测指标Table 2 Predictive indicators of different forecasting methods

分析表2 可知,本文方法各预测指标均优于WGP 预测方法的预测指标,证明本文方法的区间预测效果好。风电功率受季节影响较大,故分别分析本文方法和不同置信度下的WGP 方法在4 个季节的风电功率预测效果,在每个季节随机选取一日进行预测,本文预测方法得到的相似场景集的待预测日风电功率见附录A 图A4,不同方法的预测结果如图5 所示。

由图5 可知,在各季节随机抽取的4 日中,本文预测方法的MAPE 与PINAW 均为最小、PICP 均为最大。这是因为先经过场景生成得到海量生成场景,通过分标签的相似场景筛选得到的相似场景与真实场景相似度高,故预测误差百分比较低、预测区间宽度较低、预测区间覆盖率较高。综上所述,在进行风电功率日前预测研究中,无论是4 个季节各选取1 个星期还是4 个季节随机选取1 日进行实验,本文方法均具有一定优势。

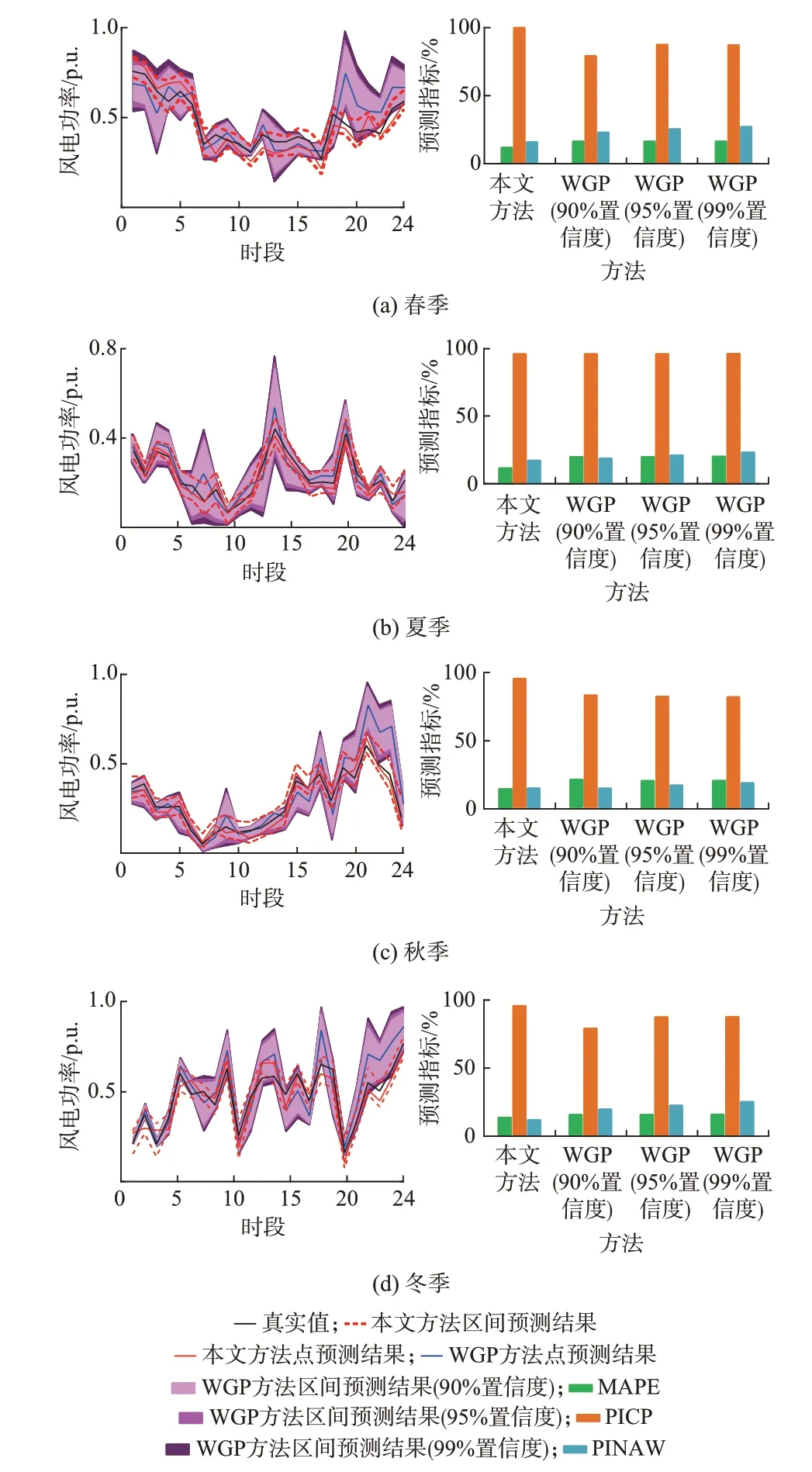
图5 各季节风电功率区间预测结果Fig.5 Interval prediction results of wind power in each season

3.4 NWP 误差影响下的预测效果分析

本文风电预测所用特征包含NWP 获得的气象特征,NWP 气象特征与真实气象之间存在误差,其误差大小会直接影响筛选相似场景的质量,进而间接影响预测效果。为了分析本文方法在不同NWP误差下的预测效果,在RAC-GAN 场景生成时加入噪声以模拟NWP 误差,并设置信噪比分别为20、25、30、35、40 dB 来模拟NWP 误差［27］。基于分标签筛选的风电功率区间预测方法,获得不同信噪比下的区间预测指标如表3 所示。

分析表3 可知,信噪比越小,噪声越强,即NWP误差越大,越不利于预测结果的准确性与稳定性,即20 dB 时预测效果最差,此时本文方法预测指标也优于WGP 预测方法,证明本文预测方法在存在较大NWP 误差时依然能够保证区间预测的良好效果,证明了本文基于RAC-GAN 场景生成的风电功率区间预测方法的实用性。

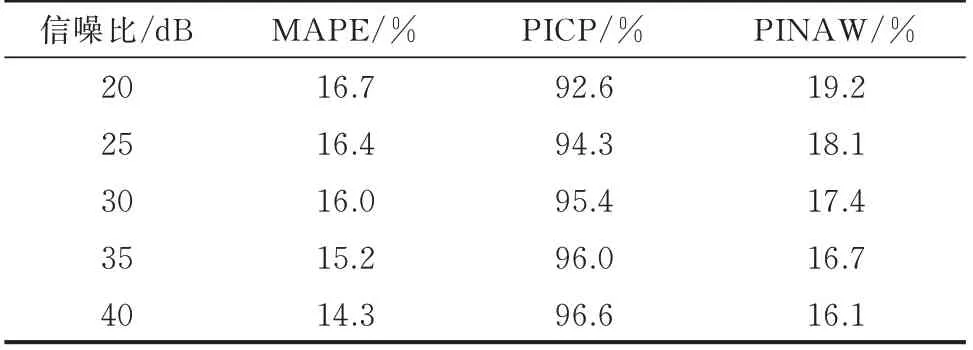
表3 不同信噪比下的预测指标Table 3 Predictive indicators with different signal-to-noise ratios

4 结语

为实现风电功率的日前区间预测并保证其准确性,保证电网运行的可靠性与经济性,提出一种基于鲁棒多标签对抗生成的风电场日前出力区间预测方法。主要结论如下:

1）根据已知待预测日风电功率的特征可确定待预测日的簇标签类别,在该类簇标签下筛选出与其特征相似度高的场景,进而获得风电功率点预测及区间预测结果,提高了风电功率的点预测与区间预测精度,与传统WGP 区间预测方法相比,验证了本文预测方法的有效性。

2）考虑NWP 与实际气象条件之间存在差异性,在构建基于RAC-GAN 的场景生成模型时考虑加入噪声模拟NWP 误差,在此条件下得到预测结果。经过仿真验证,NWP 误差会略微降低预测结果准确性与可靠性,但计及NWP 误差的方法仍比WGP 方法预测效果好,验证了本文方法承受NWP误差的能力更强,预测结果受外界因素干扰小。

本文基于多标签场景生成理论,提出了一种风电功率区间预测方法,预测方法兼顾影响风电功率的复杂多维特征,以改进RAC-GAN 挖掘待预测日风电功率与其特征之间的隐含关系,提高了区间预测的精度。但本文采用数据集的采样时间间隔为1 h,还不够精确,后续研究工作将尝试采用时间间隔更精确的数据集；本文采用未限电的风电场出力数据,未考虑调度限电或控制等因素的影响,后续研究将采用限电的数据集,考虑限电对历史数据的影响。